模糊時間窗下多船型不定期船調度與航速聯合優化
范厚明, 于佳琪, 馬夢知, 蔣曉丹, 慈吉利, 翟志偉
(1.大連海事大學 交通運輸工程學院,遼寧 大連 116026;2.大連海事大學 戰略管理與系統規劃研究所, 遼寧 大連 116026;3.中遠海運散貨運輸有限公司,廣州 510220;4.香港明華船務有限公司, 香港特別行政區 999077)
燃油成本是船舶營運的主要成本,由于燃油消耗與航速之間存在非線性關系,航速的調節會引起燃油成本的大幅波動,而船公司為確保貨物在規定的時間內被運送到目的地,需要優化配置船舶及其航速,以滿足貨主需要的同時獲得更好的經濟效益,因此,船舶調度與航速優化一直是船公司關注的問題.
近年來,學者們對不定期船調度問題與航速優化問題進行了深入探索.針對不定期船調度問題,Jetlund等[1]建立非線性整數規劃模型,運用啟發式分解方法解決多艙位化學品船調度問題.Fagerholt[2]研究軟時間窗下不定期船調度問題,目標函數中加入違反時間窗所產生的懲罰成本.Br?nmo等[3]提出了一個多起始局部搜索算法解決不定期船調度問題,此算法能夠在合理時間內為船公司的不定期船調度提供最優或接近最優方案.Korsvik等[4]將禁忌搜索啟發式算法運用到船公司決策支持系統,為多家船公司不定期船調度提供科學決策.Fagerholt等[5]在模型中考慮了貨物之間耦合性因素,以船公司獲得最大利潤為目標建立數學模型,設計了禁忌搜索算法解決工程船舶調度問題.Hemmati等[6]采用自適應鄰域搜索算法求解不定期船舶與庫存路徑相結合問題.Armas等[7]考慮貨物裝貨港與卸貨港時間窗約束,建立離散時間窗船舶調度模型,采取貪婪隨機自適應搜索與變鄰域相結合算法解決帶時間窗的不定期船調度問題.
針對不定期船調度拓展問題,Korsvik等[8]和Br?nmo等[9]為了解決貨量可變不定期船調度問題,分別運用了禁忌搜索算法和列生成算法確定貨物實際裝載量及船舶調度計劃.Meng等[10]將燃油補給納入到船舶調度問題中,建立了船舶調度與燃油補給聯合優化模型.鑒于船舶調度、航線優化、航線配船有很強關聯性,Lin等[11]建立了一個三方面問題聯合優化的不定期船調度數學模型.由于不定期船舶無固定航線與船期表,在實際情況中不定期船舶裝卸貨時間晚于貨主期望時間是常有的情況,但是超出貨主期望時間窗送達貨物將會造成貨主資金損失或產生過高庫存成本,所以如何平衡貨主滿意度與最大限度控制航運企業成本是一個亟需解決的實際問題,直接關系到船公司在整個不定期船運輸市場上的競爭力.為解決此問題,Yu等[12]建立貨主滿意度最大化和承運人運營成本最小化雙目標模型,通過模糊關系函數體現貨主滿意度,利用非支配排序遺傳算法(Non-dominated Sorting Genetic Algorithm,NSGAII)求解該問題,但此研究僅以既定船舶的單航次運輸任務為研究對象.Thai等[13]建立了一個衡量不定期船舶服務質量的模型,可將其應用于客戶對船公司進行服務質量評估.Lee等[14]針對班輪運輸分析慢速航行與燃油消耗、航行時間、運輸貨物可靠性之間的關系.Mallidis等[15]提出了一種分析建模方法,用于量化慢速航行對承運人的航次成本和托運人總成本的影響,證明了隨著船舶航次接近結束,慢速航行和速度調整策略對托運人的總成本的影響趨于增加.
部分學者在航線確定情況下,對航速優化展開研究.Norstad等[16]和Hvattum等[17]分別提出多起點搜索算法與精確算法求解固定航線上每一艘船舶最優航速.Harilaos等[18]分析燃油價格、運費率、貨物庫存成本、裝貨量4個因素對航速優化與成本所產生的影響,為航運企業經濟效益與改善環境提出合理建議.Fagerholt等[19]從節能減排的角度出發,以追求整個航次的燃油消耗量最少為目標,建立了船舶航速優化數學模型,并提出了到達時間離散化的啟發式算法對模型進行求解.唐磊等[20]建立帶時間窗的不定期船航線規劃模型,設計了求解最優航速的遞歸平滑算法.殷翔宇等[21]采用了控制變量法分別研究燃油價格及不同船舶固定成本的變化對不定期船舶航次日均盈利額的影響.李錚等[22]解決航線不變情況下,不定期船舶運輸的航速優化問題.航速大小決定了船舶到達港口時間,從而影響貨物選擇和船舶調度計劃,因此船舶調度與航速優化是相關聯問題,部分學者對此進行聯合優化.Wen等[23]分別以最短航行時間、總成本最小、碳排放量最少為目標函數得出不同目標函數下船舶調度計劃與最優航速.Wen等[24]進一步細分了壓載航程與載貨航程的燃油消耗,考慮各地油價的差異性,運用分支定價和啟發式列生成算法求解航速可變不定期船調度問題,但模型僅考慮航行成本,未考慮港口成本等現實因素.唐磊等[25]將航速對航次成本、航次時間的影響納入到研究中,提出了不定期船調度的非線性網絡規劃模型,設計了基于集合劃分方法的兩階段算法求解.但在假設中認為合同貨物只要在規劃期內運到即可,沒有嚴格的裝卸時間窗約束,并且在實例中未考慮租船運輸貨物情況.俞超等[26]認為在航運合約中速遣費、滯期費對港口選擇有重要影響,因此加入速遣費、滯期費和貨主存在違約等約束,利用兩階段粒子群算法,解決不定期船舶航速優化和港口選擇問題;并指出在未來的研究中,可以考慮多船舶、多時期情況下的船舶調度和航速優化問題.李曉君等[27]研究不定期船舶中半潛船航速問題,在進行航速優化的同時考慮了貨物分配問題,采取插入法與改進的遞歸平滑算法求解該問題.
通過對上述文獻研究成果的梳理發現,現有研究多對不定期船調度與航速優化分別進行研究;少數船舶調度與航速聯合優化的文獻中只考慮了船公司經濟效益,而忽視了貨主滿意度對船公司船舶調度計劃的影響.同時,在實際情況中,為了不影響船公司信譽以及增加自身經濟效益,對于自有船舶無法運輸的貨物,船公司可以采取租船方式進行運輸,現有文獻的模型較少包含租船方式運輸貨物的情況.針對以上問題,本文考慮貨主滿意度,船舶裝載量對于燃油消耗的差異性以及船舶配置情況等實際因素,對多船型不定期船調度與航速進行聯合優化,以增加船公司經濟效益,提高運輸可靠性,為不定期船調度方案的制定提供決策支持.
1 問題描述及模型建立
1.1 問題描述
在不定期船調度問題中,假設有n票貨物,編號為i,貨物i對應的裝貨港和卸貨港在運輸網絡中分別用節點i和節點n+i表示.NP={1,2,…,n}是貨物裝貨節點集合,ND={n+1,n+2,…,2n}是貨物卸貨節點集合,不同的節點可以對應同一個地理位置相同的港口.本文所研究的不定期船調度問題可以定義在一個(NP∪ND,A)運輸網絡上,其中A={(i,j):i,j∈NP∪ND,i≠j}.船隊中可用船舶集合為K={1,2,…,k,…,φ}.在硬時間窗航速不變情況下船舶調度計劃安排如圖1所示,圖中第3票與第4票貨物由于自有船舶無法在貨主期望時間內開始服務,只能由即期市場上的程租船3、4運輸.
由于航速決定燃油成本的高低和航行時間的長短,通過調整航速,船舶2從港口6到港口7的航行時間(T)由原來的6 d變為4 d,因此船舶2可以及時到達第4票貨物的裝貨港,如圖2所示.同時,在實際情況中,由于航線距離長,海上不確定因素多,船舶晚于貨主期望時間到達港口是常有情況.當貨主放寬對貨物裝卸時間窗要求,在模糊時間窗下,船舶1可以在貨主可容忍的服務時間范圍內對第3票貨物進行服務.此時船舶調度計劃可以減少使用兩艘程租船舶.因此本文從船公司角度出發,不僅注重通過優化航速提升船公司營運收益,而且兼顧貨主滿意度對船舶調度計劃的影響,全面考慮貨物、港口、航線、多船型對成本、運費收入等經濟參數的影響,研究船舶在給定運輸網絡上的最佳調配使用問題.主要決策涉及制定船舶調度方案,計算最佳航速和船舶配置情況.
1.2 基本假設
為便于建立模型,參考文獻[11,24]做出以下假設:
(1) 假設船公司擁有多種船型,每一種船型對應船舶載重量、航速、吃水等參數均不相同;
(2) 船舶每次只能運輸一票貨物,中間不能加裝其他貨物,對于待運輸貨物允許船公司選擇自有船舶運輸或在即期市場上通過租船方式運輸;
(3) 提前可以確定每一票貨物的裝貨港、卸貨港,裝卸貨時間要求等相關信息;
(4) 船舶從任意港口或者航行中某個位置出發,按照所承運的貨物裝貨港來確定初始位置,并且完成一個航次后不必返回初始港口;
(5) 假設燃油價格不隨時間變化.
1.3 符號說明
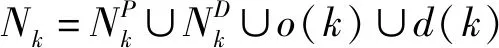
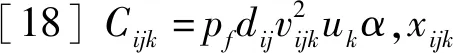
1.4 模糊時間窗與貨主滿意度
對于模糊時間窗下船舶調度問題,船舶在港口開始服務時間與貨主滿意度、時間成本有直接關系.由于船東過早將貨物卸至堆場,貨主無法及時組織運力進行提貨,因此需要承擔貨物在碼頭的堆存費用,并且由于不定期船主要運輸大宗散貨糧食等,未按照貨主期望時間送達將產生貨損,對貨主造成收益損失,降低貨主滿意度及船公司信譽度.采用模糊時間窗可以較好刻畫貨主滿意度與時間關系.當船舶k在港口i期望時間窗[ETi,LTi]內進行服務時,貨主滿意度為最高值1,且沒有時間成本;當船舶k在港口i期望時間窗外,但在模糊時間窗內進行服務時,貨主滿意度隨著偏離貨主的期望時間窗的加長呈下降趨勢,而時間成本呈上升趨勢;當船舶k在時間窗EETi和ELTi處服務時,貨主的滿意度為最低值0,且時間成本達到最高值;當船舶k超出模糊時間窗[EETi,ETi,LTi,ELTi]到達港口i時,則貨主不接受此票貨物.
本文假設時間成本的最高值為Ct,S(Tik)是在Tik時刻船舶k在港口i準備接受服務時貨主的滿意度,Ct(Tik)是船舶k在Tik時刻在港口i準備接受服務所產生的時間成本.貨主滿意度S(Tik)和時間成本Ct(Tik)的變化趨勢如圖3~4所示.根據實際情況,可看出貨主對于船舶過早將貨物送達的容忍度將高于船舶晚于貨主期望時間的容忍度,因此在[EETi,ETi]時間段內貨主滿意度與時間線性關系斜率大于在[LTi,ELTi]時間段.
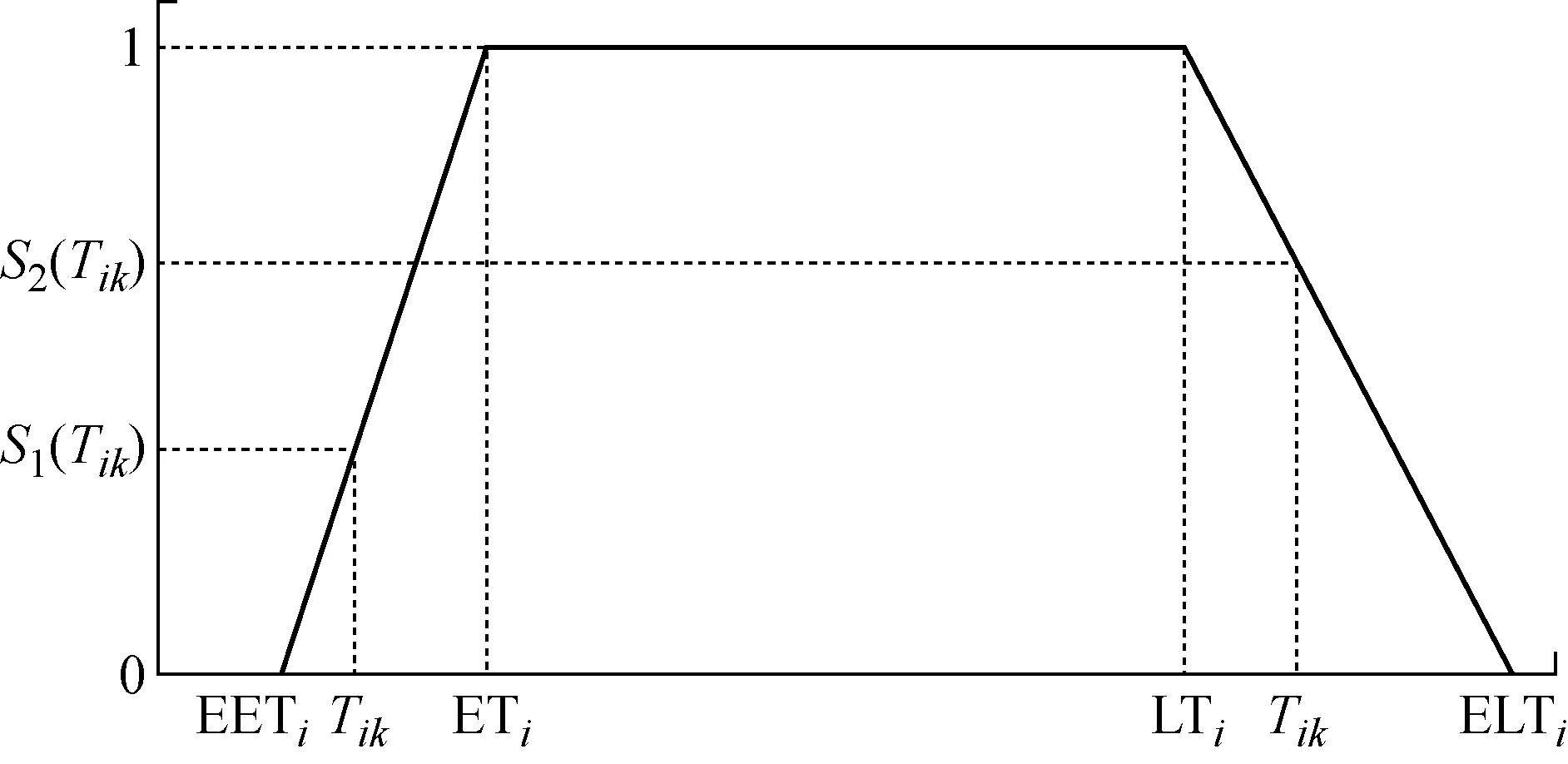
圖3 貨主滿意度變化趨勢Fig.3 Variation in shipper satisfaction
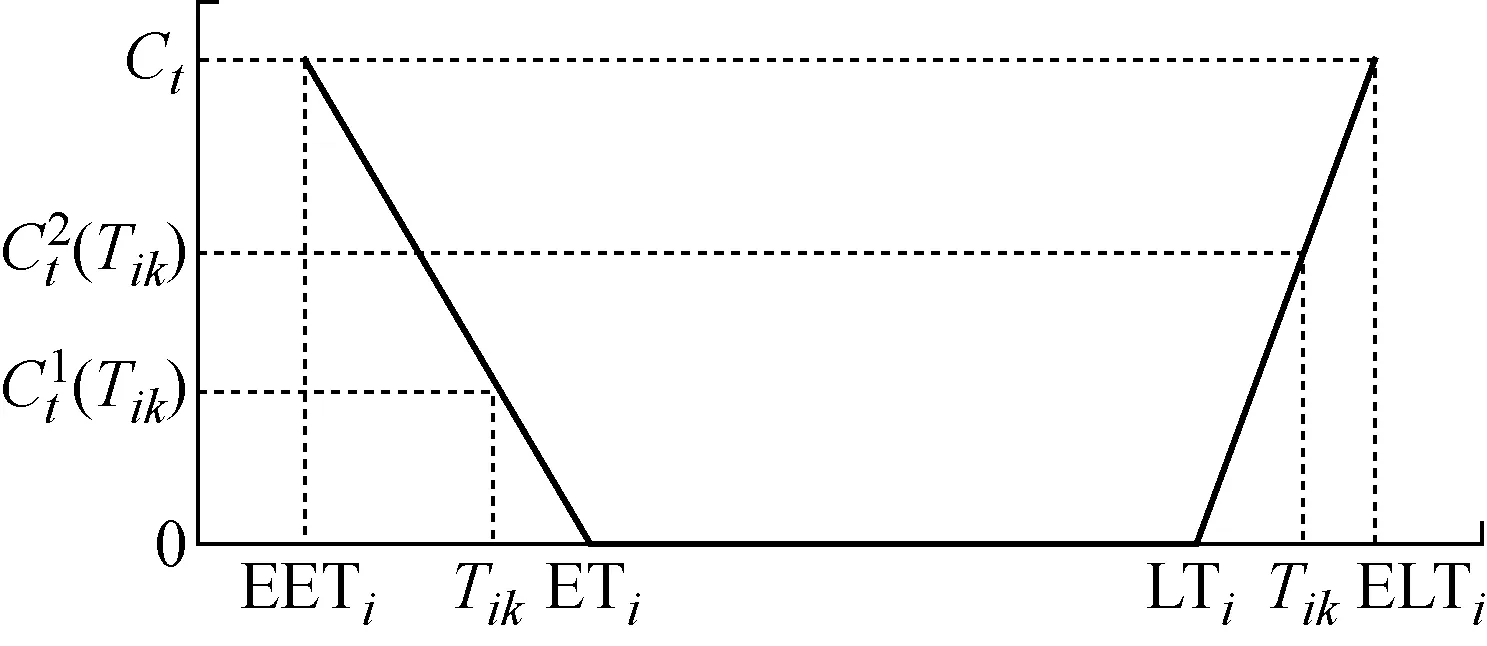
圖4 時間成本變化趨勢Fig.4 Variation in time cost
其中,貨主滿意度S(Tik)和時間成本Ct(Tik)的計算公式如下:
(1)
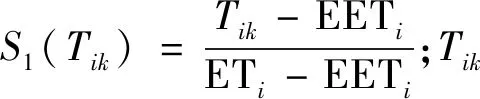
Ct(Tik)=
(2)
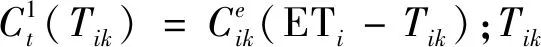
1.5 模型建立
模糊時間窗下多船型不定期船調度與航速聯合優化模型如下:
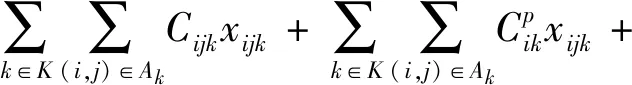
(3)
(4)
(5)
?k∈K,i∈Nk/{o(k),d(k)}
(6)
(7)
(8)
(9)
(10)
Tik∨EETi+tik+di(n+i)/vi(n+i)k=T(n+i)k
?k∈K,(i,j)∈Ak
(11)
xijk(Tik∨EETi+tik+dij/vijk)=Tjk
?k∈K,(i,j)∈Ak
(12)
Tjk≤ELTj?k∈K,j∈Nk
(13)
xi(n+i)kw(n+i)k=0
(14)
x(n+i)jk(qj-wjk)=0
(15)
0≤wik≤Qk?k∈K,i∈Nk
(16)
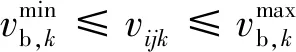
(17)
(18)
Yi∈{0,1} ?i∈NP
(19)
xijk∈{0,1} ?k∈K,(i,j)∈Ak
(20)
式(3)表示模型的目標是規劃期內船公司總成本最小化,包括5部分,第1部分為航行成本,第2部分為港口成本:包括港口使費及在港停泊費用,第3、第4部分為超出貨主期望時間產生的等待與懲罰成本,兩部分共同構成了時間成本,第5部分為通過租船方式運輸貨物所產生的租船成本;式(4)表示船舶僅一次從初始位置出發;式(5)表示船舶僅一次到達運輸最后一票貨物的卸貨港;式(6)表示到達與離開任意港口的船舶數量相同;式(7)表示對于待運輸的貨物可以選擇自有船舶運輸或者從即期市場上租船運輸;式(8)保證船舶的調度計劃在掛靠同一貨物的裝貨港和卸貨港上保持一致;式(9)、式(10)分別表示船舶不能連續掛靠兩個裝貨港和兩個卸貨港,即船舶運輸一票貨物途中不能加裝其他貨物;式(11)、式(12)分別表示船舶從貨物裝貨港到卸貨港的時刻和船舶航行線路與航行時間的一致性,∨表示兩者之間取最大值;式(13)表示船舶k服務完港口i后到達港口j的時刻不超過最晚開始服務時刻;式(14)、式(15)表示船舶航行線路與船舶載貨量之間的關系;式(16)表示船舶運輸每一票貨物的貨量不能超過船舶最大載重量;式(17)、式(18)分別表示船舶壓載和載貨航行速度可取的范圍;式(19)和式(20)表示變量約束.
2 模型求解
模糊時間窗下不定期船調度與航速聯合優化模型是一個非線性規劃模型,結構與成分較為復雜,同時含有0-1變量、連續變量以及等式、不等式混合.針對模型的結構特征本文設計了變鄰域遺傳模擬退火算法.遺傳算法(Genetic Algorithm,GA)是一種遵循自然界中適者生存規則和遺傳理論而產生一種全局搜索啟發式算法,但該算法存在著易早熟、容易陷入局部最優的缺點.變鄰域搜索算法(Variable Neighborhood Search,VNS)是一種通過對當前解的不同鄰域結構展開一定范圍搜索,以獲得多樣搜索策略的元啟發式算法,相對于遺傳算法來說局部搜索能力、深度搜索能力較強.模擬退火算法(Simulated Annealing,SA)是一種以概率l 收斂于全局最優解的全局優化算法,具有漸近收斂性、并行性.三者結合能夠同時進行局部搜索與全局尋優.算法流程如圖5所示.其中:Pop_best表示當前代最優個體適應度;Global_best表示全局最優個體適應度.設置以下參數:迭代次數Gen;最大迭代次數Maxgen;種群規模Popsize;自適應進化壓力系數β.
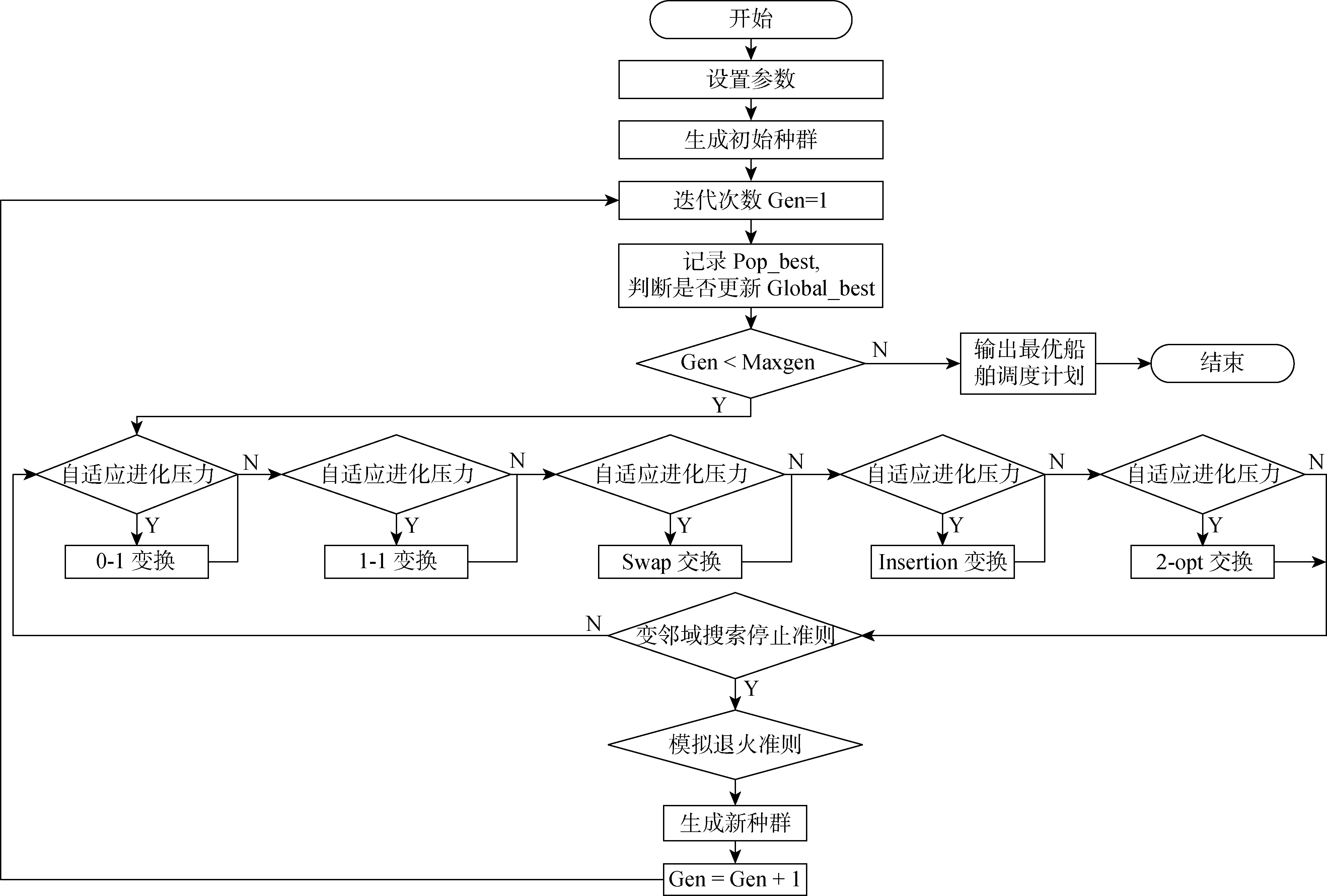
圖5 算法流程圖Fig.5 Flowchart of the proposed algorithm
2.1 編碼與初始種群的生成
算法中解方案采取實數編碼方式,染色體長度為貨物數量,染色體上基因的位置就是船舶服務貨物的順序.初始種群在船型、時間兩個雙重約束下生成.具體的方法為:首先將貨物與各船型進行匹配,得出每一艘船舶能夠運輸的貨物,構成該船舶的初始航線;再檢驗每一艘船舶的初始航線是否滿足時間約束,即船舶從初始位置出發,按照貨物對應的港口編號依次訪問,當船舶不能同時滿足貨物裝貨港、卸貨港的時間窗約束時,將此票貨物從該型船舶移除,檢驗將其插入到其他型船舶能否運輸;若該型船舶能夠運輸此票貨物,則將此貨物從其他型船舶航線中移除,不再安排船舶運輸此票貨物.例如共有3艘自有船舶,編號為1-2-3,待運輸貨物10票,1-2-4-5-3-7-9-8-6-10為10票貨物的全排列,構成一條染色體.船舶1能夠運輸貨物{5-8-9-10},船舶2能夠運輸貨物{1-2-3-5-8-9-10},船舶3能夠運輸貨物{1-2-3-4-5-6-7-8-9-10},船舶1運輸貨物9后不能滿足貨物10的時間窗約束,則船舶1航線為5-8-9;此時將船舶2和船舶3生成的初始航線中已被安排運輸的5、8、9票貨物移除,船舶2初始航線變為{1-2-3-10},船舶3初始航線為{1-2-3-4-6-7-10},再檢驗船舶2是否滿足每一票貨物裝卸港時間窗要求,都能夠滿足則生成船舶2航線{1-2-3-10};刪除船舶3初始航線中已被安排運輸貨物,檢驗船舶3航線能否滿足時間窗約束,依次類推,生成初始種群.
2.2 計算適應度
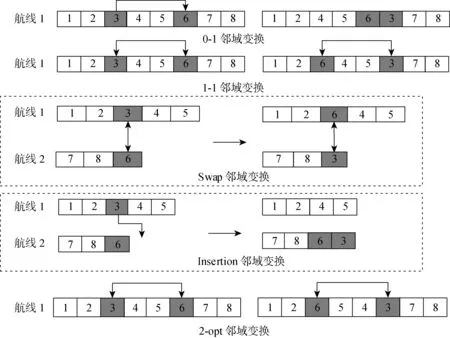
本文染色體的適應度為所有船舶的航行成本、港口成本、時間成本、租船成本之和,搜索當代種群中的最優個體適應度值,若Pop_best 圖6 變鄰域搜索策略Fig.6 Variable neighborhood search strategy (1) 0-1鄰域變換:在航線1隨機選擇第i票貨物,根據貨物裝卸港口之間的距離由近到遠排序,將此票貨物插入到航線1貨物j后面. (2) 1-1鄰域變換:在航線1上隨機選擇兩票貨物i,j,直接將兩票貨物i,j互換位置. (3) Swap鄰域變換:分別在航線1和航線2上隨機選擇兩票貨物i,j,將貨物i,j從所在航線中分離,交換航線1和航線2上兩票貨物位置. (4) Insertion鄰域變換:分別在航線1和航線2上隨機選擇兩票貨物i,j,將航線1上的貨物i移除插入到航線2貨物j后面. (5) 2-opt鄰域變換:隨機選擇航線1上的兩票貨物,將兩票貨物i,j之間的貨物進行逆序排列. 為了驗證提出的數學模型有效性,本文算例由文獻[29]提供的某船公司不定期船舶歷史運輸數據生成.該算例共有7艘自有船舶,船舶參數信息設置如表1所示,貨物為30票大宗散貨,需要整船運輸,相關貨物信息如表2所示,時間窗以小時計算.pf燃油價格為590美元/t.根據文獻[30]可知對生產性停泊,船舶停泊費費率為0.23元/(t·d);對于非生產性停泊,船舶停泊費費率為0.15元/(t·h);由于延誤產生的單位費率為0.30元/(t·h). 表1 自有船舶相關信息Tab.1 Information of self-owned ships 表2 貨物信息Tab.2 Cargo information 在進行實例計算之前,為了驗證本文設計的變鄰域遺傳模擬退火算法(Variable Neighborhood Genetic Simulated Annealing,VNGSA)的有效性,對不定期船舶小規模算例及標準算例進行測試. 3.2.1小規模算例 針對本文所建模型,生成2艘船舶3票貨物的小規模算例,其中船舶1和船舶2初始位置在ROTTERDAM 和SETUBAL港口,速度范圍為13~14 kn,貨物數據如表3所示,進行算例分析. 表3 小規模算例貨物信息Tab.3 Small scale cargo information 通過枚舉所有可能的船舶掛靠港口順序及采取的速度,計算小規模算例最優解.本算例兩艘船舶運輸3票貨物,船舶1可運輸3票、2票、1票、0票貨物,對應船舶2運輸0票、1票、2票、3票貨物,同時考慮自有船舶運輸情況,因此共有路徑方案43種.每一種方案又對應不同航段速度方案,當分別運輸3票、2票、1票貨物時,航段速度方案分別有64種、16種、4種,因此總共有 1 753 種方案.計算每一種調度方案的目標函數值,得出結果為船舶1運輸貨物2、1,船舶2運輸貨物3,總成本為 330 785 美元,與本文啟發式算法求得最優解一致,證明本文算法有效性,可求解船舶調度與航速聯合優化問題. 3.2.2標準算例 采用標準算例測試算法性能,標準算例來源于http:∥iot.ntnu.no/users/larsmahv/benchmarks/.此算例是一個求解硬時間窗下多船型不定期船調度問題,其中成本組成有船舶航行成本、貨物未被運輸所產生的成本,約束條件有港口時間窗,船舶容量等.標準算例與本文不同在于沒有航速約束以及時間成本.采用MATLAB 2016a編譯程序運行(電腦操作系統為Windows 10,運行內存為8 GB,CPU為Intel(R) Core(TM) i7-7700,主頻為3.60 GHz). 選取標準算例中小規模、中等規模、大規模算例各5組,共15組.其中C8代表8票貨物,需要掛靠16次港口,V3代表3艘船舶.每一組算例船隊中的船舶性能、初始港口位置等都有所不同.表4是本文設計的VNGSA算法與GA算法對標準算例求解結果的比較.其中:ηbest表示算例已知最優解;Z表示算法所求得最優解;ε為Z與已知最優解的計算偏差;εave表示15組算例誤差平均值.由于算法參數取決于問題規模,本文對于小規模、中等規模、大規模算例的種群規模、最大迭代次數取值不同.針對種群規模分別設置為20~100,100~500,500~1 000,最大迭代次數分別為15~150,150~300,300~800. 采用本文算法與遺傳算法計算C16_V6_3算例,設置種群規模為500,最大迭代次數為300,得到兩種算法對比收斂圖如圖7所示.根據收斂圖可以看出在同樣的種群規模與迭代次數下,本文所設計的算法與遺傳算法相比收斂速度較快,能夠較快獲得問題的最優解. 圖7 算法收斂圖對比圖Fig.7 Comparison of algorithm convergence 通過表4可以看出對于小規模和中等規模問題本文算法能夠求出與算例已知最優解相同結果.將兩種算法對比分析,GA算法求解出15組算例中7個最優解,而本文算法求解出15組算例中11個最優解,兩種算法求得結果與已知最優解的計算偏差平均值分別為2.99%、1.13%.可以看出本文算法求得結果誤差較小,這表明本文算法尋優能力較強,具有良好的求解性能. 表4 標準算例結果比較Tab.4 Comparison of standard example results 通過算法性能分析證明了本文算法有效性,因此采用此算法求解模糊時間窗下船舶調度與航速聯合優化模型.設置貨主可容忍船舶到達時間上下限為50 h,計算結果如表5所示. 表5 模糊時間窗下船舶調度與航速聯合優化Tab.5 Ship schedule and speed optimization problem with fuzzy time window 通過計算可見船隊中自有船舶沒有閑置,總共有28票貨物通過自有船舶運輸,僅剩余2票貨物需要租船運輸. 3.3.1方案有效性分析 為驗證本文方案的有效性,采用3種不同的方案對3.1算例進行計算,各方案對比分析求得結果如表6所示.方案1為硬時間窗下船公司采用固定航速制定船舶調度計劃;方案2是在方案1基礎上采用航速可變策略;方案3是基于模糊時間窗,制定航速可變的不定期船調度方案,即本文所研究的模糊時間窗下船舶調度與航速聯合優化. 表6 3種方案對比Tab.6 Comparison of three programs (萬美元) 通過表格可以看出,將方案1與方案2各項成本對比分析發現,采取航速優化能夠降低航行成本11.7%,而所花費的港口成本相近,租船成本相同,最終航速優化方案能夠降低總成本22.30 萬美元.將方案3與方案2對比,由于貨主對時間的敏感性降低,自有船舶調度計劃中可以運輸更多貨物,造成航行成本由于貨物多為自有船舶運輸而有所升高,但租船成本降低59.6%,最終總成本與方案2相比降低17.97%,與方案1相比降低21.02%.由此可見模糊時間窗下不定期船調度與航速聯合優化能夠降低航運企業成本,增加營運收益,提高貨主滿意度. 3.3.2航速策略分析 為了檢測船舶調度過程中采用不同的航速策略對航運企業經濟效益的影響.本文對船舶航行過程中最大航速、固定航速和本文的可變航速策略進行分析.其中每艘船舶固定航速平均為14.97 kn.表7為3種航速策略得到各項成本的對比. 表7 航速策略對比Tab.7 Comparison of speed strategy (萬美元) 通過表7能夠了解到航運企業若一直采用最大航速,雖然能夠通過自有船舶運輸更多的貨物,降低租船成本,但是由于高速行駛產生的航行成本比采用可變航速產生的航行成本高72.63萬美元,遠遠超過節省的租船成本,因此是各航速策略中總成本最高的一種策略.若航運企業采取固定航速,自有船舶能夠運輸的貨物與可變航速運輸貨物數量同樣多,但由于航速單一,造成航行成本及港口成本都高于可變航速下所對應的成本,最終總成本高于可變航速總成本3.86%.因此船舶在航行過程中,采取可變航速對于航運企業是一個較好的選擇,能夠壓縮成本,達到經濟效益最優. 考慮到本文的目標值主要受燃油價格、貨主滿意度的影響,以3.1算例為基礎,設計了燃油價格不同和滿意度參數變化的敏感性分析實驗,將各項成本變化進行對比. 3.4.1燃油價格敏感性分析 設置燃油價格步長100美元,共5組數據,各項成本變化趨勢如圖8所示,從圖中可以看出,隨著燃油價格的上漲,航行成本不斷增加,租船成本也隨之增加,這是由于過高的燃油成本使部分貨物通過自有船舶運輸已無法獲得較大收益,所以采用租船運輸方式.最終隨著燃油價格的不斷上漲,航運企業總成本不斷攀升. 圖8 燃油價格參數敏感性分析Fig.8 Sensitivity analysis of fuel price parameter 3.4.2貨主滿意度敏感性分析 對貨主滿意度進行分析,設置貨主滿意度以0.1的步長逐漸增長到1.0.表8給出了不同貨主滿意度下產生的航行成本,港口成本,時間成本,租船成本以及總成本. 從表8可以看出,隨著貨主滿意度升高,船舶時間成本呈遞減趨勢,在S(Tik)=0.1時,船舶時間成本最高,達到24.17萬美元,但隨之租船成本降低,貨物多由自有船舶運輸;當S(Tik)=1.0時,貨主滿意度都為最高值1.0,沒有時間成本,但總成本最高.由此說明,隨著貨主對時間要求越來越高,船公司自有船舶運輸貨物數量會有所減少,造成租船成本升高;同樣船公司總成本隨著貨主滿意度值升高而增加,若想降低船公司的總成本,則會使貨主滿意度降低;若偏注重保障貨主滿意度,則會增加航運企業成本,因此需要船公司權衡貨主滿意度與自身的經濟效益,船公司可以根據貨主對于時間的敏感性調整航速,對于需要長期合作的貨主,可以適當采取加速策略,以保證在貨主期望時間內完成貨物運輸;對于短期合作的貨主,船公司可以更加注重自身的經濟效益,采取一定策略適當延遲1-2天保證貨物送達同時船公司保持良好信譽度. 表8 貨主滿意度敏感性分析Tab.8 Sensitivity analysis of shipper satisfaction (萬美元) 本文針對不定期船調度與航速聯合優化問題,考慮貨主滿意度、自有船舶與租用船舶配置情況、航速等因素對船舶調度計劃的影響,構建了以船公司總成本最小為目標的模糊時間窗下多船型不定期船調度與航速優化模型,提出一種變鄰域遺傳模擬退火算法對其進行求解,通過算例驗證了模型和算法的有效性.結果表明:將船舶調度與航速聯合優化能夠降低航行成本;注重貨主對時間的敏感性,能夠提高貨主滿意度;所提算法先將船型與貨物匹配,再根據時間約束生成路徑,最后采用鄰域搜索策略提高求解質量;當租用船舶費用遠遠高于航行成本時,船公司可以通過提高航速增加自有船舶運輸貨物數量,減少在即期市場上租用船舶;當航行成本過高時,可以增加租用船舶運輸貨物,減少自有船舶產生的航行成本. 研究成果不僅能深化不定期船調度的理論研究,也為切實解決船公司面臨的船舶調度與航速聯合優化問題提供理論指導和決策依據.未來的研究可側重于船舶在動態環境下的實時調度問題,當出現即期貨物時,船公司考慮貨主滿意度的同時,如何配置船舶、優化航速運輸更多貨物.2.3 變鄰域搜索策略
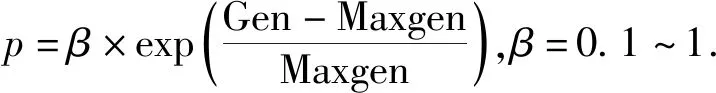
2.4 解的更新
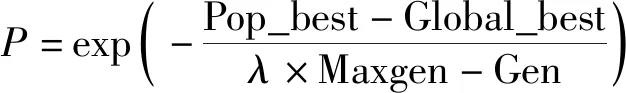
3 算例驗證及結果分析
3.1 算例描述
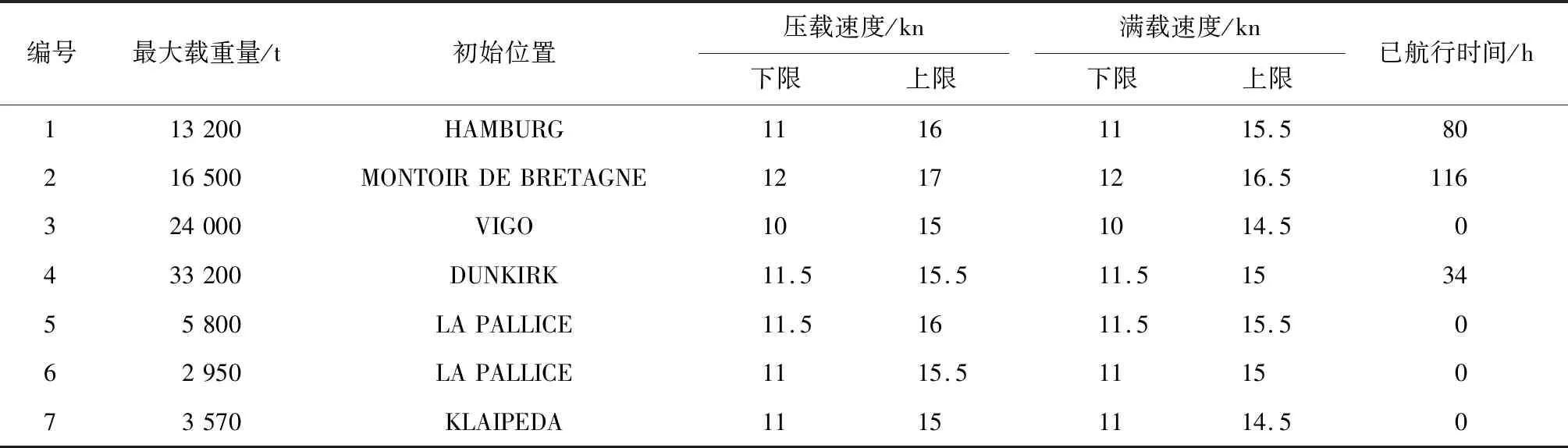
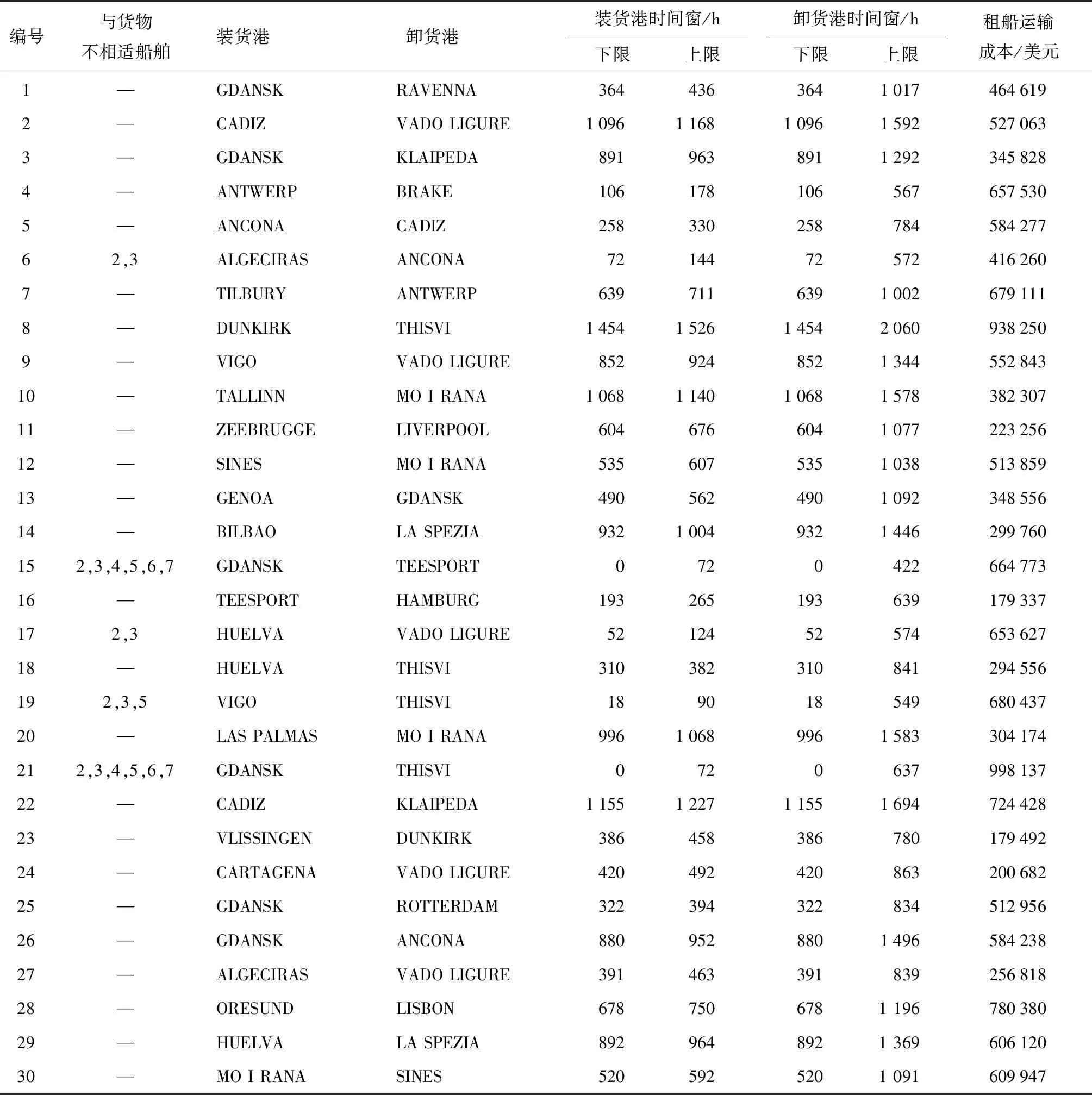
3.2 算法性能分析


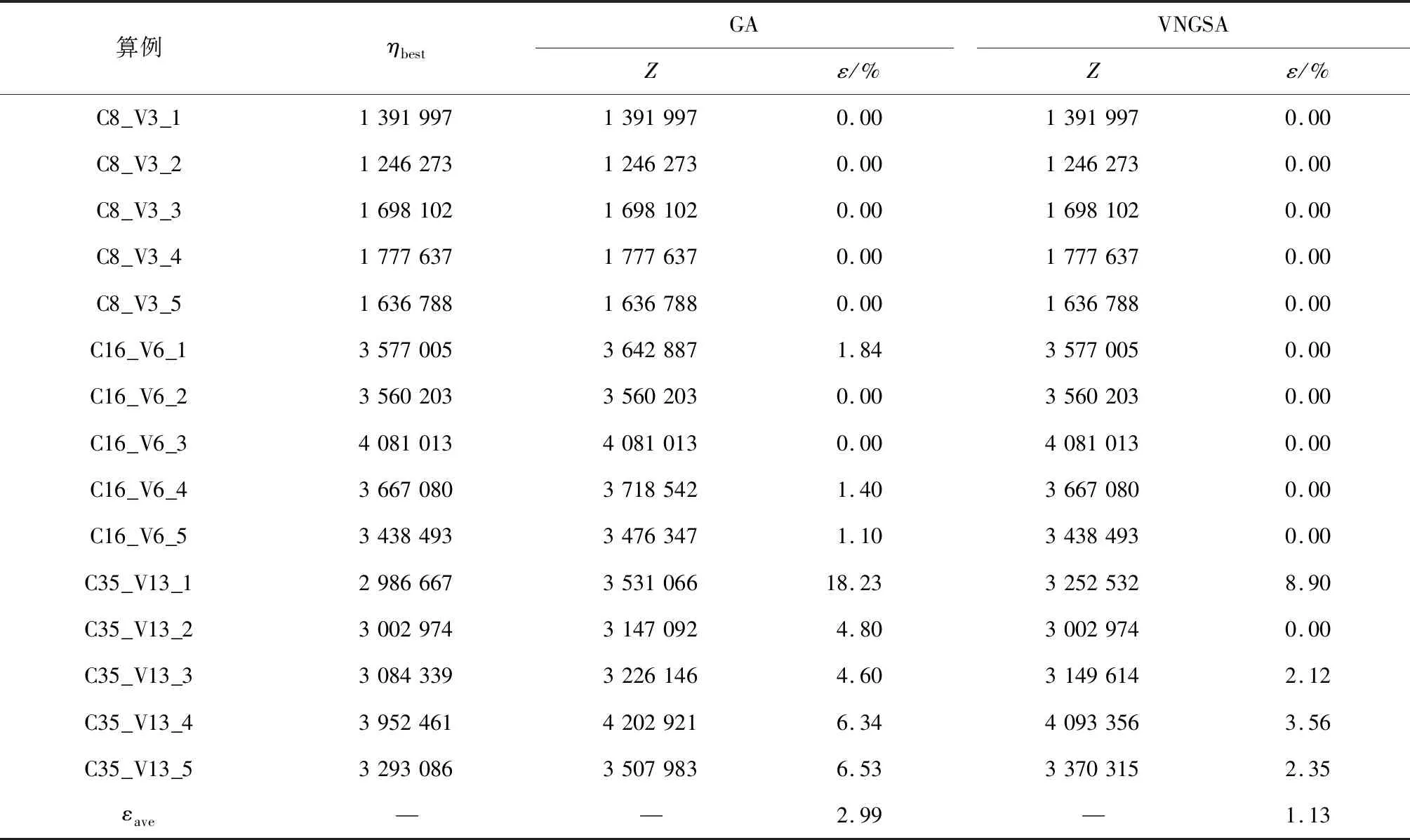
3.3 算例計算分析

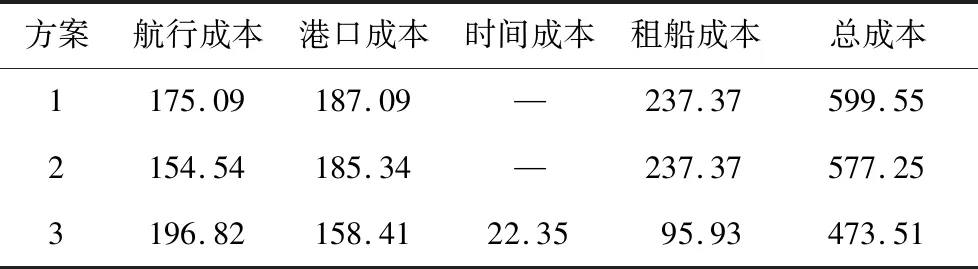
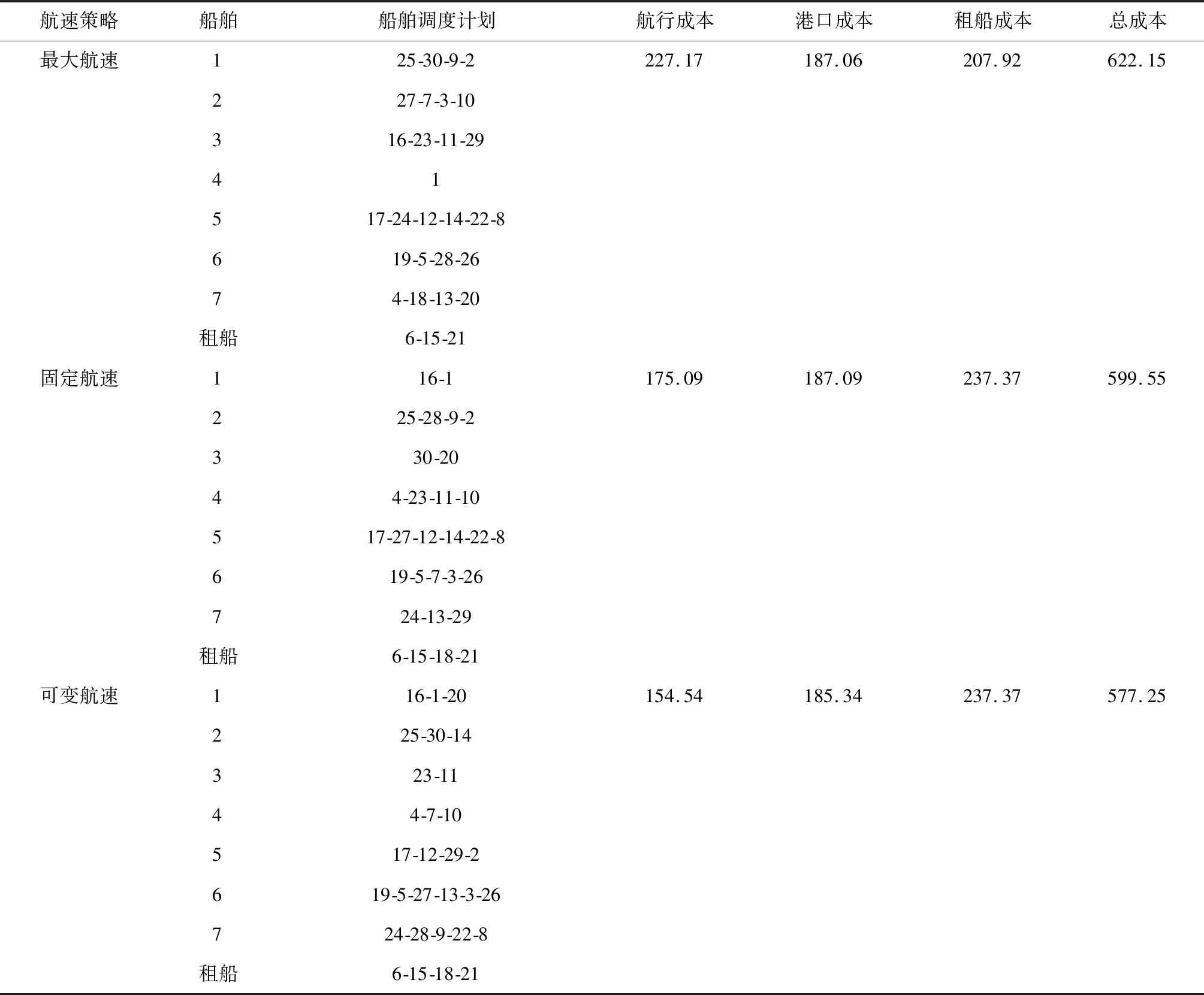
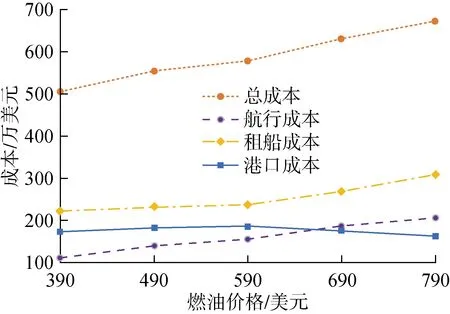
3.4 敏感性分析
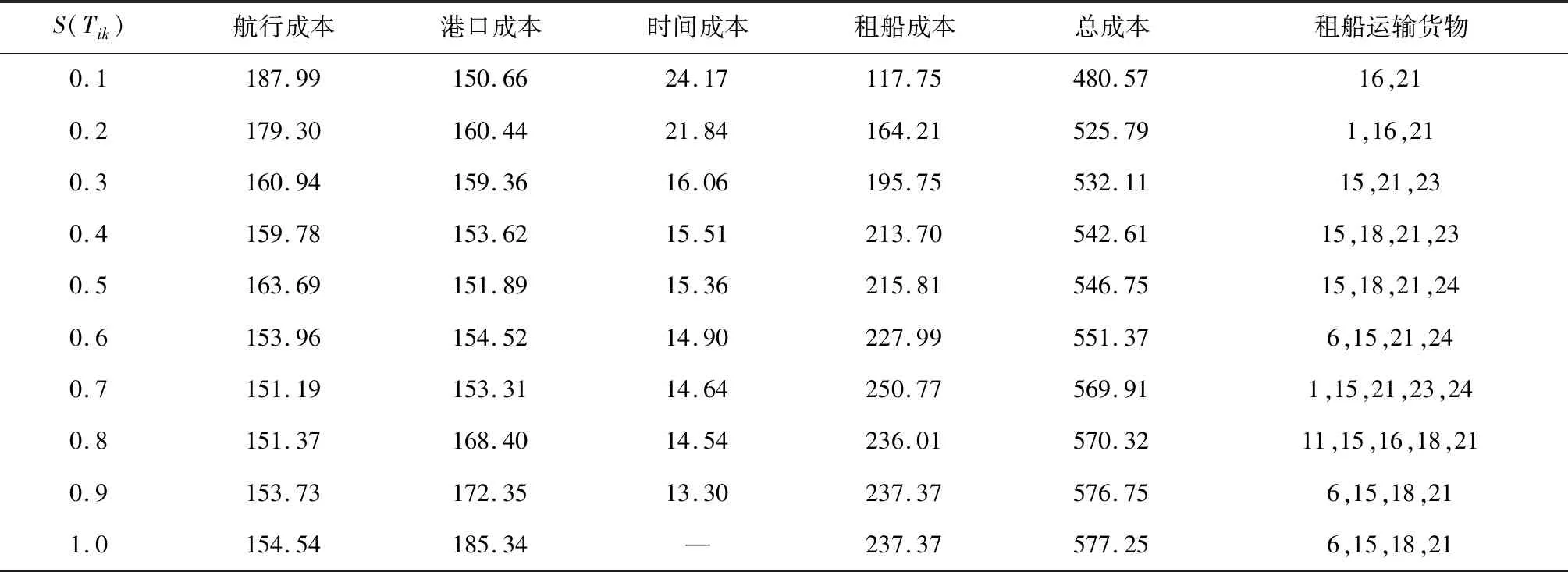
4 結論

