考慮鄰板高程差的裝配式水泥路面行駛舒適性研究

趙蘭若，趙鴻鐸，蔡爵威，吳世濤

(1. 同濟大學 道路與交通工程教育部重點實驗室，上海 201804；2. 中國民航機場建設集團公司西南分公司，四川 成都 610202)

0 引言

裝配式水泥路面是一種面向大面積新建、擴建、加鋪、修復的鋪裝形式，也是實現路面智能化、功能化的平臺[1]。與普通現澆水泥路面不同，裝配式水泥路面采用工廠預制、現場安裝的方式進行鋪筑。由于板塊安裝相互獨立，受多種施工因素影響，相鄰板塊間會不可避免地存在高程差，從而造成路面在板塊接縫處存在間斷式突變，使路面出現不平整。裝配式水泥路面鄰板高程差引起的路面不平整是以板長為波長的路面構造，通常裝配式路面板板長在1～15 m范圍內，按照PIARC對路面構造的分類[2]，此類不平整屬于路面的不平度，會影響行駛的舒適性。

裝配式水泥路面鄰板高程差對車輛產生的不平整激勵與路橋過渡段相類似，因此在研究鄰板高程差對于行駛舒適性的影響時，可以參考在路橋過渡段的相關研究中所采用的分析方法。張洪亮[3]等通過建立車輛模型，考慮車輛上橋和下橋兩個方向以及車路耦合的影響，從振動舒適性的角度提出了不同影響因素下路橋過渡段的容許高程差。與路橋過渡段以及路面隨機振動不同的是，在裝配式水泥路面中，板塊內部相對平整，板塊之間可能存在連續性的高程差，因此會產生連續的階躍瞬變不平整激勵，且隨著板長與車速的不同，相鄰兩個鄰板高程差對于車輛行駛舒適性的影響會存在疊加效應。然而現階段，在裝配式水泥路面的設計和施工中并未考慮鄰板高程差對行駛舒適性的影響。在現有研究中，評價乘客行駛舒適性的方法有很多[4-5]，如乘坐舒適性系數法、吸收功率法、單一不舒適性指數法、汽車振動舒適度法等。在本研究中，參考1997年由國際標準化組織頒布的《機械振動與沖擊——人體承受全身振動的評價》[6]，選取座椅的豎向加權加速度均方根值作為行駛舒適性的評價指標，探究鄰板高程差對于裝配式路面行駛舒適性的影響。

要計算車輛行駛過程中座椅的豎向加權加速度均方根值，關鍵在于獲取車輛在路面不平整激勵下的振動響應，對此，學者們常利用彈簧、質量和阻尼將汽車模型抽象成有限個自由度的力學模型進行理論計算，常用的模型有二自由度1/4車模型、四自由度1/2車模型、七自由度、十一自由度、十七自由度的整車模型[7-13]。其中1/4車模型僅能反映豎向振動，不能反映車輛的轉動和平動；1/2車模型利用車輛左右的對稱性對模型進行簡化，忽略了車輛橫向的傾覆和轉動；整車模型能夠較為真實地模擬車輛實際的振動規律，但自由度數和參數的增多，會使計算變得非常復雜，計算誤差也會相應增大。

在本研究中，主要考慮由鄰板高程差引起的路面縱向不平整，因此假定路面橫向是平整的，選用1/2車模型進行研究。在四自由度1/2車模型的基礎上，增加座椅質心豎向位移作為一個自由度，考慮座椅在行駛過程中的振動。通過計算車輛駛過不同鄰板高程差時振動方程的解，獲取座椅處的加權加速度均方根值，來分析鄰板高程差對裝配式水泥路面行駛舒適性的影響，進而為裝配式路面板的尺寸設計和施工控制提供參考。

1 模型建立

1.1 五自由度1/2車模型

根據鐘陽[14]等的研究結果，輪胎阻尼系數對車輛振動的影響很小，在計算中忽略輪胎的阻尼作用。同時由于波在路面的傳播速度遠大于車輛的行駛速度，并且路面在荷載作用下產生的變形與路面的不平整相比要小得多，因此忽略車輛和路面的耦合作用。由此形成如圖1所示的五自由度1/2理想車模型。

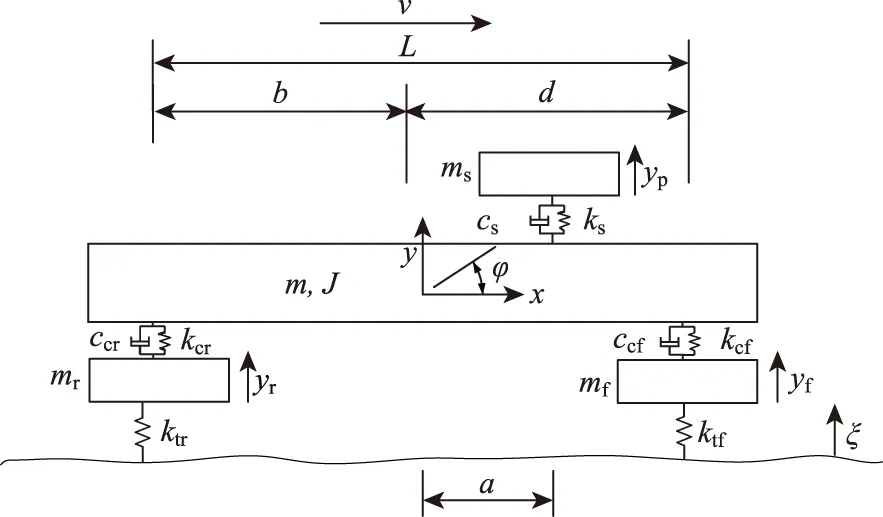
圖1 五自由度1/2車計算模型Fig.1 Five-degree-of-freedom half vehicle model

圖中a，d，b分別為座椅中心、前輪中心、后輪中心到車輛質心的距離；L為前輪中心到后輪中心的距離。

5個自由度分別是：座椅質心處垂直位移ys、前輪胎中心處垂直位移yf、后輪胎中心處垂直位移yr、車架質心處垂直位移y、車架繞質心轉角φ。

ms，mf，mr，m，J分別為座椅和人的質量、前輪非簧載質量、后輪非簧載質量、車架質量、車架繞質心的轉動慣量。cs，ccf，ccr分別為座椅阻尼系數、前懸架系統阻尼系數、后懸架系統阻尼系數。ks，kcf，kcr，ktf，ktr分別為座椅剛度系數、前懸架系統剛度系數、后懸架系統剛度系數、前輪剛度系數、后輪剛度系數。

ζ為路面位移；ζ1，ζ2分別為前輪和后輪的路面位移；v為車速。

依據文獻[15]中采用的模型，在求解過程中選擇典型的小車福特福克斯CAF7810M作為典型的小車車型，具體車輛模型參數見表1。

表1 五自由度1/2車模型參數Tab.1 Parameters of 5-DOF half vehicle model

1.2 汽車振動方程

令u=[ys,yr,yf,y,φ]′，根據達朗貝爾原理，該理想汽車車模型的振動方程如下：

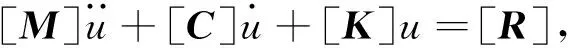
(1)

式中，M為質量矩陣;C為阻尼矩陣;K為剛度矩陣;R為激勵向量。參數含義如下所示。

(2)

(3)

(4)

(5)

要對方程(1)進行求解，需要給定車輪與路面接觸點的位移或荷載，其數值與車輛所受到的不平整激勵有關。因此，需要對車輪經過鄰板高程差時的運動軌跡進行計算和分析。

1.3 不平整激勵

對于裝配式水泥路面，單塊裝配式路面板的表面可看作是完全平整的，即板塊內部的不平整激勵不予考慮。因此裝配式混凝土路面的不平整激勵表現為由鄰板高程差引起的單個或多個等間距出現的間斷性高差。基于此，可通過計算車輛經過接縫時的車輪軌跡，從而獲得車輛在行駛過程中受到的不平整激勵。

將車輪假設為圓盤模型，描述其運動過程。圓盤模型中不考慮車輪與路面的接觸長度，對于普通問題的分析具有一定可行性，但在鄰板高程差分析中，行駛軌跡與輪胎的狀況密切相關，忽略輪胎和路面的接觸長度會引起顯著的差異。本研究參考丁勇[16]等人提出的計算方法，對車輪經過鄰板高程差時的運動軌跡進行計算。計算中假設輪胎與地面接觸為一定接觸長度的圓盤。輪胎向上與向下駛過接縫過程如圖2所示。

圖2 輪胎駛過接縫時軌跡示意圖Fig.2 Schematic diagram of track of tire passing through joint

駛過接縫時輪胎未與路面接觸部分保持圓形、半徑不變，接觸部分為直線，設接觸部分長度為Lt。上接縫過程從輪胎接觸板邊開始，直至輪胎運動到完全在上板位置。設軌跡線AA′為圓弧，在A′處軌跡線與水平相切。輪胎中心軌跡線為O1O2，同樣為圓弧，設O1O2的半徑為R′。通過幾何關系可以推導得到式(6)。

(6)

式中，R′為輪胎中心上接縫行駛軌跡半徑；R為輪胎半徑；Rc為輪胎接地半徑；Δh1為上接縫時的鄰板高程差。

由此可知輪胎接地中心點A的高程函數h(x1)的表達式如下:

(7)

式中，x1為軌跡點到A點的水平距離，其他參數同上。

類似的，下接縫輪底軌跡線為DD′，輪心軌跡線為O3O4。下接縫從輪胎離開上板開始，至完全運動到下板為止。由幾何關系推導輪胎中心軌跡半徑的方法同向上接縫，得到下接縫時輪心軌跡半徑如式(8)：

(8)

式中，Δh2為下鄰板高程差。由此即可得到下接縫中輪胎接地中心D點的高程函數h(x2)。

(9)

式中，x2為軌跡點到D點的水平距離，其他參數同上。

根據式(7)和式(9)即可得到輪胎的運動軌跡，從而獲取路面對車輛的不平整激勵。

2 模型計算與求解

式(1)～(5)描述了五自由度1/2小車模型在不平整激勵下的動力學響應，本研究采用Newmark-β法[17]求解振動微分方程(1)。Newmark-β是一種逐步積分法，求解振動方程較為簡便，并且對非線性問題也具有較好的適應性。

2.1 Newmark-β法求解方法

Newmark-β法的基本思想是對時間步長內加速度變化的分布做出適當的假定，然后通過積分獲得速度變化和位移變化的表達式，進而求得步距末點的值[18]。

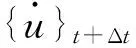
(10)

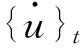
(11)

由此可得t+Δt時刻的振動微分方程如式(12)所示：

(12)

將式(11)代入式(12)，得到關于ut+Δtt的方程如式(13)所示:

(13)

(14)

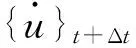
2.2 模型初始條件取值

因采用逐步積分法求解，初始條件對前期求解結果有較大的影響，但是隨著時間的增加，求解結果會逐漸穩定下來。為使求解結果可靠，初始條件應與求解初始狀態相對應。以車輛勻速沿直線行駛為起始狀況，不考慮輪胎和車身懸架在自重下的變形，以此狀態為各自由度豎向位移的起始點。前輪、后輪的初始值為初始條件下的豎向位移值。通過幾何關系來確定車身質心和座椅的初始位移，按下式計算：

(15)

(16)

2.3 加權加速度均方根值及行駛舒適性評價

根據求解得到的車輛節點位移、速度和加速度等指標，可按照式(17)計算座椅加權加速度均方根值。

(17)

式中，aw(t)為瞬時頻率加權加速度值；T為分析的時間長度；t為時間。

加權加速度指對人體最敏感頻率范圍以外的其他頻段的振動加速度進行頻率加權，等效折算為最敏感頻率范圍的振動加速度[6]，用awi表示，與原豎向加速度afi的關系是：

awi=wfiafi，

(18)

式中，wfi為頻率加權函數，可按式(19)進行計算[19]：

(19)

采用加權加速度均方根值對車輛的行駛舒適性進行評價，加權加速度均方根值與行駛舒適性的關系見表2[6]。

表2 加權加速度均方根值與行車舒適性的關系Tab.2 Relationship between WRMSA and driving comfort

3 結果與分析

3.1 單個接縫的影響

為探究單個接縫下，鄰板高程差對于行駛舒適性的影響，計算了不同車速下座椅處豎向加速度隨行駛距離的變化情況，部分計算結果如圖3所示，計算中鄰板高程差高度為5 mm。

從圖中可以看出，在車輛的行進過程中，車輛的前后輪會先后通過接縫，從而產生兩次振動響應，前輪通過接縫時產生的座椅處豎向加速度要明顯高于后輪。車輛在上接縫和下接縫時座椅處豎向加速度的大小相近，方向相反。當車速較低(如10 km/h)時，前輪產生的振動在后輪通過接縫時已經基本消散，兩次振動響應幾乎互不影響；而當車速較高時(如80,160 km/h)，前后輪產生的振動響應會相互疊加，從而產生振動響應的增強或減弱。

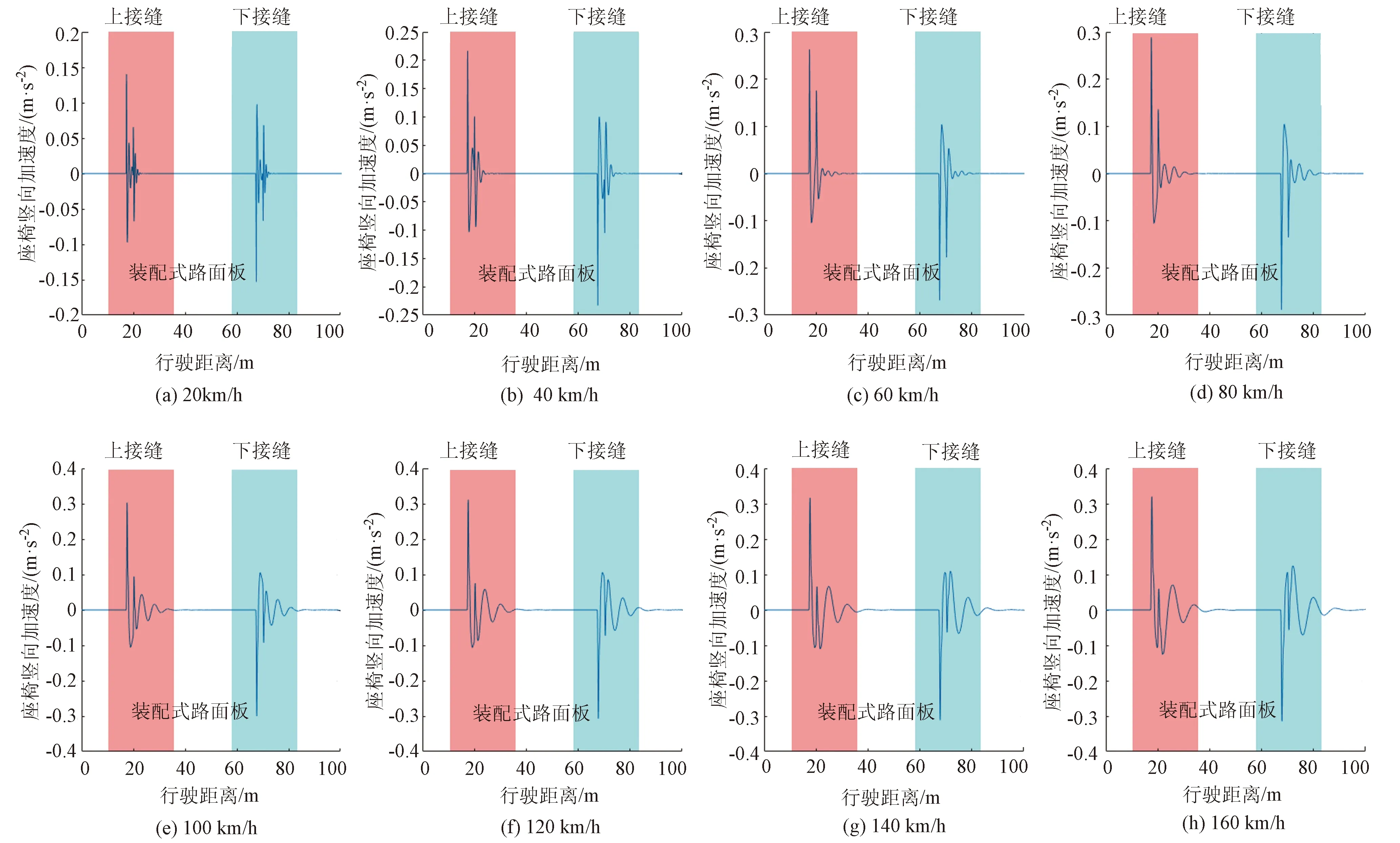
圖3 座椅豎向加速度隨行駛距離的變化情況Fig.3 Vertical acceleration of seat varying with driving distance

3.1.1車速和鄰板高程差的影響

計算不同車速和不同鄰板高程差下座椅豎向加速度的最大值，如圖4所示。結合圖3的結果可知，車速的增大會增加車輛的振動，座椅豎向加速度最大值會隨著車速的增加逐漸增加，但其增長速度會逐漸趨于平緩。座椅豎向加速度最大值與鄰板高程差接近線性關系，鄰板高程差的增大會使座椅豎向的振動更加劇烈，且這種促進作用在車速較高時更加明顯。在上接縫時座椅豎向加速度最大值略高于下接縫，但二者相差不大，最大的相對差值僅為7.4%。

圖4 不同鄰板高程差下座椅豎向加速度最大值Fig.4 Maximum vertical acceleration of seat with different joint faultings

3.1.2接縫影響距離

將從豎向加速度出現第一個峰值到波動峰值衰減到最大值的10%以下時，車輛駛過的距離定義為接縫影響距離，可以計算得到不同鄰板高程差和不同車速下接縫影響距離的大小。計算結果表明，高程差大小及其方向對接縫影響距離影響很小(小于0.01 m)，因此僅給出接縫影響距離隨車速的變化情況，如圖5所示。可以看出，隨著車速的增加，車輛的振動更加劇烈，從而使得接縫影響距離整體呈現上升的趨勢。但是當車速在70～100 km/h之間時，接縫影響距離穩定在2.64 m左右，與前后輪距相等。這是由于前后輪僅在車輪恰好經過接縫時產生較大的座椅豎向加速度，而在車輪通過之后其產生的振動相互抵消，從而導致后續產生的豎向加速度被大大減弱(如圖3(b)、(e)所示)，從而使得接縫影響距離被縮短，其值與前后輪距相等。當車速大于130 km/h后，接縫影響距離則大大增加，這是由于一方面較高的車速下產生的車輛振動響應會更加劇烈，另一方面由于車速較快，前后輪近乎同時通過接縫，后續產生的振動響應相互疊加(如圖3(c)、(f)所示)，從而使得接縫影響距離大幅增大。因此在板長的設計過程中，可根據設計車型和車速計算接縫影響距離，盡可能使板長大于接縫影響距離，避免連續接縫對于座椅豎向加速度產生疊加效應，從而增加行駛舒適性。

圖5 不同車速下的接縫影響距離Fig.5 Joint influence distances at different drying velocities

3.2 多個接縫的影響

3.2.1多個接縫鄰板高程差的模擬

在裝配式水泥路面設計中，設計鄰板高程差為0，但裝配式路面板預制以及現場施工中存在的誤差會導致鄰板間高程差的出現，受多種因素的影響，鄰板高程差通常具有一定的隨機性。

為對多個接縫鄰板高程差進行模擬，假定鄰板高程差呈均值為0的正態分布。在本研究中，實測了某裝配式修復工程中的22塊裝配式路面輪跡帶上鄰板高程差，將行駛方向前板高記為正值、前板低記為負值，得到78個鄰板高程差數據。統計鄰板高程差的分布，計算頻率和頻數，并計算該均值和方差下的正態分布函數值，制成頻數分布直方圖如下。

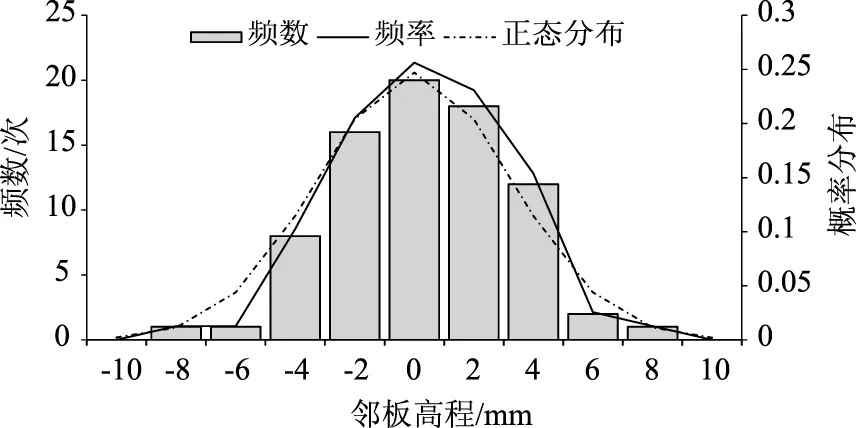
圖6 鄰板高程差分布統計值Fig.6 Statistics of distribution of joint faultings

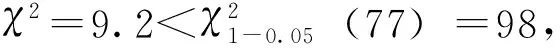
Δh～N[0,σ2]。

(12)

在以下的分析計算中，計算長度取3 000 m，相鄰兩采樣點的水平距離取0.25 m[20]。假定每個接縫處鄰板高程差服從相同的分布，并且相互獨立，按照式(12)給出的分布函數隨機生成路面工況100個，并統計95%分位的座椅豎向加權加速度均方根值作為行駛舒適性的評價指標。得到某一工況下的路面縱斷面形式如圖7所示。

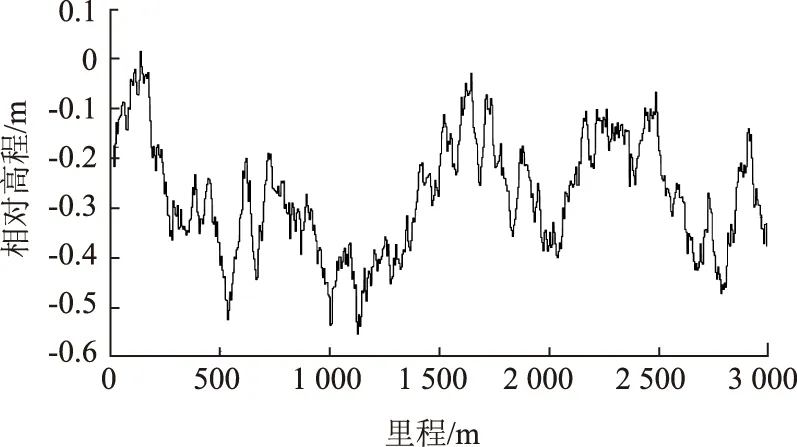
圖7 某一工況下的路面縱斷面Fig.7 Pavement profile in a certain case

3.2.2施工質量的的影響

為探究施工質量對行駛舒適性的影響，計算不同鄰板高程差控制值2σ下座椅豎向加權加速度均方根值，計算中取板長為5 m，計算結果如圖8所示。從中可以看出，加權加速度均方根值與高程差控制值之間表現出明顯的線性正相關性，且車速越大時，高程差控制值對加權加速度均方根值的影響越強。根據表2中加權加速度均方根值與行車舒適性的關系，當加權加速度均方根值小于0.315時，人體會保持舒適，處于0.315～0.63之間時，人體會感到稍不舒適。本研究取0.315 m/s2作為加權加速度均方根值的控制值，由此可以得到設計車速分別為60,80,100,120 km/h下鄰板高程差控制值的最大值，如表3所示。在裝配式路面的施工中可通過提高板塊的預制精度、控制基層整平效果、調節調平螺桿高度等方法，保證鄰板高程差小于表3中的給出的最大值，從而保障車輛行駛過程中具有足夠的舒適性。

圖8 不同鄰板高程差控制值下加權加速度均方根值Fig.8 WRMSAs controlled by of different joint faultings

3.2.3板長的影響

根據3.1.2的分析可知，車輛在裝配式路面板間的行駛舒適性還與板長有關，過短的板長會使車輛通過多塊裝配式路面板時產生更加劇烈的振動，從而使行駛舒適性降低，圖9為不同板長下加權加速度均方根值的變化情況，計算中取鄰板高程差控制值為5 mm。計算結果表明，板長的增加會降低加權加速度均方根值，但這種降低作用會隨著板長的增加而削弱。與之前的分析類似，取0.315 m/s2作為加權加速度均方根值的控制值，由此得到表4所示的不同設計車速下的最小板長，在裝配式水泥路面設計中，在滿足結構受力、板塊運輸、吊裝安全等要求的前提下，可參考表4進行裝配式路面板的平面尺寸設計，當施工質量較高時(鄰板高程差控制值小于5 mm時)，該最小板長可將根據實際設計需求適當放低。

表3 不同設計速度下鄰板高程差的控制值Tab.3 Control values of joint faulting at different design velocities

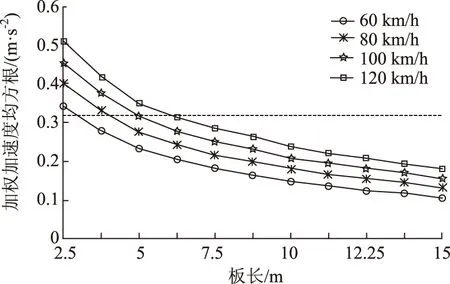
圖9 不同板長下加權加速度均方根值Fig.9 WRMSAs with different panel lengths

表4 不同設計速度下最小板長Tab.4 Minimum panel length at different design velocities

4 結論

本研究通過建立五自由度1/2車模型，對小客車駛過裝配式水泥路面的振動響應進行分析求解，分析了鄰板高程差對行駛舒適性的影響，并得到以下結論：

(1)鄰板高程差引起的裝配式水泥路面不平整對行駛舒適性影響顯著，且受車型、行駛速度、鄰板高程差大小、板長等因素的影響。

(2)在駛過單個接縫時，座椅豎向加速度最大值會隨著車速和鄰板高程差的增加而增加，且它與鄰板高程差呈近線性關系，而車速對它的影響會隨車速的增加而逐漸減弱。

(3)接縫影響距離隨車速呈現整體上升趨勢，對于計算中所用的小客車而言，但當車速在70～100 km/h 之間時，會由于前后輪產生振動的相互抵消使接縫的影響距離減小至與前后輪距相等；而當車速大于130 km/h時，會由于前后輪產生振動的相互疊加使接縫影響距離大幅增加。

(4)在駛過多個接縫時，加權加速度均方根值會隨鄰板高程差的增加而增加，隨板長的增加而減少。在板塊設計和施工中，可以通過控制最小板長、提高施工水平、降低鄰板高程差，來保證路面的行駛舒適性滿足設計的要求。

(5)下一步工作將采用加速度傳感器，通過現場測試對提出的評價方法進行驗證，并探究其他因素如車型、板塊數量等對行駛舒適性的影響。