基于混合改進鳥群算法的貝葉斯網絡結構學習

陳海洋，張 娜

(西安工程大學電子信息學院，西安，710048)

貝葉斯網絡(Bayesian networks,BN)通過概率統計將具體問題進行數據學習后再進行不確定性推理，近年來被廣泛應用于故障分析、數據分析決策、目標識別、態勢評估等[1-3]領域。BN結構學習是BN學習中極其重要的一部分，是通過已知的數據來確定一個最符合數據變量之間連接關系的有向無環圖。BN結構學習方法主要分為3種：①基于約束的結構學習法(constraint-based methods)：該類方法對個體獨立性檢驗的失敗比較敏感，會因某次失敗而導致整個網絡的構建失敗；②基于評分函數的結構學習法(score-search methods)[5-7]：單純通過該方法學習BN結構精確度低、易陷入局部最優，且考慮所有可能的模型耗時長、效率低；③混合法(hybrid methods)[8-10]：常規混合法易陷入局部最優，搜索效率低。這也正是BN結構尋優中最常見缺陷。使用好的仿生智能算法可以很大程度避免陷入局部最優[11-13]。文獻[14]提出生成較優初始種群的方法，并利用改進鯨魚尋優算法進行貝葉斯網絡結構尋優。該方法的尋優效率和準確度都比較好，但復雜度很高。文獻[15]提出用改進后的粒子群算法(particle swarm optimization，PSO)進行BN結構學習，用互信息(mutual information)約束初始網絡后，通過改進的粒子群算法搜索最優貝葉斯網絡，提高了尋優效率，但由于算法不穩定，因此無法保證結構的精確率。

針對上述情況，本文提出將鳥群算法(bird swarm algorithm，BSA)[16-19]應用到BN學習，提出基于混合改進鳥群算法的BN結構學習算法。

1 基于混合改進鳥群算法的貝葉斯結構學習算法

1.1 算法的基本思想

在BN結構學習過程中，可以通過初始數據判斷出節點之間的依賴關系，并用互信息將2個隨機變量之間的依賴度用數值準確地表示出來，如果互信息值越大，兩個變量之間存在連接邊的可能性就越大。因此，輸入一個BN結構的數據，根據各變量之間互信息的值判斷出最優BN結構的候選邊，以此構建初始結構，并生成基于鳥群算法的結構搜索空間。為了提高尋優效率，對鳥群算法做了以下改進：①加入自適應權重，動態調整收斂速度；②改進乞食者和生產者的劃分方式，有利于精準尋優；③根據鳥群的適應度變化差進一步調整自適應權重，減小搜索空間。利用改進的鳥群算法作為搜索策略，并用BIC評分函數對每次更新并處理非法結構[15]后的有向無環圖進行評分，直到迭代次數達到上限，輸出BIC評分最優的結構即為搜索的最優BN結構。

1.2 用互信息構建初始網絡

互信息是度量2個隨機變量之間依賴程度的數學量。依賴程度越強，互信息值就越大。本文算法通過約束初始網絡結構，為改進鳥群算法尋優BN結構提供一個較優的結構空間。

下面給出互信息約束生成的初始網絡偽代碼：

Mutual Information(D,G0,α)

輸入：關于節點X1,X2,…,Xn的數據D，根據數據D隨機生成的初始網絡G0，α為一個常數，maxI(Xi)=0

輸出：互信息約束生成的網絡G1

fori=1,2,…,n

for(除去Xi的節點Xj)

計算節點Xi與節點Xj之間的互信息I(Xi,Xj)

if maxI(Xi)≤I(Xi,Xj)

maxI(Xi)←I(Xi,Xj)

end if

end for

end for

fori=1,2,…,n

for(每個I(Xi,Xj))

ifI(Xi,Xj)≥αmaxI(Xi)

G0中加入Xi與Xj之間的連接邊

end if

end for

end for

G1←G0

returnG1

1.3 改進的鳥群算法作為搜索策略

用互信息約束生成初始網絡之后，本文以改進的鳥群算法作為搜索策略。根據每只鳥在自然界覓食、警戒和遷徙等行為的位置移動更新BN結構。下面給出根據鳥群仿生行為簡化的經典鳥群算法規則：

規則1：每只鳥隨機選擇覓食或保持警覺行為。

規則2：若選擇覓食，每只鳥會記錄并更新其搜索到的最佳覓食位置，并將該最佳位置分享至整個種群。然后，判斷種群最佳覓食位置并記錄下來，根據自身最佳與種群最佳確定下一處覓食。

規則3：若保持警覺，每只鳥為了避免被捕食者追捕，都會試圖飛往種群的中心位置尋求保護，因此就會在種群內部產生競爭，食物儲備多的鳥有更大概率飛往中心。

規則4：鳥群按一定的周期飛往另一區域進行覓食，鳥群中的每只鳥會分享自己覓食信息，食物儲備多的鳥會帶領食物儲備少的鳥去尋找食物。

規則5：將食物儲備最多的鳥稱為生產者，最少的則為乞食者，其他鳥隨機作為二者之一。乞食者會隨機跟隨一位生產者學習覓食方位與位置。

根據規則1～5，將鳥群生物行為分為3種：覓食行為、警戒行為、飛行行為。在此基礎上，對經典鳥群算法進行3部分改進：①在覓食行為中加入自適應權重；②改變經典鳥群算法中乞食者和生產者的劃分方式；③根據鳥群的適應度的變化差調整自適應權重。

1.3.1 覓食行為

根據規則1，鳥群中的每只鳥都會以相同的可能性在(0,1)之間產生一個隨機數，若該數大于常數P時，選擇覓食；若該數小于常數P時，則保持警覺。若選擇覓食，規則2由式(1)表示。在覓食行為中，每只鳥只會依據自己上個時刻的位置經驗去更新位置，這樣會降低整體鳥群搜索空間的自適應性。為此，改進算法通過在每只鳥的位置更新公式前乘以一個自適應慣性權重w(如式(2)所示)來解決這一問題。通過對參數w的調節，控制鳥群的全局搜索能力與局部搜索能力，w較大時，鳥群算法的全局搜索能力強，能夠跳出局部最優，提高算法搜索能力。w較小時，局部尋優能力加強，提高算法的收斂速度。隨著迭代次數增加，w呈線性遞減，鳥群漸漸走向中心位置的最優鳥，見式(1)：

(1)

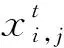
(2)

式中：t是當前迭代次數；tmax代表最大迭代次數；wmax表示初始慣性權重，通常取為0.9；wmin表示鳥群最大迭代次數的慣性權重，通常取0.4。

1.3.2 警戒行為

根據規則3，每只鳥飛往種群的中心位置過程中會與其他競爭者比較食物儲備量，依據比較結果，慢慢飛往種群中心位置，這種行為可由式(3)表示。

(3)

其中

(4)

(5)

meanj為鳥群的平均位置；k是[1,N]之間的隨機整數，且k≠i；N為種群規模；a1,a2是[0,2]之間的常數；pFiti為鳥i的適應度值；ε是計算機中最小的數，用來避免零分割；sumFit為鳥群的適應度之和。

1.3.3 飛行行為

規則4和規則5劃分乞食者與生產者的劃分方式不利于BN結構學習的精準尋優。因此，在算法改進時，改變了劃分方式，即當鳥i的適應度值小于鳥群平均適應度值meanFit時，則稱鳥i為生產者；反之，為乞食者。劃分后，生產者和乞食者的行為分別由式(6)和式(7)描述。

(6)

(7)

式中：rand(0,1)表示產生服從高斯分布的一個隨機數；k∈[1,N]，且k≠i；FL(FL∈[0,1])表示乞食者跟隨生產者尋找食物的概率。

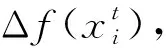
(8)

1.4 用BIC評分函數度量BN結構

本文提出的算法中，鳥群根據適應度值衡量當前網絡結構與初始數據的擬合程度，用貝葉斯信息準則(Bayesian information criterion，BIC)作為適應度函數pFit。根據BIC評分結果更新有向無環圖，并判斷出最優BN結構。BIC評分函數可以度量結構G相對于數據D的優劣：

(9)

式中：隨機變量Xi共有ri個取值1,2,…,ri，其對應的父節點π(Xi)的取值共有qi個，即1,2,…,qi。

1.5 基于混合改進鳥群算法的BN結構學習步驟

本算法步驟流程見圖1。

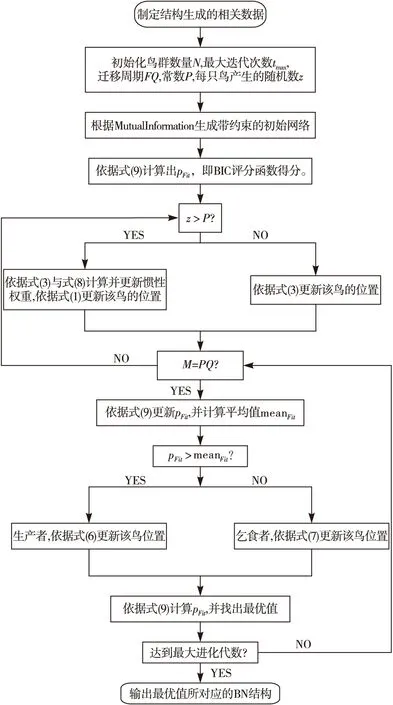
圖1 基于混合改進鳥群算法的BN結構學習流程

2 仿真結果及分析

2.1 測試函數仿真驗證

為了驗證改進算法的有效性，用測試函數將該算法分別與經典鳥群算法、粒子群算法進行比較，見表1。在本次實驗中，群體規模均為20，維度大小為20，最大迭代次數為1 000。通過比較取得最好值和最差值、均值、標準差來證明算法的有效性，3個算法的相關參數設置見表2，實驗結果見表3。

表1 測試函數表

表2 3個算法的相關參數設置表

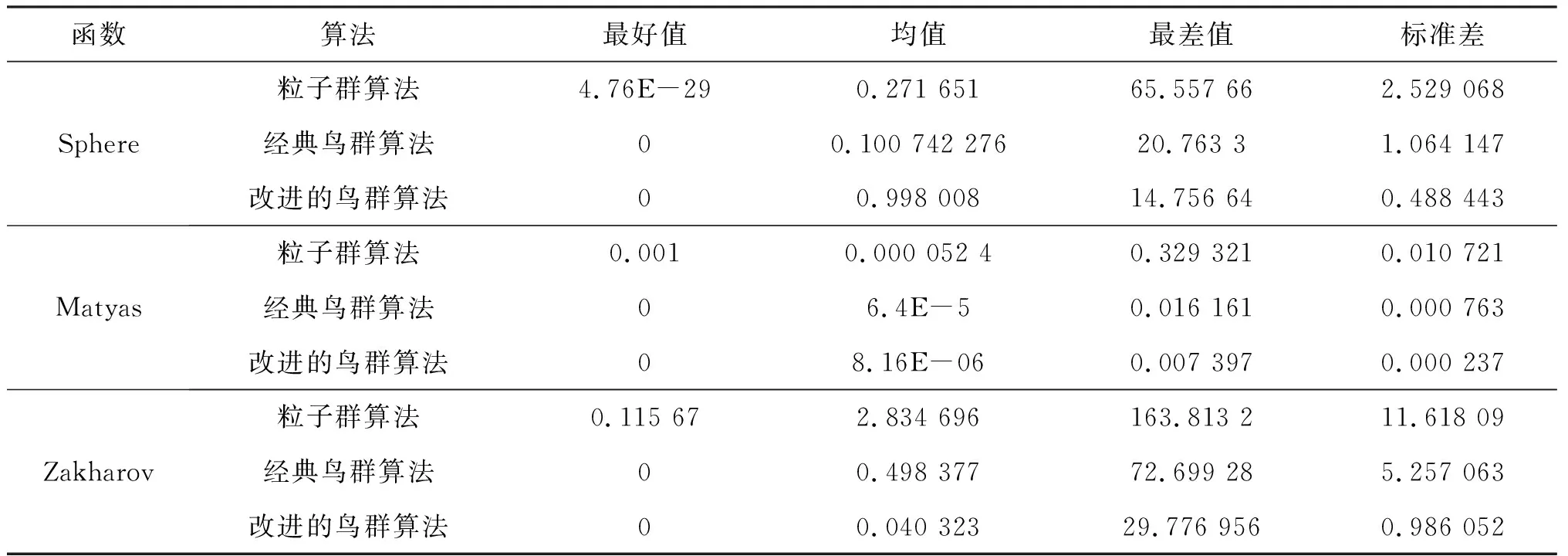
表3 測試函數檢測結果表

從表3中得出，本文算法和經典鳥群算法經過迭代后，都找到了最優值0，而粒子群算法沒有，所以本文算法與經典鳥群算法在尋優能力上都優于粒子群算法，并且本文算法在最差值、均值、標準差方面都相對最低，尋優能力更高。將3個算法在測試函數的尋優過程用圖2～4表示。可以看出，本文算法在3個函數的尋優中都較快找到了最優值0，尋優效率高于其他2種算法。進一步可以說明在迭代過程中動態調整搜索空間后，本文算法的搜索能力更強，且收斂性也進一步提高。

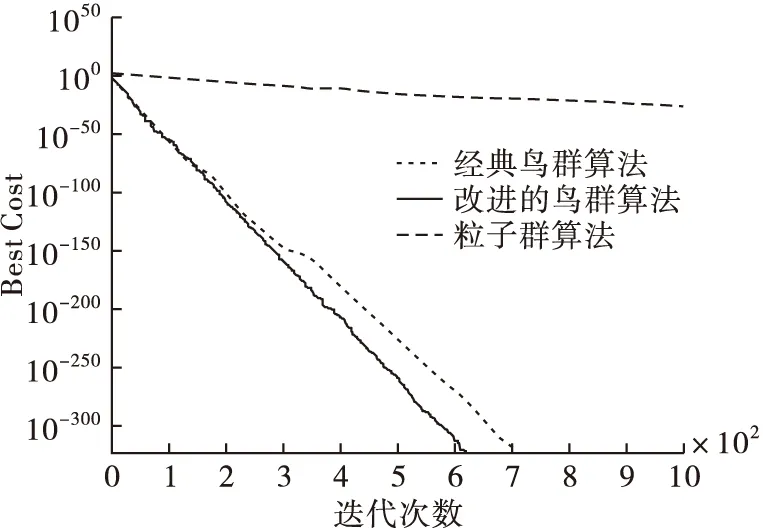
圖2 3個算法在Sphere函數中的尋優過程比較

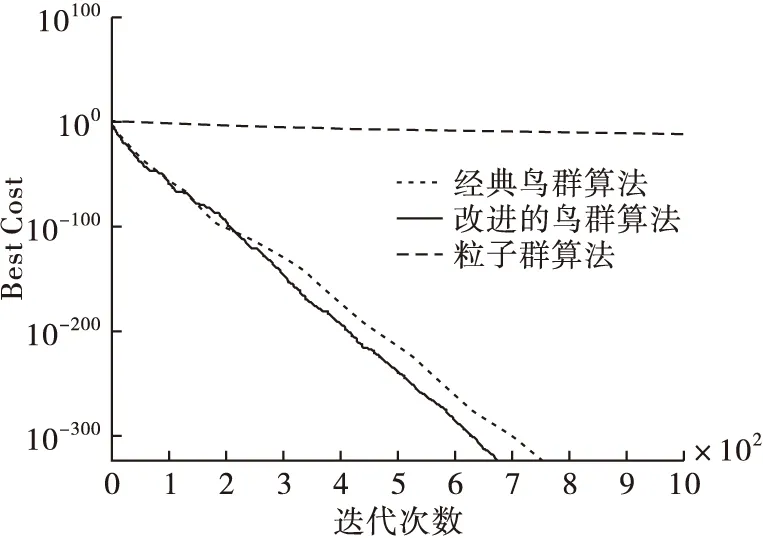
圖3 3個算法在Matyas函數中的尋優過程比較

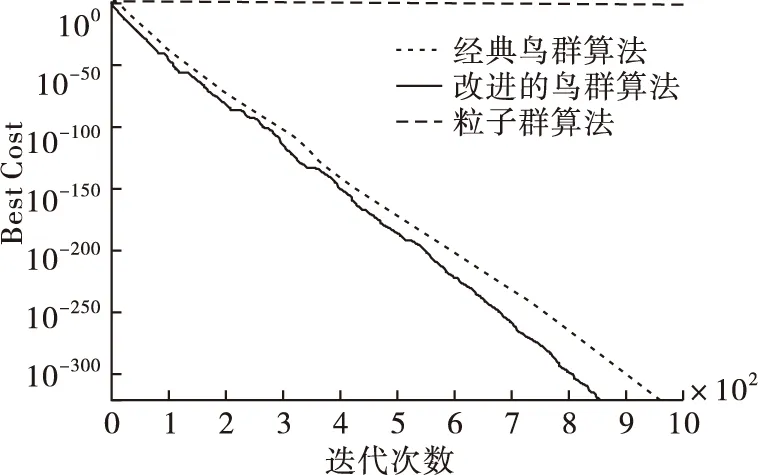
圖4 3個算法在Zakharov函數中的尋優過程比較

2.2 BN結構學習仿真驗證

為了驗證基于混合改進鳥群算法的BN結構學習的尋優準確性、全局收斂性，把它與經典鳥群算法、粒子群算法、K2算法、MCMC算法的BN結構學習進行比較，將這5種算法分別應用于動物特征(AC)網絡(7個節點，6條有向邊)與胸部診斷(ASIA)網絡(8個節點，8條有向邊)。這兩種網絡分別產生數據量為100個、500個、1 000個、3 000個的樣本各10組。將算法在每組數據樣本上獨立運行10次，每次迭代50次，結果取平均值。本文算法參數設置為種群規模=20，α=0.6，FQ=3，a1=a2=1，C=S=1.5，FL∈[0.5,0.9]，P∈[0.8,1]，粒子群算法、經典鳥群算法參數設置見表2。K2算法的節點序為互信息生成的候選邊的隨機節點序，MCMC算法參數為貝葉斯工具箱默認參數。貝葉斯網絡結構學習算法的常用度量指標見文獻[20]。仿真結果如表4和表5所示。

由表可知，本文算法的C值均大于經典鳥群算法、粒子群算法、K2算法、MCMC算法。本文算法的FA、FM、FR、F各值也都小于其他4個算法的值。從C列與F列可以看出，隨著數據量的增大，本文算法的C值逐漸增大，F值逐漸減小，說明得到的BN結構越來越接近標準結構。從兩個網絡的BIC列值可看出，在數據量較小時，本文算法的BIC評分優于經典鳥群算法、粒子群算法、MCMC算法，但稍低于K2算法，這是由于提前給定了K2算法的節點序列，而在實際應用中，很難較準確地給出。但是隨著數據量的增加，本文算法的BIC評分超過了K2算法，為了進行更細致地分析，現將2個網絡中500、1 000、3 000數據量下的BIC評分值進行比較，結果見圖5。

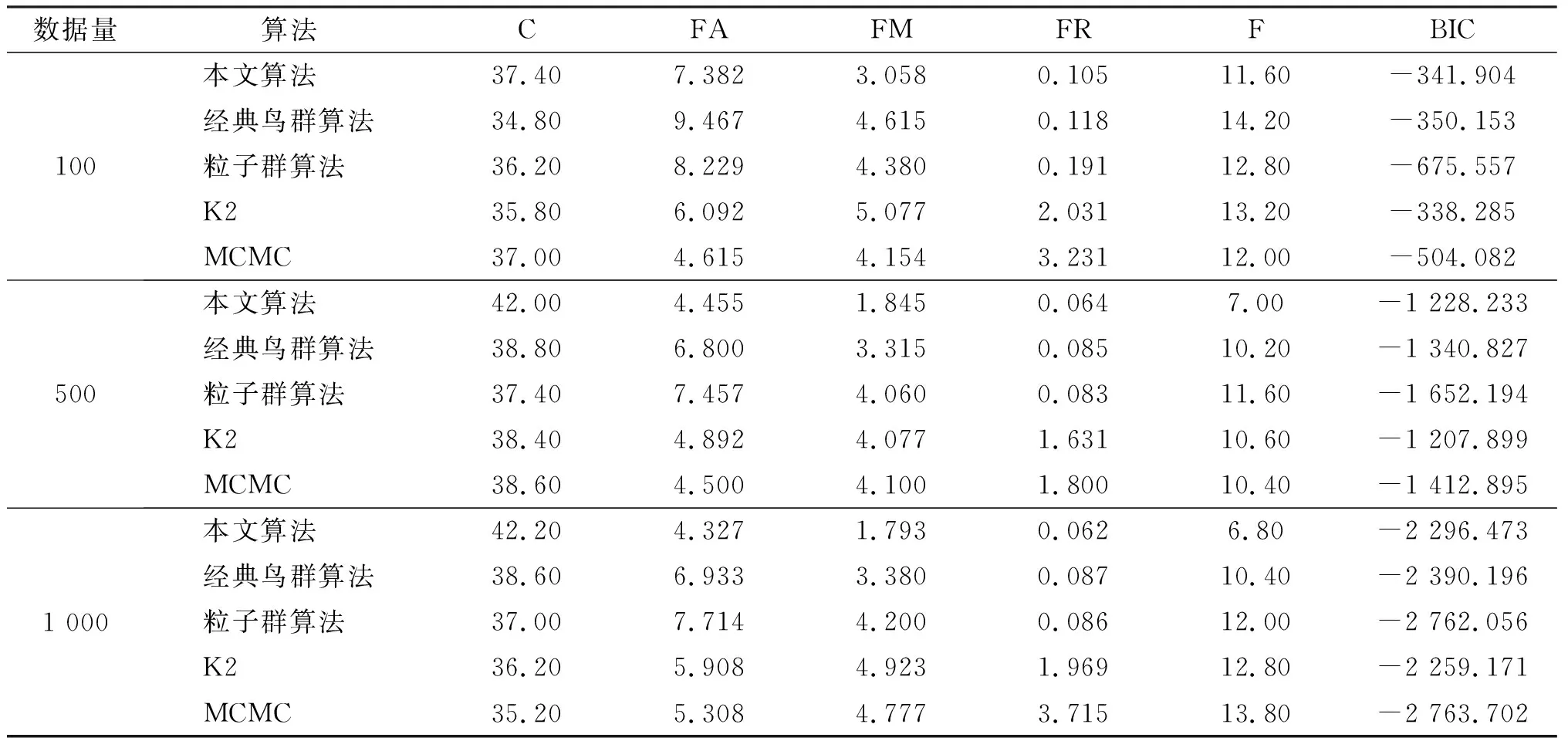
表4 不同算法在動物特征網絡中的對比

續表

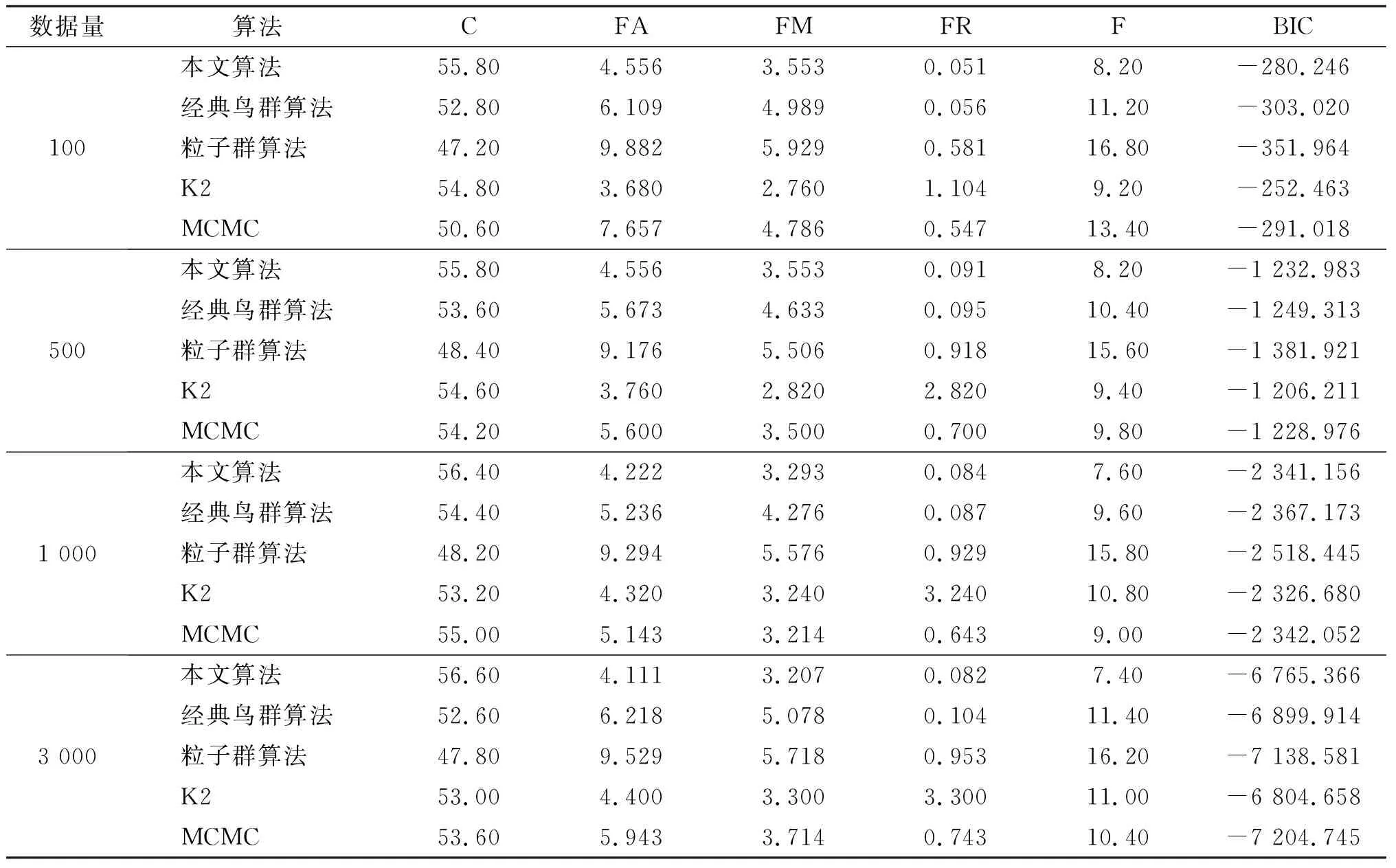
表5 不同算法在胸部診斷網絡中的對比

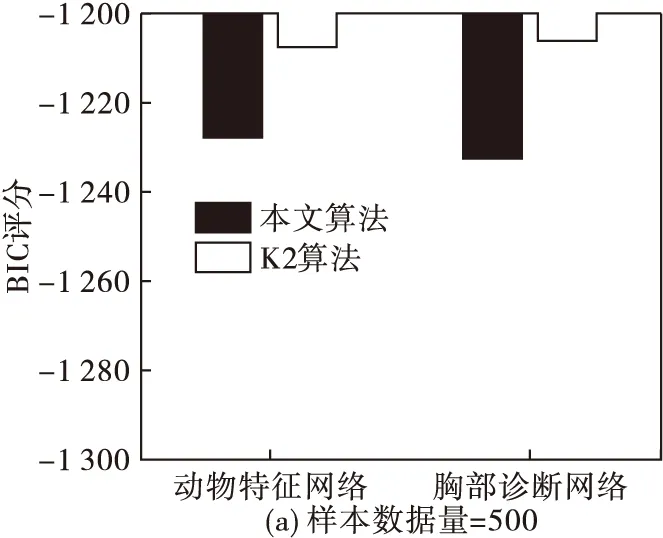
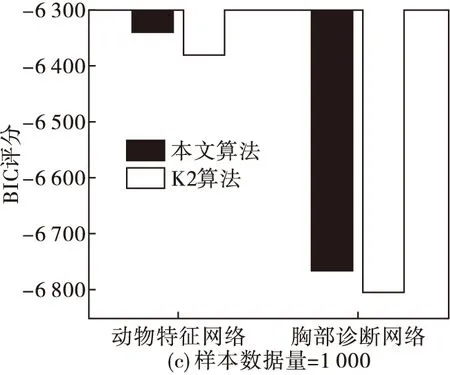
圖5 不同數據量下本文算法與K2算法在動物特征網絡與胸部診斷網絡中的BIC評分比較

從圖5可以看出，當數據量為500、1 000時，K2算法的BIC評分要稍微大于本文算法，但數據量增加為3 000時，本文算法的BIC評分較大。這就說明當數據量較大時，本文算法的結果更擬合初始數據樣本。同時，為了進一步體現本文算法較其他仿生算法的搜索能力及收斂過程，分別在數據量為100、500、1 000、3 000的情況下，將本文算法與經典鳥群算法、粒子群算法在動物特征網絡應用中的BIC評分在迭代過程中的變化進行比較，結果如圖6。可以看出，在相同數據量下，本文算法的在搜索過程中逐步優于其他兩個仿生算法，并且隨數據量的增加，優勢更加明顯，說明本文算法在BN結構的應用中較其他算法尋優能力高，收斂性好。

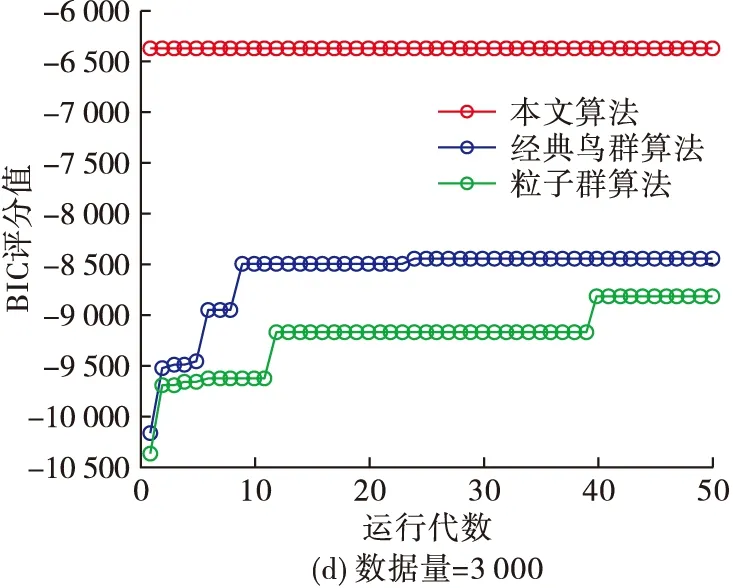
圖6 不同數據量下3個算法的BIC評分比較

綜上所述，本文算法在6個度量BN結構學習的常用指標上都優于經典鳥群算法、粒子群算法、K2算法、MCMC算法。說明本文算法用互信息生成的初始網絡，縮小了搜索空間。同時改進的鳥群算法也在全局性和局部性中保持了良好的平衡，為搜尋最優網絡提供了一定的保障。

3 結語

目前，混合智能仿生算法成為了BN結構學習中的研究熱點，該方法既利用了約束生成的初始網絡，又利用了智能算法不易陷入局部最優的優點，從而有效改善了BN結構學習尋優效率低下、易陷入局部最優的缺陷。本文提出的基于混合鳥群算法的BN結構學習，通過互信息約束初始尋優網絡，為搜尋最優網絡結構提供了較好的搜尋空間。同時引入自適應慣性權重，動態調整鳥群算法的收斂速度，優化了易陷入局部最優問題，提高了尋優效率。實驗結果證明，本文提出的算法準確率高，尋優性能好。