Ni- Re與Co- Re二元體系的熱力學研究及相圖

史中文 夏成輝 劉 微 魯曉剛,

(1.上海大學材料科學與工程學院，上海 200444； 2.上海大學材料基因組工程研究院，上海 200444)

20世紀80年代，鎳基高溫合金成功應用在航空發動機上，這一突破性進展促進了鎳基高溫合金的迅速發展。目前鎳基高溫合金廣泛用于制造航空航天和許多其他行業的發動機和汽輪機的葉片[1]。

研究表明：在高溫合金中添加Re等難熔金屬元素可以有效提高高溫合金的疲勞性能和抗蠕變性能[2- 3]，但同時會造成元素偏析，在高溫服役條件下易析出TCP相，降低合金性能。而Co等元素的添加可以有效地降低難熔元素的偏析，控制TCP相的形成和長大，提高高溫合金的高溫蠕變性能[4]。確定Ni- Re和Co- Re等合金體系的相圖和熱力學性質是提高高溫合金性能的前提。但目前對于Ni- Re和Co- Re體系的研究還不夠充分，導致這兩個體系的相圖和熱力學性質還存在一些問題。雖然近幾年由于高溫合金的發展，越來越多的研究者開始重視并重新評估這些體系，一些試驗數據得到了更新及補全，但仍不夠全面。本文結合現有相圖試驗數據及第一性原理計算結果，重新評估了Ni- Re和Co- Re體系的熱力學數據及相圖。

1 文獻調研

1.1 Ni- Re體系

1985年，Nash等[5]在Savitskii等[6- 7]研究的基礎上，結合相平衡試驗數據、晶體結構數據等，評估了Ni- Re二元系的相圖，但得到的相圖與試驗數據不太吻合。1992年，Okamoto[8]重新研究了Ni- Re體系，并對以前的部分相圖進行了修改，得到了更合理的優化相圖。1999年，Huang和Chang[9]利用與Okamoto不同的純組元熱力學數據重新評估了Ni- Re相圖，得到了與Savitskii等的試驗數據較為吻合的相圖。2012年，Yaqoob和Joubert[10]結合近幾年的研究數據[11- 12]，提出了新的Ni- Re相圖，擴大了hcp相的范圍，并對fcc相范圍進行了調整，得到了更為準確的相圖。

1.2 Co- Re體系

Co- Re體系最早由Koster和Horn[13]研究，Savitskii與Tylkina[14]確定了整個體系的固相線，Elliott[15]則修正了前人研究中的一些問題。1993年，Predel[16]在前人試驗數據的基礎上重新評估了Co- Re二元體系，并給出了二元系的相圖。2005年，Takeuchi和Inoue[17]用Miedema模型計算得到了Co- Re體系4 000 K下的液相混合焓。2014年，Liu等[18]優化了熱力學數據并得到了新的Co- Re相圖。2018年，Guo等[19]為了建立鎳基高溫合金數據庫重新評估了Co- Re體系，同時也改進了該二元相圖。2019年，Fedorayev等[20]在研究Co- Re- Ta體系等溫截面時得到了兩組Co- Re體系的相平衡數據，但與之前的相圖存在差異。

2 第一性原理SQS計算

第一性原理計算(first- principles calculation)方法又稱從頭計算法(ab initio calculation)，只需要輸入元素及結構信息就可以通過薛定諤方程(Schr?dinger equation)合理預測材料的各種物理化學性質和電子狀態[21]。密度泛函理論(density functional theory,DFT)[22]是第一性原理計算的基礎，其主要目標是用電荷密度函數代替復雜的多電子波函數作為基本變量，從而實現電子結構的計算。

本文利用VASP(Vienna ab initio simulation package)軟件包[23]，采用平面波方法和投影綴加波(projected augmented wave,PAW)[24]贗勢法，交互關聯泛函采用GGA- PW91[25]，進行了自旋極化計算，設置了鐵磁性的磁性參數。平面波截斷能取400 eV。使用Monkhorst- Pack包[26]構造布里淵區k點網格，k點的總數乘以單胞的原子數至少為7 200。利用特殊準隨機結構(special quasirandom structures, SQS)[27]方法產生無序結構，構建了16個原子的超胞，包括如下成分結構，即A1B15、A4B12、A8B8、A12B4和A15B1。為了在VASP計算過程中自動產生輸入文件以方便計算，本文使用了ZenGen腳本工具[28]。

3 試驗材料與方法

將純度(質量分數)均為99.99%的Ni、Re和Co 3種純金屬原材料按照合金成分進行稱重配料，制備試樣。采用WK- II型電弧感應熔煉爐熔煉，得到所需成分的合金紐扣錠。隨后將試樣密封在氬氣保護的石英管中，再將石英管置于馬弗爐中加熱至1 473 K保溫72 h后水淬，以消除偏析并提高成分均勻性。將淬火后的試樣線切割加工成4 mm×4 mm×4 mm的正方體和直徑4.9 mm、高度18 mm的圓柱樣，然后清洗除去表面油污，并用金相砂紙打磨拋光，確保后續處理不會有雜質影響。將正方體試樣密封在氬氣保護的石英管中，然后置于管式爐中加熱至一定溫度，保溫一定時間后水淬，具體方案如表1所示。正方體試樣經打磨拋光后采用電子探針(EPMA)測定相成分。最后使用MHTC96高溫量熱儀對圓柱形試樣進行差熱掃描分析(DTA)，測定其相變點。

表1 合金成分及試驗條件Table 1 Compositions of the alloy and experimental conditions

4 熱力學模型

Ni- Re和Co- Re體系中的液相、fcc和hcp相都可以采用置換溶體模型來描述，其摩爾吉布斯自由能函數為：

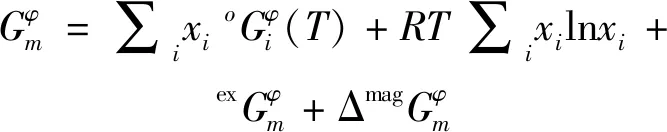
(1)

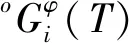
(2)

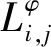
(3)

5 結果與討論

5.1 Ni- Re體系

1999年Huang和Chang[9]重新評估了Ni- Re相圖，得到了與Savitskii等[6- 7]的試驗數據較為吻合的相圖。但是近些年對Ni- Re體系的一系列研究都表明hcp相的實際相區更大，并且在富Ni端的試驗數據也與計算相圖不符，故Yaqoob和Joubert[10]結合近幾年的研究數據[11- 12]，提出了新的Ni- Re相圖，具體數據列于表2。如圖1所示，Yaqoob和Joubert計算得到的相圖中hcp相區較Huang和Chang的明顯擴大，且對fcc相區進行了調整，與近些年的Ni- Re的相平衡數據比較吻合。

本文對Yaqoob和Joubert[10]計算得到的相圖也進行了驗證。將Ni- 30Re合金(1號合金)在1 523 K保溫72 h得到了一組相平衡數據，發現平衡點與Yaqoob和Joubert的結果十分接近。此外，對Ni- 30Re合金進行了DSC測試，測得其包晶溫度為1 832.98 K，比Yaqoob和Joubert的計算結果略高。

表2 Ni- Re相平衡試驗數據Table 2 Experimental data of the Ni- Re phase equilibrium

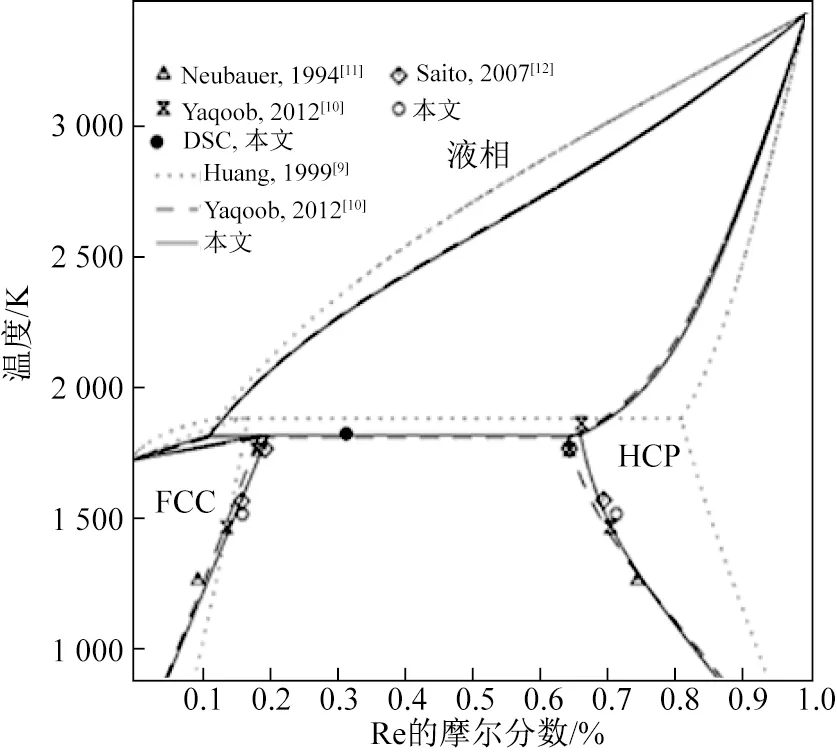
圖1 優化的Ni- Re相圖與試驗數據對比Fig.1 Comparison of the optimized Ni- Re phase diagram with the experimental results

但研究發現，Yaqoob和Joubert[10]在熱力學評估時僅考慮了相平衡點數據，并未考慮其他熱力學性質，在外推到高元體系時容易產生問題，所以本文在相平衡數據的基礎上，同時考慮其他熱力學性質，以得到更為準確的熱力學參數。

Hofmann[29]研究發現，當Re的質量分數達到18%左右時，Ni- Re系合金中fcc相的居里轉變溫度為273 K；當Re的質量分數達到30%左右時，居里溫度接近0 K。Huang和Chang[9]及Yaqoob和Joubert[10]的評估都未涉及此問題。本文對此進行了研究，基本能反映Ni- Re合金的居里溫度隨合金成分變化的規律，對比結果如圖2所示。此外，還對第一性原理SQS計算所得的混合焓及磁矩進行了研究，結果如圖3和圖4所示。

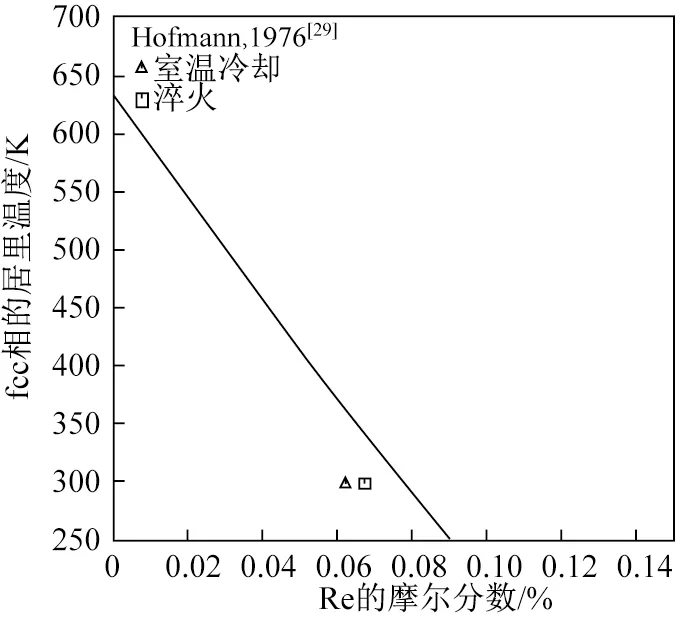
圖2 Ni- Re體系fcc相優化的居里溫度與試驗數據對比Fig.2 Comparison of the optimized Curie temperature of fcc phase in Ni- Re system with the experimental data

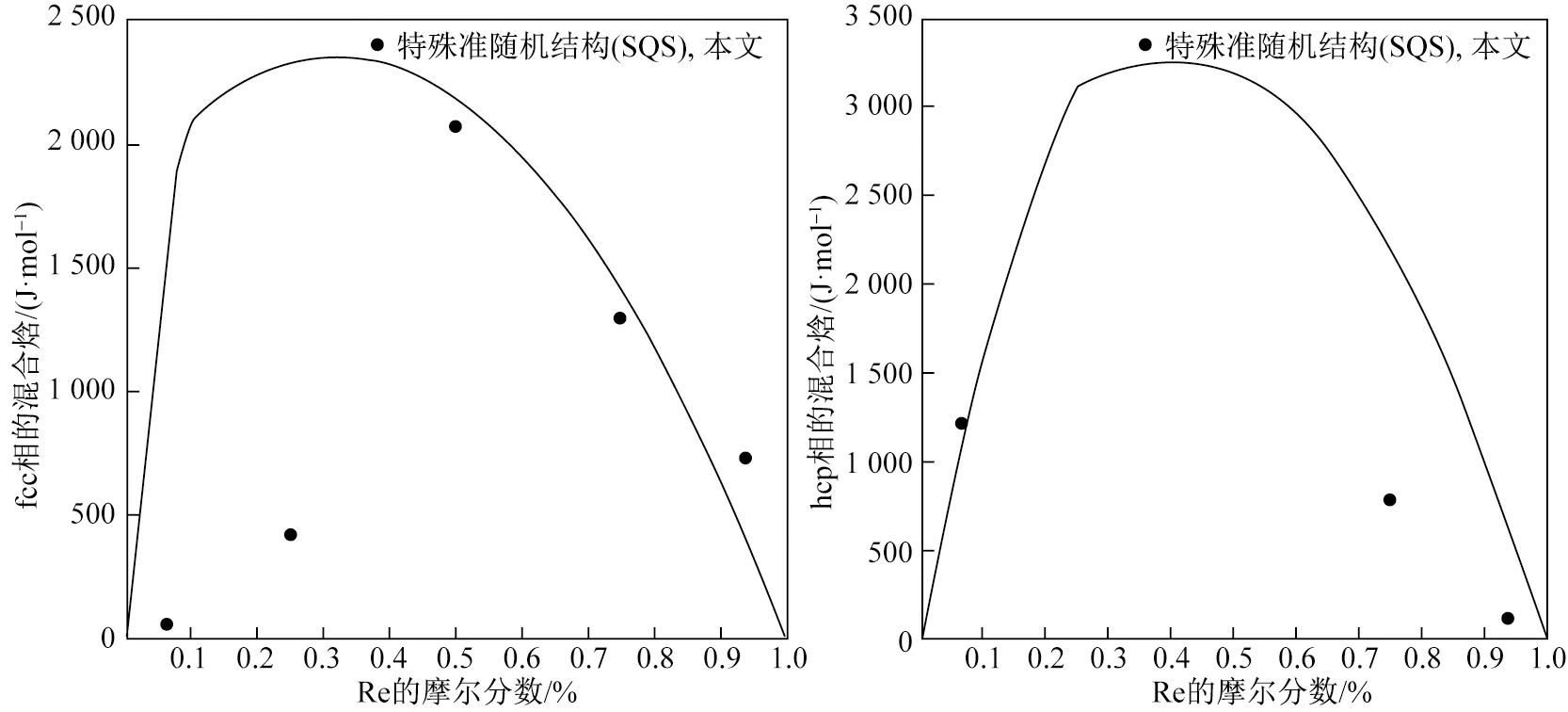
圖3 優化的Ni- Re fcc相和hcp相的混合焓與特殊準隨機結構(SQS)數據的對比Fig.3 Comparison of the optimized mixing enthalpy of fcc and hcp phases in Ni- Re system with the SQS data

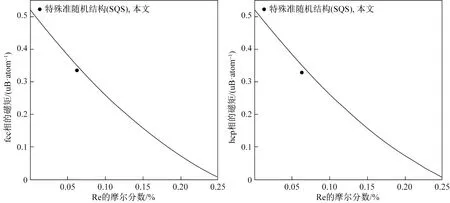
圖4 優化的Ni- Re fcc相和hcp相的磁矩與特殊準隨機結構(SQS)數據的對比Fig.4 Comparison of the optimized magnetic moment of fcc and hcp phases in Ni- Re system with the SQS data

綜合以上研究重新評估得到新的相圖如圖1所示。與Yaqoob和Joubert[10]的相圖相比， 新相圖中的包晶反應溫度提高，該溫度下Ni在Re中的最大溶解度增大，與本文試驗數據更為吻合，同時也與其他數據較為符合。

5.2 Co- Re體系

Liu等[18]在前人研究的基礎上優化了Co- Re相圖。2018年，Guo等[19]為了建立鎳基高溫合金數據庫，重新評估了Co- Re二元系的試驗數據，優化了該體系的相圖。Liu等與Guo等評估的相圖與試驗數據的比較如圖5所示。從圖5可以看出，兩者差別不大，僅在溶解度曲線上略有差異，并且從文獻中可知，二者均未找到原始試驗數據，都是從Predel[16]的試驗相圖上描點來驗證各自計算相圖的。由于缺乏試驗數據，對現有Co- Re體系相圖的準確性還無法有效驗證。

2019年，Fedorayev等[20]在研究Co- Re- Ta體系等溫截面時得到了兩組Co- Re體系的相平衡數據，如表3所示。可見，Fedorayev得到的平衡點與現有相圖差異較大，相對于原來的相界向右偏移，落在了現有相圖的兩相區和hcp相區。為了驗證現有相圖的準確性，本文也進行了試驗研究，結果如圖5所示，發現預計落在兩相區的合金點是單相，表明現有相圖存在問題，需進一步研究。

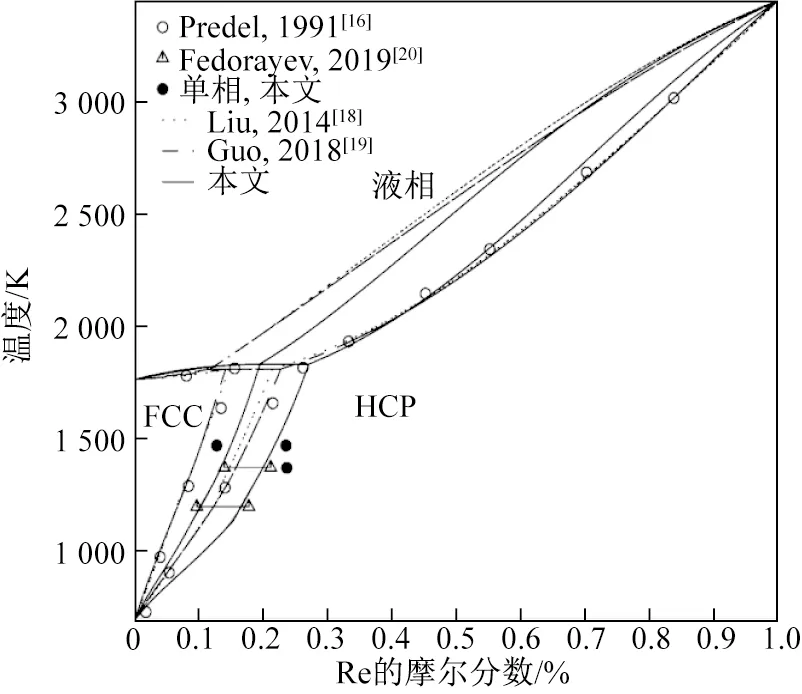
圖5 優化的Co- Re相圖與試驗數據對比Fig.5 Comparison of the optimized Co- Re phase diagram with the experimental data

Guo等[19]在研究Co- Re體系時，引入了一系列熱力學參數，但未與試驗數據進行比較，所以無法判斷這些參數的準確性。本文根據第一性原理SQS計算得到的混合焓及磁矩，對Co- Re體系的熱力學參數進行了重新評估，對比結果如圖6和圖7所示。可見用當前熱力學參數計算的結果與第一性原理計算結果較吻合。此外，Takeuchi和Inoue[17]利用Miedema模型計算得到了Co- Re體系4 000 K下的液相混合焓，與本文試驗數據的對比如圖8所示，兩者吻合較好。

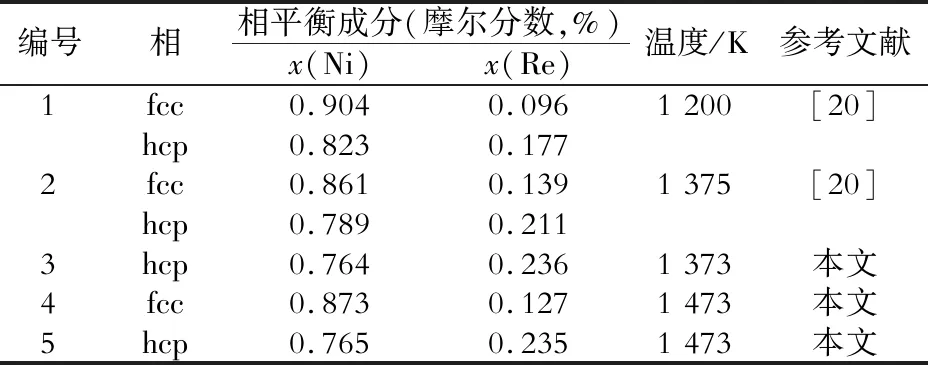
表3 Co- Re相平衡試驗數據Table 3 Experimental data of the Co- Re phase equilibrium

圖6 優化的Co- Re fcc相和hcp相的混合焓與特殊準隨機結構(SQS)數據的對比Fig.6 Comparison of the optimized mixing enthalpy of fcc and hcp phases in Co- Re system with the SQS data

圖7 優化的Co- Re fcc相和hcp相的磁矩與特殊準隨機結構(SQS)數據的對比Fig.7 Comparison of the optimized magnetic moment of fcc and hcp phases in Co- Re system with the SQS data

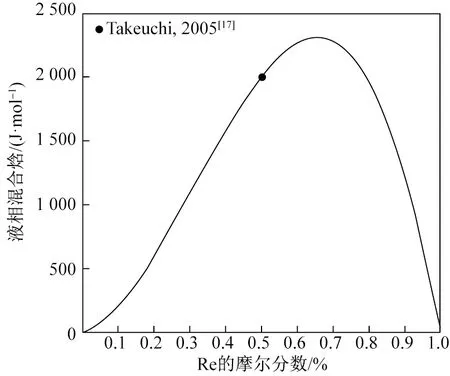
圖8 優化的4 000 K下Co- Re液相的混合焓與試驗數據的對比Fig.8 Comparison of the optimized mixing enthalpy of liquid phase in Co- Re system at 4 000 K with the experimental data

綜合以上結果，重新計算得到的新相圖如圖5所示，與Liu等[18]及Guo等[19]的相圖及試驗數據進行對比，發現新相圖的兩相區右移，與Fedorayev等[20]的試驗數據基本一致，并且單相區范圍與試驗結果一致，表明本文優化的相圖更為合理。

6 結論

運用CALPHAD方法和Thermo- Calc軟件，結合近年文獻及本文測定的試驗數據，加之第一性原理SQS計算結果，重新評估了Ni- Re和Co- Re二元體系，得到了新的二元相圖以及一系列熱力學參數。計算得到的相圖和熱力學性質與試驗數據、第一性原理計算結果自洽良好。新相圖及熱力學數據可以作為外推高元體系的基礎，對鎳基高溫合金的研究具有重要意義。