基于改進的Morlet小波變換在伊犁盆地南緣層序地層劃分中的應用

苗辰若,高曉偉

(核工業二一六大隊，烏魯木齊 830011)

0 引言

層序界面的劃分和地層對比在地層評價工作中占有重要地位，正逐漸由定性走向定量、由宏觀走向微觀，其在砂巖型鈾礦中有著廣闊的應用前景[1-2]。相對于提取地震屬性[3]，無論是縱向分辨率還是連續性，測井資料都是最好的一種地質資料，是對地層某個特定的物理參數隨著深度變化的反映，包含的地質信息豐富，是當前進行地層劃分與對比最成熟的手段。隨著測井技術的進步，測井數據的地質屬性為層序劃分和地層對比方面的研究提供了很好的條件。通過對測井曲線的分析，可以將其包含的地質信息和地質屬性直觀地體現出來。

應用測井曲線進行基準面旋回劃分，結果因人而異，原因在于測井曲線所反映的沉積序列，本質上是各個地質周期沉積響應的疊加，人為判斷并劃分地質周期會存在主觀隨意性。小波變換[4]可以從復雜多變的原始測井信號中識別提取出信號的時頻特征，以多種尺度、多種分辨率對測井信號中的周期成分進行探測[5]。傳統的Morlet小波在地球物理數據處理、地質屬性提取等方面較其他小波分析方法有優勢，但其不滿足小波的容許條件，無法對處理信號進行逆變換，所表達的地質、地球物理信息仍然較為模糊。通過對傳統Morlet小波進行改進，并利用改進后的Morlet小波，將一維測井信號轉換為二維深度-尺度信息，通過振幅譜和相位譜信息有效地識別旋回類型、層序地層界面，取得了較好的效果。

1 小波變換

1.1 原理

小波是一個衰減的波形，它在有限的區域里存在(不為“0”)，并且其均值為“0”。

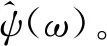
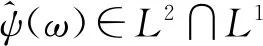
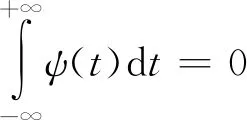
(1)

(2)

式中：ω為角頻率；ψ(t)為一個基本小波(小波基)或母小波(Mother Wavelet)，式(1)被稱為容許條件，也被稱為容許小波。

Cf(a,b)=〈f,ψa,b〉=

(3)

式(3)被稱為f以ψ為基的小波變換。

對小波基進行伸縮平移變換，得到一個小波函數簇，如式(4)所示。

a,b∈R,a≠0

(4)

式中：a為尺度參數;b為時間平移參數；ψa,b(t)為小波基函數。當a、b時連續變量時，稱之為連續小波變換(CWT)。

小波變換的示意見圖1。由圖1看出，小波變換可給出各個時刻由不同尺度和不同位置的小波構成的信號。

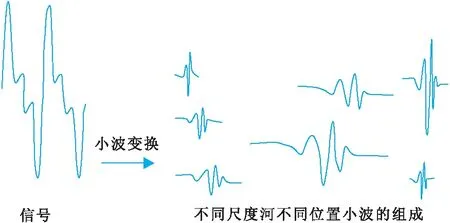
圖1 信號小波變換示意圖Fig.1 Schematic diagram of signal wavelet transform

從本質上看，小波變換本質上是一種積分變換，包含兩個參數(尺度參數、時間平移參數)，經過小波變換后，時間函數被投影到二維的時間-尺度平面上，可用來更好地分析周期特征。

圖2為某鉆孔測井信號經Morlet小波變換后的尺度參數圖。同一個沉積周期的測井曲線經小波變換后的小波系數具有了相同的振蕩幅度，不同尺度的小波變換實現由粗到細分級別的層序劃分奠定了基礎。尺度參數與地層沉積周期和頻率對應，①大尺度對應低頻、長周期的地層，可用于劃分大的層序地層；②用中等尺度代表中等周期的地層層序；③小尺度對應高頻、短周期的沉積地層，由于層序級別越小，內部的自旋回沉積現象越多，對層序旋回的干擾也就越大，對于這種級別的層序，不能用高頻部分確定。

1.2 最優小波的選取

運用較多的小波有Daubechies(Db)小波、Morlet小波、Meyer小波等幾種，每種小波的函數和形態有所不同，所有滿足小波條件的函數都可以作為小波函數。

實際應用中選擇小波類型的原則主要有3種[7]：

1)自相似性原則。若選擇的小波對信號有一定相似性，則變換后的能量比較集中，可以有效減少計算量。

2)判斷函數。針對特定的問題找到關鍵性的技術指標和參數，得到的函數即判斷函數，然后再將各種小波函數代入，得到最優函數。

3)支集長度。大部分應用選擇支集長度為5 m～9 m的小波，避免支集太長產生邊界問題、支集太短不利于信號能量集中。

實際應用中測井數據包含的信息非常豐富，且數據體比較大，不存在萬能模式。不同工作地區和地質條件不同，選擇的小波類型也必須通過該工作區典型鉆孔的小波分析結果與地質資料的反復對比來確定。目前已有較多的研究[7-8]使用測井曲線的小波變化進行沉積旋回的劃分。

Morlet小波不具有正交性的同時也不具有緊支集，其在時間-頻率域上分辨率很高，其實部和虛部之間的相位偏移為90°，可以方便地獲取信號的瞬時頻率和瞬時相位等信息[9-11]，在劃分沉積旋回時具有更好的適用性。

1.3 Morlet小波的改進

以Morlet為核函數的小波變換將時間域信號轉換到時間-尺度域時，需要通過基本小波的中心頻率和小波尺度這兩個參數來計算并獲取小波的中心頻率[12]，這將使小波參數的物理含義不能被清晰表達。

圖2 不同尺度參數下GR曲線的小波變換系數Fig.2 Wavelet transform coefficients of GR curve under different scale parameters

Morlet小波函數的基本公式為式(5)。

(5)

為了使小波基的參數選擇具有一定的自適應性，引入帶寬參數k2，提出以下的Morlet小波函數對信號進行小波變換：

(6)

將其代入公式(1)，得到

(7)

很明顯Morlet并不滿足小波的容許條件，因此也就不存在Morlet形式的重構公式或者逆變換公式。

當ω0≥5或者k2≥2時，上述積分值隨著或的增大而迅速減小，可忽略不計，此時Morlet函數接近滿足容許條件。據此，對式(6)進行了改進，取ω0=2π,得到改進后的小波函數：

(8)

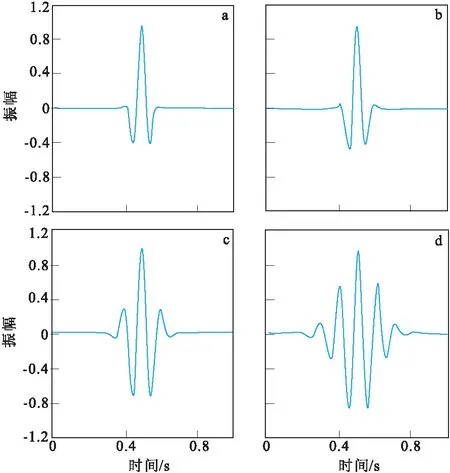
圖3 不同k2值Morlet小波波形Fig.3 Morlet wavelet waveforms with different k2 values(a)k2=1/4;(b)k2=1/3;(c)k2=1/2;(d)k2=1/1

分析Morlet小波發現，隨著值的增大，小波時域包絡線逐漸逼近余弦函數的某一段。小波時域持續期越長，頻率域小波濾波器帶寬越窄，抗噪性能越好，但增大值要受到容許條件和時域分辨率降低的限制，因此，對于Morlet小波而言，最佳的值需要根據具體情況來選擇。根據圖3中時域分辨率的表現以及多次測井數據試驗，本次設定值為1/2，既增強了有效信號的分辨率，又能避免振幅寬度過大影響臨近信號。

改進后的Morlet小波變換有以下幾個優點：①將信號從時間域映射到時間-頻率域；②小波各個參數有了明確的物理意義；③進行逆變換更加簡潔方便。

修改MATLAB小波分析工具箱Morlet小波基函數源代碼為：

function [out1,out2] = morlet(LB,UB,N,flagGUI)

out2 = linspace(LB,UB,N);

out1 = cos(-2*(out2.^2)) .* exp(2*pi*out2);

1.4 測井曲線的選擇

由于不同測井曲線會蘊含著不同的地質意義，若采用相同的函數和參數進行變換，可能會得到不同的結果。在研究中對GR、SP以及密度等多條測井曲線數據進行小波分析后發現，雖然得到的曲線形態上不一致，但對沉積周期的劃分基本一致(圖4)。

沉積巖地層中的自然伽馬曲線(GR)在高頻部分和低頻部分都包含有更豐富的信息，周期響應明顯，相對于密度曲線和自然電位曲線更能體現泥質含量的變化。利用其進行層序界面劃分與地層對比具有明顯的優勢，也是最有效的方法[13]。因此，筆者采用自然伽馬測井曲線進行分析。

2 小波信號的地質屬性

自然伽馬曲線的小波信號包含的2個地質屬性：砂/泥含量沿垂向的周期變化規律、頻率變化規律[14]。通過自然伽馬曲線的小波變換能夠快速-準確地獲得砂/泥含量和砂泥互層頻率，這是地層層序劃分的兩項重要指標，同時也是確定陸相盆地基準面旋回周期和劃分層序的重要依據。

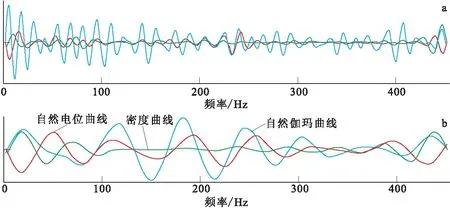
圖4 不同測井曲線的Morlet小波分析結果Fig.4 Results of Morlet wavelet analysis of different logging curves(a)高頻部分;(b)低頻部分

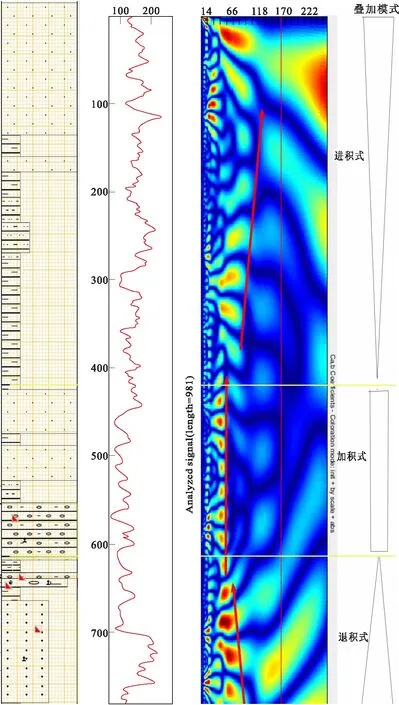
圖5 旋回疊加模式的GR曲線連續小波振幅譜分析Fig.5 Continuous wavelet amplitude spectrum analysis of GR curve of cyclic superposition model

利用Morlet小波基函數對自然伽馬測井信號進行1:1:256尺度小波連續分析，得到振幅圖譜(圖5)。在圖5中，能量的交替變化對應著砂泥巖互層沉積的變化。振幅譜能量的偏移方向對應著砂泥巖薄互層的厚度變化規律；能譜帶尺度的偏移對應著由凈沉積速率的變化引起的旋回逐漸增厚或減薄的變化。從下而上分析，能譜帶尺度偏小，表明相對水體上升，沉積速率減小、旋回厚度減小、砂/泥比變小，體現了退積式旋回的巖性變化特點，呈下粗上細正旋回；能譜帶尺度穩定，說明各旋回的厚度基本穩定、砂/泥比相同、體現了加積式旋回的巖性變化特點；譜帶尺度偏大，則反映了相對水體下降、沉積速率增加、旋回厚度增加、砂/泥比變大，很明顯的體現了進積式旋回的巖性變化特點，呈下細上粗反旋回。

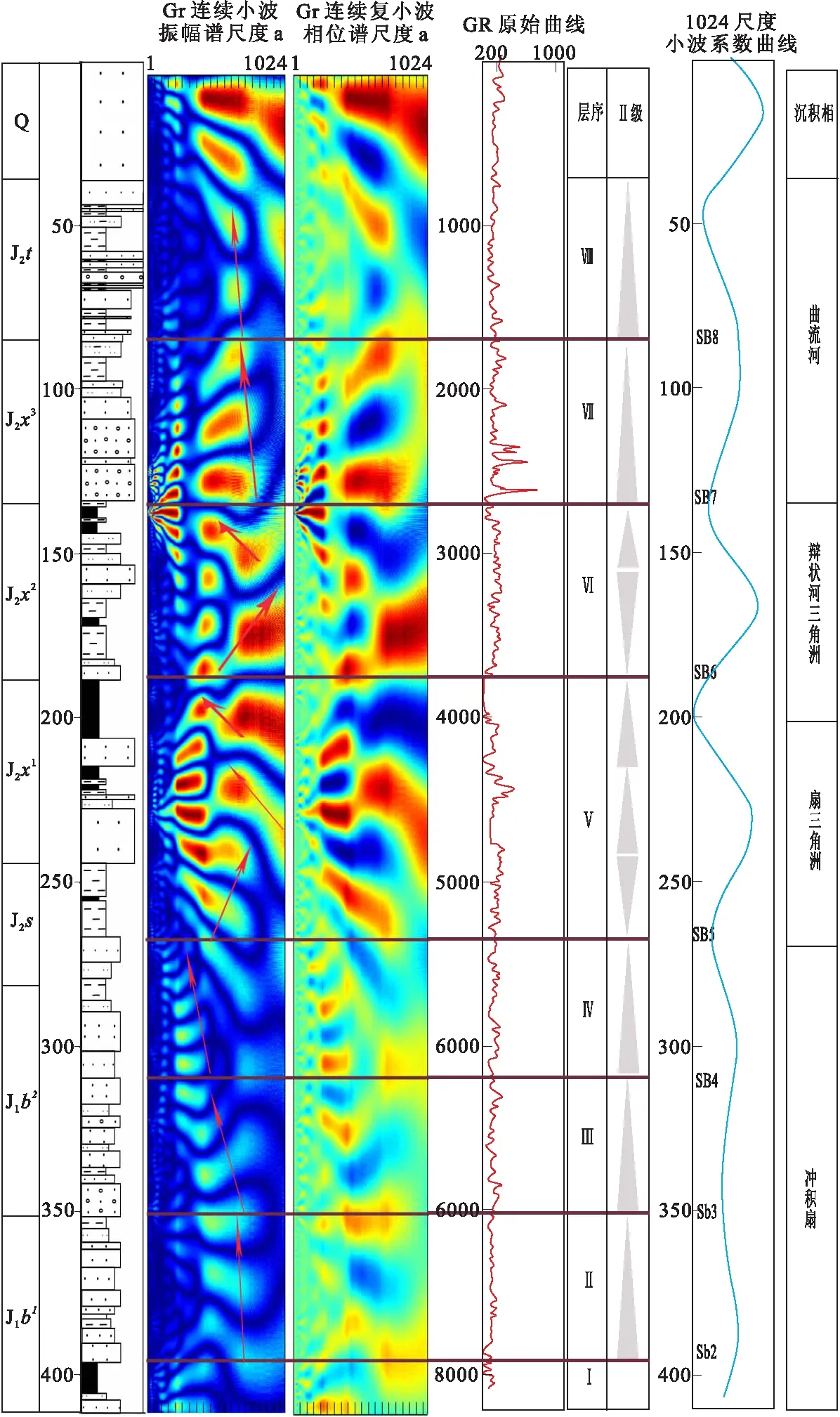
圖6 A4560孔Morlet一維連續小波振幅譜圖像Fig.6 Morlet one-dimensional continuous wavelet amplitude spectrum image of hole A4560

3 實際測井地層應用分析

3.1 區域地質概況

伊犁盆地南緣中下侏羅統水西溝群不整合上覆于三疊系，為一套在潮濕氣候條件下形成的、總體表現為退積特征的沖積扇-扇三角洲-曲流河沉積體系下形成的暗色含煤碎屑巖建造[15]。

該區地層較穩定，層理構造以水平層理為主，垂向充填序列的規律性周期變化，與基準面的波動是同一趨勢的。砂/泥比變化規律體現了三角洲的進退或者湖泊的擴張、收縮。

此次選取了最具代表性的蘇阿蘇地區A4560鉆孔侏羅系地層進行研究。

3.2 應用實例

3.2.1 小波分析結果

對自然伽馬曲線采用Morlet小波基進行一維連續小波分析，獲得了1:1:1024尺度小波振幅譜圖像(圖6)。

由于連續小波相位譜可以較好地識別層序級次及湖泛面位置，筆者對相位譜進行了計算并參考。

根據連續小波振幅譜和連續復小波相位譜劃分出劃分了7個層序界面(SB2-SB8)。

層序界面在相位譜上位于相位零點，不整合界面表現為彎曲的零線。振幅譜能譜帶位于界面上下存在突變現象，反映了沉積環境與沉積速率的變化。相轉換面的相位零線為直線形態，在振幅譜能譜帶上位于進積式旋回或退積式旋回的轉化處。

3.2.2 地質解釋

通過小波分析，在A4560孔劃分了8個不同疊加模式的旋回(Ⅰ～Ⅷ)，以退積式旋回為主，僅Ⅴ1、Ⅵ為進積式旋回:

八道灣組(J1b)地層分為上、下兩段，四個旋回(Ⅰ～Ⅳ)。每個旋回均由下部粗粒段(砂體)和上部細粒段組成，具有下粗上細的正韻律特征。其中下段兩個旋回(Ⅰ～Ⅱ)中，Ⅰ旋回發育有一層較厚的煤層，煤層下伏泥巖和細砂巖。Ⅱ旋回以粗砂巖占優勢夾有多層泥巖、粉砂巖，砂/泥比值較高，具有典型的沖積扇扇中特征。上段的Ⅲ旋回粗粒段以粗砂巖、砂礫巖為主，砂/泥比值最高，具有沖積扇扇根特征。Ⅳ旋回以粗砂巖為主，砂/泥比含量下降，頂部的泥巖和粉砂巖具有扇端特征。由此可看出，八道灣期基準面經歷了較長時期的上升過程。

三工河組(J1s)地層對應Ⅴ1亞旋回，巖性以泥巖為主，頂部覆蓋西山窯組的粗砂巖，無過渡沉積環境，呈斷陷湖盆扇三角洲常見進積型向上變粗的反韻律序列。

西山窯組下段(J2x1)地層以扇三角洲沉積為主，對應Ⅴ2亞旋回，扇中主體為粗砂巖和中砂巖，呈正韻律，基準面上升半旋回的頂部為扇端洼地，發育多組煤層。

西山窯組中段(J2x2)地層的巖性變化較為規律，巖性為粗、中砂巖-粉砂巖-泥巖-煤層，共兩組，對應Ⅵ旋回，包含一個完整的水退-水進周期，基準面下降半旋回時期略長于上升半旋回。巖性結構上，具有辮狀河沉積的假二元結構特征，其水平、波紋層理構造以及煤層的存在，說明該地層為濕潤氣候下的河漫沼澤沉積亞相。

西山窯組上段(J2x3)對應Ⅶ旋回，巖性由下向上為灰色含礫砂巖、砂巖、粉砂巖和泥巖，可分為四個沉積單元，砂/泥比接近1:1，基本上呈正韻律，韻律分為上下兩段，具有典型的二元結構特征，為曲流河相沉積。

頭屯河組(J2t)對應Ⅷ旋回，上伏于中侏羅統水西溝群，巖性主要為褐黃色、紫紅色的雜色碎屑巖沉積，其上部多為泥巖、中細砂巖互層，發育水平層理，底部以中粗粒砂巖為主，發育塊狀構造、交錯層理，可見薄煤層。該旋回曲流河沉積相和辮狀河沉積相特征均不明顯，暫劃分為曲流河相沉積。

3.3 結果對比

采用該方法流程對蘇阿蘇地區A4560、A4904、L29207、L34064孔進行了層序劃分，與地質報告中的劃分結果對比見表1。

表1 各鉆孔層序劃分結果對比Tab.1 Comparison of sequence division results of each borehole

通過表1可以看出，利用該方法劃分的層序與巖性巖相+電性分析法劃分的層序基本相同，除A4560、A4904孔在Ⅳ、Ⅴ旋回界面略有差別，其余界面基本吻合。

4 結論

在傳統Morlet小波變換的基礎上，引入參數對帶寬進行控制，使得小波函數的表達形式更加靈活，在物理學和地質學上的意義表達更清晰。

利用改進的Morlet小波變換，對自然伽馬測井曲線進行連續小波振幅譜和復小波相位譜特征分析，實現周期級別、旋回類型、層序界面的識別和劃分，對于不同類型的層序界面，其振幅譜和相位譜響應特征有明顯區別。與傳統的地層層序劃分手段相比，該方法能更加有效地利用自然伽馬測井數據的內部結構信息，準確的識別層序界面，為層序劃分提供更加可靠的依據。