基于向量旋轉的擬合空間圓方法研究

張振虎

上海勘察設計研究院（集團）有限公司 上海 200082

引言

隨著科技的發展、信息技術的進步，以及精密工程技術的發展，產生了很多新的測量技術，三維測量建模技術就是時代的產物。在核電廠、光源儲存環、離子加速器實驗裝置等項目建造過程中，三維設計、設備制造、核心設備精密安裝及重要設備在線監測均進行了大量建模，建模技術的采用促使高精度測量工作日益轉向可視化、智能化及精密化。逆向建模作為一種最常用的建模方法得到了越來越廣泛的應用，它主要通過激光掃描、激光跟蹤或攝影測量等技術，獲得目標物體的三維測量數據，然后根據測量數據構建三維高精度模型。以核電廠為例，其在建造過程中采用了激光跟蹤技術對一回路主要設備，如反應堆壓力容器、蒸汽發生器、主泵、主管道及波動管等進行了精密建模，這些設備的接口多為圓形，而這些設備接口的圓形并不在嚴格的水平面上，因此，對這些設備建模通常需要對空間圓進行擬合。

1 數學模型及算法

空間圓無直接公式描述，基于公式擬合的方法很難實施，故空間圓參數擬合一般采取間接方式進行。根據參考文獻[1-5]，擬合空間圓主要采用平面與圓球相截法。由圓球性質可以得知，任何一個平面與圓球相截得到的截面均為圓形，故平面與圓球相截法是通過擬合平面與圓球得到空間圓參數。其中，文獻[1-4]采取擬合平面和一個圓球中心位于擬合平面上的圓球得到空間圓參數；文獻[5]也采取擬合平面和圓球方式進行，該方法不要求圓球圓心位于擬合平面上，在平面和圓球擬合后將球心投影到擬合平面上以得到圓心，過程較文獻[1-4]復雜。擬合空間圓需要確定7個參數，包括空間圓所在平面的法向量(a，b， c)、空間圓的圓心(x0， y0， z0)和空間圓的半徑R。本文通過擬合平面求取平面法向量，構建旋轉矩陣，然后將空間圓擬合問題轉化為平面圓擬合問題。在工程實例中，圓形截面的特征數據采集通常采用全站儀、激光掃描儀或激光跟蹤儀完成。部分物體圓形截面因受視線阻隔往往難以一次測量就采集到所有特征數據，通常需要轉站1～2次完成。轉站需要進行大角度坐標轉換，故在擬合空間圓前需要將多站的采集數據轉換到同一個坐標系中。

綜上，本文算法主要分為以下五步：①大角度坐標轉換；②擬合空間圓所在平面求取平面法向量；③根據平面法向量構建旋轉矩陣；④將擬合坐標點旋轉，求取平面圓圓心和半徑；⑤平面圓圓心旋轉得到空間圓圓心。

1.1 大角度坐標轉換

坐標轉換模型可表示為：

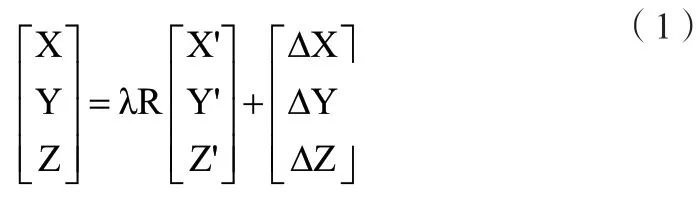
其中，（X'、Y'、Z'）為轉換前坐標，（X、Y、Z）為轉換后坐標，λ為尺度系數，R為含三個旋轉角α、β、γ的旋轉矩陣，△X、△Y、△Z為平移參數。R=RxRyRz，Rx是把原坐標繞X軸旋轉α角得到的旋轉矩陣，Ry是把原坐標繞Y軸旋轉β角得到的旋轉矩陣，Rz是把原坐標繞Z軸旋轉γ角得到的旋轉矩陣，α、β、γ均為繞軸逆時針旋轉。

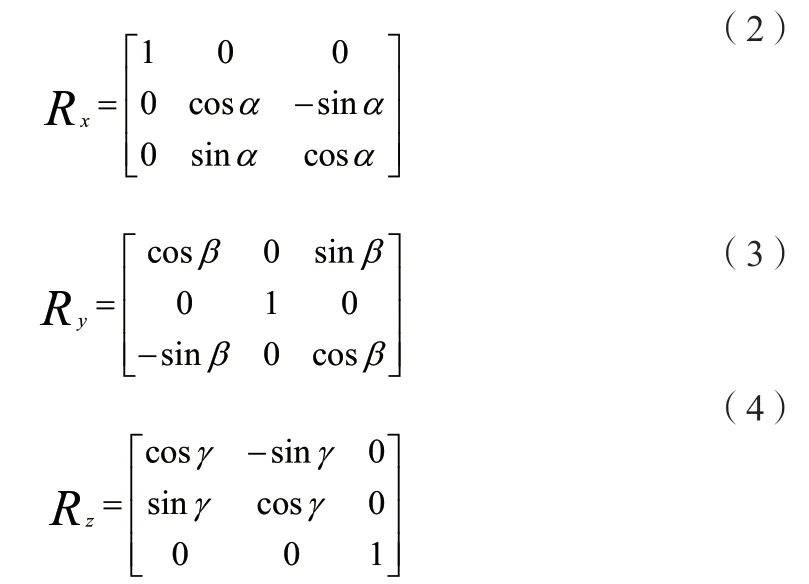
整理以后，旋轉矩陣R為以下形式：

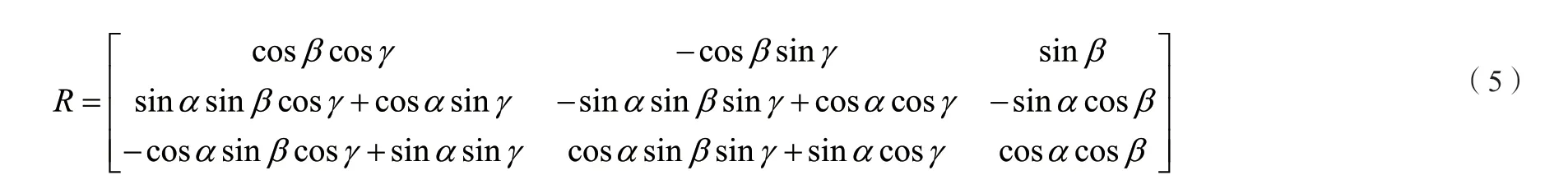
兩坐標系之間轉換需要求取7個轉換參數，一般需要三個以上的公共點坐標來進行轉換。

為便于數據處理，一般需要對所使用的公共點坐標進行重心化處理，將兩套坐標系的坐標均轉化為重心化坐標。根據參考文獻[8]，重心化坐標計算公式如下：

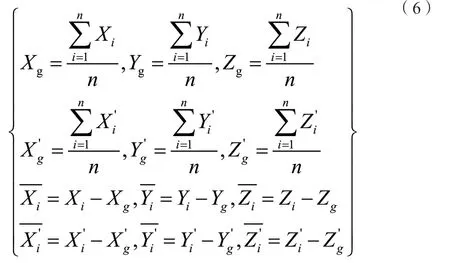
將公共點的中心化坐標代入式（1），可得：

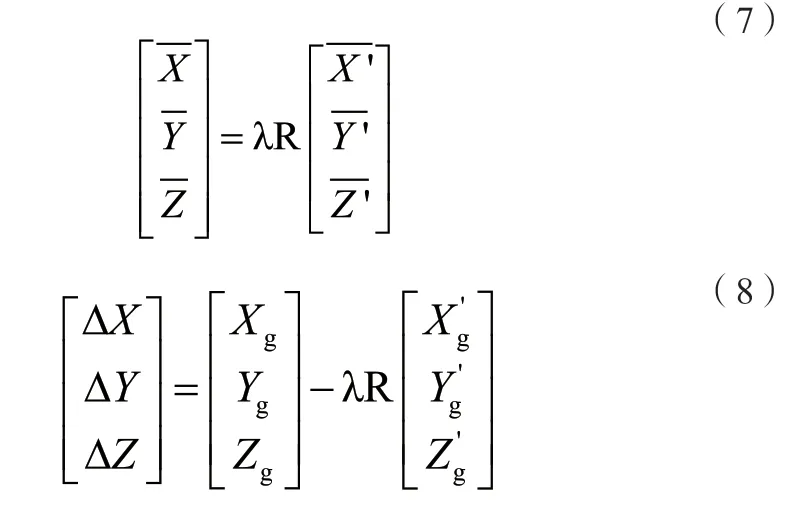
從上式可以看出，坐標轉換參數計算時需要先計算尺度系數和旋轉矩陣，然后代入式（8）就可以得到平移參數。

根據參考文獻[9]，對式（7）兩邊取2-范數，由于R為正交矩陣，及λ＞0，可得

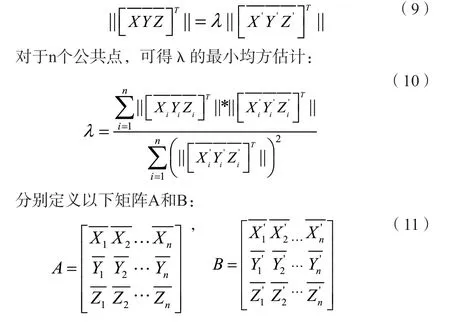
式（7）變化為以下形式：

求取正交矩陣R，使A-λRB的Frobenius范數最小時所得的R即為最佳轉換矩陣，即求解以下問題：

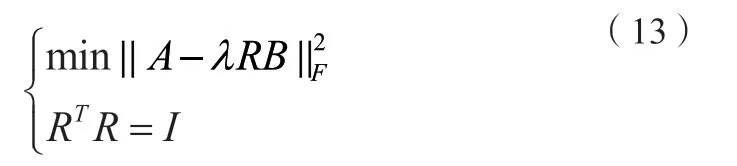
將上式進行跡函數計算并展開，得：

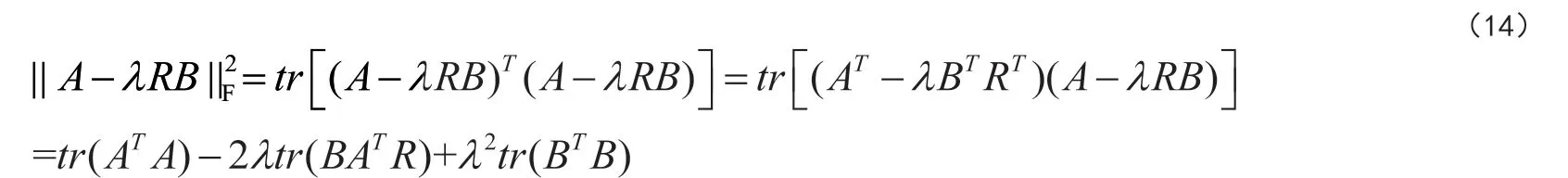
根據參考文獻[6]，當且僅當R =VUT時，式（14）得到極小值。得到旋轉矩陣后，將旋轉矩陣代入到公式（8），就可以得到平移參數。

1.2 平面法向量計算

將所有坐標采集數據轉換至同一坐標系后，就可以開始計算空間圓所在平面的法向量計算。

平面方程一般可表示為：

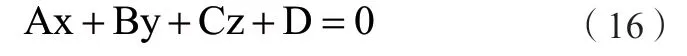
為減少參數的計算，可以將方程簡化，兩側同除以D（D≠0），方程可以簡化為：

因方程的三個參數之間存在著線性關系，故可以采用求解線性方程組參數的方法進行結算。假設空間圓上的n個觀測點為( xi， yi， zi)（1≤i≤n），以矩陣形式表示如下：

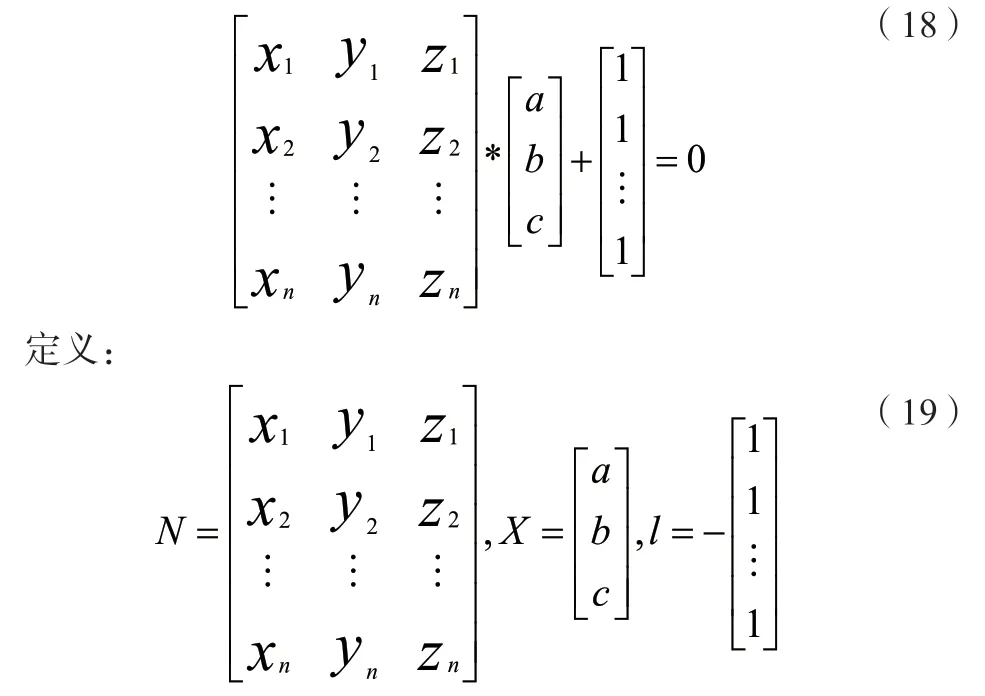
上式可以簡化為：

其最小二乘解為：

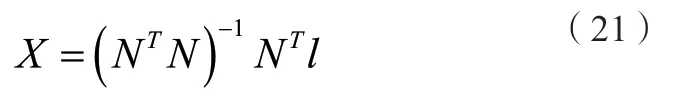
上述算法為擬合平面最常用算法，但該算法并未考慮系數矩陣N 中存在的誤差，且造成了固定項l 中數據的改動，得到的結果必然不是最優的。

假設系數矩陣N中存在獨立同分布誤差，根據參考文獻[6]，其參數求解可以采用以下算法。

將( xi， yi， zi)重心化，得到重心坐標重心化公式如下：

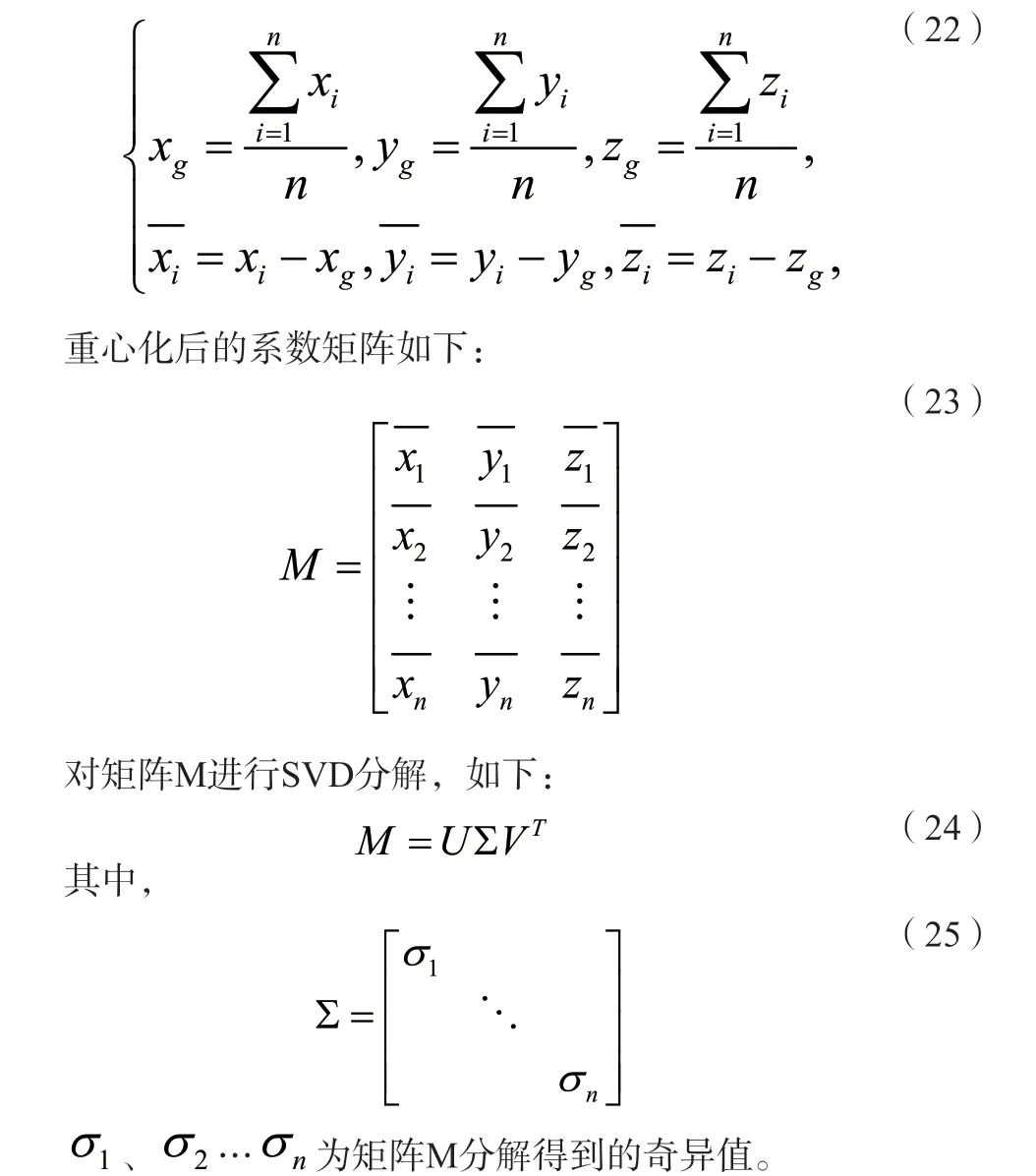
最小奇異值所對應的V向量[ a 'b ' c ']T即為平面方程中參數A、B、C的值。平面方程中常數項的值可按下式計算：

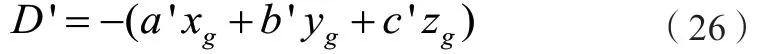
根據文獻[7]研究，基于奇異值分解的擬合平面方法與基于正交距離擬合平面的方法是等價的，其求得的平面參數可以使點到平面的距離平方和最小，其比式(18)—(21)采用的擬合平面常用算法更為精確。

1.3 求取圓心和半徑

（1）構建旋轉矩陣

假設空間圓的圓心坐標為( x0， y0， z0)，其應位于擬合的平面上，故有：

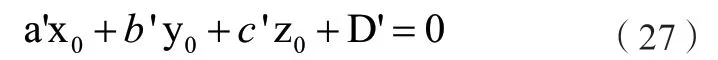
應用羅德里格旋轉公式矩陣形式，將平面法向量旋轉至與Z軸平行，其構成的旋轉矩陣如下：

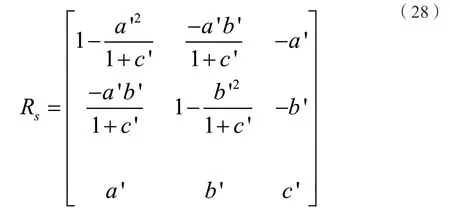
其旋轉公式表達為：

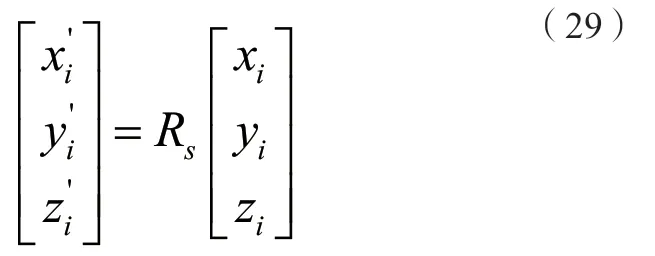
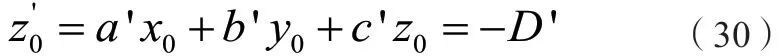
（2）擬合平面圓

平面圓方程可以用下式表示：

采用最小二乘法可以得到E、F、G的值，平面圓圓心及半徑值計算如下：

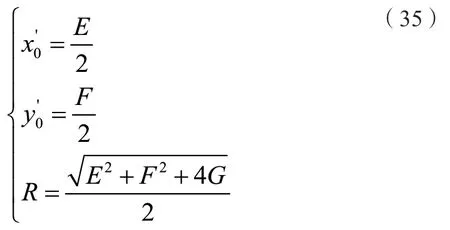
（3）解算空間圓圓心

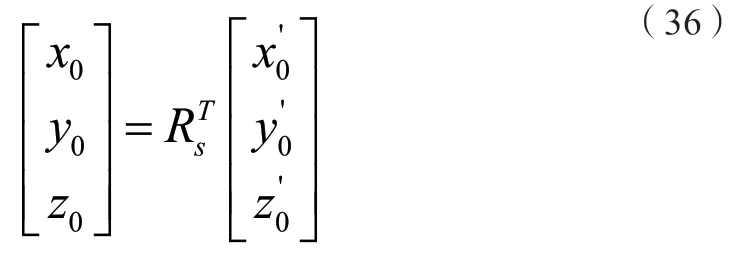
1.4 擬合空間圓效果評價

計算擬合點到空間圓的法向偏差：

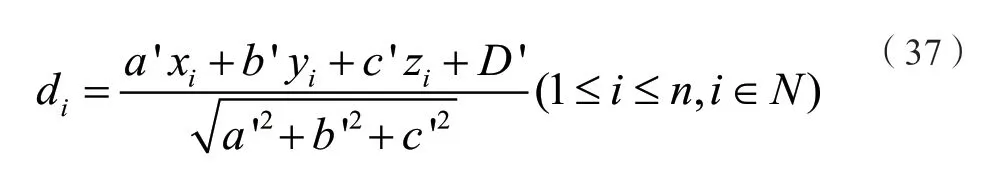
計算擬合點到擬合圓的徑向偏差：

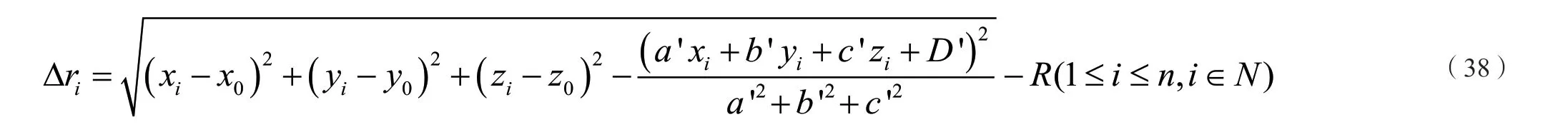
計算擬合點到擬合圓的空間偏差：

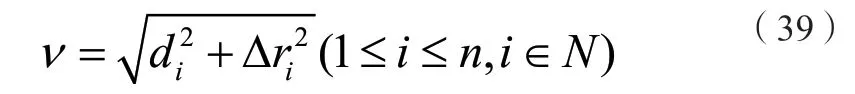
計算RMSE（均方根誤差）：

2 工程算例

某設備中部的法蘭需要與其他設備法蘭進行精密對接，為檢測設備的匹配性，需要在安裝前進行模擬對接。為精確模擬，采用激光跟蹤儀對設備的法蘭圓面進行了測量。因視線阻擋，難以在一站就完成所有數據的采集，故法蘭圓面的測量采取了轉站測量的方式，兩站之間采用公共點進行連接。采集的原始數據請見下表1。

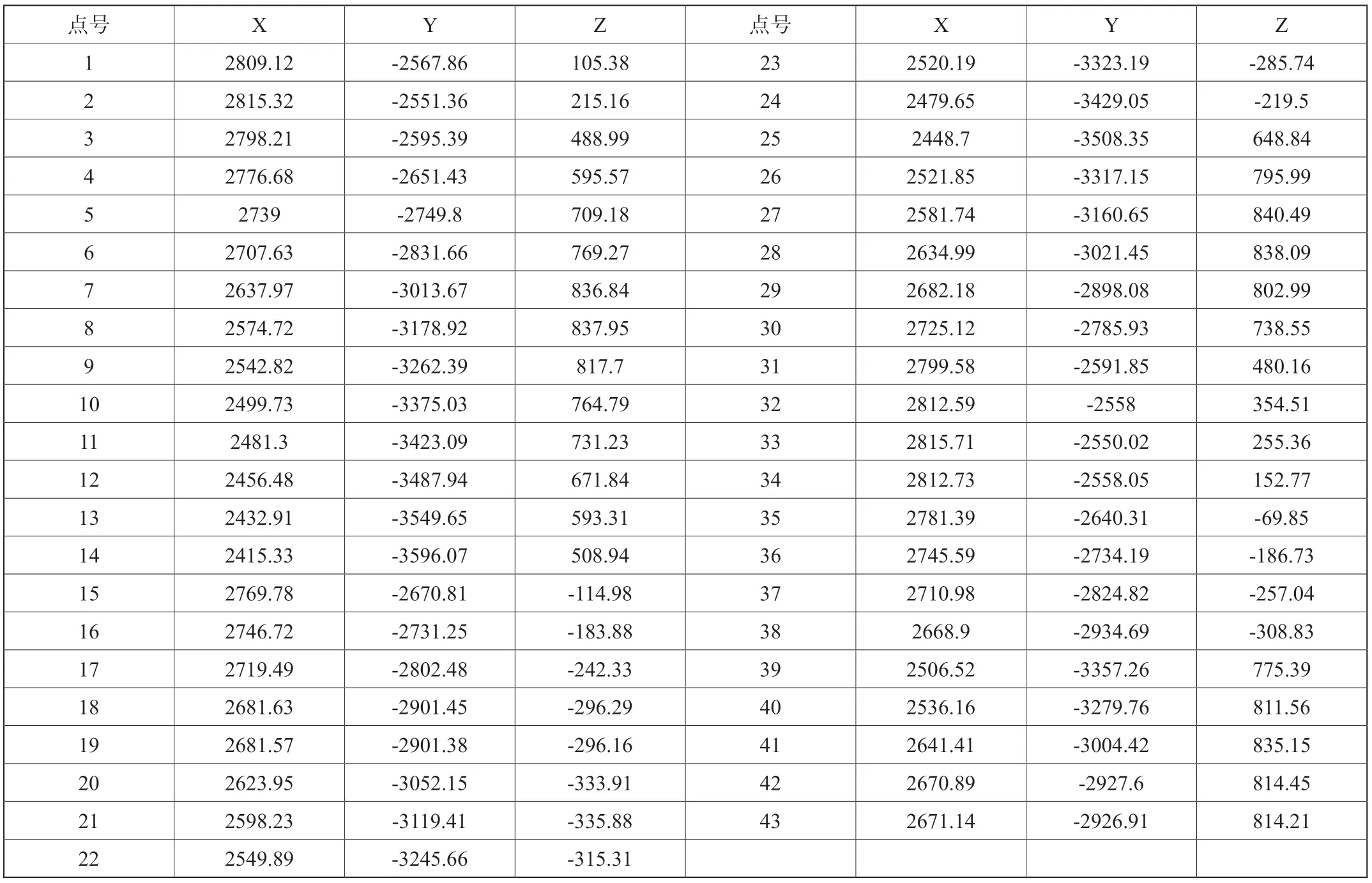
表1 某設備中部法蘭圓第一站測量數據（單位：mm）

表2 某設備中部法蘭圓第二站測量數據（單位：mm）

表3 公共點測量數據（單位：mm）

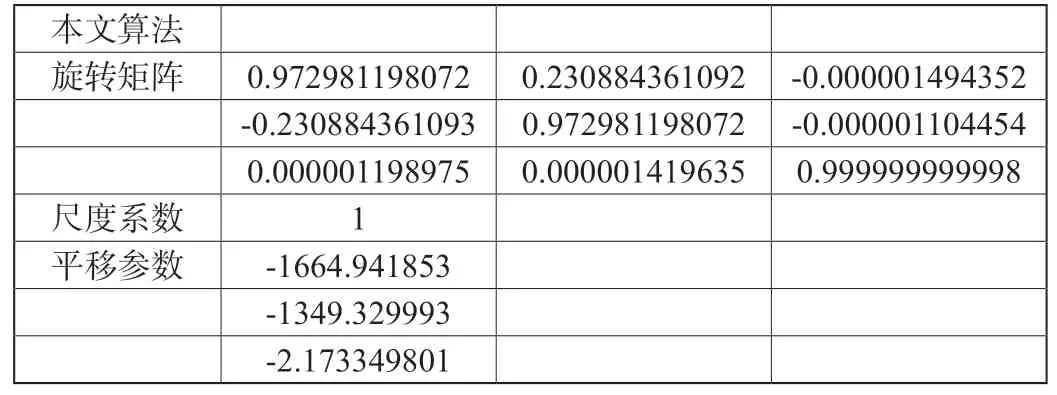
表4 坐標轉換參數

采用本文坐標轉換算法，計算第二站轉入第一站的坐標轉換參數。因激光跟蹤儀的精度很高，且測量距離較短，其坐標轉換尺度系數可視為1。計算出來的旋轉矩陣及平移參數請見表4。

利用表4的坐標轉換參數將第二站的測量數據轉入到第一站測量坐標系中，并計算擬合圓的參數。根據本文算法，對空間圓的數據進行了擬合，擬合后的平面方程單位法向量為（0.93393557，-0.357440912，0.000587606），平面方程常數項為-3541.36949，空間圓圓心坐標為（2605.2329，-3100.094608，253.8655206），半徑為589.6816919mm。根據擬合結果計算出的擬合后各點的法向偏差、徑向偏差及空間偏差見表5。

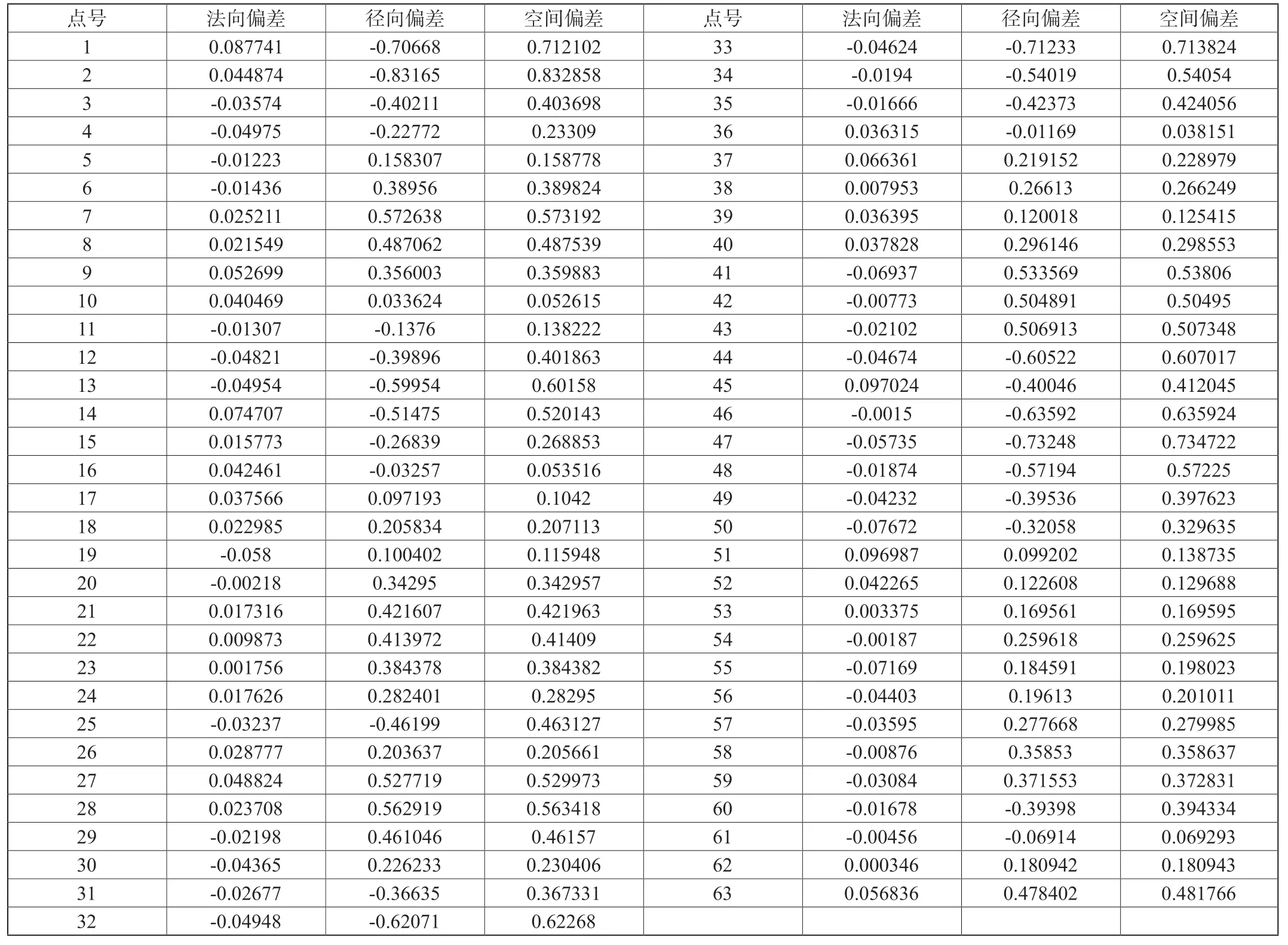
表5 某設備端面圓擬合后偏差統計（單位：mm）

采用式(40)，根據表5中所示的各點的法向偏差、徑向偏差及空間偏差計算均方根誤差（RMSE）。經計算，法向偏差RMSE為0.042167mm，徑向偏差RMSE為0.409195mm，空間偏差RMSE為0.411362mm，說明擬合圓的各項偏差均很小，空間圓參數解算較準確。

為驗證本文中算法，使用文獻[2]中的算法對本文數據進行擬合。為便于擬合后參數的對比，本文將采用文獻[2]中算法解算出的平面法向量進行了單位化。文獻[2]中算法和本文算法解算的結果如表6所示。

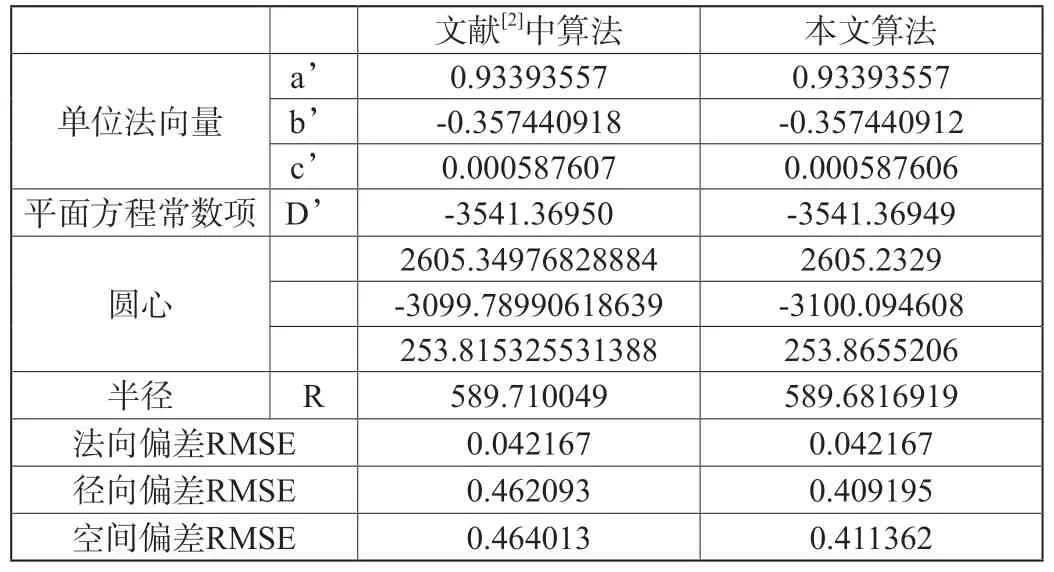
表6 文獻[2]算法和本文算法解算結果（單位：mm）

通過表6可發現，本文所述算法擬合空間圓后法向偏差RMSE和文獻[2]中使用的算法結果基本一致，但徑向偏差RMSE及空間偏差RMSE均略優于文獻[2]中使用的算法，說明本文算法可行，精度較高。

3 結束語

本文通過奇異值分解法擬合平面，構建旋轉矩陣化空間圓擬合為平面圓擬合，原理清晰，不用進行迭代，且有利于編程計算，并通過實踐證實，該方法實用且可靠。適合用于核電廠、光源存儲環實驗裝置、直線加速器實驗裝置、飛機、造船、汽車、航空航天等行業大型設備模型構建過程中圓形截面的擬合。