基于運動檢測的飛行區車輛差分北斗/ SINS組合導航

胡 杰 王子卉 朱倚嫻

1 中國電子科技集團公司第二十八研究所空中交通管理系統與技術國家重點實驗室，南京市永智路1號，210014 2 東南大學微慣性儀表與先進導航技術教育部重點實驗室，南京市四牌樓2號，210096 3 南通大學機械工程學院，江蘇省南通市嗇園路9號，226019

建立飛行區車輛管控系統有利于實現車輛的可視化、數字化、精細化管理[1]，車載定位系統能夠實時準確地提供車輛行駛態勢，是實現車輛監控管理的前提。在車載定位系統中組合使用捷聯慣導系統(SINS)與全球衛星導航系統(GNSS)，可以獲得車輛行駛速度、位置以及姿態等信息[2-3]。我國北斗導航系統已完成全球組網，正在推進其在民航領域的應用，差分北斗與SINS融合可為飛行區車輛管控系統提供高精度的位置服務。

當衛星信號有效時，SINS與GNSS融合能夠獲得車輛的行駛速度、位置等參數；當衛星信號受到遮擋時，組合導航系統精度會降低。劉鵬飛[4]提出一種里程計(DR)輔助的高精度GNSS/INS組合導航方法，并建立了GNSS/INS和DR/INS兩種組合導航濾波模型，可根據車輛行駛環境切換濾波模式，具有長時間、高精度導航定位功能，但需要安裝輔助導航設備，因此使用范圍受限。張夢得等[5]針對GPS短時失效的問題提出一種基于偏最小二乘輔助高斯過程回歸的SINS/GPS組合導航方法，但該方法的適用性還需進一步驗證。Yao等[6]和張倫東等[7]提出一種基于零速修正技術(ZUPT)的組合導航方法，利用車輛停止或行人駐足時速度為0作為約束條件來估計SINS誤差。胡杰等[8]提出利用車輛行駛中側向和天向速度為0構造濾波器量測約束信息，稱為動態零速修正技術(DZUPT)，但當車輛急速轉彎時，側向速度為0的假設條件不成立。周俊等[9]對GNSS/SINS組合導航算法進行研究，但未考慮衛星失效時引起系統精度降低的問題。近年來，部分學者[10-11]提出利用機器學習、深度學習等技術輔助SINS導航，但這些算法實現較為復雜，在使用中存在局限性。

本文針對飛行區車輛衛星信號斷續或遮擋時導航系統精度降低的問題，利用ZUPT與DZUPT結合的運動學約束技術，提出一種基于車輛運動檢測的差分北斗/SINS組合導航方法。針對車輛行駛特征給出組合導航系統框架，建立組合導航濾波狀態方程與量測方程，根據SINS輸出信息實現車輛運動狀態的檢測，并對該方法進行實驗驗證。

1 基于運動檢測的差分北斗/SINS組合導航系統框架

圖1為本文提出的飛行區車輛差分北斗/SINS組合導航系統框架。當北斗衛星信號有效時，組合導航濾波器利用差分北斗提供的速度、位置信息作為觀測量進行濾波器量測更新，并根據估計得到的誤差值反饋校正SINS。當北斗衛星信號受到遮擋時，要利用SINS提供的導航信息，首先需通過車輛運動狀態檢測模塊來判斷當前的車輛行駛狀態(停車狀態、直線行駛或拐彎行駛)；然后根據車輛運動學特性構造相應的運動約束信息(ZUPT模式、DZUPT模式或僅時間更新的DZUPT模式)；最后將構造得到的運動學約束輔助信息與SINS相組合，實現系統的誤差估計與校正。

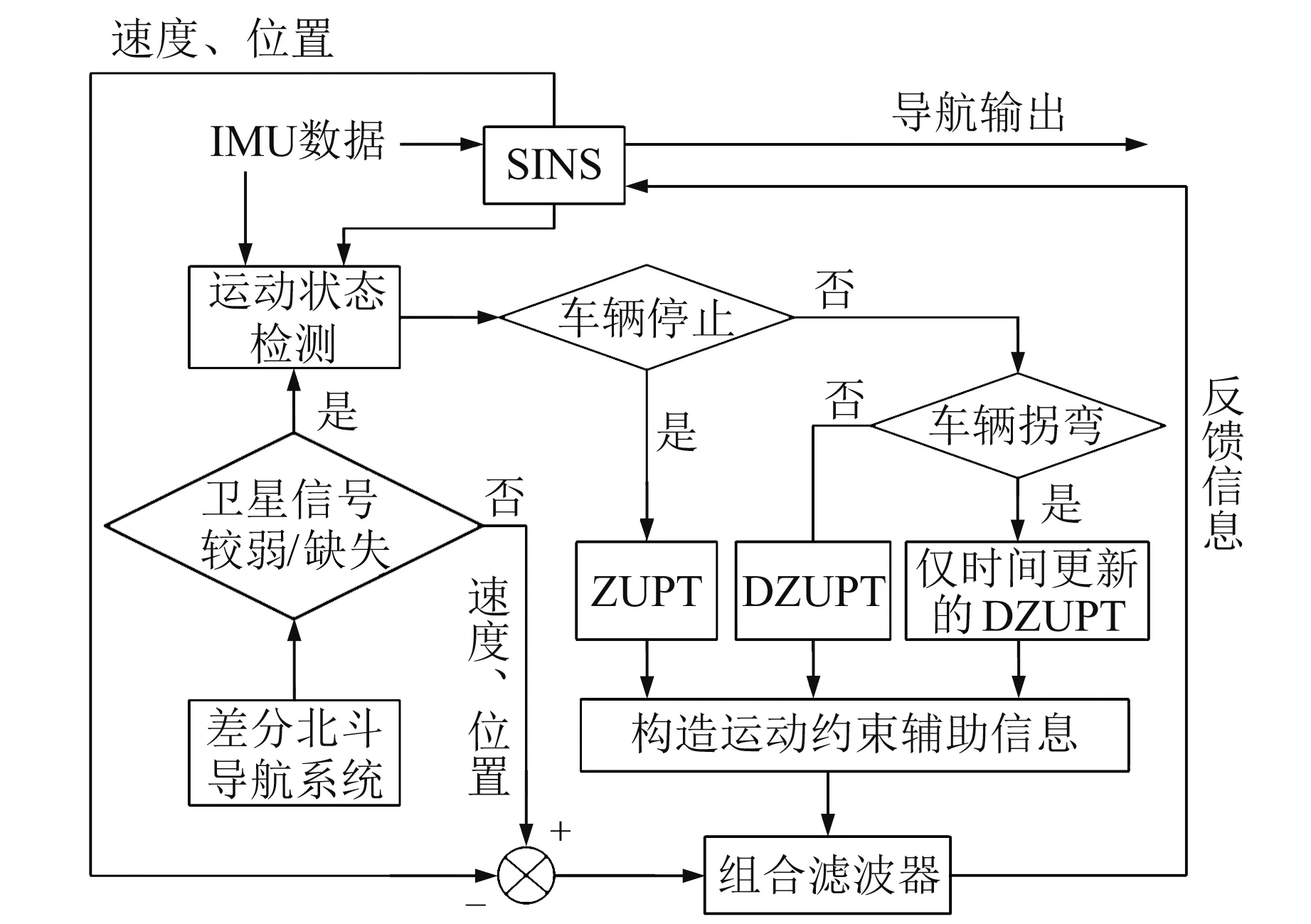
圖1 組合導航系統框架Fig.1 Frame of integrated navigation system

2 組合導航濾波器設計

本文導航坐標系選取東-北-天地理坐標系，記為n系，慣性坐標系記為i系，載體坐標系記為b系，其中oxb軸沿車體橫軸指向右方，oyb軸沿車體縱軸指向前方，ozb軸垂直于車體向上，即構成一個右-前-上坐標系。

2.1 系統狀態方程

X=[δLδλδhδvEδvNδvU

φEφNφUεxεyεzxyz]T

(1)

進一步，由SINS誤差方程可得到組合導航濾波狀態方程為：

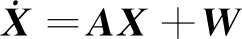
(2)

式中，A為系統狀態轉移矩陣，可根據SINS誤差確定；W為系統噪聲向量。

2.2 系統量測方程

2.2.1 北斗衛星信號有效時

當衛星信號有效時，將SINS輸出速度、位置與北斗接收機輸出速度、位置的差值作為Kalman濾波器測量值，此時濾波量測方程可表示為：

Z1=H1X+V1

(3)

式中，Z1為衛星信號有效時的量測向量；V1為系統量測噪聲向量；H1為量測矩陣，可表示為：

(4)

式中，I3×3表示3×3維單位矩陣；03×3、03×9分別表示3×3和3×9維零矩陣。

2.2.2 北斗衛星信號失效時

當衛星信號失效且檢測到車輛處于停止狀態，即組合導航系統處于ZUPT模式時，利用車輛n系3個方向速度為0的特性構造濾波器量測值：

(5)

式中，Z2為衛星信號失效且車輛停止時的量測向量；vE、vN和vU分別為n系3個方向的速度誤差；vE、vN和vU分別為n系3個方向的速度值。

由式(5)可得到衛星信號失效且車輛處于停止狀態時的量測方程為：

Z2=H2X+V2

(6)

式中，V2為系統量測噪聲向量；H2為量測矩陣，可表示為：

(7)

當衛星信號失效且車輛處于直線行駛，即組合導航系統處于DZUPT模式時，利用車輛運動學特性約束SINS誤差。假設車輛無側滑、跳躍等運動，則b系中側向和天向速度可近似為0，如圖2所示，該方法被稱為非完整性約束[12]。

圖2 非完整性約束Fig.2 Non-holonomic constraint

(8)

式中，vb、vn分別為b系和n系車輛速度。由式(8)可得b系速度誤差表達式為：

(9)

式(9)可進一步表示為：

δvb=Hv,1δvn+Hv,2φn

(10)

其中，

(11)

(12)

利用車輛非完整性約束條件可構造濾波器量測值為：

(13)

由式(10)和式(13)可得量測方程為：

Z3=H3X+V3

(14)

式中，V3為系統量測噪聲向量；H3為系統量測矩陣，可表示為：

H3=

(15)

式中，Hv,1(1,)、Hv,2(1,)表示矩陣第1行；Hv,1(3,)、Hv,2(3,)表示矩陣第3行；01×3表示1×3維零矩陣。

3 運動狀態檢測

根據分析可知，車輛狀態可分為直線行駛、拐彎行駛和停止3種。當車輛停止時，可采用傳統ZUPT進行誤差約束；當車輛直線行駛時，利用車體側向和天向速度為0進行非完整性約束；當車輛急速拐彎時，會產生較大的向心加速度，車體側向和天向存在速度分量，不滿足DZUPT約束條件，但一般情況下車輛拐彎時間較短，此時Kalman濾波算法需暫停量測更新，即組合導航系統處于僅時間更新的DZUPT模式。

假設k時刻IMU輸出的車輛角速度和比力分別為ωk=[ωxkωykωzk]T、fk=[fxkfykfzk]T，車輛運動狀態檢測的目的是根據IMU輸出的信息確定當前車輛行駛狀態，具體實現過程如下：

1)確定停止狀態閾值。在車輛初始對準階段，采集3～5 min的IMU原始靜態數據計算角速度和加速度檢測閾值，表達式為：

(16)

式中，λG和λA分別為車輛停止時陀螺和加速度計的檢測閾值；N為數據采集時間長度；ωi和fi(i=1, 2,…,N)分別為時間窗內i時刻IMU輸出的陀螺和加速度計值；‖·‖表示2范數。

2)判別車輛是否停止。滑動窗口時間取值為T，根據IMU采樣頻率可求得T時間段內采樣值，假設為M。實時計算滑動窗口內角速度和比力平均值，并與式(16)進行比較，以此來判斷車輛是否停止：

(17)

(18)

式中，LG(·)和LA(·)分別為根據陀螺和加速度計輸出求得的車輛停止檢驗值；g為當地重力加速度。判斷車輛是否停止可認為是假設檢驗問題，當式(19)成立時，車輛即可被認為處于停止狀態：

(19)

3)判別車輛是否拐彎。由牛頓運動定律可確定車輛向心加速度為：

a(t)=V(t)×ωz(t)

(20)

式中，a(t)為t時刻車輛向心加速度；V(t)為車輛行駛速度；ωz(t)為陀螺輸出沿垂向拐彎角速度。

如果|a(t)|≥λa，說明車體急速拐彎，此時將誤差約束切換至僅時間更新的DZUPT模式，其中檢測閾值λa由車輛實際行駛路況及車輛拐彎幅度確定。

4 車載實驗

車載驗證實驗裝置由差分北斗/MEMS SINS組合導航系統、北斗差分基準站、北斗接收天線等組成，SINS中采用的MEMS陀螺儀零偏穩定性(1 s平滑，1σ，室溫)優于5°/h，加速度計零偏穩定性(1 s平滑，1σ，室溫)優于100 μg。采用高精度Septentrio PolaRx5型GNSS接收機保存的星歷和觀測數據進行事后RTK差分處理，獲得車輛參考行駛路線，數據更新頻率為1 Hz，位置精度優于0.05 m。

實驗地點為某機場飛行區，利用專用移動通信網絡實現北斗差分站與行駛車輛以及行駛車輛與監控席位之間的數字通信。圖3為車輛行駛軌跡，圖4為該時間段內北斗可見衛星個數及其幾何精度因子曲線(GDOP)，圖5為差分北斗/SINS組合導航系統位置誤差曲線，表1為位置誤差統計結果。

圖3 車輛行駛軌跡Fig.3 Vehicle track

圖4 可見衛星個數及其GDOPFig.4 Numbers of visible satellites and their GDOP

圖5 差分北斗/SINS組合導航位置誤差Fig.5 Position errors of differential Beidou/SINS integrated navigation

表1 組合導航位置誤差數值統計

由圖4可以看出，該時間段內可見衛星個數最少為14顆，最多為16顆，滿足差分定位需求；GDOP最大值為2.35，衛星幾何分布優。由圖5及表1可以看出，組合導航系統的最大位置誤差小于1 m，表明差分北斗與SINS組合后能夠為飛行區車輛管控系統提供亞米級精度位置服務。

為進一步模擬車輛在機場停機坪、廊橋等遮擋環境下的組合導航系統定位精度，利用保存的SINS和差分北斗數據，通過人為切斷北斗接收機的衛星信號對本文提出的基于運動檢測的DZUPT約束組合導航方法進行驗證。行駛里程約為2.5 km，時刻為605～919 s，對應圖3中A-B行駛路段。該路段車輛行駛狀態包括直線行駛、停車以及拐彎行駛等，傳統DZUPT約束與本文提出的基于運動檢測的DZUPT約束的位置誤差對比曲線如圖6所示，表2為2種約束方法的最大位置誤差對比統計。

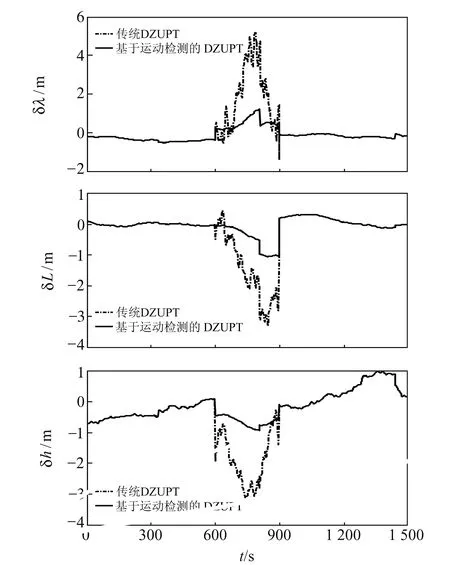
圖6 衛星信號失效時組合導航位置誤差對比Fig.6 Comparison of position errors of integrated navigation under the satellite signal outage

表2 衛星信號失效時組合導航的最大位置誤差對比

由圖6及表2可以看出，當中斷衛星信號并采用傳統DZUPT約束輔助時，組合導航系統的經度誤差最大為5.21 m，引起誤差的主要原因為拐彎時車輛側向速度不為0，傳統DZUPT的約束條件不成立；當采用本文提出的基于運動檢測的DZUPT約束輔助時，通過運動狀態檢測算法能夠實時檢測車輛的運動狀態，當車輛拐彎時則切換濾波器至僅時間更新的DZUPT模式，可隔離車輛拐彎所引起的量測誤差，經度最大誤差減小為1.35 m，從而提高了組合導航系統精度。

5 結 語

為進一步提高機場飛行區車輛組合導航精度，本文對北斗導航系統衛星信號中斷時SINS位置誤差隨時間積累問題進行分析和研究。提出一種基于運動檢測的DZUPT輔助約束SINS組合導航方法，當衛星信號中斷時，利用慣性測量單元輸出的陀螺和加速度計信息以及SINS輸出的車輛速度來實現運動狀態在線檢測，從而切換組合導航系統至對應的輔助約束模式。

車載組合導航驗證實驗結果表明，當北斗導航系統衛星信號有效時，差分北斗與SINS組合定位精度優于1 m；當衛星信號中斷時，本文提出的基于運動檢測的DZUPT輔助約束方法相比于傳統DZUPT約束方法定位精度更高。