新西蘭海潮負荷位移建模精度分析

劉中冠 袁林果 陳昌福 成 帥 張 迪

1 西南交通大學地球科學與環境工程學院，成都市高新區西部園區，611756

利用GPS技術反演海潮負荷位移參數主要分為靜態方法和動態方法。例如吳志露等[1]利用傅里葉變換從動態PPP解算的時間序列中提取出潮波參數，解算結果證明了GPS反演有效、可靠，然而其解算過程中忽略了時間序列長度以及地心運動改正對潮波參數的影響；魏國光等[2]證明，短期靜態PPP解算結果中提取的潮波參數可用于補充觀測資料的不足，但由于其靜態PPP解算精度為cm級，因而該結論還有待論證。上述研究主要利用不同海潮模型進行對比分析，而在當前GPS觀測精度下，有必要分析不同地球模型對海潮負荷位移參數的影響。

本文使用靜態方法，利用新西蘭南北島陸地范圍內189個GPS測站連續11 a(2008～2018年)的觀測數據解算8個主要潮波的位移參數，并選取7種全球海潮模型與GPS反演結果進行對比，分析4種地球模型對海潮負荷位移參數的影響，最后對GPS實測結果和模型值之間的殘差進行初步探討。

1 研究區域

新西蘭地處南半球中緯度地區，位于太平洋和印度-澳大利亞板塊的交界處，其四周海域寬廣、潮汐負荷效應明顯，是全球范圍內海潮負荷位移較大的區域之一。圖1為研究范圍內陸地部分8個主要潮波(M2、S2、N2、K2、K1、O1、P1和Q1)海潮負荷位移的疊加，由于不同潮波不可能同時處于最大值，因此實際最大振幅小于此結果。由圖可知，在垂直方向上，新西蘭北島北部區域由海潮負荷引起的形變超過50 mm，南島東部海潮負荷位移值僅10 mm，海潮負荷位移南北差異明顯；水平方向負荷位移較小，最大值理論上不超過15 mm。

圖1 新西蘭地區海潮負荷位移Fig.1 The ocean tidal loading (OTL) displacement in New Zealand

2 研究方法及數據處理

2.1 靜態方法解算海潮負荷位移參數原理

根據IERS2010規范[3]，并考慮周期為18.6 a的節點調制影響，測站的海潮負荷瞬時位移公式可表示為：

(1)

式中，k為站心地平坐標系中的東、北及垂直方向，j為11個潮波(4個半日潮波M2、S2、N2和K2，4個周日潮波K1、O1、P1、Q1以及3個長周期潮波Mf、Mm、Saa)，Ak,j和φk,j分別為潮波分量j在k方向上的振幅和格林尼治相位，ωj和χj分別為潮波分量j的角頻率和天文幅角初相，fj和μj分別為振幅和相位的節點調制改正。本文主要考慮8個周日潮波和半日潮波，將式(1)線性化后得到：

Ask.jsin(ωjt+χj)]

(2)

其中，

Ack,j=fjAk,jcos(φk,j-μj)

Ask,j=fjAk,jsin(φk,j-μj)

式中，Ack,j和Ask,j分別為8個潮波3個方向上的正弦系數及余弦系數。將48個潮波參數均當作未知數，與測站坐標等參數一并求解。

2.2 數據處理策略

使用GIPSY/OASIS-Ⅱ軟件(版本6.4)進行靜態PPP解算[4]。為與JPL精密衛星軌道、精密鐘差產品的框架保持一致，采用FES2004全球海潮模型[5]計算各測站點在整體地球(包括固體地球、海洋及大氣等)質心為原點框架下的海潮負荷位移和相位，作為海潮負荷位移參數估計先驗值加入到原始GPS數據處理中。GIPSY解算過程中部分參數設置見表1。

表1 PPP靜態解算參數設置

使用GIPSY解算策略求解出8個潮波單天的振幅及相位，頻率相近的2個潮波之間的相關性最高可達0.8，因此難以從單天解算結果中獲取準確的振幅及相位。本文采用Yuan等[6]的方法，利用卡爾曼濾波對單天潮波參數進行融合。圖2為DUNT站的潮波參數隨融合天數增加而收斂情況，當融合天數超過1 000 d時，8個潮波振幅穩定收斂，本文189個GPS測站解算天數均超過1 000 d。

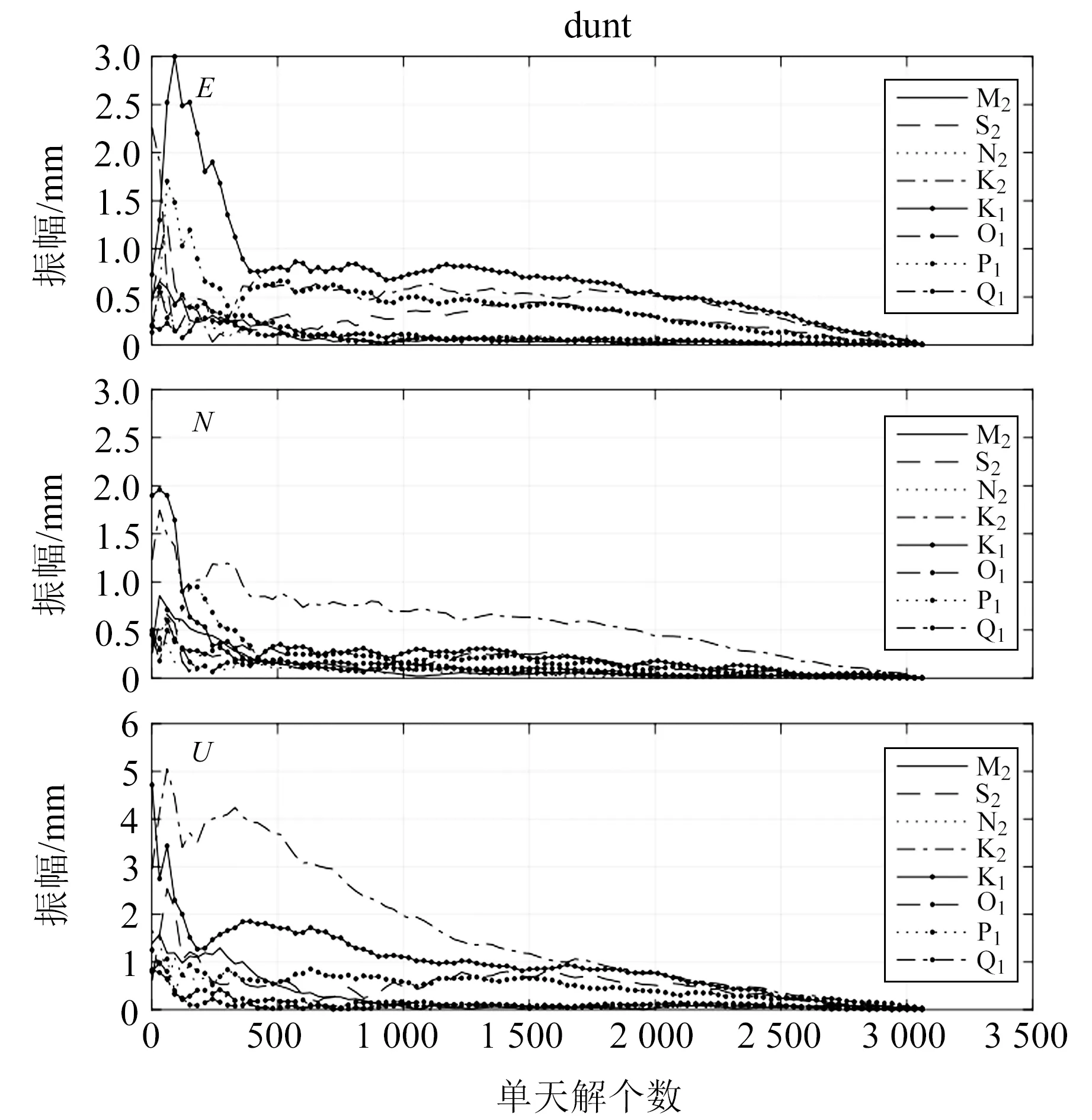
圖2 DUNT站潮波參數收斂性Fig.2 Tidal estimation convergence at DUNT station

海水質量、大氣、陸地水及冰川等的影響會導致地球整體質量中心(CM)相對于固體地球質量中心(CE)產生周期性運動，因此在海潮負荷研究中有必要進行地心運動改正。本文根據Yuan等[6]計算的8個潮波的地心運動改正參數，將所有GPS解算結果及模型計算結果統一至CE框架下。

3 結果分析

3.1 不同海潮模型差異分析

為驗證全球海潮模型在研究區域內的誤差分布情況，以M2潮波為例，選取16個驗潮站2012～2019年的實測數據，根據調和分析原理提取出M2潮波的潮高，并與全球海潮模型值進行比較(所有模型均采用雙線性插值至0.125°格網)，部分結果見表2(單位m)。此外，基于PREM地球模型確定格林函數和7種全球海潮模型[7]，利用SPOTL軟件計算研究區域內M2潮波垂直方向的負荷位移(空間分辨率為0.1°)，以此來分析不同全球海潮模型計算的負荷位移改正的差異性。圖3為選定區域中7種全球海潮模型確定的M2潮波負荷位移改正值的標準差，圖中黑色五角星為表2中的驗潮站，黑色三角形為其他驗潮站的分布情況。

北島北部奧克蘭地區7種海潮模型確定的M2潮波負荷位移改正的標準差最大可達1.1 mm，南、北島之間塔斯曼灣M2潮波負荷位移改正標準差可達1.5 mm。在驗潮站AUCT，不同海潮模型之間潮高差異較大，且與驗潮站實測數據相差也較大，這說明在奧克蘭地區海潮負荷位移標準差較大，因此在海岸復雜地區全球海潮模型尚待進一步精化。除奧克蘭和塔斯曼灣地區，其他地區(如驗潮站OTAT附近)不同模型RMS低于0.3 mm，且海潮模型值與驗潮站潮高實測結果吻合較好，說明海潮模型在這些地區建模精度較高。

表2 M2潮波潮高統計

圖3 M2潮波負荷位移垂直分量標準差及驗潮站分布Fig.3 Standard deviation of the vertical M2 OTL displacement and the locations of the tide gauges

3.2 海潮模型改正值與GPS測定參數比較

為評定不同海潮模型在新西蘭地區的建模精度，利用SPOTL軟件，選取PREM地球模型推導的格林函數(LGF)和7種全球海潮模型計算CE框架下各GPS站點處的潮波參數，并求取GPS測定的位移參數與海潮模型改正值之間的均方根誤差(RMS)[6]。對于8個主要潮波分量j、坐標分量k，所有測站(N=189)的GPS測定的位移參數值與模型改正值之間的RMS計算公式為：

(3)

其中，

Zj,k,n=AGPS(cosφGPS+isinφGPS)j,k,n-

Amodel(cosφmodel+isinφmodel)j,k,n

(4)

式中，A為振幅，φ為格林尼治相位。

圖4給出了GPS測定參數與7種全球海潮模型改正值的RMS。可以看出，水平方向上，所有潮波參數RMS均小于1 mm，N2、Q1潮波GPS測定的位移參數值與模型值RMS僅0.1 mm，不同海潮模型之間的RMS無顯著區別；垂直方向上，S2、K2和K1潮波的RMS顯著大于其他潮波，由于K2潮波周期與衛星星座周期一致，GPS軌道周期與K1潮波周期相近，因此衛星軌道誤差和多路徑效應可能分別是導致K1和K2潮波GPS測定的海潮負荷位移參數與模型改正值差異較大的直接原因[6]。

FES2004海潮模型在M2、S2潮波垂直方向上RMS值最大，原因可能是其吸收的測高衛星數據在復雜海岸線精度較低且未考慮地心運動改正[5]。同時由表2可知，其M2潮高模型值與驗潮站實測結果差異最大。對于M2潮波，驗潮站實測潮高與GPS實測位移參數均顯示，FES2004和EOT11a海潮模型不適用于新西蘭地區。TPXO7.2海潮模型在新西蘭地區精度最高，其中4個月球相關潮波(M2、N2、O1和Q1)與GPS測定海潮負荷位移參數的RMS值在水平方向小于0.5 mm，垂直方向小于0.7 mm。

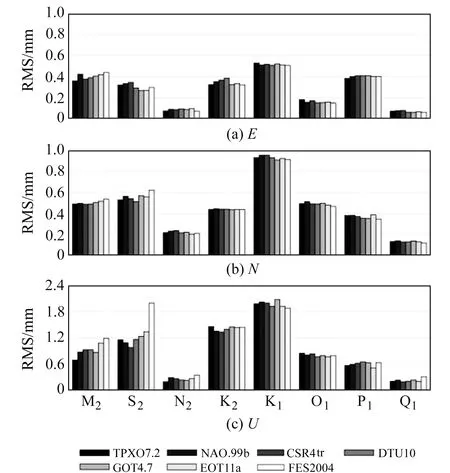
圖4 GPS海潮負荷位移估值與不同海潮模型預測之間的RMSFig.4 RMS of the GPS OTL displacement estimates against predictions derived by different ocean-tide models

3.3 不同地球模型對海潮負荷位移的影響

為研究不同地球模型對海潮負荷位移建模的影響，使用4種具有球對稱、非自轉、完全彈性和各向同性(SNREI)性質的地球模型(PREM地球模型、AK135地球模型、Gutenberg-Bullen地球模型和1066A地球模型)計算的LGF與TPXO7.2海潮模型進行離散褶積積分，利用SPOTL軟件計算189個GPS測站點處的海潮負荷位移參數[8]，并利用式(3)計算RMS。

圖5顯示，除M2、N2潮波外，其余6種潮波對于不同LGF與TPXO7.2海潮模型組合的計算結果差異不大，地球模型對此6種潮波負荷位移影響并不敏感，目前難以利用GPS實測值進行有效區分。M2、N2潮波RMS值分布的相似性可能是由于M2潮波與N2潮波的負荷位移特征相似且振幅呈一定比例所致。Yuan等[6]指出，不同地球模型在M2潮波三維方向上RMS值大小順序不一致，可能是由于固體潮模型誤差所致。

圖5 GPS海潮負荷位移估值與不同地球模型預測值之間的RMSFig.5 RMS of the GPS OTL displacement estimates against predictions derived by different earth models

4 GPS測定的位移參數估值與模型值殘差分析

不同海潮模型和地球模型均在M2潮波差異最為明顯。以M2潮波為例，選取TPXO7.2全球海潮模型和PREM地球模型獲取GPS測站處海潮負荷位移改正值，并與GPS測定的位移參數求取矢量差，結果見圖6。由圖可見，水平方向殘差呈現出明顯的區域一致性。Yuan等[6]指出，依據IERS2010使用的固體潮模型不確定性在1 mm左右，與本文殘差大小基本一致。垂直方向上，沿海地區的部分站點殘差顯著大于內陸地區測站殘差。Bos等[9]指出，采用不同的數值計算方法、海水密度和海岸線格網精化方法對海潮負荷位移的影響在0.5 mm左右，因此海潮模型誤差仍是沿海地區殘差的主要組成部分。

北島奧克蘭地區和南島達尼丁地區(驗潮站OTAT附近，圖3)垂直方向上的殘差分別達到1.8 mm和1.4 mm，7種海潮模型標準差在奧克蘭和達尼丁區域分別約為1.0 mm和0.2 mm(圖3)，本文解算的M2潮波垂直方向GPS中誤差小于0.3 mm，因此推測，前者殘差主要來源于海潮模型誤差。而海潮模型誤差及GPS測定的位移參數誤差之和不足以完全解釋驗潮站OTAT周圍GPS站點處的海潮負荷位移殘差，因此該殘差可能反映出當前使用的地球模型還存在缺陷[9]。本文所采用的PREM地球模型是SNREI地球模型，其未考慮真實地球結構的地幔滯彈性和散耗效應等特征，因此由PREM地球模型推導的負荷格林函數很大程度上將導致海潮負荷位移計算出現偏差[9]。

圖6 M2潮波的海潮負荷位移殘差在東、北和垂直方向上的矢量分布Fig.6 Spatial distribution of phasor vector of OTL residuals for the M2 constituent at E, N, and U component

5 結 語

本文采用新西蘭地區189個連續運行觀測站11 a的觀測數據，基于GPS靜態PPP方法精確測定了新西蘭地區的海潮負荷位移，將GPS測定潮波參數與模型進行比較后得到以下結論：

1)驗潮站實測值與GPS潮波位移參數實測值均反映出TPXO7.2模型在新西蘭地區建模精度最高，半日潮波的GPS測定結果與海潮模型值之間的RMS在三維方向上小于1 mm。

2)不同地球模型之間的差異主要體現在M2、N2潮波，其余6種潮波負荷位移對不同地球模型的選取不敏感。

3)海潮模型在部分復雜海岸區域負荷位移誤差較大。部分站點異常的殘差值可能反映出本文采用的SNREI地球模型存在缺陷。

本文GPS靜態解算結果可用于新西蘭沿海區域海潮負荷位移改正以及對地球模型的參數進行約束，如考慮軟流圈彈性散耗效應等。