聯合優化方向圖合成與頻譜兼容的MIMO雷達波形設計

陳寧康，魏 平，高 林，張花國

(電子科技大學信息與通信工程學院 成都 611731)

發射單一波形的相控陣雷達在目標檢測、抗復雜干擾、目標參數估計等方面的性能難以滿足復雜的實際需求，MIMO 雷達因其具有波形分集的自由度優勢，能夠實現上述方面的更優性能。MIMO 雷達發射方向圖合成是通過設計發射波形的模值和相位，將發射能量聚焦在感興趣的空間方向上，減少發射能量在其他方向上的分布；而隨著無線通信設備(尤其是智能移動設備)的指數級增長，電磁環境中的頻譜資源日益擁堵，對雷達與無線通信設備的同頻相互干擾的抑制能力，亦即頻譜共存能力也成為設計發射波形時必須考慮的重點。

基于MIMO 雷達發射方向圖擬合的波形設計方法主要分為兩步法和一步法兩類。

兩步法即先設計發射波形的協方差陣，再在此基礎上設計波形矩陣。文獻[1]提出使用半定二次規劃算法設計發射波形協方差陣來擬合方向圖模板，能達到最優性能，但計算量很大。文獻[2]提出循環算法擬合方向圖模板，先設計發射波形協方差陣，再設計發射波形矩陣。文獻[3]提出的算法在恒模約束和相似性約束下設計發射波形，在兼具參考波形性能的前提下具有較好的方向圖擬合效果。

一步法即直接通過方向圖模板匹配設計發射波形矩陣。文獻[4]利用傅里葉級數分解方向圖模板，進而使用無約束優化設計發射波形。文獻[5]利用交替乘子算法設計恒模發射波形匹配任意形狀方向圖，達到了接近最優的性能，但針對大快拍數的發射波形需求，其計算量較大。文獻[6]將設計波形擬合方向圖的代價函數建模為 lp范數模型，再基于MM(majorization-minimization)算法迭代優化匹配系數與波形，得到低旁瓣、平坦的合成波束圖。

雷達系統頻譜兼容波形設計問題一般分為兩類：一類為避開無線通信系統頻段的雷達波形設計，此時通信系統受干擾減少，傳輸速率和誤碼率都能得到提升，雷達系統的探測能力也會更少受到同頻段通信信號干擾；另一類為雷達與無線通信系統頻段共用。

文獻[7]在多目標存在下，通過最小化空－頻域凹陷區的波形積累能量，完成發射波形與接收濾波器聯合設計，達到頻譜共存的性能，計算量優于半正定松弛方法，但仍隨著陣元數、采樣數升高而急劇增高。文獻[8]設計了模板擬合方法同時滿足頻譜兼容、旁瓣電平的需求，主要思路仍然是每步迭代中使用頻譜模板的加載。文獻[9]提出一種拉格朗日規劃神經網絡的方法，較好地解決加權最小二乘擬合頻譜模板的問題，但收斂速率慢，計算量較大。文獻[10]提出基于MM 算法的頻譜擬合迭代優化算法，引入頻譜阻帶的懲罰權向量以及設計加速收斂方法，能高效靈活地擬合頻譜模板。文獻[11]概述了MM 算法框架，介紹了其基本原理和擴展算法，以及在信號處理、通信和機器學習應用中問題的解決方案。

總結相關文獻，只有極少數文獻在設計發射波形時將波束圖合成與頻譜塑形聯系起來[12]，但該方法使用矩陣求逆，運算量大。這種聯合優化的工程應用價值大，既能將輻射能量投送到指定空域，又避免干擾到鄰近頻段的通信系統，以及降低鄰近頻段阻塞式干擾的影響。否則在執行雷達探測任務時，處在沖突頻段的通信系統的誤碼率性能會受顯著影響，處在沖突頻段的阻塞式干擾也容易使雷達探測性能惡化。

本文針對聯合優化雷達發射波形的方向圖合成性能與頻譜兼容能力，提出基于MM 框架的迭代優化算法。首先利用空域和頻域先驗信息，建模波束圖合成與頻譜塑形聯合優化的問題；迭代中，在已知上一步迭代的波形的情況下，更新當前步的匹配系數；再對均方誤差代價函數進行放縮，構造替代函數；進而最小化替代函數，得到當前步迭代的最優發射波形。該算法能用較小的計算量得到接近理想的擬合效果。

1 優化問題模型

1.1 方向圖合成問題模型

集中式MIMO 雷達的M 個陣元以間距為d 的均勻線陣形式排列，發射場景如圖1 所示。

圖1 集中式MIMO 雷達發射波形能量聚焦場景

雷達的發射波形矩陣為S=[s1,s2,···,sN]，波形快拍數為N，第n 時刻的陣列空域波形向量為sn=[s1(n),s2(n),···,sM(n)]T。遠場目標位于空間角度θ上，陣列發射導向矢量為：

陣列發射波形在空間角度θ處合成的平均功率，亦即方向圖為：

設空間角度格點數為G，方向圖模板為pd=[pd(1),pd(2),···,pd(G)]T，空間匹配系數為 α，則方向圖合成的問題是找到波形滿足代價函數最小的優化問題，其代價函數可建模為所形成方向圖與方向圖模板之間的均方距離：

恒定模數約束可防止功率放大器的非線性失真，從而使發射器的效率最大化。具體而言，將波形矩陣的標準化包絡寫為：

1.2 頻譜塑形問題模型

陣列各陣元發射時域信號，即波形矩陣S 的各行的頻譜為FH(S(m,:))T，S(m,:)為波形矩陣的第m 行，傅里葉變換矩陣表示為：

1.3 方向圖合成與頻譜塑形聯合優化問題

設 γ為調整兩種代價函數的權重系數，聯合代價函數是式(3)與式(5)的加權和：

聯合優化的問題可以表示為：

問題表明需要聯合考慮發射波形所形成方向圖與方向圖模板均方距離，以及各陣元發射波形在頻域上與理想頻譜模板均方距離同時達到最小。

2 波形設計算法

2.1 算法推導

2.1.1 匹配系數更新

代價函數在第k 次迭代結果為：

2.1.2 替代函數的替代優化

將式(13)、式(14)代入代價函數(9)后得到J (S,α(k+1), μ(k+1))，忽略常數項，對它進行最小化的問題可寫成：

忽略常數項，替代函數尋優的問題寫成：

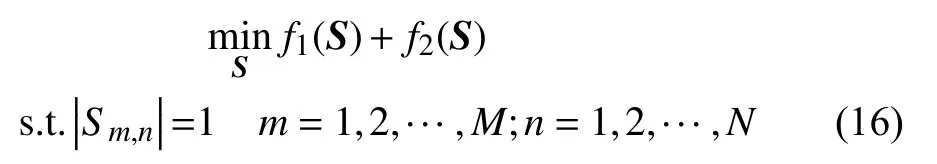
其中，

由矩陣跡的性質，可得：

由二階泰勒展開，式(14)中目標函數的二次項可放縮為替代函數：

Hessian 矩陣被對角矩陣替代，其系數為：

忽略常數項，f1(S)替代函數優化問題為：

一次項為：

f1(S)+f2(S)的替代函數優化問題為：

式(25)中替代優化問題寫成矩陣問題：

上述優化問題被重構為：

其中，

考慮到恒模約束，波形矩陣更新為S=ej∠Ω(k)。

2.2 計算復雜度分析

3 仿真結果

本節對提出的波形設計算法進行數值算例的仿真。分別在不同場景需求下，模擬算法的方向圖擬合性能與頻譜擬合性能。方向圖擬合的SQP 算法源自文獻[1]。參數設置：10 陣元均勻線陣、快拍數32，方向圖擬合誤差占總誤差比重γ=0.5。單主瓣平頂方向圖主瓣為[-30?,30?]，多主瓣平頂方向圖主瓣為[-50?,-30?]∪[-10?,10?]∪[30?,50?]。第一個頻譜模板的阻帶歸一化頻率范圍為[0.2,0.5]，深度為-20 dB；第二個頻譜模板的阻帶歸一化頻率范圍為[0, 0.061 7] ∪ [0.098 8, 0.246 9] ∪ [0.259 3,0.284 0] ∪ [0.308 6, 0.382 7] ∪ [0.407 4, 0.493 8] ∪[0.518 5, 0.555 6] ∪ [0.938 3, 1]，深度為-20 dB。

3.1 單主瓣平頂方向圖與寬阻帶頻譜聯合擬合

單主瓣平頂方向圖應用場景：空間能量聚焦目標區域為DOA 相對集中的慢變空間范圍。

擬合方向圖的曲線如圖2 所示，本文算法設計的波形合成的方向圖與SQP 算法合成的方向圖貼近，且本文算法不需要求逆運算，計算量較小，對于頻率捷變MIMO 雷達這類需要不斷重新計算的應用具有優勢。

頻譜擬合的曲線如圖3 所示，藍色虛線為頻譜模板，其他顏色為各陣元發射波形的頻譜。各陣元發射波形的頻譜在通帶貼近模板，且波紋較小；阻帶電平最淺處達到-13 dB，最深處超過-30 dB，能夠有效地避免對鄰近無線通信頻段形成干擾。

圖2 單主瓣平頂方向圖擬合結果

圖3 寬阻帶頻譜擬合結果

3.2 多主瓣平頂方向圖與多零陷窄阻帶頻譜聯合擬合

多主瓣平頂方向圖應用場景：空間能量聚焦目標區域為DOA 相對分散的多個空間范圍。

擬合方向圖的曲線如圖4 所示，本文算法設計的波形合成的方向圖與SQP 算法合成的方向圖貼近，旁瓣電平更低，且不需要求逆運算，計算量較小，對于頻率捷變MIMO 雷達這類需要不斷重新計算的應用具有優勢。

頻譜擬合的曲線如圖5 所示，藍色虛線為頻譜模板，各陣元發射波形的頻譜在通帶貼近模板，且幾乎沒有波紋；阻帶電平最淺處達到-10 dB，最深處超過-30 dB。靈活多變的頻譜模板設置，使得雷達能夠有效地避免對處于模板阻帶頻段的無線通信系統形成干擾，也能降低處于模板阻帶頻段的阻塞式干擾對雷達探測性能的影響。

圖4 多主瓣平頂方向圖擬合結果

圖5 多零陷窄阻帶頻譜擬合結果

4 結 束 語

本文提出的算法設計MIMO 雷達發射波形，聯合優化方向圖合成性能和頻譜塑形性能。聯合優化問題被建模為加權均方誤差代價函數，優化問題是非凸非平滑的。首先對優化問題的模型進行建模，再對均方誤差代價函數進行放縮，構造替代函數；進而優化替代函數，得到較小代價函數值對應的波形。本文提出的迭代優化算法，具有接近理想的方向圖擬合性能與頻譜擬合性能，且運算量小。多個應用場景下的仿真和數值結果證明了所提方法的有效性。

未來的工作會著重關注雷達波形的探測性能，例如自相關性能、多普勒性能等，將這些性能與方向圖擬合、頻譜擬合聯合考慮。