基于Hadamard 矩陣構造部分重復碼

王 靜，孫 偉*，何亞錦，沈克勤，張鑫楠，劉向陽

(1. 長安大學信息工程學院 西安 710064；2. 國防科技大學信息通信學院 西安 710106)

近年來，由于數據量的快速上升，急需一種適宜的大數據存儲系統。分布式存儲系統由許多廉價磁盤組成，以其突出優勢成為海量數據存儲的有效系統，并被廣泛部署和使用[1]。但在分布式存儲系統中，節點容易發生故障，造成數據丟失。因此，故障節點的快速修復研究成為了分布式存儲系統可靠性的重中之重。

目前，分布式存儲系統主要通過復制和糾刪碼策略來恢復節點故障。復制策略中三副本復制最為常見，故障節點修復具有較低的修復帶寬開銷，但需要存儲大量的副本數據，存儲開銷較大。糾刪碼策略通過增加校驗數據塊來確保數據存儲的可靠性，實現故障節點修復，且存儲開銷較小。雖然糾刪碼彌補了復制策略存儲開銷大的缺點，但是糾刪碼在修復故障節點時的修復帶寬開銷過大[2]。

鑒于復制和糾刪碼策略存在上述局限性，文獻[3]將網絡編碼應用到分布式存儲中，提出了再生碼的概念，降低了故障節點的修復帶寬開銷。現在再生碼研究重點在最小存儲再生(minimum storage regeneration, MSR)碼和最小帶寬再生(minimum bandwidth regeneration, MBR)碼[4-5]。再生碼在修復故障節點時，需要連接大量存活節點以獲得較低的修復帶寬開銷，且在修復過程中涉及有限域運算，計算復雜度相對較高。隨后，文獻[6]提出了局部修復碼(locally repairable codes, LRC)，使修復過程中需要連接的存活節點數較小，修復帶寬開銷較低，具有較好的修復局部性。將再生碼和局部修復碼結合，文獻[7-8]提出了局部再生碼的概念，達到存儲-帶寬開銷的最佳折中。其中，基于系統MSR碼的局部再生碼，故障局部碼可以通過相鄰局部碼進行協作修復[9]。

文獻[10]提出了一種精確最小帶寬再生碼—部分重復(fractional repetition, FR)碼，故障節點修復過程中的計算復雜度和修復帶寬開銷都有所降低，可以實現故障節點的精確無編碼修復。近年來，許多研究人員對FR 碼進行了研究，文獻[11]利用組合設計來構造FR 碼。隨后，學者們又相繼給出了幾種基于組合結構的FR 碼構造，包括基于射影幾何的FR 碼構造[12]、基于正則圖的FR 碼構造[13]及基于可分組設計的FR 碼構造[14]。

現有FR 碼對于故障節點的修復，特別是多節點故障修復，其修復帶寬開銷和修復局部性較高，同時修復復雜度也較高。文獻[13]提出了基于正則圖構造FR 碼，隨后文獻[15]提出了運用網格構造FR 碼，但其都只能修復單節點故障。基于相對差集的FR 碼構造，能夠修復分布式存儲系統中的多節點故障，但是隨著參數的增大，其節點存儲容量和構造復雜度會隨之增大[16]。而且常見的FR 碼構造隨著系統規模和參數的增大，其節點數或節點容量增大，構造復雜度也會增大。本文提出基于Hadamard 矩陣構造FR 碼，同時對其進行分組，運用8 階Hadamard 矩陣提出了分組構造FR(Hadamard grouping fractional repetition, HGFR)碼的一般算法，實現故障節點的局部修復。基于Hadamard 矩陣分組構造FR 碼可以對多個節點故障進行快速精確無編碼修復，有效降低了運算復雜度，同時運用了分組可以實現組內修復，復雜度進一步降低，實現故障節點的快速修復。理論分析發現，與RS 碼和SRC 簡單再生碼相比，設計的FR 碼在分布式存儲系統節點發生故障時，修復局部性、修復復雜度和修復帶寬開銷進一步降低，且修復效率提高，減少了故障節點的修復時間。

1 Hadamard 矩陣和部分重復碼

1.1 Hadamard 矩陣

Hadamard 矩陣是在工程技術上運用較多的一類矩陣，Hadamard 矩陣是特殊的1、-1 二元矩陣，具體定義如下：

定義1[17-18]n階方陣 Hn，其元素為1 或-1，并且滿足：

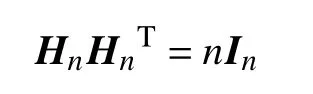
稱 Hn為n階Hadamard 矩陣，其中 In是n階單位矩陣。

若Hn的第1 行和第1 列全是1，該Hn為Hadamard矩陣的標準型。以下所涉及的Hadamard 矩陣 Hn均為Hadamard 標準型矩陣。

Hadamard 矩陣有如下一些性質：

1) 將Hadamard 矩陣的任意兩行(或兩列)交換，Hadamard 矩陣的任意一行(或一列)的所有元素乘以-1，得到的矩陣仍然為Hadamard 矩陣。

2) 若 Hn是 n階Hadamard 矩陣(n ＞2)，則 n是 4 的倍數。

定義2[19]令：

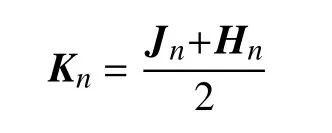
其中 Jn表示元素全為1 的n階矩陣，則得到n階0-1矩陣 Kn。

性質1 矩陣 Kn中除第一行之外，每一行都有n/2個1 和 n/2個0。

1.2 FR 碼

FR 碼是在MBR 碼基礎上提出的，典型的FR碼由兩部分組成，外部的MDS 碼和內部的重復碼[20]。

定義3(FR 碼)[21]分布式存儲系統中參數為(n,k,d)的部分重復碼C=(η,M)，將數據塊復制ρ倍(即重復度為 ρ)，特定地， n個子集的集合M={M1,M2,···,Mn}，子集中的元素都來自于集合η={1,2,···,θ}。

同時應滿足以下兩個條件：

1)每個子集的大小均為d ；

2) η中的每個元素屬于 M中的ρ個子集。

上述定義中，數據塊是經過MDS 編碼后的數據塊。FR 碼的實質是將數據塊復制ρ倍，然后將其排列到n個節點，同時使相同的數據塊不出現在同一個節點上。圖1 為經過(12,9)MDS 編碼后構成(12,9,4)FR 碼，其中ρ為2，數據復制2 倍，每個節點存放4 個編碼數據塊。

FR 碼修復故障節點時直接從未失效節點中下載丟失的所需數據塊，不進行編譯碼操作即可完成故障節點的迅速修復。FR 碼可實現精確無編碼修復，修復帶寬開銷和修復時間較低，修復復雜度較小，同時能夠容忍ρ-1個節點故障。

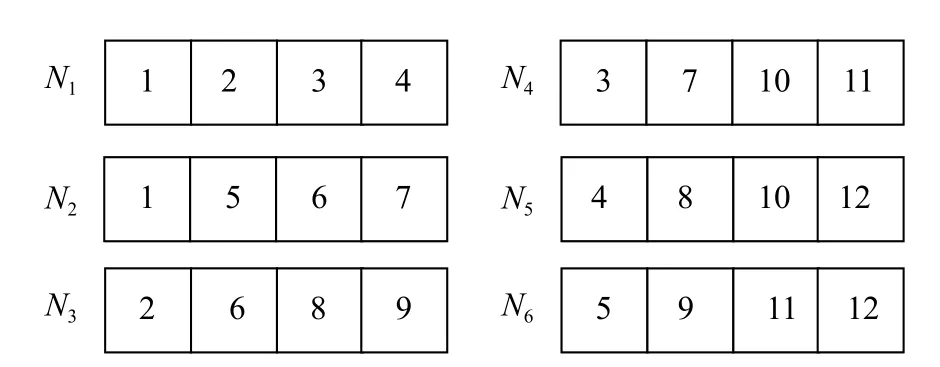
圖1 (12,9,4)FR 碼

2 基于Hadamard 矩陣構造FR 碼

本節基于Hadamard 矩陣構造FR 碼。首先選取一個4t(t=1,2,3,···)階的Hadamard 矩陣，對其進行簡單的變換得到所需要的矩陣；再將矩陣與分布式存儲節點和編碼數據塊相對應，矩陣的行代表存儲節點，矩陣中不同的列表示不同的編碼數據塊。由Hadamard 矩陣引出FR 碼一般性構造算法，其具體步驟如下：

1) 將原始文件 M分成k個原始數據塊，這里k ≥2。對該 k個原始數據塊采用(n,k)MDS 編碼(n ≥k)，得到n個編碼數據塊c1,···,ck-1,ck,ck+1,···,cn，n個編碼數據塊包括k個原始數據塊和n-k個校驗數據塊；

2) 取一個n+1 階標準型Hadamard 矩陣Hn+1，其中n+1=1,2，或n+1=0(mod4)；

3) 根據公式：

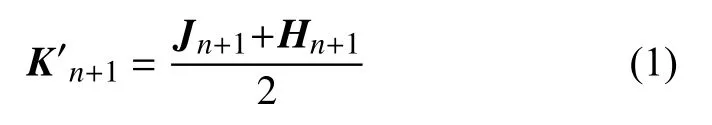
得到0-1 矩陣K′n+1(n ≥k)，其中Jn+1表示元素全為1 的n+1階矩陣，Hn+1為標準Hadamard 矩陣，需滿足n+1為4 的倍數；

4) 對0-1 矩陣K′n+1進行變換，將第一行第一列刪去得到新矩陣 Kn；

5) 通過矩陣 Kn構造FR 碼，具體過程為：

① 矩陣 Kn中每一行代表一個節點，用矩陣Kn中的第i行表示分布式存儲系統中的第i個存儲節點 Ni，共有n個存儲節點，i=1,2,···,n；

② 由以下公式構造FR 碼：

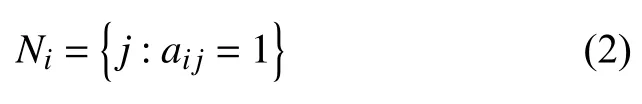
式中，j=1,2,···,n； i表示第i個FR 節點； aij表示矩陣第i 行第j 列的值； Ni表示FR 碼的存儲節點。 Ni中包含的數據塊為矩陣 Kn中第i行所有1 所對應的列數，將列數提取出即得到一個節點所存儲的數據塊，構成了所需FR 碼。

采用上述FR 碼的一般性構造算法，在包含n=11個存儲節點的分布式存儲系統中，構造FR 碼。選取如式(3)所示的12 階Hadamard 矩陣，利用式(1)對該Hadamard 矩陣進行變換，進一步得到所需的11 階矩陣 K11，如式(4)所示。采用該 K11矩陣，按照步驟5)構造得到FR 碼，該FR 碼的節點存儲結構具體如圖2 所示。其中矩陣的行代表分布式存儲系統中的存儲節點，矩陣中不同的列表示不同的編碼數據塊，每個存儲節點存儲d=5個編碼塊，編碼塊的重復度ρ=5。

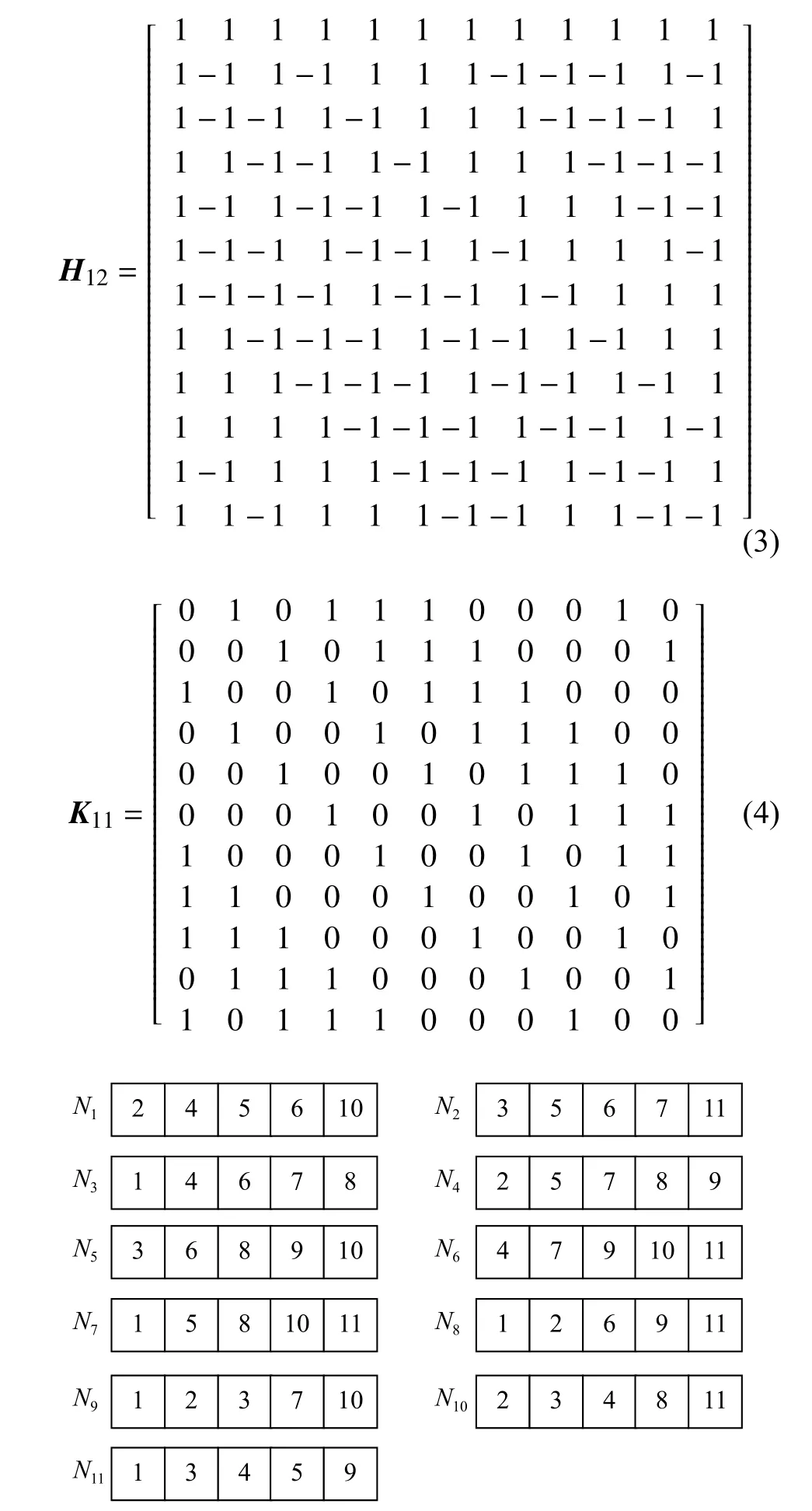
圖2 FR 碼的節點存儲結構圖

當一個節點發生故障時，可以運用其他節點對故障節點進行修復，在其他節點中找到并下載含有故障節點的數據塊，故障節點即完成了修復，且該過程不需要進行編碼譯碼操作。對于圖2 中的FR碼，若節點 N1發生故障，可以分別從存活節點 N3中下載數據塊4 和6，從存活節點 N4中下載數據塊2 和5，以及存活節點 N5中下載數據塊10，實現節點 N1的修復。對于兩個節點發生故障的情況，與一個節點故障修復的方法相同。

3 基于Hadamard 矩陣構造分組FR 碼

運用Hadamard 矩陣構造FR 碼發現，隨著Hadamard 矩陣階數的增加，FR 碼的重復度和節點存儲容量也會隨之增加，從而導致存儲開銷也相應地增加，故障節點修復性能受到一定限制。為此，本節引入分組構造的思想構造部分重復碼。當Hadamard 矩陣的階數為12 時構造的FR 碼的重復度為5，重復度較大；當階數為8 時FR 碼的重復度降為3，更滿足實際存儲需求，所以本文利用8 階標準Hadamard 矩陣構造分組FR 碼。

3.1 基于Hadamard 矩陣構造分組部分重復碼

對分布式存儲系統節點進行分組，并利用8 階Hadamard 矩陣構造分組FR 碼(hadamard grouping fractional repetition, HGFR)。分組FR 碼的具體構造算法如下：

1) 取一個8 階標準Hadamard 矩陣 H8；由上節構造部分重復碼方法的步驟1)～步驟4)得到新矩陣 K7，并利用新矩陣 K7構造FR 碼；

2) 記原始文件M 包含s個原始數據塊，將原始數據塊進行分組，得到t個局部修復組，每組分配k=5個原始數據塊。包含以下幾種情況：

① 如果s可以被k=5整除，即s=tk ，此時每個局部修復組內首先進行(7, 5)MDS 碼編碼，然后采用步驟3)中的矩陣 K7構造FR 碼；

② 如果s不能被k=5整除，即s=tk+m且m=1，前t-1 個局部修復組采用(7, 5)MDS 碼以及矩陣K7構造FR 碼，第t 個局部修復組采用(7,6)MDS碼以及矩陣 K7構造FR 碼；

③ 若s=tk+m且m=2，前t-2個局部修復組采用(7, 5)MDS 碼以及矩陣 K7構造FR 碼，第t-1 個和第t 個局部修復組采用(7, 6)MDS 碼以及矩陣K7構造FR 碼；

④ 若s=tk+m且m=3或者4 時，前t-1 個局部修復組采用(7,5)MDS 碼以及矩陣 K7構造FR 碼，第t 個局部修復組采用(7,m)MDS 碼以及矩陣 K7構造FR 碼。

以包含s=11個數據塊的原始文件為例，s=2k+1，這里m=1，滿足情況②。第1 個局部修復組采用(7,5)MDS 碼以及矩陣 K7構造FR 碼，第

2 個局部修復組采用(7,6)MDS 碼以及矩陣 K7構造FR 碼。構造的分組FR 碼如圖3 所示。

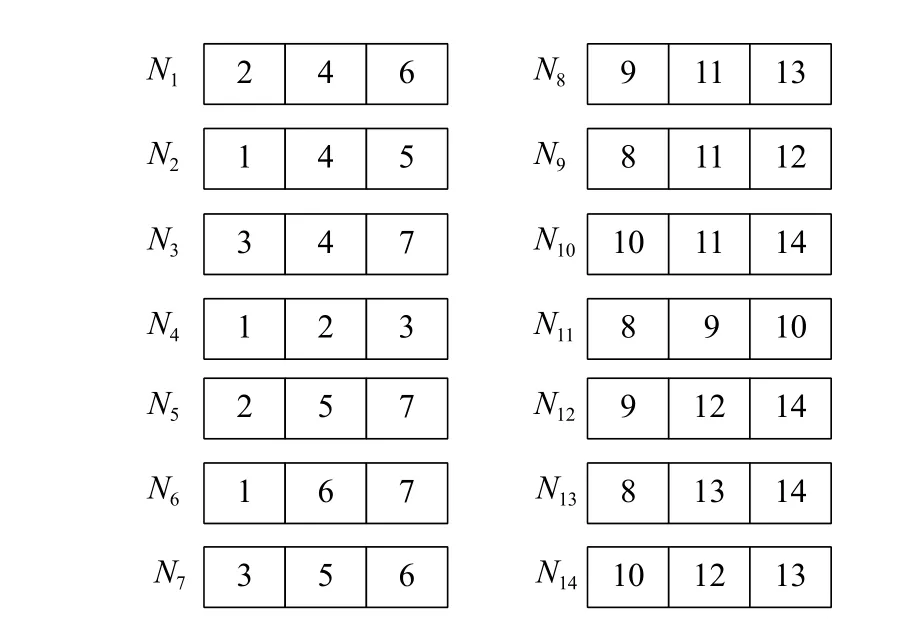
圖3 分組FR 碼的節點存儲結構圖

3.2 故障節點修復

下面考慮分布式存儲系統采用基于Hadamard矩陣的分組FR 碼，其故障節點的修復。考慮到3 個以上節點同時故障的概率很低，本文只考慮分布式存儲系統中1 個、2 個或者3 個節點故障，且在同一個或者不同局部修復組內的情況。具體故障節點修復過程如下：

1)當分布式存儲系統只有1 個節點故障，此時只需考慮在一個局部修復組內對單一故障節點進行修復。具體地，在該局部修復組內其他存活節點中找到含有故障節點的數據塊，直接下載故障節點丟失的數據塊，即可完成故障節點修復，該過程不需要進行編碼操作。如圖2 所示，如第一個局部修復組中第一個節點發生故障，可以下載節點 N2、 N4、N6中的2、4 和6 這3 個數據塊完成第一個節點的修復。

2)當分布式存儲系統中有2 個節點同時發生故障時，存在以下兩種情況：① 2 個故障節點在同一局部修復組內，可以從剩余的5 個存活節點中下載故障節點所含有的數據塊，完成故障節點的快速修復；② 發生故障的2 個節點不在同一局部修復組，則需要在兩個修復組內分別對其組內的故障節點進行修復。在圖2 中，如節點 N2和節點 N10發生故障導致數據塊丟失，可以在第一個局部修復組內從節點 N1、 N4、 N5中分別下載數據塊4、1 和5 完成節點 N2的修復，在第二個局部修復組內從節點N9、 N11、 N13下載數據塊11、10 和14 完成節點N10的快速修復。

3)當分布式存儲系統中有3 個節點同時發生故障，存在以下兩種情況：①發生故障的3 個節點不在同一局部修復組，該情況下的故障節點修復與前面兩種修復過程完全一樣，只需直接從局部修復組中下載所需的數據塊；②發生故障的3 個節點在同一局部修復組中，如果3 個故障節點中沒有同時含有同一個數據塊，則可以直接從其他存活節點中下載丟失的數據塊，完成故障節點的修復；否則，需要運用MDS 編碼進行修復。如圖2 中節點 N1、N2、 N3發生故障，剩余存活節點無法直接修復，需要從存活節點下載數據塊進行MDS 編碼修復數據塊4，即完成故障節點 N1、 N2、 N3的精確修復。

4 性能分析

本節對提出的基于Hadamard 矩陣構造分組FR 碼進行性能分析，修復帶寬開銷、修復局部性、修復復雜度為分析的主要性能，并與SRC 簡單再生碼以及RS 碼進行比較。取文件大小M=1 000 Mb，SRC 簡單再生碼的子文件數f =4。

4.1 修復帶寬開銷

當節點發生故障時，修復故障節點被下載的數據量大小稱為修復帶寬開銷。在分布式存儲系統中，原文件大小為 M，當發生單節點故障時，若采用(n,k)RS 碼，則需要下載全部的原文件來修復故障節點，所以采用(n,k)RS 碼修復單節點故障的修復帶寬開銷為文件大小 M；對于(n,k,f)SRC 簡單再生碼，每個節點存儲f+1個數據塊，每個數據塊大小為M/fk，當一個數據塊發生故障， f個數據塊被下載進行修復，所以1 個節點發生故障的修復帶寬開銷為(f+1)M/k；如果采用基于Hadamard 矩陣的分組FR 碼，每個數據塊大小為M/k，每個節點含有3 個數據塊，所以基于Hadamard 矩陣的分組FR 碼的單節點故障的修復帶寬開銷為3M/k。單節點故障的3 種編碼方式修復帶寬開銷對比如圖4所示。

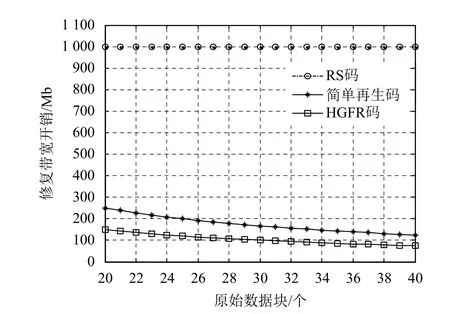
圖4 單節點故障時的修復帶寬開銷

當2 個節點發生故障時，若采用(n,k)RS 碼，仍然需要下載全部的原文件來修復故障節點，所以(n,k)RS 碼修復2 個故障節點的修復帶寬開銷仍為M；對于(n,k,f)SRC 簡單再生碼，如果2 個故障節點數大于f-1，則2 個節點發生故障的修復帶寬開銷為2(f+1)M/k，如果2 個故障節點數小于f-1，需要先恢復原文件，所以修復帶寬開銷為 M，這里f=4，所以2 個節點故障時，SRC 簡單再生碼的修復帶寬開銷為M；如果采用基于Hadamard 矩陣的分組FR 碼，2 個故障節點在同一修復組時，修復帶寬開銷為3M/k，不在同一修復組時，修復帶寬開銷為6M/k。修復帶寬開銷對比如圖5 所示。

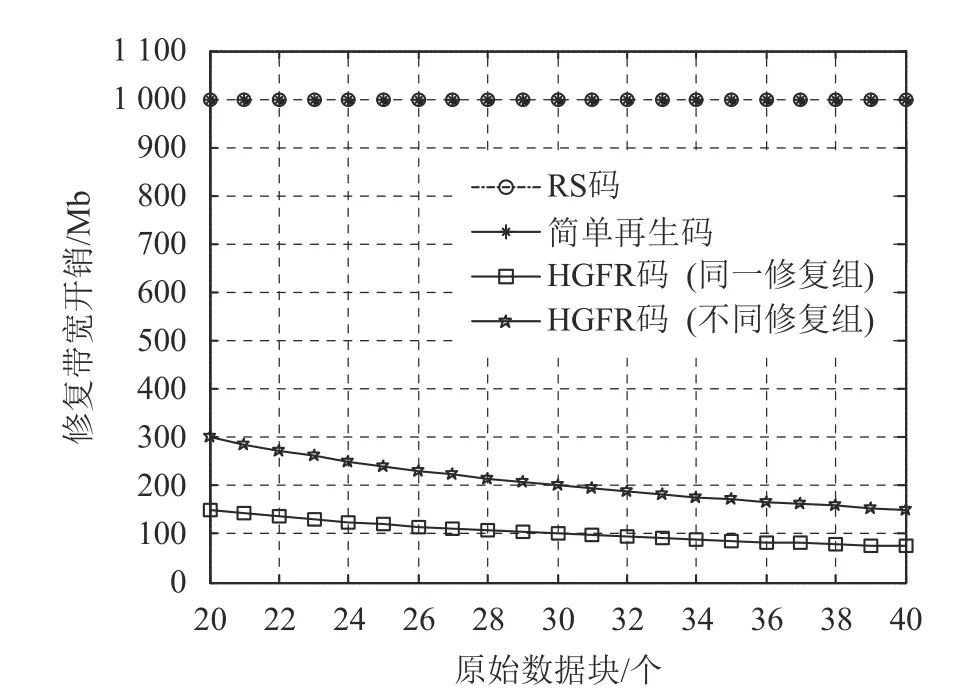
圖5 2 個節點故障時的修復帶寬開銷

從圖4 和圖5 可以看出，基于Hadamard 矩陣的分組FR 碼，單節點和兩節點故障時的修復帶寬開銷性能明顯優于RS 碼和SRC 簡單再生碼，且在圖5 中RS 碼和SRC 簡單再生碼由于修復帶寬開銷一樣，所以曲線重合。

4.2 修復局部性

修復局部性是指故障節點修復過程中需要連接的存活節點數目，即修復過程中的磁盤I/O 開銷。首先對于單節點失效，簡單再生碼修復時需要連接2 f個存活節點，所以局部修復性為 2 f；RS 碼發生單節點故障時，需要連接k個節點恢復原文件修復故障節點，所以RS 碼修復局部性為k；基于Hadamard矩陣的分組FR 碼，連接3 個未發生故障的節點來恢復單個節點故障，所以其修復局部性為3。單節點故障時的修復局部性對比如圖6 所示。

對于2 個節點發生故障，SRC 簡單再生碼需要先恢復原文件才可以修復故障節點，所以SRC簡單再生碼的修復局部性為k；對于RS 碼，仍然需要恢復原文件，所以修復2 個節點的修復局部性也為k；基于Hadamard 矩陣的分組FR 碼，分兩種情況：1) 如果一個修復組中發生2 個節點故障，從3 個未失效節點中下載所需數據，修復局部性為3；2) 2 個故障節點不在同一個局部修復組內，其修復兩個故障節點需要連接6 個存活節點，修復局部性為6。

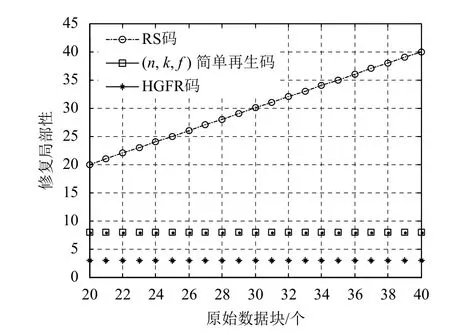
圖6 單節點故障時的修復局部性

修復故障節點時，可以看出基于Hadamard 矩陣的分組FR 碼的修復局部性，優于簡單再生碼和RS 碼的修復局部性。

4.3 修復復雜度

本文提出的基于Hadamard 矩陣的分組FR碼，當發生節點故障時，可以直接從其他存活節點下載數據塊進行修復，無需進行編碼運算。對于RS 碼修復故障節點需要先恢復原文件，之后再編碼生成所需要的數據塊，編碼數據塊由k個數據塊在有限域GF(q)上運算得到。所以RS 碼在修復單節點故障時需要k2+k次有限域乘法運算和k2-1次有限域加法運算。對于SRC 簡單再生碼，其修復一個故障節點需要進行(f-1)(f+1)次異或運算。可以看出，本文構造的FR 碼修復復雜度明顯低于RS 碼和SRC 簡單再生碼的修復復雜度，可以快速修復故障節點，修復時間減少。

表1 給出了分布式存儲系統中，RS 碼、簡單再生碼和基于Hadamard 矩陣的分組FR 碼分別在修復帶寬開銷、修復局部性及節點存儲開銷三方面的性能比較。從表1 可以看出，基于Hadamard 矩陣的分組FR 碼其修復局部性和帶寬開銷較低。而且，基于Hadamard 矩陣的分組FR 碼在修復節點故障時可以實現精確無編碼修復，運算復雜度較低，修復時間減少，可靠性提高。

5 結 束 語

現有傳統編碼方式對于故障節點的修復，特別是對多故障節點的修復，其修復帶寬開銷和修復局部性能受限，同時修復復雜度較高。為此，本文提出了基于Hadamard 矩陣的FR 碼，同時對其進行分組，運用8 階Hadamard 矩陣提出了分組FR 碼的一般性構造算法。理論分析發現，基于Hadamard矩陣的分組FR 碼可以對多故障節點進行快速精確無編碼修復，有效降低了運算復雜度，同時運用了分組可以實現組內修復，復雜度進一步降低。與RS 碼和SRC 簡單再生碼相比，發生故障時的修復局部性、修復復雜度和修復帶寬開銷進一步降低，且修復效率提高，減少了故障節點的修復時間。