基于重點域的自適應加點方法

毛 勇，曾 鋒，羅 曼

(武漢船舶通信研究所 武漢 430079)

復雜電子裝備通常涉及到機械、電磁、熱等多個學科，利用仿真軟件進行計算時，需要在多個學科間進行多次迭代，導致整體計算量偏大，計算效率低下。為減少仿真的計算量，提高計算效率，引入代理模型是必然的選擇[1]。多項式響應面、Kriging、徑向基函數、支持向量回歸等是常用的代理模型近似算法[2-3]。在實際應用中，利用Kriging模型進行設計的越來越多[4]。

通過加點方法不斷更新代理模型是提高代理模型預測精度的一種重要手段。文獻[5]提出的有效全局優化(efficient global optimization, EGO)算法是一種研究早且應用相對廣泛的加點方法。文獻[6]介紹了一種通過構造概率密度函數來選取新增樣本點的徑向基函數的追峰采樣(mode pursuing sampling,MPS)方法，該方法在進行高維問題優化時計算效率較低。文獻[7]提出一種集成最小化置信下限和信賴域(integrating minimize lower confidence bound and trust region, IMLCB-TR)的動態代理模型優化策略，該優化策略不僅能夠保證最優解精度，優化效率也有一定程度的提高。文獻[8]提出的一種基于智能空間探索的自適應響應面方法，該方法能夠在一定程度上提高計算效率，但是該方法的近似能力不理想，導致其在實際應用中可能陷入局部最優。

針對上述問題，本文提出了基于重點域的自適應加點方法(adaptive infilling method based on significant domain)。該方法在每次迭代時通過建立局部加點和全局加點模型以分別提高代理模型的局部開發能力和總體探索能力。最后，將本文提出的方法應用于標準數學測試問題和某共形天線的優化設計中，從數值結果上驗證本文方法的高效性和有效性。

1 基于重點域的自適應加點方法

基于重點域的自適應加點方法的基本思想為：利用空間縮放技術確定重點域，然后基于重點域建立局部加點模型以提高近似方法的局部開發能力，同時利用平衡變量和設計點的預測方差建立全局加點模型，提高近似方法的總體探索能力。

1.1 局部加點模型

為了提高近似方法的局部開發能力，在重點域的基礎上，本文提出了一種局部加點方法，數學模型如下：

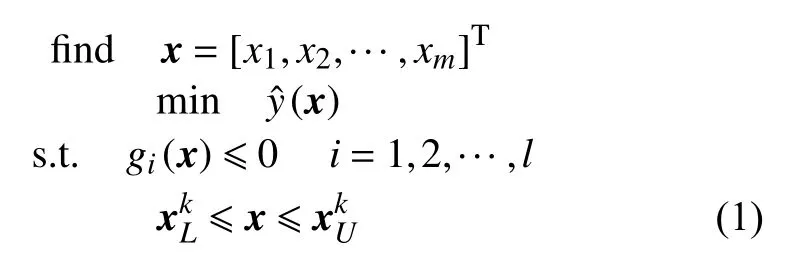
式中，中心點的更新方法如下：

取樣范圍的長度更新方法為：

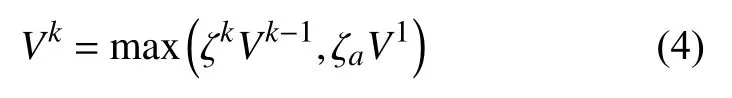
式中，Vk-1為第k-1次迭代得到的取樣范圍的長度值； V1為初始設計區間的長度。在迭代時，有可能會出現重點域長度過小而出現新增樣本點在某一區域過于集中的問題，因此可給定最小重點域的長度ζaV1，參數 ζa可以根據實際情況選取。控制因子ζk的更新方法為[8]：

式中， εa為代理模型的容許精度，本文利用當前最優解的相對誤差ε來估計當前近似方法的預測精度：

xk-1k-1式中，的取值為第次迭代時響應值最小的樣本點。

1.2 全局加點模型

最大化Kriging 模型給出的設計點預測方差可以提高近似方法的全局預測精度，但是在實踐中獲得預測方差的最大值非常難，從而導致其性能改善程度有限。因此本文提出通過平衡變量和設計點的預測方差來綜合確定設計空間中不確定性較大的區域，以提高模型的總體探索能力。數學描述為：

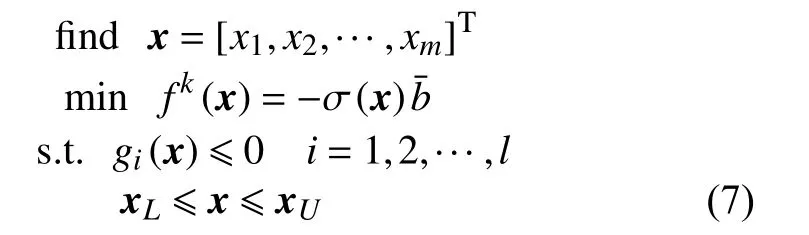
1.3 方法的實現流程

圖1 為本方法的流程圖，優化過程中的相關參數計算如下：

1)本文采用maximin 準則選取初始樣本點，迭代次數設定為1 000。初始樣本點個數同設計變量的個數m 有關，參考文獻[10]中的選取辦法：

2)當包含有耗時約束時，利用文獻[8]中的自適應罰函數方法進行約束處理，然后利用Kriging建立功能函數的代理模型。

3)收斂條件判斷。當實際分析模型的計算次數達到設定的最大次數或連續兩次迭代得到的最優解相對誤差 Δ小于給定的收斂標準 Δa時，如式(10)所示，則停止迭代。

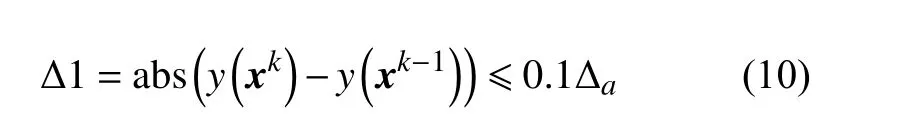
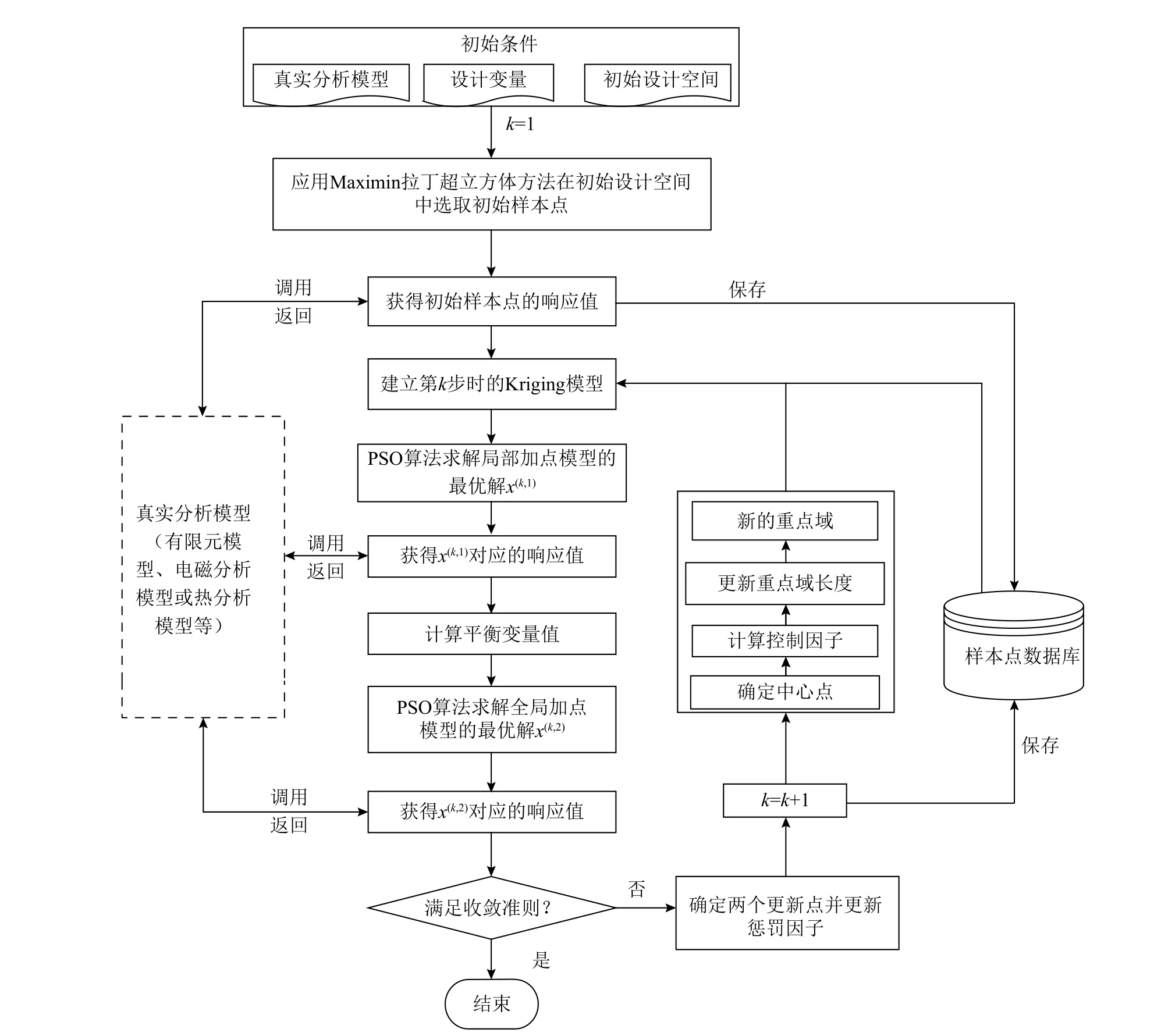
圖1 本方法的流程圖

2 測試算例

為了驗證本文方法的有效性，特選取BR、SE、PK、SC、GN、HN6 等作為低維函數測試算例，選取R10、HD1、F16 等作為高維函數測試算例，以驗證本文方法對不同維度問題的求解能力，表1為所有測試函數的相關信息，測試函數來源見文獻[8]。

BR 函數表達式為：

表1 測試函數的相關信息

SE 函數表達式為：

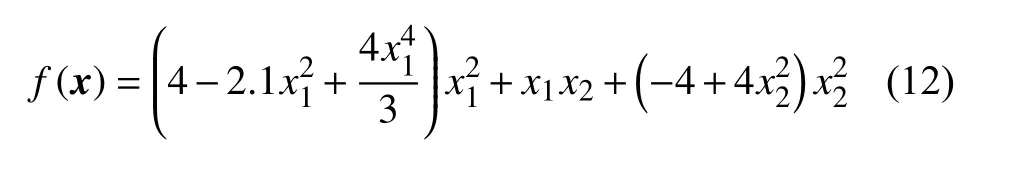
PK 函數表達式為：

SC 函數表達式為：

Hartmann 函數系列表達式為：

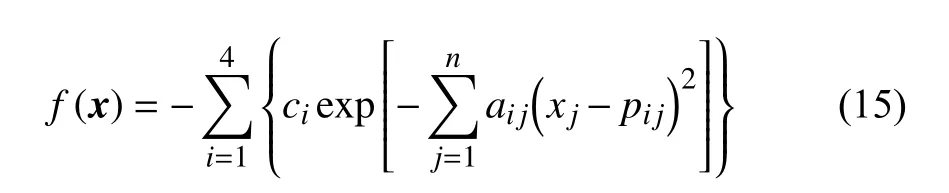
當n=6時，對應為Hartmann6 函數，此時系數a,p,c的取值參見文獻[8]。

GN 函數表達式為：

R10 函數表達式為：

HD1 函數表達式為：

F16 函數表達式為：

將本文方法同文獻[5]中的EGO、文獻[6]中的MPS 和文獻[8]中的ARSM-ISES 方法進行對比。本文方法中Δa=0.005，εa=0.01， ζa=0.05，優化方法選用PSO，PSO 采用Brain Bridge 教授開發的工具箱，PSO 中種群個體數24、加速度參數為2、初始時的權值為0.9、結束時的權值為0.4，其他參數為工具箱中默認值。從理論上來說，EGO方法也可以用來求解高維函數的優化問題，但是由于EGO 方法的收斂速度慢，對于高維函數計算量過大，因此，高維函數中EGO 方法不做比較，后3 種方法的測試結果見文獻[8]。為了保證優化結果的可靠性，在優化時需利用每種方法對每個測試函數連續優化10 次，每種方法得到的最終優化結果取10 次優化的中位值，表1 給出了測試函數的優化結果和最優解變化范圍的對比，以綜合評估幾種方法的全局和局部預估能力及方法的穩健性。表2 給出了測試函數模型調用次數的平均值和其變化范圍，以評估不同方法的優化效率。

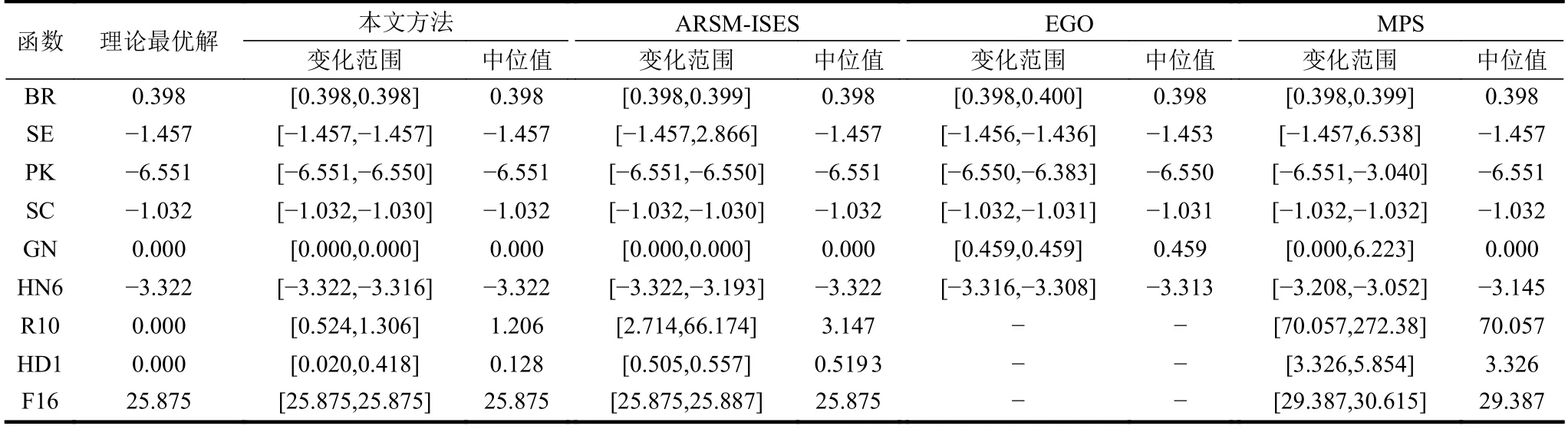
表2 測試函數的優化結果和最優解變化范圍的對比

由表2 可知，對于大部分的低維測試函數，本文方法和ARSM-ISES 方法都能得到測試函數的理論最優解。對于GN 函數，EGO 方法所得優化結果同理論最優解相差較大，對于HN6 函數，MPS方法的結果同理論最優解有一定差距。針對高維函數，本文方法所得的優化結果同理論最優解最為接近，而且模型調用次數是幾種方法中最少的，ARSMISES 其次，MPS 所得最優解最差。

模型調用次數是一種重要的表征代理模型優化效率的度量標準。由表3 可知，對于大部分測試函數，本文方法所用次數最少。對比于ARSM-ISES方法，兩種方法雖然都引入了空間縮減技術進行模型管理，但由于本文方法中的代理模型使用的是近似能力更高的Kriging 模型，所以其優化效率和預測精度均有所提高。對于低維測試函數，雖然EGO 有著更高的優化效率，但其最優解對比于其他方法卻是最差的。對于部分測試函數，MPS 的最小模型調用次數比本文方法都少，但是從表2 可以看出，引起這種情況的原因可能是由于MPS 方法提前收斂于局部最優解。

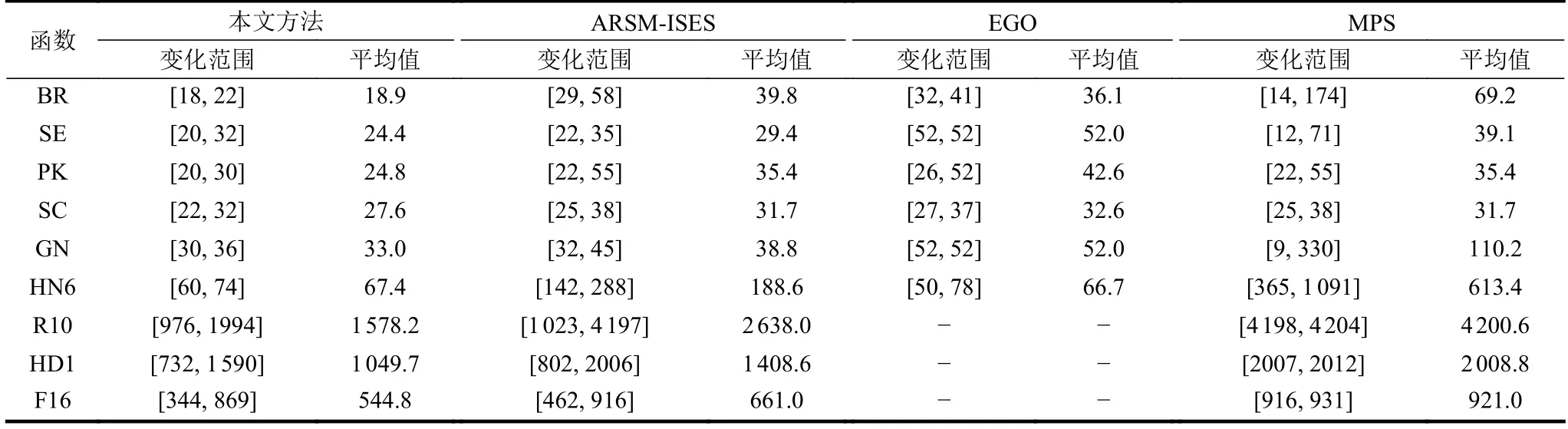
表3 測試函數的模型調用次數平均值和變化范圍的對比

由上述對比可知，對于高維和低維問題，本文方法在計算效率和全局收斂性能方面上都有優勢，有廣闊的應用前景。

3 共形天線優化設計實例

共形天線作為武器平臺的蒙皮結構，已經廣泛應用到新一代戰機、無人機、預警飛艇的機翼、機腹或機背等結構中[11]。圖2 為該類型天線的基本結構，其中面板和蜂窩層具有力學承載功能，射頻功能層實現電磁波的發送和接收，它主要由微帶輻射單元陣列和對應的微波電路組成。

圖2 共形天線的結構組成示意圖

以天線的蜂窩層厚度 d1、上下面板層厚度 d2、蜂窩胞元壁厚 d3和蜂窩胞元壁長 d4為設計變量，長度單位都為mm，假設天線承受載荷為8 000 N，分析軟件為ANSYS 和Matlab，最小化天線質量W，約束為天線的應力約束和位移約束。此時，建立的優化模型為：

對于該優化問題，根據文獻[11]的建議，本文中σmax=110 MPa，δmax=5 mm。將本文方法、EGO方法和PSO 方法(目標和約束都使用實際模型)對比，優化方法以及結果的選取方法同測試算例一致，所得結果如表4 所示。

表4 優化結果對比

由表4 可知，PSO 方法所得結果最優，但是其計算量也最大。本文方法優化結果優于EGO 方法，且模型調用次數比其他兩種方法都少。上述結果表明本文方法具有較好的實際應用能力。

4 結 束 語

針對復雜電子裝備產品優化設計過程中計算量較大的問題，提出了基于重點域的自適應加點方法，在每次迭代時建立的全局加點和局部加點模型可以兼顧總體探索和局部開發。在局部加點模型中引入重點域可以提高局部開發的搜索效率和優化的收斂性，在全局加點模型中基于已有樣本點信息建立的平衡變量可以提高Kriging 模型的全局預測精度。標準的測試函數算例和某共形天線優化設計的結果表明，同其他幾種方法相比，本文方法不僅具有較高的全局收斂性，同時計算效率也有了很大的提升。在未來的研究中可將本方法應用于更多復雜的電子裝備的優化設計中，并進一步探索更加高效的加點方法。