一種基于代價函數的跳頻周期估計算法

周德強，白雪飛，尤少欽，閆紅超

(1. 河北省電磁頻譜認知與管控重點實驗室，河北 石家莊 050081；2.中國人民解放軍32090部隊，河北 秦皇島 066000)

0 引言

跳頻通信具有較強的抗多徑、抗衰落、抗干擾和截獲概率低等諸多優點，在軍事通信領域獲得廣泛應用，因此對跳頻信號的偵察成為通信對抗的主要領域之一。在跳頻通信偵察中，跳頻周期是一個重要參數，為了實現網臺分選[1]，需要對跳頻周期進行精確估計。目前的跳頻周期估計算法主要有3類：① 脈沖重復周期(Pulse Repetition Interval，PRI)[2-3]直方圖類算法，包括CDIF算法、SDIF算法及其改進算法[4-5]，這些算法也常用于雷達信號分選中；② PRI變換法及其改進算法[6-9]，這些算法同樣也常用于雷達信號分選中；③ 對跳頻信號進行時頻分析[10-13]，提取跳頻信號時頻分布的峰值序列、時頻脊線等特征[14-15]，利用這些特征的周期性估計跳頻周期[16-19]。PRI直方圖類算法在跳頻信號丟失率低并且跳頻信號到達時間抖動很小的情況下估計效果較好。但在實際工程應用中，受限于時間分辨率，跳頻信號的到達時間抖動很難控制到很小，在復雜電磁環境下跳頻信號的丟失率也不能保證很低，因此PRI直方圖類算法使用范圍受限[4]。PRI類算法對到達時間進行PRI變換處理，通過在PRI譜圖上搜索譜峰來估計跳頻周期，該類算法在到達時間抖動較大時估計性能較差[7]。時頻分析類算法通過提取跳頻信號時頻分布中的峰值序列、時頻脊線等的周期來估計跳頻周期，不能適應電磁環境中存在多網臺的復雜情況[18-19]。

針對以上跳頻周期估計算法中存在的問題，本文提出了一種基于代價函數的跳頻周期估計算法，以相對到達時間的直方圖統計的方差作為代價函數[20]，代價函數最大值所對應的自變量即為跳頻周期估計值。該算法不僅估計精度高，而且適應多網臺存在的復雜電磁環境。

1 問題模型

對于通信偵察方，同一個電臺發射的跳頻信號的到達時間可以建模為一個等差數列，數列的公差是跳頻周期。因此，第i個電臺的第j跳信號的到達時間可以表示為：

ti,j=kiTi+toi+jTi，

(1)

式中，i=0,1,2,…；j=0,1,2,…；Ti是第i個電臺的跳頻周期；toi是取值范圍為[0,Ti)的常量；ki是整數。跳頻周期估計問題其實是已知跳頻信號的一系列到達時間ti,j，求解跳頻信號的跳頻周期Ti。對于不同跳速的跳頻信號，可以根據跳頻信號的駐留時間將其區分開，因此跳頻周期估計問題可以簡化為：已知同一跳速的跳頻信號的一系列到達時間ti,j，估計跳頻周期T，其中ti,j可以表示為：

ti,j=kiT+toi+jT。

(2)

2 算法原理

假設未知的跳頻周期為變量x，跳頻信號的相對到達時間可以表示為：

(3)

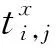
構造代價函數：

(4)

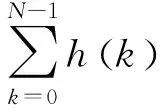
(5)

對于非負實數a，b，有：

(a+b)2=a2+b2+2ab≥a2+b2。

(6)

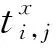
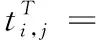
(7)

可見，此時每個網臺的跳頻信號的相對到達時間都變成了常量，分布的比較集中，直方圖統計的方差最大，即代價函數J(x)最大。因此，跳頻周期的估計值可以表示為：

(8)

式中，TL，TH是根據經驗或者跳頻周期粗估計算法確定的搜索范圍的上、下限。

3 算法實現

本文采用搜索的方式實現基于代價函數的跳頻周期估計算法，在[TL,TH]上以Δx為步長計算可能的跳頻周期xk=TL+kΔx對應的代價函數值J(xk)，最大函數值對應的自變量即為跳頻周期的估計值，具體步驟如下：

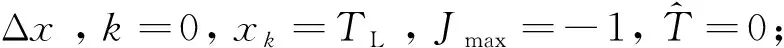
情況 3 v9不染1, 不失一般性,假設它染3,則可用上述的方法將窮點v1,v5的顏色2改染為顏色1, 并用2 來染v。

② 根據式(3)和式(4)計算J(xk)；

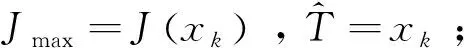
④ 更新k：k=k+1；

⑤ 計算xk：xk=TL+kΔx；

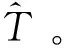
在實際實現中，可以采用變步長的搜索方法減少計算量[20]。

4 性能分析

(9)

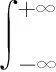
(10)

5 仿真試驗

5.1 算法驗證

算法中的搜索步長設置為1 μs，直方圖統計的箱長設置為5 μs，搜索范圍設置為900 ～1 100 μs。試驗數據是在外場利用短時傅里葉變換檢測到的3個電臺的20 007跳信號的到達時間，短時傅里葉變換的時間分辨率為44.444 μs，3個電臺的跳頻周期均為1 ms，計算出的代價函數示意如圖1所示。由圖1可以看出，代價函數的最大值出現在1 ms處，該值等于跳頻周期的真值，驗證了算法的有效性。

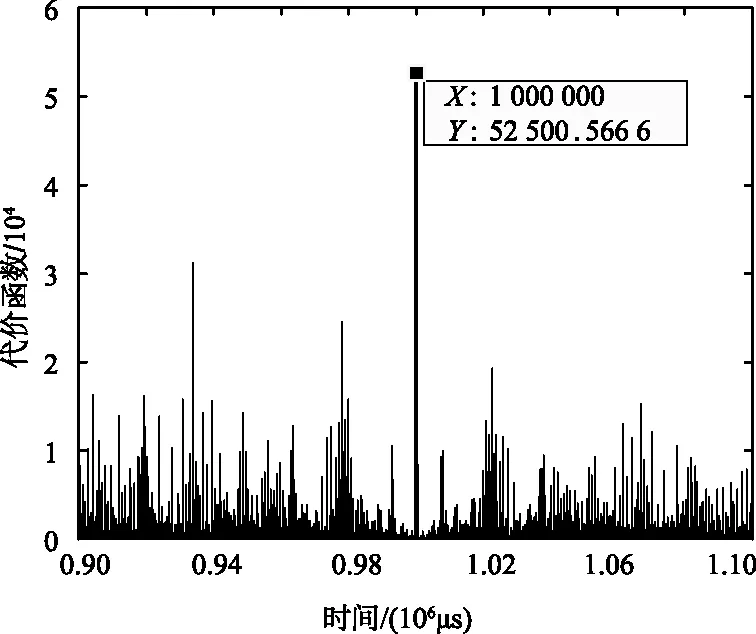
圖1 代價函數示意Fig.1 Schematic diagram of cost function

5.2 搜索步長對算法性能的影響

本小節驗證了搜索步長對算法性能的影響。在仿真中，搜索步長設置在1～19 μs之間，每種步長下進行1 000次蒙特卡羅仿真，每次處理3個1 000跳/秒的跳頻電臺的10 000跳信號。算法中直方圖統計的箱長設置為5 μs，搜索范圍是900～1 100 μs。仿真結果如圖2所示。當搜索步長分別設置為1 μs和5 μs時，歸一化均方誤差其實是0，為了避免對0取對數，對所有的歸一化均方誤差都加了1×10-21。由圖2可以看出,歸一化均方誤差并不是隨著搜索步長的增加而嚴格增加的,這是因為當搜索步長和搜索范圍的起始值設置的恰好合適時，即使搜索步長較大，也可能恰好搜索到真實的跳頻周期，此時歸一化均方誤差較小。以本仿真為例，當搜索步長取5 μs時，900 μs+5 μs×20 = 1 000 μs，恰好能搜索到真實的跳頻周期，歸一化均方誤差為0。當搜索步長取3 μs時，900 μs+3 μs×33 = 999 μs，900 μs + 3 μs×34=1 002 μs，可見此時不能搜索到真實的跳頻周期，所以即使其搜索步長比5 μs小，但是歸一化均方誤差比5 μs時大。當跳頻周期未知時，從統計角度上看，越小的搜索步長搜索到真實跳頻周期的概率越大，歸一化均方誤差越小，因此在計算速度可容忍的情況下應該盡量減小搜索步長。

圖2 不同搜索步長下的歸一化均方誤差Fig.2 Mean square error of normalized hopping cycle versus different search steps

5.3 丟跳適應性驗證

考慮到在復雜電磁環境中存在丟跳情況，本小節驗證了算法的丟跳適應性，并與文獻[8]中的PRI變換法進行了對比。在仿真中，丟跳率設置在0～0.5之間只有一個500跳/秒的跳頻電臺，每種丟跳率下進行1 000次蒙特卡羅仿真，每次處理10 000跳信號。本文算法中的搜索步長設置為13 μs，直方圖統計的箱長設置為5 μs，搜索范圍是1 900～2 100 μs。PRI變換法的箱長設置為13 μs，搜索范圍是1 900 ～2 100 μs。仿真結果如圖3所示。由圖3可以看出，本文算法和PRI變換法對丟跳率都不敏感，本文算法的性能略好于PRI變換法。

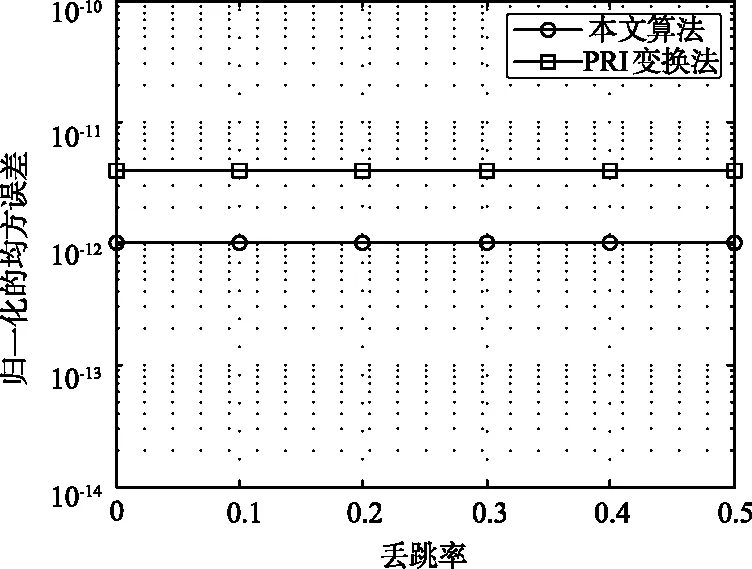
圖3 不同丟跳率下的歸一化均方誤差Fig.3 Mean square error of normalized hopping cycle versus different data loss rates

6 結束語

本文提出了一種基于代價函數的跳頻周期估計算法，從理論上推導了算法的合理性，利用外場數據驗證了算法的正確性，通過仿真試驗驗證了搜索步長對算法的影響和算法對丟跳率的不敏感性。通過選擇合適的搜索步長，跳頻周期估計值的歸一化均方誤差可以達到0。本算法不僅估計精度高，而且魯棒性強，對于網臺分選的工程實現具有重要意義。