一種PolSAR圖像G0分布參數估計新方法

崔浩貴，晏 慶，張 曉，楊 飛，范路芳

(中國人民解放軍91001部隊，北京 100841)

0 引言

極化合成孔徑雷達(Polarimetric Synthetic Aperture Radar，PolSAR)雜波統計建模及其參數估計方法是PolSAR圖像相干斑抑制[1]、分類識別[2-3]和目標檢測[4]等圖像解譯手段的重要課題。在PolSAR圖像中，均勻區域一般用高斯模型進行建模，而非均勻區域常用多變量乘積模型來進行非高斯建模。多變量乘積模型將PolSAR復散射向量表示為一個紋理分量和一個服從復高斯分布的相干斑分量的乘積，并且二者之間相互統計獨立。G0分布模型[5-6]是應用非常廣泛的PolSAR圖像非高斯統計模型，它是在假設紋理分量服從逆Gamma分布時根據多變量乘積模型得到的。G0分布模型特別適用于城區等極不均勻區域的統計建模。

尋找快速、準確的參數估計是G0分布模型研究的核心問題。根據采用的數據源，可將G0分布參數估計方法分為單極化估計方法和全極化估計方法。其中傳統的單極化估計方法分別估計出每個極化通道的參數，然后將各通道的參數求平均。而全極化估計方法利用了各通道之間的極化信息，其估計性能優于單極化的方法。目前最常用的全極化估計方法是Anfinsen等提出的基于協方差矩陣的對數累積量(Matrix Log Cumulants，MLC)的參數估計方法，該方法本質上是協方差矩陣行列式值的Mellin變換[7-11]。最近，Khan等人[12]將基于多視極化白化濾波器(Multilook Polarimetric Whitening Filter，MPWF)的參數估計方法擴展到分數階矩(Fractional Moments，FM)的情形，提出了基于多視極化白化濾波器分數階矩(MPWF-FM)的參數估計方法。實驗結果表明，該方法比MLC方法具有更小估計方差和均方誤差(Mean Square Error，MSE),但是該方法存在計算復雜、最優的分數階矩無法理論推導得到和當紋理參數較小時失效等問題。

本文提出了一種基于多視極化白化濾波器對數累積量(Log Cumulants of MPWF，MPWF-LC)的參數估計新方法。新方法解決了MPWF-FM方法存在的估計失效等問題，并且具有更優的估計性能。通過G0分布數據和實測數據分別進行了仿真分析，結果有效驗證了新方法的參數估計結果準確度高、計算速度快。

1 PolSAR圖像乘積模型

PolSAR系統在測量中獲取的信息可用復散射向量k表示：

k=[Shh,Shv,Svh,Svv]T，

(1)

式中，[·]T表示向量的轉置；Sxy表示發射極化方式為x，接收極化方式為y的復散射系數；h表示水平極化；v表示垂直極化。

多變量乘積模型常用來對PolSAR圖像進行非高斯建模，它將復散射向量表示為相互統計獨立的紋理分量τ和相干斑分量y的乘積，即：

(2)

式中，y服從復高斯分布，其概率密度函數為：

(3)

式中，d是復高斯矢量的維數；Γ=E{yyH}，E{·}表示隨機變量的數學期望。

實際中，為了抑制相干斑，常對圖像進行多視處理，其過程可表示為：

(4)

式中，L為視圖數，L≥d；上標“H”表示共軛轉置；l代表第l個像素點。假設進行多視處理的像素點具有相同紋理分量，此時式(4)可簡化為：

C=τY，

(5)

其中，

(6)

式中，Y服從Wishart分布，其概率密度函數為：

(7)

式中，d是Y的維數；Γ=E(Y)；Tr(·)表示矩陣的跡；函數Γd(L)為復數形式的多變量伽馬函數：

(8)

式中，Γ(·)為標準Eular伽馬函數。由于這里假設在多視窗口內紋理分量恒定，樣本的協方差矩陣可表示為：

Σ=E{C}=E{τ}E{Y}=E{τ}Γ。

(9)

當式中紋理分量服τ為逆伽馬分布，即τ～γ-1(u,α)時，其乘積模型服從G0分布。

2 基于MPWF對數累積量的參數估計方法

MPWF濾波器通過最優地組合極化協方差矩陣中的所有元素，得到一幅降斑的圖像[13-14]。進行MPWF濾波后的數據可表示為：

(10)

將式(5)和式(9)代入式(10)，MPWF濾波后的數據可分解為：

(11)

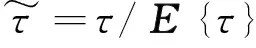
x～γ(d,Ld)，

(12)

其中，伽馬分布γ(u,d)的概率密度分布函數為：

(13)

基于Mellin變換的對數累積量定義為：

(14)

式中，kr{z}表示隨機變量z的第r階對數累積量；E{zs-1}為關于隨機變量z的數學期望。當隨機變量服從如式(11)所示的乘積模型時，其對應的對數累積量為加性模型[8]：

(15)

由于隨機變量x服從如式(12)所示的伽馬分布，可得其對數累積量為：

(16)

式中，ψ(x)=Γ′(x)/Γ(x)為digamma函數；Γ(x)為伽馬函數。ψ(m,x)表示m階Polygamma函數：

(17)

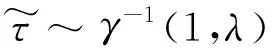
(18)

將式(16)、式(18)代入式(15)，可得基于MPWF對數累積量(MPWF-LC)的G0分布參數估計方法為：

(19)

(20)

3 仿真結果與分析

用G0分布仿真數據比較以下幾種方法的相對估計偏差、相對估計方差、相對MSE和計算時間：

① MPWF-FM[12]；

② MLC方法，取二階MLC進行參數估計[8]；

③ 本文提出的MPWF-LC參數估計方法，取二階對數累積量的表達式，即在式中取r=2。

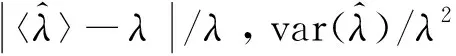
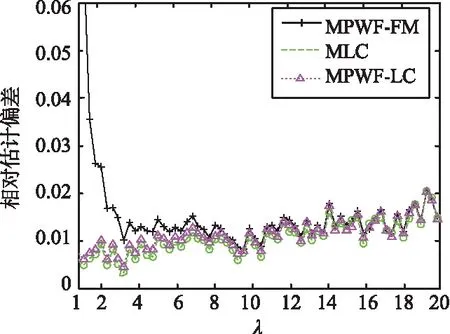
(a)相對估計偏差

圖1 G0分布情形，不同參數λ下3種估計方法的相對估計偏差、相對估計方差與相對MSEFig.1 The relative estimation bias, relative estimation variance and relative MSE for three estimation methods with different parameters of λ in the case of G0 distribution

G0分布下各估計方法在不同樣本數下的計算時間如圖2所示。

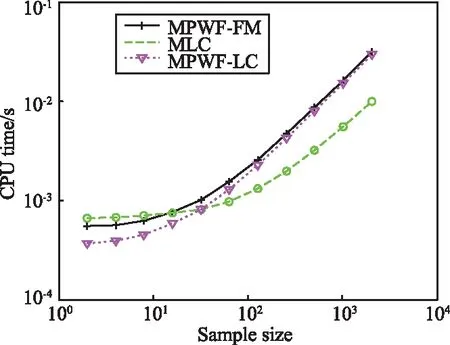
圖2 各估計方法的計算時間比較Fig.2 Comparison of calculation time of different estimation methods

仿真數據參數L=10，λ=10。采用Matlab進行編程計算，計算機CPU為Intel E5700，雙核3 GHz，內存大小2 GB。由圖2可以看出，當樣本數較小時，MPWF-LC計算所花的時間最短，計算復雜度最低；隨著樣本數的增加，當樣本大于100后，MLC具有最短的計算時間；另外，在任意樣本數下，MPWF-FM所需的計算時間最長。

4 實測數據分析

用實測數據對MPWF-LC，MPWF-FM和MLC三種方法進行分析。選取的實測數據為AIRSAR系統于1989年獲得的Flevoland地區L波段PolSAR圖像(12.1 m×6.7 m)，以及1988年獲得的San Francisco地區的L波段PolSAR圖像(10 m×10 m)。對原始數據進行了L=4(2×2)的多視處理，由于Flevoland地區的數據源為4視數據，因此其視圖數變為L=16。

采用基于對數累積量的假設檢驗方法對實測數據進行擬合分析。簡單假設檢驗情形下，統計量Qp可表示為：

Qp=n(〈k〉-k)TK-1(〈k〉-k)，

(21)

式中，〈k〉為樣本的MLC，k為特定模型下MLC的理論值；n為樣本數；下標p為〈k〉或k的維數，K=nE{(〈k〉-k)(〈k〉-k)T}。可知Qp服從自由度為p的χ2分布[15]：

Qp→χ2(p)。

(22)

假設檢驗中的概率值(Probability Value，p值)是指在由H0所規定的總體中隨機抽樣，獲得等于及大于現有統計量的概率。由上述分析可知，p值可由統計量Qp根據χ2(p)分布計算得到。在參數估計中視圖數L用名義視圖數代替，向量〈k〉和k采用2階和3階MLC，即〈k〉=[〈k2〉,〈k3〉]T，k=[k2,k3]T。

在2幅圖像中各選取了4個大小為20 pixel×20 pixel的區域進行參數估計與假設檢驗，比較各參數估計方法在G0分布假設下的p值。圖3和圖4分別給出了2幅圖像中4個區域的選擇以及各區域的樣本對數累積量〈k〉。如圖3(a)所示，Flevoland圖像中選取的4個區域分別為河流、森林、小麥和油菜籽區域[16]。由圖3(b)可知，河流的MLC靠近G0分布，森林的MLC靠近K分布，而小麥和油菜籽區域與Wishart、K和G0分布都非常接近。如圖4(a)所示，San Francisco圖像中選取的4個區域分別為海洋、城區、植被1和植被2。由圖4(b)可知，海洋的MLC靠近Wishart分布，城區的MLC靠近G0分布，而植被1和植被2靠近K分布。

(a)4個區域的示意(Pauli RGB圖像)

(a)4個區域的示意(Pauli RGB圖像)

Flevoland四個區域在G0分布模型下的參數估計結果及假設檢驗p值如表1所示。由表1可以看出，對于河流區域，所有估計方法得到的p值都能通過顯著性水平α=0.05的假設檢驗，但是MLC方法的p值最大。對于小麥和油菜籽區域，所有估計方法的p值都較大。森林區域同樣地無法通過顯著性水平α=0.05的假設檢驗。

表1 Flevoland四個區域在G0分布模型下的參數估計結果及p值

San Francisco四個區域在G0分布模型下的參數估計結果及假設檢驗p值如表2所示。由表2可以看出，對于城區，只有MLC方法的p值都能通過顯著性水平α=0.05的假設檢驗，其他2種方法p值很小。對于海洋區域，3種方法的結果都能通過顯著性水平α=0.05的假設檢驗，但是MLC方法的p值略小。植被1和植被2區域，所有估計方法的p值都無法通過顯著性水平α=0.05的假設檢驗。

表2 San Francisco四個區域在G0分布模型下的參數估計結果及p值

從上述分析可以看出，MPWF-LC和MPWF-FM方法的參數估計結果和p值都非常接近。而MLC方法在某些區域表現較好，例如Flevoland圖像中的河流和San Francisco圖像中的植被2區域，這是因為該參數估計方法和假設檢驗都是基于MLC。在其他區域，MLC方法和另外2種方法的結果也基本上相差不大。從該結果可以看出，本文提出的MPWF-LC方法在實測數據參數估計中的有效性。

5 結束語

以多視極化白化濾波器和對數累積量為基礎，提出了基于多視極化白化濾波器對數累積量的G0分布模型的參數估計方法。用仿真數據和實測數據對本文方法與MLC方法以及MPWF-FM方法進行了比較。實驗結果表明，本文方法具有最小的估計方差和MSE，并且在樣本數較少時，計算時間最短。另外，可以將本文方法應用于Fisher分布、U分布等PolSAR圖像模型，其推導結果及估計效果值得研究。