基于強(qiáng)度折減法的某水利工程邊坡靜動(dòng)力穩(wěn)定性分析

郭澤宇,許戰(zhàn)軍，張 帆

(中國(guó)電建集團(tuán)西北勘測(cè)設(shè)計(jì)研究院有限公司,西安 710065)

0 前 言

自強(qiáng)度折減法提出以來(lái)，許多學(xué)者基于強(qiáng)度折減法對(duì)巖土結(jié)構(gòu)的靜力及動(dòng)力穩(wěn)定性問題進(jìn)行了研究。如陶宇等[1]研究了傳統(tǒng)的邊坡失穩(wěn)三大判據(jù)在二維均質(zhì)和非均質(zhì)邊坡中的適用性問題。王曼等[2]結(jié)合關(guān)鍵點(diǎn)位移突變判據(jù)和塑性區(qū)貫通判據(jù)，分析了某邊坡從局部到整體的失穩(wěn)過(guò)程。李庶林等[3]分析了高陡邊坡加固前后的穩(wěn)定性問題，結(jié)果表明：使用預(yù)應(yīng)力錨索、錨桿等加固措施后，能有效提升邊坡的穩(wěn)定性。江衛(wèi)華等[4]分析了三維邊坡的穩(wěn)定性，并與極限平衡法的結(jié)果進(jìn)行對(duì)比，驗(yàn)證了強(qiáng)度折減法在三維邊坡中的適用性。趙旭等[5]對(duì)地震作用下的隧道洞口的穩(wěn)定性進(jìn)行了分析。江德軍等[6]對(duì)比研究了強(qiáng)度折減法等5種方法在邊坡抗震分析中的適用性問題，結(jié)果表明：動(dòng)力有限元強(qiáng)度折減法與有限差分強(qiáng)度折減法計(jì)算出的邊坡安全系數(shù)接近，但在不同折減系數(shù)下的關(guān)鍵點(diǎn)位移差異性較大。本文使用有限元軟件ADINA，基于強(qiáng)度折減法對(duì)國(guó)內(nèi)某水利工程右岸邊坡在靜力及動(dòng)力作用下的穩(wěn)定性進(jìn)行了分析。

1 計(jì)算理論與方法

1.1 強(qiáng)度折減法

強(qiáng)度折減法把邊坡現(xiàn)狀抗剪強(qiáng)度參數(shù)(c、φ)等比例折減k倍，然后用折減之后的邊坡抗剪強(qiáng)度參數(shù)(c1、φ1)進(jìn)行穩(wěn)定性分析，計(jì)算公式如下：

(1)

定義使邊坡達(dá)到臨界失穩(wěn)狀態(tài)時(shí)對(duì)邊坡抗剪強(qiáng)度參數(shù)(c、φ)的折減程度k為安全系數(shù)。

1.2 邊坡失穩(wěn)判據(jù)

邊坡失穩(wěn)判據(jù)主要有計(jì)算不收斂判據(jù)、位移突變判據(jù)和塑性區(qū)貫通判據(jù)。為確保計(jì)算結(jié)果的準(zhǔn)確性，本文綜合考慮關(guān)鍵點(diǎn)的位移及塑性區(qū)的分布情況,對(duì)邊坡的靜力及動(dòng)力的穩(wěn)定性進(jìn)行分析。

2 工程實(shí)例

2.1 工程概況

國(guó)內(nèi)某水利工程壩址區(qū)右岸邊坡永久性坡高68 m左右，開挖前平均坡腳27°，開挖后坡腳為38.7°，開挖后分設(shè)5級(jí)馬道。邊坡巖體主要為千枚巖，由表及里共分全夾強(qiáng)風(fēng)化帶、強(qiáng)風(fēng)化帶以及弱風(fēng)化帶3個(gè)分帶。經(jīng)監(jiān)測(cè)資料分析，邊坡穩(wěn)定性較差，淺表層巖體易發(fā)生滑動(dòng)。邊坡工程地質(zhì)剖面如圖1所示。

圖1 邊坡工程地質(zhì)剖面圖 單位：m

2.2 邊坡有限元模型的建立

合理的有限元邊界范圍設(shè)定會(huì)使仿真結(jié)果與工程實(shí)際結(jié)果更為接近，鄭穎人[7]經(jīng)對(duì)比分析得出：坡腳至左邊界距離、坡頂至右邊界距離分別取坡高H的1.5倍、2.5倍，上下邊界距離不低于坡高的2倍計(jì)算結(jié)果較為合理。本文坡高H=68 m，因此，坡腳至左邊界距離、坡頂至右邊界距離、上下邊界距離分別取103 m、171 m、136 m。采用有限元軟件ADINA建立邊坡二維有限元模型，邊坡采用Mohr-Coulomb屈服準(zhǔn)則，網(wǎng)格劃分如圖2所示，巖土體具體物理力學(xué)參數(shù)如表1所示。

圖2 邊坡有限元模型圖

(1) 靜力工況下僅考慮自重的作用，模型底部和四周分別采用全約束和鏈桿約束；

(2) 動(dòng)力工況下考慮自重和地震荷載的作用，在底部及四周設(shè)置等效一致粘彈性邊界[8]，以真實(shí)反映遠(yuǎn)域地基輻射阻尼對(duì)地震波的影響，地震波從底部輸入。

表1 巖體材料物理力學(xué)參數(shù)表

本文基于NB 35047-2015《水電工程水工建筑物抗震設(shè)計(jì)規(guī)范》反應(yīng)譜[9]，以及阻尼比5%、動(dòng)力放大系數(shù)βmax=2.5合成一組水平向峰值加速度為0.2g和豎向峰值加速度為0.133g人造地震波。人造波持時(shí)20 s，計(jì)算步數(shù)為2 000，步長(zhǎng)0.01 s，地震加速度時(shí)程曲線如圖3所示。

圖3 地震加速度時(shí)程曲線圖

2.3 靜力工況分析

圖4為靜力工況下坡頂關(guān)鍵H水平向位移與折減系數(shù)的關(guān)系曲線。可以看出，當(dāng)折減系數(shù)k=1～2.4時(shí)，隨著折減系數(shù)的增加，坡頂關(guān)鍵點(diǎn)H的水平向位移增速緩慢；當(dāng)折減系數(shù)k>2.4時(shí)，隨著折減系數(shù)的增加，坡頂關(guān)鍵點(diǎn)H的水平向位移明顯增加。從位移突變的角度，可以認(rèn)為在靜力工況下，當(dāng)折減系數(shù)達(dá)到2.4時(shí)，邊坡正處于臨界失穩(wěn)狀態(tài)。

圖5為靜力工況時(shí)不同折減系數(shù)下的邊坡塑性區(qū)分布圖。隨著折減系數(shù)的增大，巖土材料在不斷軟化，塑性區(qū)從邊坡最薄弱的地方慢慢開展直至貫通。當(dāng)k=1.9時(shí)，塑性區(qū)主要產(chǎn)生于2號(hào)強(qiáng)風(fēng)化巖部分，隨著k的不斷增大，塑性區(qū)慢慢向坡頂及1號(hào)全夾強(qiáng)風(fēng)化巖部分?jǐn)U展；當(dāng)k=2.4時(shí)，塑性區(qū)延伸到坡頂，邊坡產(chǎn)生了貫通的滑裂帶。根據(jù)綜合關(guān)鍵點(diǎn)位移突變判據(jù)及塑性區(qū)貫通判據(jù)結(jié)果，可判定靜力工況下該邊坡的安全系數(shù)為2.4。

圖4 關(guān)鍵點(diǎn)H水平向位移與折減系數(shù)關(guān)系曲線

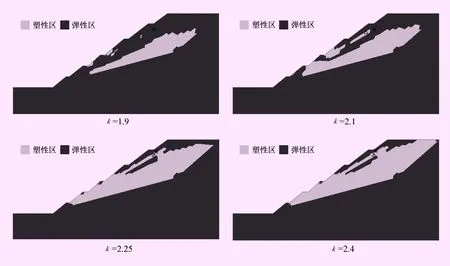
圖5 靜力工況時(shí)不同折減系數(shù)下的塑性區(qū)分布圖

2.4 動(dòng)力工況分析

地震荷載不同于靜力荷載，在地震動(dòng)持續(xù)時(shí)間內(nèi)荷載處于往復(fù)變化狀態(tài)。因此，邊坡位移隨時(shí)間會(huì)發(fā)生往復(fù)變化，僅以地震持續(xù)時(shí)間內(nèi)某一時(shí)刻的關(guān)鍵點(diǎn)位移發(fā)生突變，難以判定邊坡失穩(wěn)，但震后殘余位移發(fā)生突變?nèi)钥梢暈檫吰率Х€(wěn)的依據(jù)[10]。本文提取坡頂關(guān)鍵點(diǎn)H的震后水平向殘余位移與折減系數(shù)并繪制關(guān)系曲線，如圖6所示。

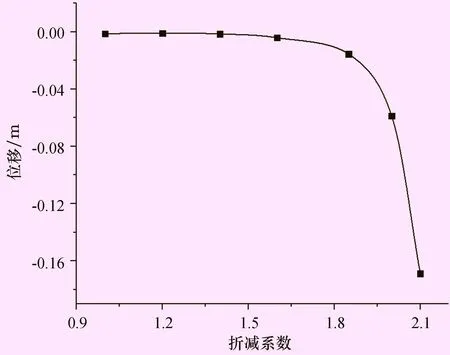
圖6 關(guān)鍵點(diǎn)H水平向位移與折減系數(shù)關(guān)系曲線

從圖6中可以看出，當(dāng)折減系數(shù)k=1～1.88時(shí)，隨著折減系數(shù)的增加，坡頂關(guān)鍵點(diǎn)H的水平向殘余位移增速緩慢；當(dāng)折減系數(shù)k>1.88時(shí)，隨著折減系數(shù)的增加，坡頂關(guān)鍵點(diǎn)H的水平向殘余位移明顯增加。從位移突變的角度，可以認(rèn)為在0.2g地震荷載作用下，當(dāng)折減系數(shù)達(dá)到1.88時(shí)，邊坡正處于臨界狀態(tài)。

圖7為動(dòng)力工況時(shí)不同折減系數(shù)下的邊坡塑性區(qū)分布圖。當(dāng)k=1.3時(shí)，塑性區(qū)主要產(chǎn)生于1號(hào)全夾強(qiáng)風(fēng)化巖和2號(hào)強(qiáng)風(fēng)化巖部分區(qū)域，隨著k的不斷增大，塑性區(qū)慢慢向四周擴(kuò)展；當(dāng)k=1.88時(shí)，塑性區(qū)延伸到坡頂，邊坡產(chǎn)生了貫通的滑裂帶。

根據(jù)關(guān)鍵點(diǎn)位移突變及塑性區(qū)貫通結(jié)果，判定0.2g地震動(dòng)作用下該邊坡的安全系數(shù)為1.88。

圖7 動(dòng)力工況時(shí)不同折減系數(shù)下的塑性區(qū)分布圖

3 結(jié) 論

(1) 該邊坡在靜力及動(dòng)力工況下的強(qiáng)度折減安全系數(shù)分別為2.4和1.88，在靜力及動(dòng)力工況下均具有較大的安全裕度。

(2) 為確保邊坡安全系數(shù)的準(zhǔn)確性，建議計(jì)算邊坡安全系數(shù)時(shí)，可綜合運(yùn)用位移突變判據(jù)和塑性區(qū)貫通判據(jù)。