懲罰函數(shù)結(jié)合遺傳算法的PID參數(shù)優(yōu)化

高興泉，黃東冬，丁三毛

(吉林化工學(xué)院 信息與控制工程學(xué)院，吉林 吉林 132022)

現(xiàn)如今，多數(shù)PID參數(shù)進行優(yōu)化的相關(guān)優(yōu)化算法在求解最優(yōu)化問題時，都是依靠適應(yīng)度函數(shù)值的大小來區(qū)分優(yōu)化結(jié)果的好壞，可以看出目標函數(shù)的選取在優(yōu)化算法中起著決定性的作用.一些常見的目標函數(shù)如絕對誤差積分[1]、誤差平方積分[2]、時間乘誤差平方積分[3]、時間乘絕對誤差積分[4]都被引用到優(yōu)化算法的過程中，這些目標函數(shù)能夠迅速減小起始誤差，并且在系統(tǒng)中反應(yīng)較快，但是系統(tǒng)中因此出現(xiàn)的超調(diào)變大將會無法避免，這些適應(yīng)度函數(shù)作用于系統(tǒng)時選擇性較差，最終導(dǎo)致系統(tǒng)的反應(yīng)速度變慢和穩(wěn)定性變差等問題.本文提出將懲罰函數(shù)[5]引入到目標函數(shù)中實現(xiàn)對PID的參數(shù)優(yōu)化的方法，首先以傳統(tǒng)遺傳算法[6]為基礎(chǔ)，選用時間乘絕對誤差積分為目標函數(shù)，然后將系統(tǒng)中出現(xiàn)的超調(diào)量作為懲罰項來構(gòu)建新的目標函數(shù).最后以雙容水箱為例的仿真結(jié)果中表明，用懲罰函數(shù)構(gòu)造出的新的目標函數(shù)能大大減小超調(diào)量，提高系統(tǒng)的動態(tài)響應(yīng)能力.

1 PID控制算法及其參數(shù)優(yōu)化

PID控制器是根據(jù)系統(tǒng)的給定值與輸出值之間的偏差作為輸入信號，利用此信號來和PID控制器中的控制算法相乘產(chǎn)生控制輸出，其控制規(guī)律如下：

(1)

其中：Kp是一個比例系數(shù)；Ki是積分系數(shù)；Kd是微分系數(shù)；e(t)是誤差信號；u(t)是PID的控制輸出.

PID控制器在實際應(yīng)用時，最為困難的在于比例、積分、微分系數(shù)的選取問題上.所以一般都會使用優(yōu)化算法對這3個參數(shù)進行優(yōu)化進而得到理想的參數(shù)來應(yīng)用于系統(tǒng).對于傳統(tǒng)優(yōu)化算法都會使用如下4種目標函數(shù)來對參數(shù)進行優(yōu)化.

對于這4種目標函數(shù)優(yōu)化出來的PID參數(shù)效果并不滿意，使得系統(tǒng)中出現(xiàn)震蕩和超調(diào)的現(xiàn)象從而導(dǎo)致系統(tǒng)不穩(wěn)定.這里提出將傳統(tǒng)目標函數(shù)中結(jié)合懲罰函數(shù)的思想來解決此類問題.

2 懲罰函數(shù)

懲罰函數(shù)法[7]的優(yōu)點是能將系統(tǒng)約束融入最優(yōu)化問題中，其中心思想就是將脫離可行域的點通過構(gòu)造懲罰函數(shù)的方式來進行約束，然后用最優(yōu)化方法解決無約束情況下的相應(yīng)的問題.然后考慮非線性約束優(yōu)化問題[8-9]：

minf(x),

(2)

s.t.gi(x)≥0,i=1,…,m,

hj(x)=0,j=1,…,l,

(3)

其中f(x)為目標函數(shù)，hj(x)(j=1,…,l)是等式約束條件，gi(x)(i=1,…,m)是不等式約束條件，三者均是在Rn上的連續(xù)函數(shù).

懲罰函數(shù)中心思想就是將問題(2)轉(zhuǎn)化為：minG(x)=f(x)+cP(x)，此處的G(x)就是懲罰函數(shù)，c為懲罰因子，P(x)則為懲罰項.

通常當(dāng)x在可行域內(nèi)時，P(x)=0，則G(x)=f(x)；當(dāng)x不在可行域內(nèi)的時候，在x處，cP(x)是很大的正數(shù)，他的存在就是迫使脫離點靠近可行域.

引理2.1[10]假設(shè)f,g,h是Rn上的連續(xù)函數(shù)，對于每一個懲罰因子c，都會存在一個xc∈Rn，使得G(c)=f(xc)+cP(xc)成立，滿足以下內(nèi)容：

(1)inf{f(x):g(x)≤0,h(x)=0}≥

supc>0G(c)，其中G(c)=inf{f(x)+cP(x)}；

(2)當(dāng)c>0時，f(x)關(guān)于x單調(diào)不降，G(c)對于c單調(diào)不降，P(xc)對于c單調(diào)不增.

為了得到滿意的過渡過程動態(tài)特性，采用時間乘絕對誤差積分為目標函數(shù):

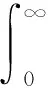
(4)

若系統(tǒng)中出現(xiàn)了超調(diào)，以原來的目標函數(shù)為基礎(chǔ)再加入懲罰函數(shù)，將系統(tǒng)中出現(xiàn)的超調(diào)量作為懲罰項加入目標函數(shù)中形成新的目標函數(shù)：

(5)

所以對于系統(tǒng)中的目標函數(shù)可以總結(jié)為:

(6)

將帶有懲罰函數(shù)的目標函數(shù)應(yīng)用到PID的參數(shù)優(yōu)化中需要一種優(yōu)化算法，這里結(jié)合傳統(tǒng)遺傳算法實現(xiàn)PID的參數(shù)優(yōu)化.

3 遺傳算法解決PID參數(shù)優(yōu)化問題

3.1 遺傳算法

遺傳算法是一種可以模擬自然界生物繁衍規(guī)則進化發(fā)展機制的隨機全局搜索和優(yōu)化學(xué)習(xí)算法.該算法的工作原理大致為以下3步：第1步，初始群體是在給定區(qū)域內(nèi)的隨機方式產(chǎn)生；第2步，通過研究選取的適應(yīng)度函數(shù)來計算各個個體的適應(yīng)度值，以適應(yīng)度值的大小來判斷所得解或個體是否為系統(tǒng)最優(yōu)；第3步，按照遺傳算子3大基本步驟進行尋優(yōu)處理，也就是選擇、交叉、變異，從而得到最優(yōu)良的個體，最終讓種群不斷地尋優(yōu)直至達到理想的目標區(qū)域內(nèi)為止.

3.2 遺傳算法求解PID參數(shù)優(yōu)化問題的步驟

遺傳算法來優(yōu)化Kp，Ki，Kd3個參數(shù)，優(yōu)化得到的參數(shù)對系統(tǒng)的控制性能有很大的改善.首先隨機產(chǎn)生初始種群，將種群信息給予PID參數(shù).若系統(tǒng)中出現(xiàn)超調(diào)，那么將超調(diào)量作為懲罰項構(gòu)造懲罰函數(shù)并且加入目標函數(shù)中，從而生成新的目標函數(shù).將新的目標函數(shù)融入遺傳算法中的性能指標中進行判斷，借助遺傳算法中的基本法則不斷優(yōu)化，直到系統(tǒng)達到最大進化代數(shù)，輸出最優(yōu)一組參數(shù).懲罰函數(shù)結(jié)合遺傳算法優(yōu)化PID參數(shù)示意圖如圖1所示.

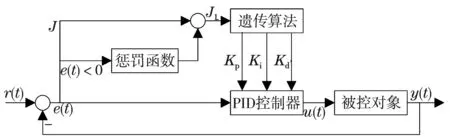
圖1 遺傳算法優(yōu)化PID參數(shù)系統(tǒng)圖

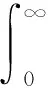
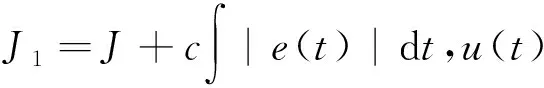
3.3 實施步驟

遺傳算法通過以下步驟優(yōu)化PID參數(shù)：

(1)按經(jīng)驗選取一組Kp、Ki、Kd參數(shù)，根據(jù)系統(tǒng)的實際情況以及要求確定約束條件，Kp∈[0,8]，Ki∈[0,2]，Kd∈[0,1].

(2)編碼及初始種群生成.采用二進制的方法對系統(tǒng)中的Kp、Ki、Kd參數(shù)進行編碼，并且設(shè)置種群規(guī)模為50，根據(jù)之前按經(jīng)驗法所得參數(shù)產(chǎn)生初始種群.

(3)系統(tǒng)如果存在超調(diào)，則選擇加入懲罰函數(shù)的目標函數(shù)J1，如果沒有超調(diào)，則選擇目標函數(shù)J作為最優(yōu)性能指標.

(4)解碼，確定適應(yīng)度函數(shù)f=1/J，根據(jù)適應(yīng)度函數(shù)來算個體適應(yīng)度值的大小來判斷并找出最優(yōu)個體.

(5)若符合優(yōu)化要求(達到設(shè)置的最大進化代數(shù))，即可輸出系統(tǒng)中最優(yōu)的一組PID參數(shù)，算法結(jié)束，若不滿足要求，按照遺傳算法的核心三大步繼續(xù)尋優(yōu)以尋得最優(yōu)一組參數(shù)為止.

(6)返回步驟(3)，若系統(tǒng)流程優(yōu)化至指定要求(達到設(shè)置的最大進化代數(shù))，將最優(yōu)解輸出，否則，繼續(xù)進行優(yōu)化.

遺傳算法優(yōu)化PID參數(shù)的流程圖如圖2所示.

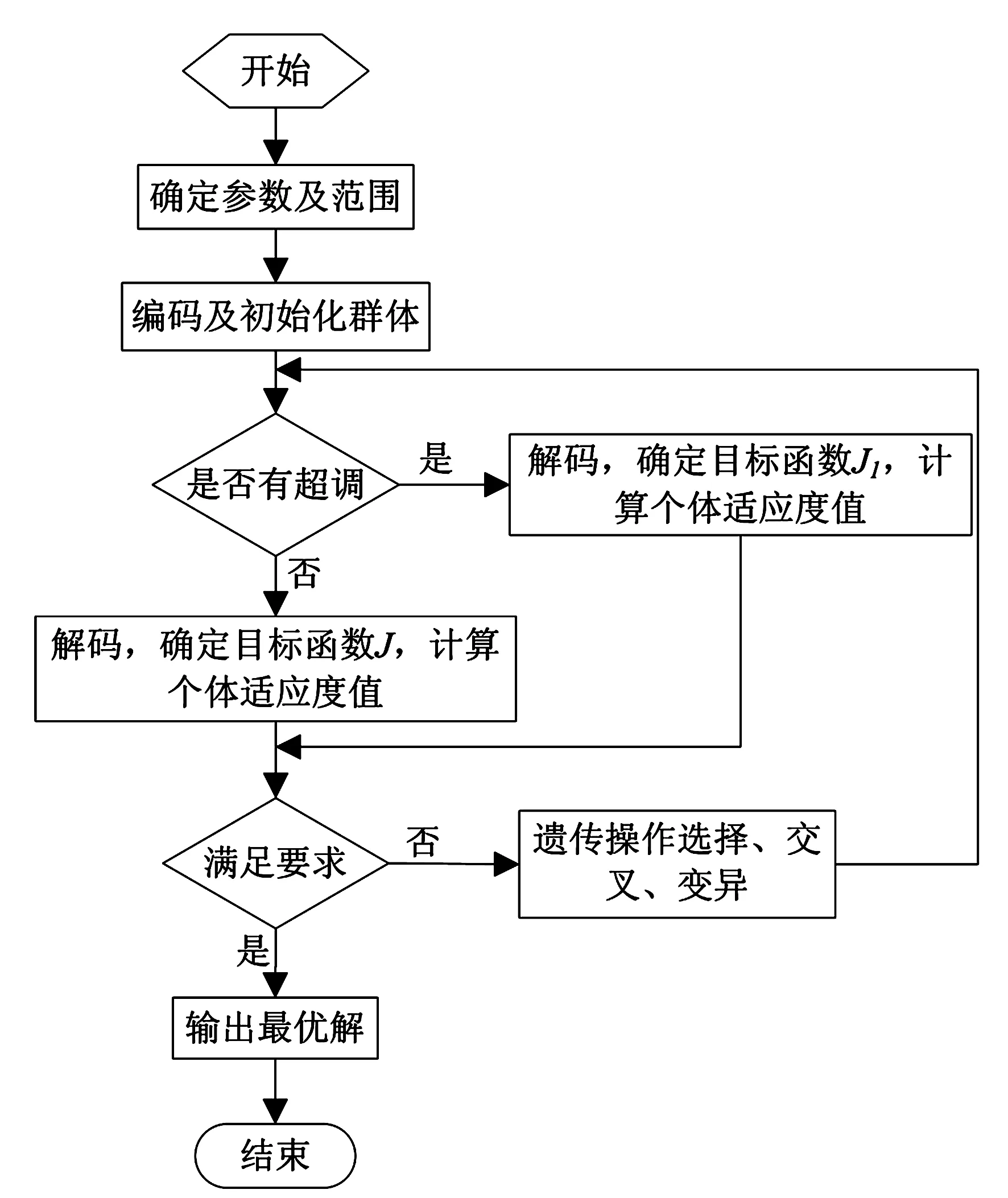
圖2 遺傳算法優(yōu)化PID參數(shù)流程

4 仿真實驗并分析

以雙容水箱系統(tǒng)為例.將懲罰函數(shù)引入到目標函數(shù)中實現(xiàn)對PID參數(shù)優(yōu)化的方法應(yīng)用到雙容水箱系統(tǒng)中.

雙容水箱模型描述如下：

(7)

其中:h1和h2分別代表上水箱和下水箱的液位；Q代表流量；其他參數(shù)代表的意義及其數(shù)值如表1所示.

表1 參數(shù)代表意義及數(shù)值

雙容水箱系統(tǒng)實際上是以下水箱的液位達到設(shè)定值為控制目標.上水箱和下水箱的初始液位均設(shè)為0.本次設(shè)計實驗是對下水箱液位達到的設(shè)定值為15 cm.

下面采用基本遺傳算法、懲罰函數(shù)引入到目標函數(shù)兩種方法對PID參數(shù)整定的仿真進行對比實驗.遺傳算法中的種群大小設(shè)置為50，進化代數(shù)為100代，交叉率為0.9，變異率為0.01，懲罰函數(shù)的懲罰因子設(shè)置為100.

兩種方法優(yōu)化PID參數(shù)結(jié)果如表2所示.

表2 兩種方法優(yōu)化PID參數(shù)的結(jié)果

圖3所示為兩種優(yōu)化PID參數(shù)方法對最優(yōu)適應(yīng)度值的對比圖.

進化代數(shù)圖3 最優(yōu)適應(yīng)度值對比圖

從圖3就可以看出，通過兩種優(yōu)化方法最后得到的最優(yōu)指標幾乎是一致的，但是基本的遺傳算法在58代的時候接近最優(yōu)，62代才能達到最優(yōu)，而懲罰函數(shù)引入到目標函數(shù)的方法在5代的時候接近最優(yōu)，到12代的時候就達到了最優(yōu)，表明了懲罰函數(shù)引入到目標函數(shù)的方法能夠大大提高系統(tǒng)的動態(tài)響應(yīng)能力.

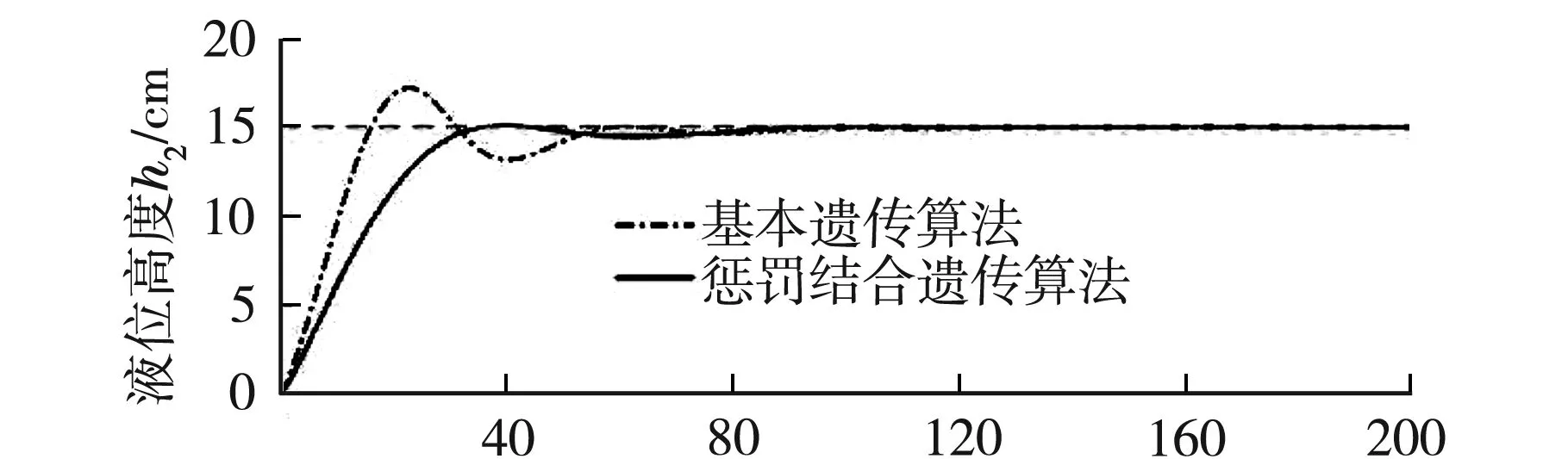
圖4為總仿真時間為200 s下的兩種優(yōu)化后的下水箱液位曲線和PID輸出控制量曲線.

從圖4可以看出，基本的遺傳算法雖然能使系統(tǒng)達到穩(wěn)態(tài)，但是系統(tǒng)中還是存在著較大的超調(diào).而用本文所設(shè)計的新目標函數(shù)的結(jié)果來看，系統(tǒng)中幾乎沒有存在超調(diào)，有效地控制了系統(tǒng)中的超調(diào)量，并且能夠有效地改善系統(tǒng)控制性能的穩(wěn)定性.

t/s

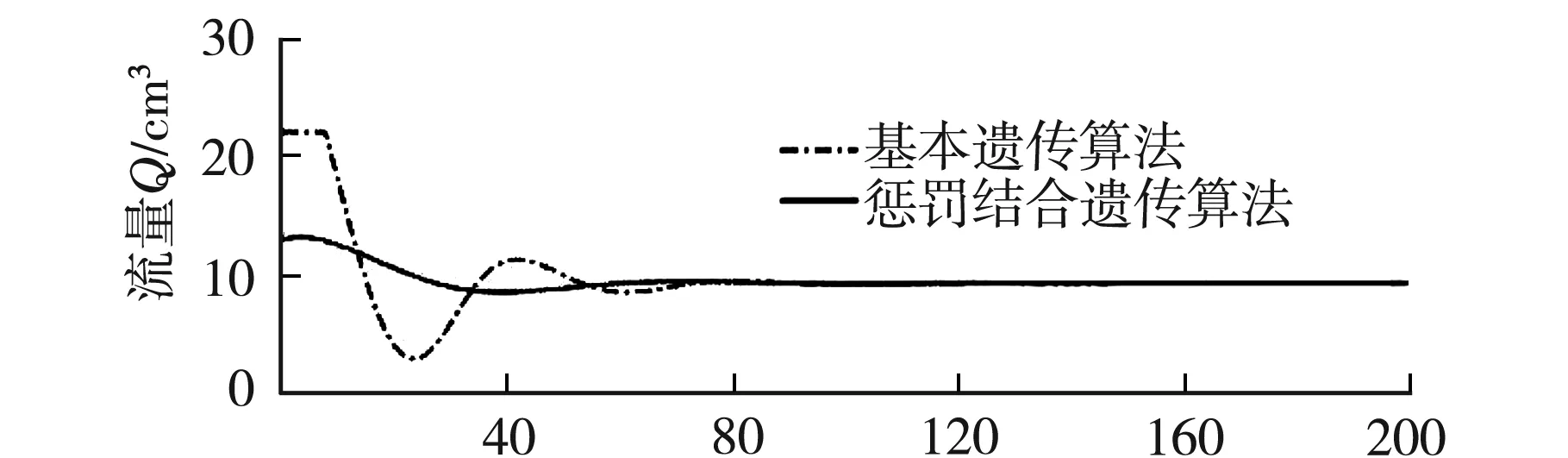
t/s圖4 液位曲線及控制量曲線

5 結(jié) 論

針對傳統(tǒng)優(yōu)化算法對PID參數(shù)優(yōu)化時，由于目標函數(shù)選擇不當(dāng)出現(xiàn)的超調(diào)量過大，從而引起系統(tǒng)的反應(yīng)速度變慢和穩(wěn)定性變差的問題，提出了懲罰函數(shù)引入到目標函數(shù)中實現(xiàn)對PID的參數(shù)優(yōu)化的方法.在系統(tǒng)的運行過程中，一旦產(chǎn)生超調(diào)，則懲罰函數(shù)將會用超調(diào)量作為懲罰項加入目標函數(shù)中，進而形成新的目標函數(shù)，遺傳算法將會以帶有罰函數(shù)的目標函數(shù)進行優(yōu)化.本文中，以雙容水箱系統(tǒng)仿真為例，實踐仿真結(jié)果表明，懲罰函數(shù)引入到目標函數(shù)中實現(xiàn)對PID的參數(shù)優(yōu)化的方法能有效地減小了超調(diào)量，加快優(yōu)化以及運行速度的同時保證了系統(tǒng)的穩(wěn)定性.