ON THE MIXED RADIAL-ANGULAR INTEGRABILITY OF MARCINKIEWICZ INTEGRALS WITH ROUGH KERNELS?
Ronghui LIU(劉榮輝) Feng LIU(劉鳳) Huoxiong WU(伍火熊),?
1.School of Mathematical Sciences,Xiamen University,Xiamen 361005,China
2.College of Mathematics and System Science,Shandong University of Science and Technology,Qingdao 266590,China E-mail:liuronghuimath@126.com;FLiu@sdust.edu.cn;huoxwu@xmu.edu.cn
Abstract This paper studies the mixed radial-angular integrability of parametric Marcinkiewicz integrals along“polynomial curves”.Under the assumption that the kernels satisfy certain rather weak size conditions on the unit sphere with radial roughness,the authors prove that such operators are bounded on the mixed radial-angular spaces.Meanwhile,corresponding vector-valued versions are also obtained.
Key words Marcinkiewicz integrals;rough kernels;mixed radial-angular spaces
1 Introduction
Let Sbe the unit sphere in R,n≥2,with normalized Lebesgue measure dσ=dσ(·).For any f∈L(R),0 Therefore,from the perspective of radial and angular integrability,Lebesgue norms can be interpreted as certain special norms with the same integrability in the radial and angular directions.Inspired by this version of things,we naturally consider the case of Lebesgue norms with different integrability in the radial and angular directions,namely, It is worth pointing out that the spaces G(S)were introduced by Grafakos and Stefanov[14]in studying the L-boundedness of singular integrals with rough kernels,and it was shown in [14]that On the other hand,as a special case of the Littlewood-Paley-Stein functons,Marcinkiewicz integrals play important roles in harmonic analysis.We refer the readers to [1,2,5,8,9,16,19,23,26–29]etc.for their development and applications.In this paper,we will focus on the following parametric Marcinkiewicz integrals along polynomial curves: where P(t) is a real polynomial on R of degree N satisfying P(0)=0,? enjoys (1.2) and ρ is for a complex number with ρ=τ +i?(τ,? ∈R,τ >0),h ∈△(R) for 1 ≤γ ≤∞,where△(R) is the set of all measurable functions h defined on Rsatisfying In light of the aforementioned facts concerning the Marcinkiewicz integral operators,two questions that arise naturally are: In this paper,we shall give affirmative answers to the above questions.Our results can be formulated as follows: Theorem 1.1 Theorem 1.2 Corollary 1.3 Remark 1.4 for 2 ≤p<2β/s,provided that ? ∈G(S) for any s>β,or for β 2.These results partly recover the corresponding results in [5]. The rest of this paper is organized as follows:in Section 2,we will establish a key lemma,which contains a general criterion on the weighted inequality of the convolution operators.By virtue of the general criterion,we only need to check the corresponding conditions to derive the weighted inequality of Marcinkiewicz integrals.Therefore,the boundedness of the parametric Marcinkiewicz integral operators on the mixed radial-angular spaces,vector-valued mixed radial-angular spaces will automatically hold by [20,Proposition 1].The proofs of theorems will be given in Section 3.Finally,as applications of our main results,we obtain the mixed radial-angular integrability for the corresponding parametric Marcinkiewicz integral operators related to the area integrals and the Littlewood-Paley gfunction in Section 4.We would like to remark that some ideas in the proofs of our main results are taken from [10,14,15,18,21]. In this section,we will establish a general criterion on the weighted boundedness of the convolution operators,which is a key to our proofs.On the basis of the general criterion,then,a key proposition related to Marcinkiewicz integral operators is also obtained accordingly. By means of Lemma 2.1 we can prove the following weighted norm inequality on Marcinkiewicz integral operators,which plays a significant role in the proof of Theorem 1.2: Proposition 2.2 To obtain the proofs of our theorems,we also need the following criterion about the boundedness of the operators on the mixed radial-angular spaces: for all s>sand any nonnegative measurable function u on R,where the operator Mmaps any radial function to radial function,and satisfies This section is devoted to the proofs of our main theorems.In fact,we only prove Theorem 1.2 because the conclusions of Theorems 1.1 can be similarly obtained by a slight modification.More precisely,suppose that ? ∈G(S) for some β >1,h ≡1 and make the following substitution in Theorem 1.2 :β →2β,this reduces it to Theorem 1.1.Therefore,we focus on the proof of Theorem 1.2. First,we consider the condition (i).By (2.19),we have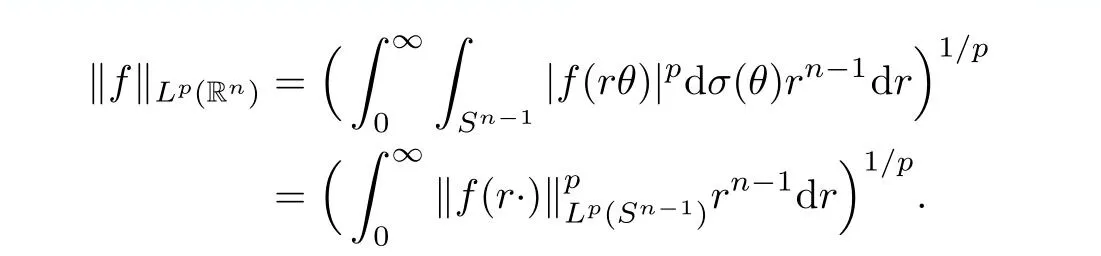
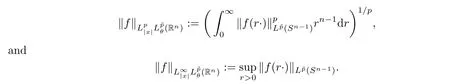

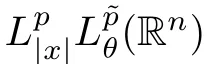
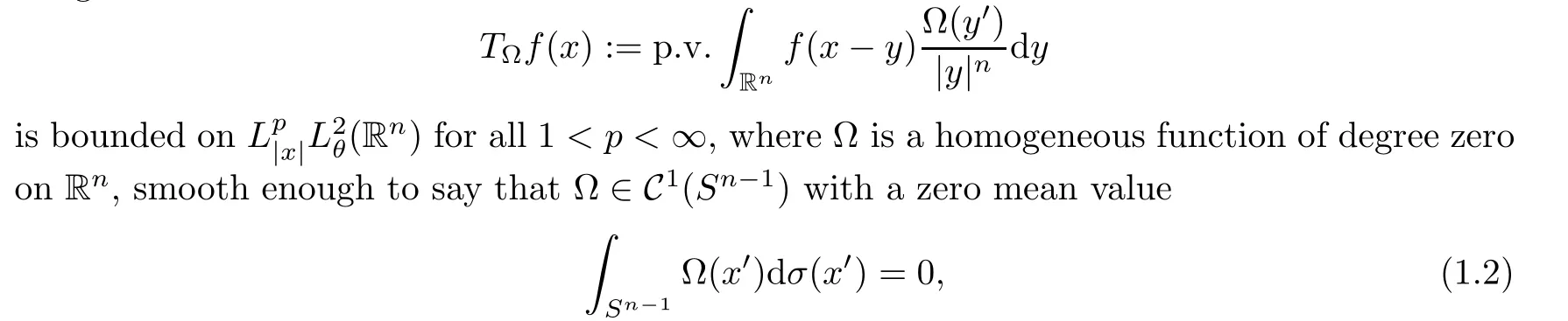
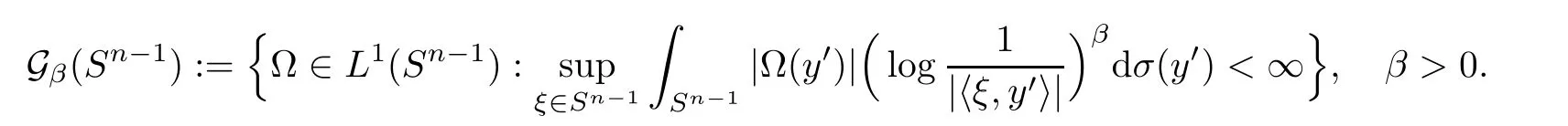
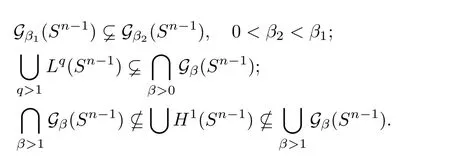


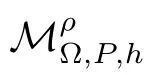
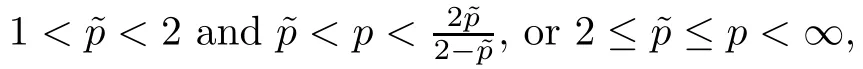
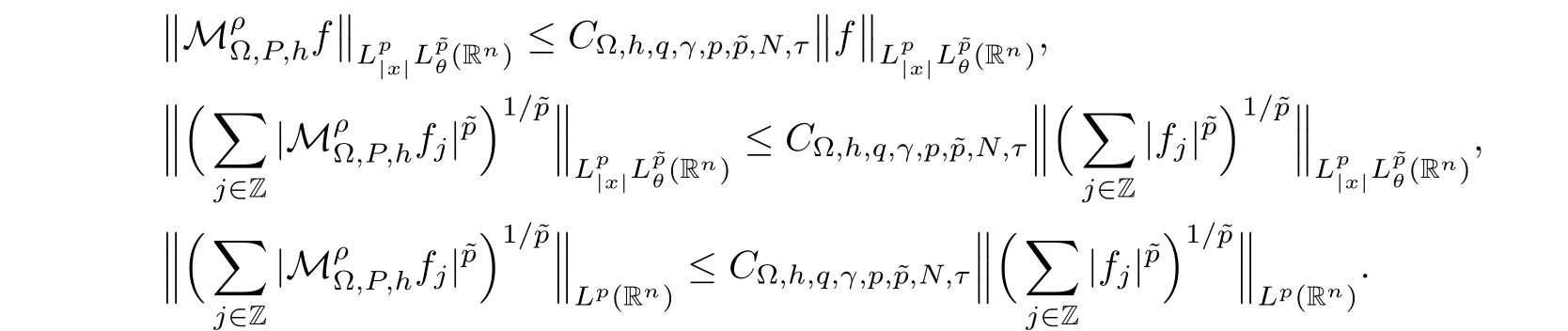
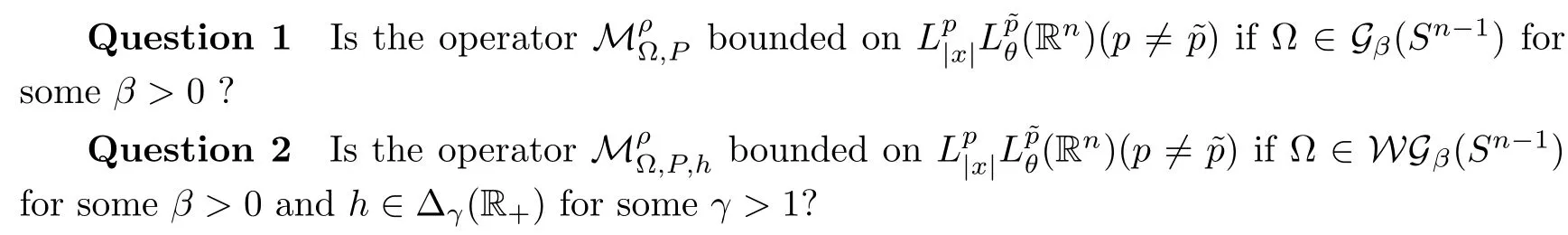


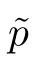


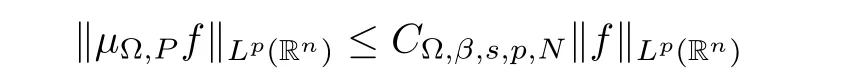
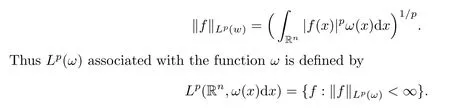
2 Main Lemma and Key Proposition

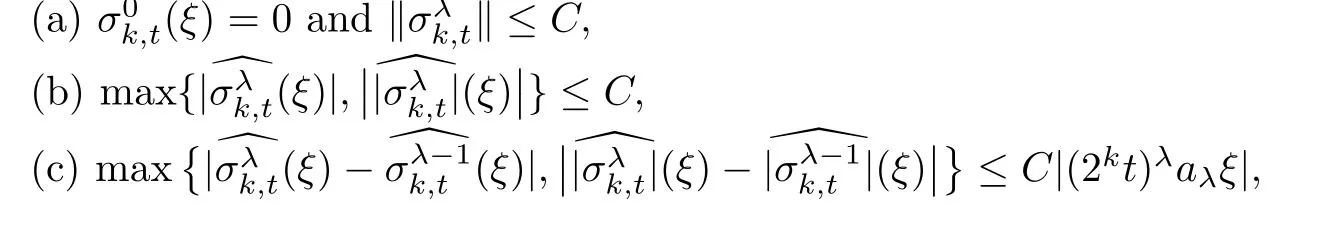


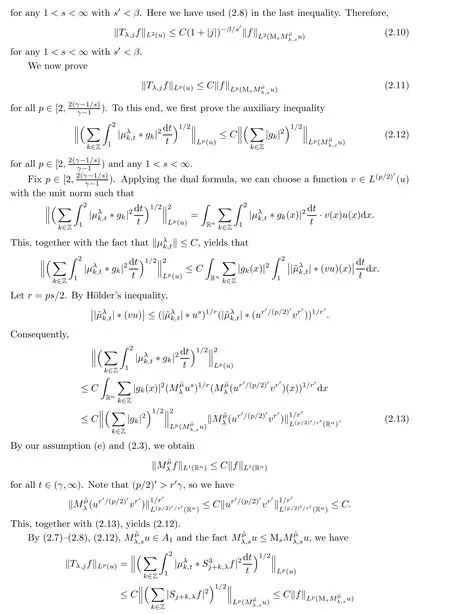


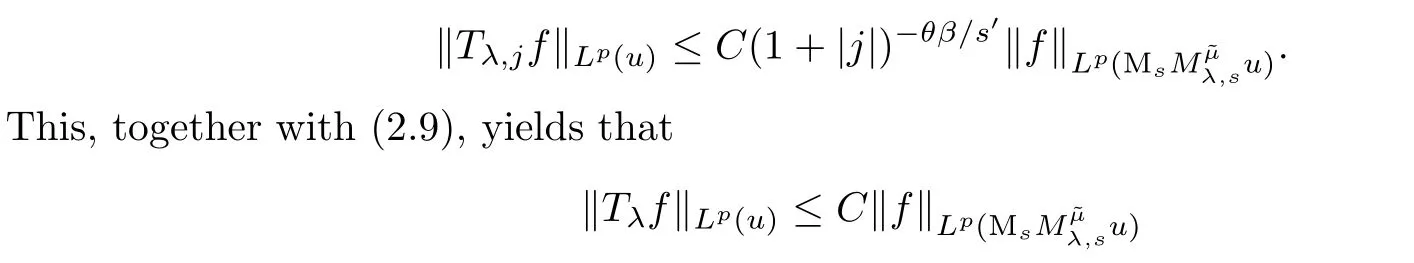
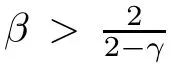




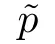
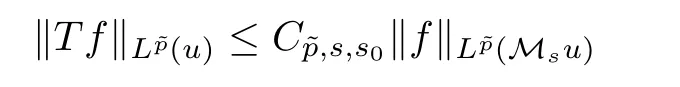
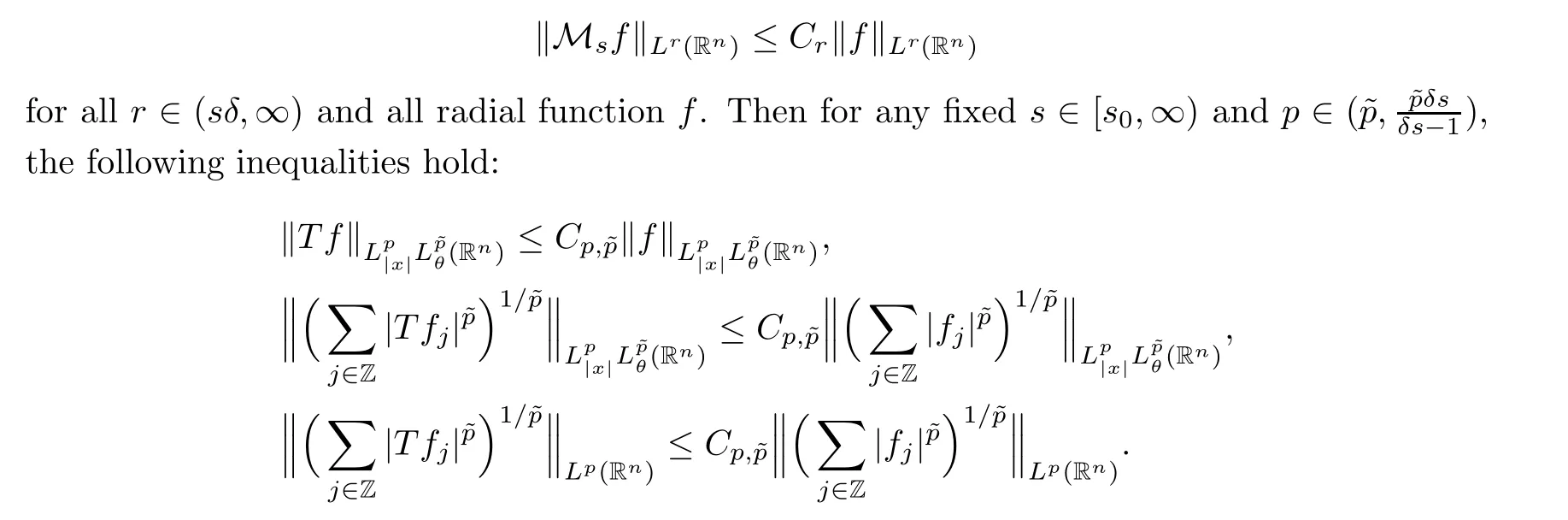
3 Proofs of Theorems
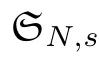

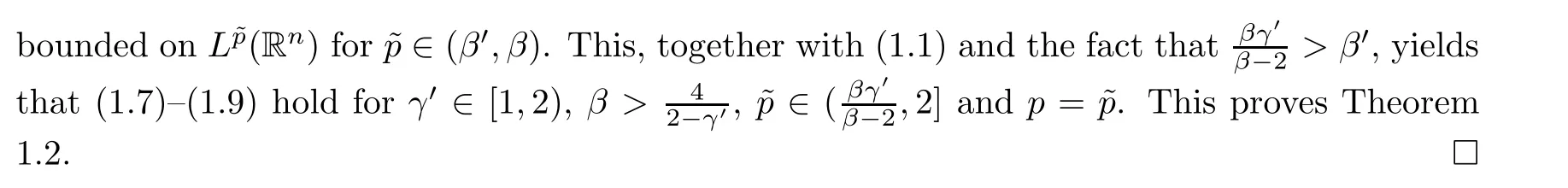
4 Additional Results


 Acta Mathematica Scientia(English Series)2021年1期
Acta Mathematica Scientia(English Series)2021年1期
- Acta Mathematica Scientia(English Series)的其它文章
- THE LOCAL WELL-POSEDNESS OF A CHEMOTAXIS-SHALLOW WATER SYSTEM WITH VACUUM?
- UNDERSTANDING SCHUBERT’S BOOK(I)?
- GLEASON’S PROBLEM ON FOCK-SOBOLEV SPACES?
- THE EXISTENCE AND STABILITY OF STATIONARY SOLUTIONS OF THE INFLOW PROBLEM FOR FULL COMPRESSIBLE NAVIER-STOKES-POISSON SYSTEM?
- ON THE CAUCHY PROBLEM FOR AW-RASCLE SYSTEM WITH LINEAR DAMPING?
- DOOB’S MAXIMAL INEQUALITIES FOR MARTINGALES IN VARIABLE LEBESGUE SPACE?
