基于AHP 的區域干旱等級綜合評價及其應用

蔣 欣，常留紅，楊思宇，王瀚銳，周 磊

（1.湖南省鑫譽項目管理有限責任公司，湖南 長沙 410000； 2.長沙理工大學水利工程學院，湖南 長沙410114； 3. 湖南省水利水電科學研究院，湖南 長沙 410007）

前 言

干旱作為最嚴重的氣象災害之一，影響范圍廣，持續時間長，后續和潛在損害大，已經對我國社會經濟和人民生活造成嚴重影響。受全球氣候變化和經濟社會高速發展的影響，干旱呈現頻次增加、范圍擴大之勢。目前，我國60%以上的縣區為易旱地區，旱情重、影響程度深，治理點多面廣，抗旱減災任務艱巨繁重，所需資金較大，因此，必須按照輕重緩急、突出重點、效率優先的原則，進行分級治理。

國內外許多學者從氣象干旱、農業干旱、水文干旱、社會經濟干旱四個方面對干旱及干旱指標評定做了大量研究[1～2]。Palmer[3]提出了帕爾默干旱指標（PDSI），有效地反映了地區干旱程度及干旱時間尺度；Bhalme[4]提出區域旱澇指數（DAI/FAI），該指數有效說明了區域和年季尺度的水分狀況。Palmer[5]在PSDI 指標的基礎上，提出了應用于較大空間尺度上的作物水分指標（CMI），能夠充分反應短期農作物的水分狀況；孫榮強[6]通過水平衡干旱模擬模型，確定了綜合考慮氣候-土壤-植物體系和各時段旱象對整個作物旱情的影響程度的旱情評價體系；邱林[7]建立能準確反映干旱對農業造成損失的農業干旱評估指標的靜態模型和動態模型。熊立華、任立良[8～10]引進了具有物理分布機制的分布式模型和水文干旱模型。Ohlsson[11]提出了概化干旱對社會影響的SWSI 指標。馮平[12]采用人工神經網絡技術的方法，提出干旱程度的評估模型。馮利華[13]根據風級和震級的計算原理，提出了干旱等級和災度的概念。

隨著人類活動的不斷加劇，區域干旱也表現出差異性、隨機性、突發性、重現性以及無序性等復雜性的特點，加之干旱對社會影響的廣泛性及自身的時空局限性，因此，單一的干旱評價指標難以有效反應干旱的內在機理及其影響程度，本文基于層次分析法，建立干旱影響指標體系，建立區域干旱等級綜合評價模型，結合現行的分項旱災評價標準，提出干旱等級綜合評價標準。根據衡邵干旱走廊33 個縣（市、區）1990-2010年的統計數據，將評價模型應用于33 個縣（市、區），通過干旱等級分級，并對該區域內33 縣（市、區）實施分級治理，為區域干旱分級綜合治理提供科學依據。

1 AHP 評價原理

1）建立指標體系

干旱評價指標涉及領域較多，相互關系復雜，在選取綜合評價指標時應遵從科學性、系統性、可比性、動態性和簡明性原則，選取指標體系應具有明確的內涵，盡可能全面地反映干旱的特征，并考慮指標的可測性、規范性、一致性和實用性，盡可能具有較長期的數據資料，可進行不同時期比較研究。

2）判斷矩陣

對從屬于上一層某要素Ai的同層各個要素Bi進行兩兩比較，以要素Ai作為判斷準則進行量化標度比較，構成判斷矩陣B[B=（bij）n×n]。

判斷矩陣中各個元素的數值一般采用1～9 位標度法確定，在相鄰的2 個等級之間可依次用2、4、6、8 或其倒數將其量化，如表1 所示。

表1 判斷矩陣取值

3）計算權向量

根據判斷矩陣B 求出其最大特征特征值λmax和對應的特征向量W，特征向量W 經歸一化后即為所求權向量，計算判斷矩陣中與上一層某一因素有關的同一層次因素之間相對重要性的次序權值。

4）一致性檢驗

在實際應用中為避免其他因素對判斷矩陣的干擾和保證判斷矩陣滿足大體一致性，需要進行一致性檢驗，符合一致性要求。判斷矩陣一致性檢驗計算：

其中，CR 是一致性判斷指標，當CR＜0.1 時，判斷矩陣符合一致性要求，否則需要對判斷矩陣進行調整；CI 是判斷矩陣的一致性指標：

其中，λmax是判斷矩陣的最大特征值，n 是成對因子比較的個數。

RI 為隨機一致性指標，通過查表確定，如表2所示。

表2 隨機一致性指標RI 值

2 區域干旱等級綜合評價模型

2.1 評價指標體系

干旱評價指標涉及領域較多，相互關系復雜，本文結合各地區水資源條件、水利基礎設施供水能力和經濟社會發展實際需求的基礎上，緊扣水資源與“三生”用水的主要矛盾及存在的突出問題，根據相關干旱等級評價標準，統籌各地區干旱特征，選取受災人口百分比（受旱人口占總人口的百分比）、農作物受災面積百分比（農業受旱面積占總耕地的百分比），缺水率（缺水量占總需水量）、經濟損失百分比（受旱影響經濟值占區域GDP 的百分比）、石漠化程度（石漠化面積占國土面積的比例）等5 項綜合指標，建立區域旱情評價指標體系。區域干旱等級綜合評價遞階層次模型，如圖1 所示。

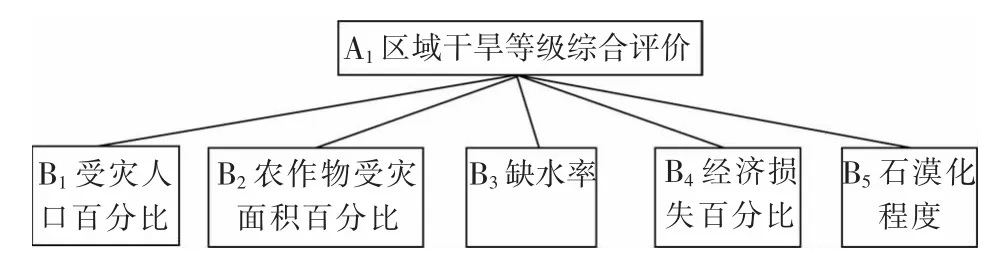
圖1 區域干旱等級綜合評價遞階層次模型

2.2 計算各項評價指標權重值

基于Dephi 專家調查法和1～9 位標度法，對同屬于上一層某因素（A1）的同層各個因素（Bi）進行兩兩比較，并對其相對重要性賦予一定分值，從而構造出上下層次之間隸屬關系的判斷矩陣B[B=（bij）5×5]，如表1 所示，計算權向量W 采用和積法；判斷矩陣見表3。

表3 判斷矩陣A-B 數值表

對矩陣B 的每一列進行正規化，

計算出正規化后的矩陣B 為：

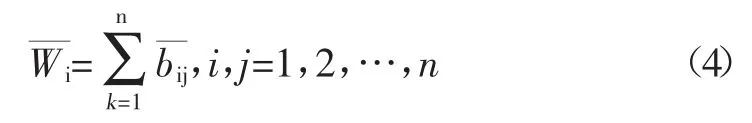
和積法中計算判斷矩陣B 最大特征值λmax公式如下，

其中

由表2 可知隨機一致性指標RI=1.12，根據式（1）、式（2）進行判斷矩陣的一致性檢驗，得：CI=0.017 5，CR=0.015 6<0.1，判斷矩陣符合一致性要求。見表4。

表4 區域干旱等級綜合評價模型

3 衡邵干旱走廊干旱等級計算

基于衡邵干旱走廊1990—2010 年20 年的統計數據，將區域干旱等級綜合評價模型應用于衡邵干旱走廊33 個縣，對各縣區的干旱情勢進行綜合評價。

干旱指數=人口百分比×0.42+農作物受旱面積百分比×0.26+缺水率×0.16+經濟受旱百分比×0.10+石漠化程度百分比×0.06；干旱綜合評價指數=某縣區干旱指數/所有縣區干旱指數之和；以衡陽縣干旱綜合評價指數計算為例，衡陽縣干旱指數=11.61%×0.42+18.75%×0.26+6.57%×0.16+3.6%×0.10+2.74%×0.06=0.113。

衡陽縣干旱綜合評價指數=0.113/4.0921=0.0276。

同理，計算其他縣（市、區）干旱綜合評價指數計算結果，見表5。

表5 衡邵干旱走廊干旱綜合評價指數

根據《氣象干旱等級》、《農業干旱等級》和《干旱災害等級》國家標準，確定規劃區干旱綜合等級劃分標準，將規劃區分為嚴重干旱區、重度干旱區、中度干旱區和一般干旱區四個等級，見表6 和表7。

表6 衡邵干旱走廊綜合治理等級標準

表7 衡邵干旱走廊綜合治理等級區劃表

4 結 語

1）基于層次分析法，在充分考慮干旱對社會影響的廣泛性及自身的時空局限性的基礎之上，建立了區域干旱等級綜合評價模型，有效反應干旱的內在機理及其影響程度，并結合《氣象干旱等級》、《農業干旱等級》和《干旱災害等級》，提出干旱等級綜合評價標準，對區域干旱進行干旱等級區劃，實施分級治理，為區域干旱綜合治理提供科學依據。

2）應用區域干旱等級綜合評價模型及標準，對衡邵干旱走廊進行干旱綜合等級評定，將衡邵干旱走廊的各縣（市區）根據等級標準分級，為實施分級治理，有效降低特大干旱對區域的社會經濟影響提供借鑒作用。本模型適用于在干旱治理點多面廣、抗旱減災任務艱巨繁重、所需資金較大的干旱區域推廣應用。