基于RBF神經網絡優化的無人駕駛車輛增量線性模型預測軌跡跟蹤控制研究

肖宗鑫，李曉杰，肖宗爍，張志文，董小瑞

（1.中北大學 能源動力工程學院，太原 030051；2.東北林業大學 經濟管理學院，哈爾濱 150040）

由于在提升車輛主動安全性、改善交通效率以及降低能耗等方面的巨大潛能，無人駕駛技術已經成為當前車輛行業的研究熱點［1-2］，而軌跡跟蹤是無人駕駛車輛的研究重點之一［3］。

模型預測控制（MPC）［4-5］具有很高的控制精度，且便于添加約束條件，在過程控制中被廣泛應用［6］。Borrelli等［7］、Falcone等［8-9］設 計了MPC控制器，實現了車輛前輪的自動轉向，較好地完成了軌跡跟蹤任務；ATTIA等［10］基于非線性模型預測控制設計了側向控制器，計算負擔大，不適于高速工況；對于線性模型預測控制，李培新等［11］只考慮了運動學因素的影響，王秋等［12］僅建立了2自由度的車輛動力學預測模型，孫銀健［13］研究了車輛在低附著路面的軌跡跟蹤問題，將最高安全速度限定在12 m／s內；線性時變模型預測控制實時計算量相對較小，但當狀態偏離線性化工作點時可能會產生較大的預測誤差從而導致系統不穩定［14］；鄒凱等［15］考慮輪胎力進入非線性區［16］的情況，設計了增量線性MPC（ILTV-MPC）提高了計算的實時性。

HU Jianjun等［17］提出利用模糊控制對ILTVMPC補償控制，但模糊控制器不具備自適應能力，無法滿足復雜的行駛工況，且缺乏理論上的穩定性證明；引入包絡線約束的ILTV-MPC優化方法［18-19］和變步長的模型離散化方法［20-22］僅集中于對轉向的優化；BROWN M等［23］提出了N-MPC并進行了實車驗證，但可能陷入局部最優。

傳統MPC對系統不確定性的處理能力有限，當系統模型描述不準確或者存在外部擾動時，往往難以實現既定的控制目標［24］。神經網絡具有并行運算能力強、學習和容錯能力強等優點，研究基于神經網絡的自適應軌跡跟蹤算法具有重要的實際意義，其中RBF（徑向基函數）網絡是連續函數的最佳逼近［25］。同時，為了滿足不確定性系統的控制需求，魯棒模型預測控制是未來的發展方向［26］。

本研究在ILTV-MPC基礎上，利用RBF的局部逼近特性，設計了RBF自適應補償控制器對MPC模型的不精確部分進行逼近；但由于在逼近過程中仍會存在誤差，進而將RBF神經網絡與魯棒控制相結合，設計了RBF魯棒優化控制器，將逼近誤差作為外部干擾予以抑制；應用Lyapunov函數推導了隱含層網絡權值訓練規則，并證明了2個控制系統的穩定性。最后，搭建Simulink／Carsim聯合仿真平臺對3種軌跡跟蹤控制系統進行對比仿真驗證。

1 ILTV-MPC軌跡跟蹤控制器

1.1 預測模型

采用3自由度車輛-輪胎模型進行動力學分析，為簡化計算，在較為準確地描述車輛動力學過程的基礎上，進行如下假設：①假設無人駕駛車輛只做前輪轉向；② 忽略車輛垂向運動、縱向和橫向空氣動力學的影響；③忽略懸架運動及其對耦合關系的影響；④用非線性單軌模型描述車輛運動，不考慮載荷左右轉移。

利用Pacejka提出的魔術公式（magic formula，MF）對每個控制周期進行線性化處理，計算出適用范圍更大的輪胎縱向力、側向力和回正力矩等輸出變量，得到輪胎時變模型，進而結合車輛3自由度單軌模型［4］。

得到基于上述假設的3自由度車輛非線性動力學模型：

式中：a、b分別為質心到前、后軸的距離；m為車輛整備質量；Iz為車輛繞z軸的轉動慣量；δf為前輪轉角；φ為質心橫擺角；Cl為輪胎縱向側偏剛度；Cc為輪胎橫向側偏剛度。

由車身坐標系和慣性坐標系之間的轉換關系，可得：

將車輛的動力學模型近似線性化，在任意點（ξt，ut）處進行泰勒展開并只保留1階項，忽略高階項，則可得到：

對式（4）進行近似離散化處理，同時結合系統的狀態量和狀態量參考值之間的偏差，表示為：

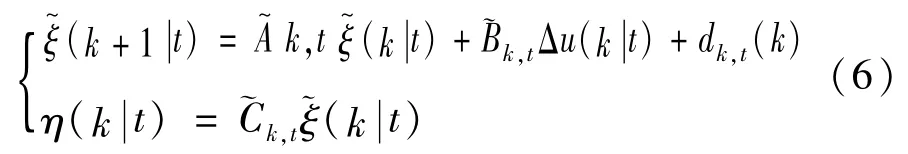
式中各狀態系數矩陣、控制系數矩陣和輸出系數矩陣為：

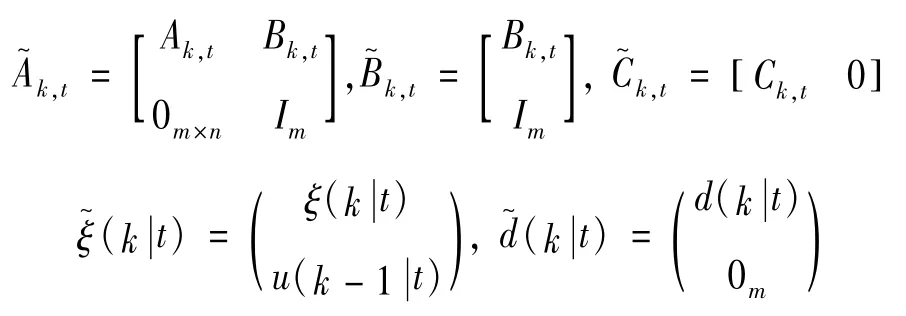
設定系統的預測時域為Np，控制時域為Nc，從而實現模型預測控制算法的預測功能。

1.2 優化求解

車輛動力學模型雖已經過一定程度的簡化，但仍有較大的計算復雜度，而且系統的模型是實時變化的，可能會出現規定時間內無法得到最優解的情況，所以引入松弛因子，使每次優化都能得到可行解。由文獻［4］優化目標函數設為以下形式：

式中：ρ表示權重系數；ε表示松弛因子；Q表示輸出偏差的權值矩陣，R表示控制增量的權重系數。

為保證車輛能夠平穩地跟蹤期望軌跡，設計了前輪轉角及其增量約束、質心側偏角約束、加速度約束和輪胎側偏角約束，其中為防止求解失敗，在加速度約束中引入松弛因子，設為軟約束。

將ILTV-MPC每一步帶約束的目標函數優化求解問題轉換為如下二次規劃問題以方便計算機求解：

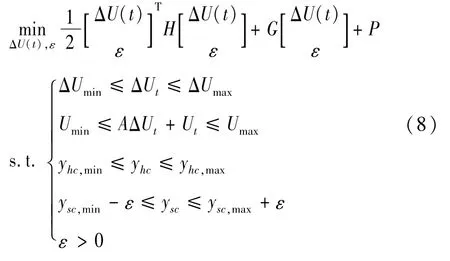
式中：yhc為硬約束輸出；ysc為軟約束輸出；yhc，min和yhc，max為硬約束輸出極限值；ysc，min和ysc，max為軟約束輸出極限值。

1.3 反饋校正

在每個控制周期內完成對式（8）的求解后，可以得到控制時域內一系列控制輸入增量：

將得到的控制序列中的第1個元素作為實際輸入增量，可得到未來時刻的輸入量：

Δut作用于系統的當前時刻，系統執行這一控制量直到下一時刻，在新的時刻，系統根據狀態信息重新預測下一段時域的輸出，再次求解優化目標函數，可得到一個新的控制增量序列，再將其作用于系統的下下個時刻，循環往復，形成最優滾動控制［4］。

如此，完成了增量線性時變模型預測軌跡跟蹤控制器的建立。

2 RBF神經網絡自適應補償控制器

由于在建立ILTV-MPC預測模型過程中進行了諸多假設和簡化，這些假設和簡化的存在必然會導致控制器模型存在一定的不精確部分f，進而導致軌跡跟蹤誤差的增大，因此，設計了RBF自適應補償控制器對不精確部分進行逼近。

2.1 ILTV-MPC控制器建模不精確部分

將建立的車輛動力學模型式（1）以狀態方程的形式表示：

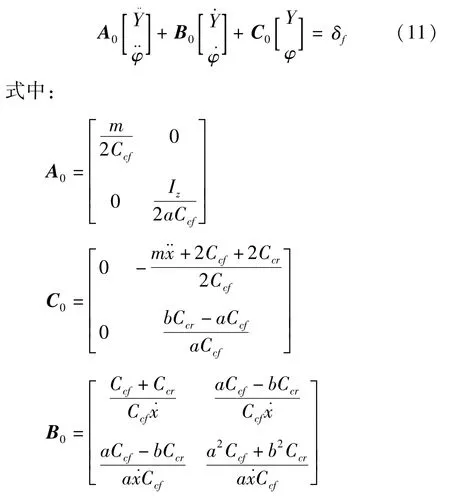
令q＝[Y ]φT，則可將式（11）寫為

式中：A0、B0和C0在實車模型中為未知參數，但在本節設計的車輛動力學模型中若暫時忽略建模過程中的假設和簡化，可認為其是已知量，即式（12）所示的車輛動力學模型是精確的，則控制律暫可設計為：

將式（13）代入式（12），可得：

此時可認為系統是閉環穩定的，但由于真實的車輛模型很難得到，故假設實際的車輛模型為：

將式（13）代入實際的車輛模型式（15），可得到

式中：ΔA＝A-A0、ΔB＝B-B0、ΔC＝C-C0。結合式（14）（16）可取ILTV-MPC控制器中由于建模過程的假設和簡化而產生的不精確部分為f＝

因此，控制律（13）可修正為

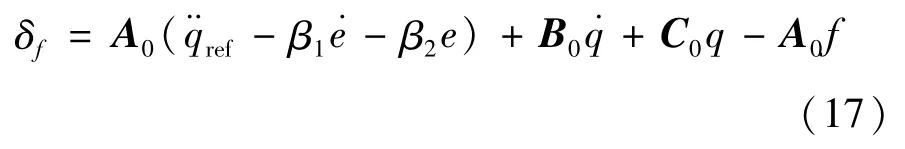
2.2 RBF自適應補償

本文建立的RBF神經網絡結構為2-5-1，輸入向量為橫向位置和橫擺角誤差e及其誤差變化率隱含層以高斯函數作為核函數；輸出向量為模型的不精確部分。

隱含層高斯基函數按下式計算：

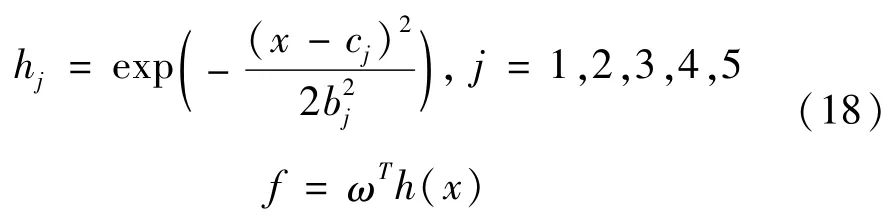
式中：x為網絡的輸入；cj為第j個節點的中心值向量；bj為第j個節點的高斯基函數基寬值；h（x）＝［h1h2h3h4h5］T為高斯基函數的輸出；ω為神經網絡權值。

假設x＝（e˙e）T，可得到在控制律（17）下的誤差狀態方程：

由文獻［23］可知，RBF神經網絡的建模誤差η是有界的，假設其上界為 ηsup，即 ηsup＝

因此，RBF神經網絡輸出的估計值為：

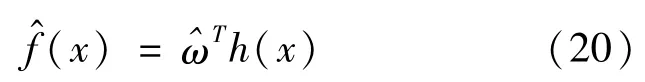
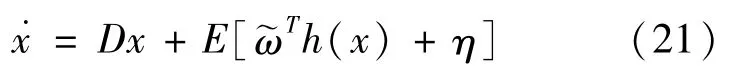
由此可得到車輛動力學模型前輪轉角：

2.3 Lyapunov穩定性分析

針對本節控制系統，采用Lyapunov穩定性分析的方法對雙移線期望軌跡的數據進行網絡權值訓練。

定義Lyapunov函數為：

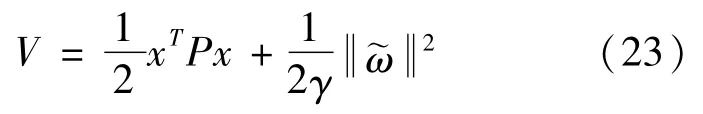
式中：γ為待定系數，本節γ取20；P為對稱正定矩陣，且滿足Lyapunov方程：

對V求導并代入式（21）（25）得到：

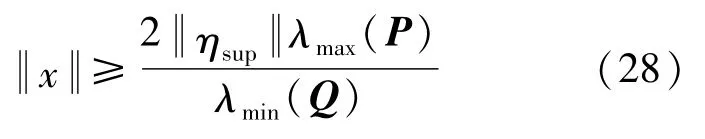
由式（28）可知，Q的特征值越大，P的特征值越小；建模誤差上界ηsup越小時，x的收斂半徑越小，所建立的控制器補償能力越好，軌跡跟蹤效果越好。因此，本節設計的控制系統是穩定的。

由此，完成了RBF神經網絡對ILTV-MPC軌跡跟蹤控制器不精確部分的補償控制。

3 RBF神經網絡魯棒控制器

由于RBF神經網絡逼近過程中仍會存在一定的逼近誤差，因此將RBF神經網絡和魯棒控制相結合，利用魯棒抑制外界干擾的特性，將逼近誤差作為外部干擾，設計了RBF魯棒優化控制器，對其予以抑制。

仍采取所設計的2-5-1結構的RBF神經網絡，但定義輸入向量為：

式中，α為待定系數，經多次仿真實驗測試，α值取0.3。

3.1 RBF神經網絡魯棒控制

當考慮模型不精確部分和外部干擾時，式（12）可修正為：

式中：f為模型的不精確部分；d為外部干擾。

通過采用前饋項進行非線性補償，取控制律為：

ε表示RBF神經網絡的逼近誤差，結合式（30）和（31），可得到系統的狀態誤差方程：

結合式（32），式（29）可轉化為：

控制器u控制律設計為：

系統的L2增益可體現控制系統對外界干擾的抑制能力，控制系統的干擾抑制問題可歸結為設計控制器使L2增益盡可能小或者小于給定值γ，γ＞0［27］。

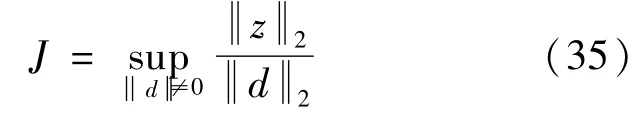
對于上述閉環控制系統，設定評價信號z＝pe＝px1，若其中的參數p滿足：

式中：ε0為給定常數，則該閉環系統的L2增益小于給定值 γ，γ值取0.1。

3.2 Lyapunov穩定性分析

針對建立的閉環控制系統，定義Lyapunov函數為：

對V求導，同時代入式（34）（35），可得：

取自適應律為：

結合式（38）（39）可知

根據L的定義，可知

由HJI（Hamilton Jacobi Issacs）不等式定理可知，此時控制系統L2增益小于γ，性能指標滿足J≤γ，即本節設計的閉環控制系統是穩定的。

綜上所述，完成了RBF魯棒優化控制器對RBF補償控制的改善，即完成了對ILTV-MPC軌跡跟蹤控制器的再次優化。

4 仿真與分析

針對所設計的RBF補償-ILTV-MPC和RBF魯棒-ILTV-MPC兩種控制系統，無人駕駛車輛的輸入前輪轉角δf由ILTV-MPC軌跡跟蹤控制器輸出δf0和RBF補償控制器或者RBF魯棒控制器輸出δf1共同組成。

系統控制框圖如圖1、2所示。

圖1 RBF補償-ILTV-MPC系統控制框圖

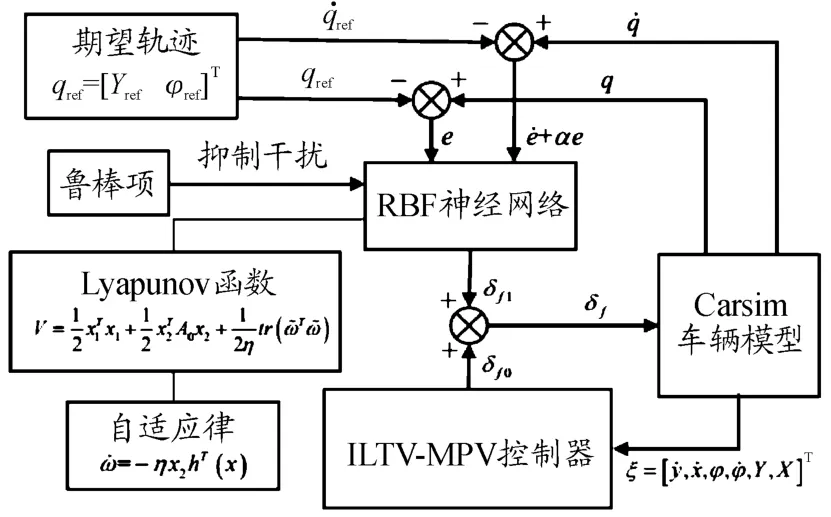
圖2 RBF魯棒-ILTV-MPC系統控制框圖

搭建Simulink和Carsim聯合仿真平臺，其中Carsim測試車型選用E-Class，SUV。設置了不同縱向行駛速度和路面附著系數的3種仿真工況：①v＝30 km／h，μ＝0.8（工況1）；②v＝50 km／h，μ＝0.8（工況2）；③v＝50 km／h，μ＝0.4（工況3），分別對優化前后3種控制系統進行不同工況下的雙移線［9］仿真對比。仿真過程中參數值見表1。

表1 仿真參數設置

控制器的軌跡跟蹤精度通過橫向位置及橫擺角的跟蹤誤差判定，無人駕駛車輛在3種雙移線仿真工況下的橫向位置Y隨橫向位置X跟蹤結果及誤差e1隨時間t變化如圖3、4所示。

由圖3、4可知：在工況1條件下，ILTV-MPC軌跡跟蹤控制器橫向位置最大誤差為0.125 7 m，經RBF自適應補償控制后減小至0.077 02 m，約38.73%，均方根誤差減小32.35%；經RBF魯棒優化控制后減小至0.039 68 m，約68.42%，均方根誤差減小60.29%；隨著速度的提高，誤差逐漸增大，在工況2條件下，與傳統ILTV-MPC相比，RBF補償-ILTV-MPC均方根誤差減小23.24%，RBF魯棒-ILTV-MPC均方根誤差減小49.01%。

圖3 橫向位置軌跡跟蹤結果

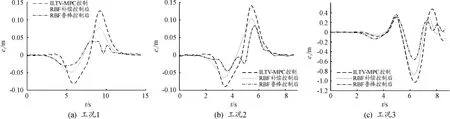
圖4 橫向位置誤差

在良好路面上，3種控制系統均可較好地完成雙移線路徑的軌跡跟蹤。RBF魯棒控制較RBF補償控制可進一步提高ILTV-MPC控制器的跟蹤精度。

在工況3條件下，仿真前期可較好地完成軌跡跟蹤，但后期由于控制量（δf）大幅度增大而出現較大偏差，雖車輛仍處于可控狀態，但易發生轉向失控等危險工況。與傳統ILTV-MPC相比，RBF補償-ILTV-MPC均方根誤差減小20.38%，RBF魯棒-ILTV-MPC均方根誤差減小45.86%。此時經RBF魯棒控制優化后的控制器在仿真前期精度雖有所下降，但在可接受范圍內。

當車輛以較高速度行駛在附著系數小的路面上時，3種控制系統在仿真后期均出現不同程度側滑；RBF魯棒控制較RBF補償控制可進一步減小ILTV-MPC控制器的誤差，減輕車輛側滑程度，在一定程度上提高車輛行駛穩定性，減少危險的發生。

車輛在3種工況下橫擺角φ隨橫向位置X跟蹤結果如圖5所示。

圖5 橫擺角軌跡跟蹤結果

由圖5可知，2種經RBF優化后的ILTV-MPC控制器，對橫擺角的跟蹤雖然精度有所提高，但仍存在一定時間的延遲。

此外，經多次仿真可知，ILTV-MPC軌跡跟蹤控制器最高安全縱向行駛速度為67 km／h，當速度超出最高安全速度時，橫向位置出現明顯偏差，車輛發生大幅度側滑；經RBF自適應補償控制后的控制器雖未有效提高臨界縱向行駛速度，但橫向位置偏差明顯減小，車輛側滑程度減弱；經RBF魯棒優化后的控制器最高安全縱向行駛速度可明顯提升至90 km／h。

3種控制系統不同縱向行駛速度橫向位置跟蹤結果如圖6所示。

圖6 不同縱向速度的橫向位置跟蹤結果

5 結論

設計了RBF補償-ILTV-MPC和RBF魯棒-ILTV-MPC 2種控制系統，與傳統ILTV-MPC軌跡跟蹤器相比，均可提高軌跡跟蹤精度。當以30 km／h速度行駛在良好路面時，與傳統ILTV-MPC相比，RBF補償-ILTV-MPC最大誤差減小約38.73%；RBF魯棒-ILTV-MPC最大誤差減小約68.42%。結果表明，經RBF魯棒控制優化后的ILTV-MPC控制器與經RBF補償后的控制器相比，可進一步減小軌跡跟蹤誤差，提高車輛的行駛穩定性。

但本研究僅考慮了3種工況，未能完全體現控制器所有工作環境，且優化后的2種控制系統對于橫擺角的跟蹤仍存在一定時間的延遲，導致誤差的產生；同時經RBF魯棒優化后的ILTV-MPC控制器臨界速度僅提升至90 km／h，對于高速下的無人駕駛車輛無軌跡跟蹤效果還需進一步改善。

下一步計劃對2種控制系統的實時性進行研究，并于多種工況下進行實驗驗證。