核燃料裂變破碎過程中靜力學和動力學受力分析的對比研究

王 斐，謝東升，張璦月，康 銳，吳 璐，潘虎成

（1.中國核動力研究設計院第一研究所，成都 610041；2.東北大學 材料學院 材料各向異性與織構教育部重點實驗室，沈陽 110819）

目前商用的核反應堆最核心的部件即為燃料組件［1-3］，而Zr［4-5］和UO2［6-8］是常用的核材料，其一般是由單片式的UO2／Zr［9-10］燃料板組成。該組件類似于金屬基的復合材料，即由微米尺度的UO2顆粒彌散分布于Zr基體合金的內部而成，所采取的制備工藝一般分為球磨制粉、混料、熱等靜壓以及后續的擠壓或軋制等大變形以降低孔隙率，從而達到控制形狀和控制性能的雙重目的。然而，在UO2／Zr單片式燃料板的實際服役過程中，往往面臨著嚴苛的高溫［11］、高 壓［12］和輻照［13-14］等環境，將不可避免的會在UO2內部或板內界面處的孔隙聚集大量的高溫裂變氣體，并在如此復雜的多場耦合作用下，對Zr合金的基體發生迭代式的爆炸沖擊作用，會有可能對Zr合金的基體帶來塑性損傷甚至破壞的風險。因此，系統研究UO2／Zr單片式燃料板服役過程中的裂紋擴展行為以及受力情況，對保障核反應的正常運行具有重要工程意義。

靜力學法［15-17］又稱“主應力法”，是在對實際工程問題進行簡化的基礎上建立平衡方程、屈服準則和邊界條件后求解變形力的一種近似方法。盡管有限元的動力學分析方法越來越被廣泛地應用于變形力的求解與預測［18-24］，靜力學法在工程上的應用也從未間斷［25-26］。靜力學的受力分析方法已被廣泛應用于擠壓、軋制、鍛造和拉深等塑性變形加工等問題上。譬如，鄧磊等［27］基于靜力學方法分析了鋁合金筋板構件擠壓變形過程的受力情況，其計算結果與數值模擬及試驗結果一致。張晗等［28］基于靜力學方法計算了圓棒料錐模拉拔力，結果表明，求解的拉拔力符合工程要求并能夠實現設備噸位的選擇。靜力學方法作為一種簡便的評估方法，可對受力情況實現快速有效的評估，周期短、成本低，因此在工程應用中始終受到學者們的青睞。

在本研究中，為了定量分析氣孔裂變爆炸過程中應力與變形情況，擬首先采用靜力學法對該工況進行應力預估，其次進行有限元的動力學研究以驗證靜力學分析的準確性。動力學方法主要涉及對建立的核燃料板進行溫度分析，根據溫度計算出沖擊壓力峰值，然后將該沖擊壓力變化作為沖擊載荷邊界條件應用于動力學沖擊分析，分析軟件為ANSYS LS-DYNA 19.0。核燃料板包殼采用Zr合金，芯體材料為UO2，各材料的力學性能如下表所示，本次有限元分析材料模型利用Johoson-Cook失效準則進行模擬。計算中所用的Zr合金參數選用的是經球磨制粉壓制后的Zr-2型的核用鋯合金，具體的工藝流程主要包括球磨、混粉、燒制和擠壓等工序，經制備加工后鋯合金的關鍵力學性能參數如表1所示。

表1 材料力學屬性

1 工程法靜力學近似分析

將氣體裂變過程簡化為球體受到內高壓發生塑性變形乃至破壞的過程，并利用工程法靜力學對該過程進行近似力學分析。

UO2／Zr燃料類似于金屬基的復合材料，即由微米尺度的UO2顆粒彌散分布于Zr基體合金的內部而成，經輻照后產生氣孔的形態普遍為球形，這一現象已經被掃描電鏡等分析測試方法普遍證實［29］。因此首先可以將核燃料假設為一個球體，內孔半徑為r0，球體半徑為R0（圖1所示），那么當內孔受內壓為p的條件下，如果發生塑性變形，則整個球體截面上沿半徑R方向上的點的應力大小可以通過工程法靜力學近似求解得到。

圖1 球體受力示意圖

根據靜力平衡條件，列半徑方向上的平衡方程為：

將式（1）進行化簡，忽略高階項影響，可得到簡化的平衡微分方程：

代入屈服準則公式：σθ-（-σr）＝σs，將其代入式（2）可得：

兩邊積分可得：

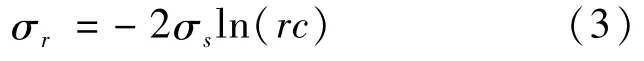
利用邊界條件，當r＝R0時，徑向應力為0，可得：

由式（4）可得當內層發生塑性變形時，r＝r0，此時內壓力p為：

由式（5）可見，氣體裂變過程中，二氧化鈾或者鋯合金發生塑性變形乃至塑性失效，主要與氣體大小和材料自身屈服強度有關，表現為自然對數關系，內層受靜高壓條件下易于失效，塑性失效破壞從內層逐漸外擴。

另外，當外部完全發生塑性變形乃至失效時，由于此時徑向應力為0，則整體受力可以看做一定壁厚的殼體，其壁厚為R0-r0，由平衡條件可得：

依據 σ1＝σ2＝σθ和 σ3＝0，代入屈服準則可得：

由式（7）可以看出，外壁發生塑性變形所需內層受內壓值比較大。由此可見，受單一的內靜高壓，不易使外層發生塑性變形乃至失效，但沖擊動力載荷卻有所差異。

2 數值模擬分析

2.1 力學分析有限元模型

燃料板外部為Zr合金包殼，內部為UO2芯體，同時夾雜以小型的氣孔。將氣孔、UO2和Zr基體均假設為球形，故符合軸對稱問題，可以簡化為平面問題，為實現在LS-DYNA中施加面載荷，以球心為中心點建立薄片三維體為幾何模型（厚度為0.005 mm），厚度方向僅劃分一層單元，進而大幅度減小有限元計算量，提升有限元求解速度。

本次氣體爆炸破碎有限元分析中，建立的有限元模型如圖2所示。如前所述，由于燃料板厚度相較于長度及寬度變化極小，可將整個模型簡化為平面應變問題，有限元網格劃分時板厚度方向為單層，又因UO2芯體在燃料板中彌散分布，可進一步將其簡化為軸對稱問題。尺度最小的三維模型由Zr合金基體、2個UO2芯體顆粒，裂變氣孔（包覆于UO2芯體）組成，建立的具有極薄厚度的1／4扇形薄板模型厚度為0.05 mm，Zr合金基體半徑為40 mm，UO2芯體顆粒內徑為1 mm，外徑為5 mm，與Zr合金基體接觸，裂變氣孔半徑為1 mm，包覆于UO2芯體，如圖2所示。

圖2 燃料板有限元模型

2.2 溫度分析及沖擊峰值確定

核燃料內的氣體在裂變過程中將產生高溫，高溫膨脹引起的脈沖載荷會對燃料基體產生顯著的沖擊作用。因此，裂變氣體可假設為內熱源，在溫度求解過程中，幾何模型可等效為圓柱體，根據軸對稱進行簡化并進行二維平面分析。內孔的半徑為1 mm，UO2的直徑為5 mm，Zr的尺寸為10 mm×20 mm，Zr的邊界溫度設定為300℃。依據裂變傳熱模型及分析計算，利用有限元軟件ANSYS LSDYNA 19.0可求解出核燃料板在裂變發生3 ms后的氣孔中心處的溫度6 117℃。

根據修正的范德瓦爾方程可以求得一定溫度和體積下的內部壓力水平，其中范德爾方程為：

其中，p為氣體壓強，即所求的沖擊載荷（Pa）；bV＝8.5×10-29m3，為裂變氣體Xe的范德瓦爾常數；V為氣體體積（m3）；hs＝0.6，為量綱為一化常數；N為總氣體原子數；k＝1.381×10-23J／K，為玻爾茲曼常數。將上述計算所得的溫度參數代入式（8），最終求得迭代式沖擊載荷峰值p約為800 MPa。溫度升高過程中，裂變氣體發生膨脹進而對周圍的UO2誘發內高壓，在較大的內壓力作用下UO2顆粒和Zr基體會被逐漸破壞。

2.3 Zr基體雙孔UO2顆粒核燃料板內氣體裂變過程的有限元分析

圖3所示為Zr合金基體雙孔核燃料板模型氣體裂變過程不同時刻燃料板等效應力的分布規律與塑性失效破碎情況。由圖3（a）可知，當核燃料發生裂變過程中，孔內氣體沖擊壓強達到峰值800 MPa時，最先受到破壞的是與氣孔接觸的UO2顆粒，在雙孔UO2顆粒尺度下，脆性較大的UO2顆粒絕大部分已破碎，圓孔周圍受力大小沿圓周方向基本相同，符合圓孔內高壓條件下力學分布特征。此時，塑性相對較好的Zr合金基體幾乎未發生變形，通過觀察彩云圖中顏色標尺，最大等效應力達到110 MPa左右，這與基體Zr合金材料的屈服極限94 MPa的數量級基本一致。另外，由于2個孔心連線上同時受到內高壓作用，引起圓心連線上應力集中，因此最大等效應力（棕色區域）區近似出現兩氣孔的連線兩側會隨著迭代式沖擊載荷的產生，應力值繼續增大，并且最大應力區逐漸向前推進，燃料板逐步發生破壞。

圖3 Zr基體雙孔UO2顆粒核燃料板裂變過程（不同時刻等效應力分布規律及基體塑性失效破碎情況）

在裂變、爆炸沖擊持續作用下，原UO2顆粒位置的孔受沖擊破壞程度進一步擴大（圖3（b））。在Zr合金基體上，裂變氣體沿之前初始時刻應力分布最大值的路徑前進破壞，并在核燃料板發生破壞的同時，由于裂變的鏈式反應特性，產生2次、3次等迭代式的裂變沖擊，圖3（b）中等效應力最大的區域（棕色區）在0.003 s這一時刻已經達到98 MPa左右，并不斷轉移前進。接近并高于Zr合金基體的初始屈服極限94 MPa，基體即將發生下一步的破壞。隨著沖擊載荷的持續作用，0.006 s時，裂變氣體沿之前中間時刻顯示的應力分布最大值的路徑前進，逐漸深入Zr合金基體的內部，在迭代式裂變沖擊的條件下，雙孔的破壞路徑向前推進，最終連接貫通，直觀上能看出破壞的主要路徑出現在兩裂變氣孔的連線上。這與初始時刻對破壞路徑的預測的板上受力特點相符。可以預測的是，當基體燃料板內存在更多的氣孔條件時，初始時刻孔的圓周率先產生塑性失效和破碎，隨著裂變過程進行，氣體沖擊持續作用下，圓心連線上易于產生應力集中，該應力集中會率先突破基體的抗壓強度使其破碎，基體內間隙越多，破碎的速度越快。

將UO2顆粒的屈服強度44 MPa、R0為5 mm，r0為1 mm代入式（5）可以得到內壓為141.63 MPa，略大于動力學求解結果，一方面說明靜力條件下裂變氣體使基體產生破碎需要更大的內壓，另一方面說明動力學條件下使材料發生破壞需要的沖擊載荷變小，當內部產生脈沖沖擊或瞬間載荷時，破壞性更大。最后靜力學計算的結果和動力學某一瞬間結算的結果相對誤差約20%，這說明靜力學分析方法能夠有效反映氣體裂變中產生的脈沖沖擊對基體的破碎趨勢。

3 結論

1）靜力條件下裂變氣體使基體產生破碎需要更大的內壓，而動力學條件下使材料發生破壞需要的沖擊載荷小，當內部產生脈沖沖擊或瞬間載荷時，破壞性更大。相比之下，靜力學分析方法能夠對反應氣體裂變中的受力情況進行有效評估。

2）二氧化鈾或者鋯合金發生塑性變形乃至塑性失效，主要與氣體大小和材料自身屈服強度有關，表現為自然對數關系，內層在靜高壓條件下易于失效，塑性失效破壞從內層逐漸外擴，如果僅僅是靜力作用很難使整個基體發生失效破碎。