區分二打一游戲競技者能力的測試用例研究

陳子鵬，李淑琴，鄭藍舟，孟 坤，丁 濛

（1.北京信息科技大學，北京 100010；2.感知與計算智能聯合實驗室，北京 100010；3.微智娛（北京）科技有限公司，北京 100010）

二打一是一種玩法簡單、娛樂性強的三人撲克牌游戲［1］。一局牌需3個玩家，一個玩家稱為地主，地主下家（逆時針第1個農民）稱為農民1，地主上家（逆時針第2個農民）稱為農民2。在每一局游戲中，地主獨立存在，而其他2名玩家以農民的身份組成一隊與地主對抗。地主、農民1、農民2依次出牌，3個人都進行了1次出牌定義為1個回合。地主的目標是以多種出牌組合方式首先打完自己的手牌；農民隊伍只要有1人比地主先出完手牌便可獲得游戲勝利，并計算本局小分。

2016年9月3 日，中國國家體育總局舉辦了首屆全國競技二打一撲克錦標賽（China competitive poker championship，CCPC）［2］，目前已舉辦了2屆。賽事沿用大師分系統［3-5］和復式賽制［1］，采取瑞士移位競賽辦法［3-5］和去紙牌化的桌面裁判員管理辦法，力求比賽公正與公平。首屆全國競技二打一撲克錦標賽歷經近1年時間，先進行全國大師分排行榜排名賽，再由全國大師分排行榜前2016名進行全國公開賽，最后選出108名選手進行全國錦標賽，這些選手經過為期2天緊張刺激的18輪比拼，最終決出本屆賽事的冠、亞、季軍。競技二打一比賽存在賽制冗長的問題，如果比賽所發初始手牌對選手的區分能力較強，則能夠以更少的輪數確保選手獲取唯一稱號。因此，對能夠區分二打一游戲競技者能力初始手牌的選取進行研究。

1 系統設計思想

一般將競技選拔試題對被試者情況分辨能力的大小稱為區分度［6］，主要用于評價以選拔為目的的選題。目前用于區分度分析的方法主要有經典測量理論［7-10］（classical test theory，CTT）和項目反映理論［11-13］（item response theory，IRT）。CTT以區分度選擇合格題目的過程需要經過統計考生得分、建立模型計算區分度、根據區分度選取合格的題目，通常的關注點是所有考生。然而競技二打一錦標賽以選拔高水平競技者為目的，需要確保排名靠前的競技者能夠獲得唯一的稱號和獎勵，因此CTT中常用的區分度評估模型不適用于解決競技二打一錦標賽的相關問題。本文中借鑒CTT框架提出選取合格的題目的步驟，其中創造性地提出了初始手牌的區分度（distinction of initial hand，DIH）的概念和算法，對區分二打一游戲競技者能力的測試用例進行研究。

定義1初始手牌

在出牌階段之前，3家（地主、農民1、農民2）分別持有的每1張撲克單牌的組合為初始手牌。

定義2測試用例

將經過區分度篩選的多個初始手牌稱為區分二打一游戲競技者能力的測試用例。

對于區分二打一游戲競技者能力的測試用例的研究主要分兩大方面，即根據二打一真實用戶打牌的行為數據，如何進行測試用例的選取，然后測試用例的可信度。

1.1 測試用例選取方法的研究

測試用例的選取思想：首先對大量真實用戶打牌行為數據進行分析及處理，計算每個初始手牌對應的得分概率分布；針對每副初始手牌，在比賽每輪使用與該初始手牌有著相同得分概率分布的初始手牌的條件下，計算此比賽最終的得分概率分布。基于此概率分布、比賽參賽人數、預先確定的比賽輪數、比賽需要確保選手獲取唯一獎勵的人數計算區分度，并進行非降序排序；選取區分度高對應的初始手牌作為測試用例。

1.1.1 初始手牌對應得分概率分布的計算

真實二打一用戶打牌行為數據有地主、農民1、農民2所持所有單牌組成的初始手牌信息，以及地主的得分。這些數據雜亂、無規律，本文中通過分析，計算初始手牌得分概率分布來得到初始手牌與得分之間關系。

使用的競技二打一的計分規則是勝負系數×加倍系數。當進攻方勝利，勝負系數為1，失敗，勝負系數為-1。加倍系數為n，n值為本副牌中打出的火箭數+炸彈數。火箭是雙王（大王和小王），炸彈是4張點數相同的牌。因此，得分分數所構成的集合為｛-n，…，-2，-1，0，1，2，…，n｝。

初始手牌的表示分為3個部分，每個部分放在一組中括號內，第1個中括號內為地主手牌，第2個和第3個中括號內為2個農民的手牌。例如“［TTKA379Q2D69K5Q94J6］［3JX8Q885TTK3265AK］［29Q435J426787JA7A］”，每個字符代表1張單牌，其中T代表單牌“10”，X代表單牌“小王”，D代表單牌“大王”。

對于牌庫（C1，C2，…，Cb），b為牌庫的初始手牌的數量，針對每副初始手牌Ci，其潛在的所有得分即潛在得分的分布Si＝（Si1，Si2，…，Sih），h為所有潛在得分分數的數量。進行y輪對局，每輪的對局得分Sij對應的出現次數cij加1，每個潛在得分出現的次數被記錄（ci1，ci2，…，cih），計算在不同分數上的得分概率Di＝（Pi1，Pi2，…，Pih），Di即初始手牌Ci的得分概率分布，其中

1.1.2 初始手牌區分度的計算

計算區分度的目的是選取初始手牌組成測試用例，以降低排名靠前的若干名選手分數重復的概率，針對競技二打一競賽的問題，對區分度有如下定義。

定義3初始手牌的區分度（distinction of initial hand，DIH）n人參賽，經過m輪比賽，保證前r名選手的得分不重復的概率。即希望前r名選手在錦標賽中獲取不同的分數。

對于牌庫（C1，C2，…，Cb），b為牌庫的初始手牌的數量，針對每副初始手牌Ci，假設其每輪比賽的得分概率分布都為Di＝（Pi1，Pi2，…，Pih），計算m輪比賽結束后的潛在得分的分布對應的不同分數上的得分概率，k為m輪比賽后所有潛在得分分數的數量。

下面通過1個例子進行詳細說明。例如，比賽共有玩家9人，即n＝9。比賽輪數2輪，即m＝2。比賽需要確保獲取唯一獎勵的數量r為2。若此比賽所分發牌的初始手牌得分概率分布如表1所示，即潛在得分的分布S＝（-2，-1，1，2），計算其對應的得分概率分布P＝（0，0.6，0.4，0），對于此次比賽該初始手牌的區分度計算步驟如下。

表1 某初始手牌的得分概率分布

假設2輪比賽完全獨立，則比賽結束后的潛在得分的分布為S（2）＝（-4，-3，-2，-1，0，1，2，3，4），統計比賽結束后的得分概率分布P（2），如表2所示，P（2）＝（0，0，0.16，0，0.48，0，0.36，0，0）。依次計算第1名獲得-2，-1，0，1，2，3，4分的情況，即公式中共需要累加項數k＝7。當第1名獲得4分時，第2名得分的取值情況是-4＜M2＜4，M2共有7種取值，即集合M共有7個元素，因此區分度的第1層累加和的第1項如式（3）所示。按上述步驟在計算剩余的6項，區分度結果為0.358。表明初始手牌的區分度比較低，不能用來比賽。

表2 2輪比賽結束后此初始手牌的得分概率分布

1.1.3 測試用例的選取

選取測試用例的目的是應用于實際比賽中，以降低賽程所耗費的時間。選取測試用例的方法是根據擬定的比賽輪數、參賽人數和唯一獎勵的個數，計算各初始手牌的區分度，并進行非降序排序；選取區分度高對應的初始手牌作為測試用例，初始手牌的數量與比賽輪數相同。測試用例的選取算法的偽代碼如下：

其中，append（）函數是在列表的最后添加新的元素，sorted（）函數為列表進行排序，len（）獲取列表的長度。

1.2 測試用例的驗證

檢驗測試用例的設計思想：指定若干名比賽狀態穩定，并有區分度的選手，進行玩家固定成為某一角色的方式的比賽。固定比賽輪數，即比賽共有m輪，先給選手按隨機分發初始手牌進行比賽。每輪比賽統計選手得分，第d輪比賽的選手得分記為（Sd，1，Sd，2，…，Sd，n），n是選手的人數，根據（Sd，1，Sd，2，…，Sd，n）為選手進行排名，每人的名次記為（Od，1，Od，2，…，Od，n），Od，i∈（1，2，…，n）。同時，若從第y名開始在有k個人得分相同，此k個人的排名都記為y+1，且第y+k名選手的名次記為y+k即 （Od，y-1，Od，y，Od，y+1，…，Od，y+k-1，Od，y+k）＝（y，y+1，y+1，…，y+1，y+k）。根據排名為每位選手對第d輪比賽進行積分，即選手的排名分（Rd，1，Rd，2，…，Rd，n），Rd，i＝2×（n-Od，i+1），并統計每個選手的m輪比賽結束的總排名分只要不同選手的總排名分不相等，選手就是可區分的。上述的比賽共舉辦w場，計算排名前r個選手可區分的概率，記為P1。再按用測試用例分發初始手牌進行比賽，比賽共舉辦w場，同樣計算排名前r個選手可區分的概率，記為P2。比較P1與P2值的大小，如果P2比P1值大，就說明測試用例是可信、實用的。

如何選取“比賽狀態穩定且據有區分度的選手”是難點。因為真人選手比賽時間一長就不能保證其比賽狀態的穩定性。另外，選手的區分度需要通過上百甚至千場的線上對局才能評估，因此，找真人做實驗不太現實。為此，本文中提出通過具有區分度的多個“斗地主AI程序”來代替真人選手進行實驗的方案。

筆者所在研究團隊曾針對地主、農民1、農民2分別開發了多款斗地主AI程序。他們沒有考慮叫分功能，通過人類打牌日志基于CNN模型訓練出牌策略，能夠達到著名競技二打一牌手的水平，相關的具體信息參見文獻［14-16］。

算法1獲取具有區分度的“AI打牌組合選手”

輸入：a個地主的“斗地主AI程序”，（l1，l2，…，la）；

b個農民1的“斗地主AI程序”，（f11，f12，…，f1b）；

d個農民2的“斗地主AI程序”，（f21，f22，…，f2d）；

比賽擬定的參賽人數，u。

輸出：具有區分度的多個“AI打牌組合選手”。

步驟1通過地主、農民1、農民2的交叉組合，獲得若干由1個地主、1個農民1和1個農民2組成的“AI打牌組合選手”，（G1，G2，…，Ga×b×d），Gi＝（li，f1i，f2i），共計a×b×d組。

步驟2隨機生成m副初始手牌（H1，H2，…，Hm），隨機初始手牌的生成見算法3。

步驟3i＝1，即選取第1副初始手牌H1

步驟4每個“AI打牌組合選手”打完這副牌Hi；統計當前輪比賽“AI打牌組合選手”的地主的得分，并計算當前“AI打牌組合選手”的地主的總得分。

步驟5i＝i+1；

步驟6if i＞m then跳轉至步驟4，否則跳轉至步驟7。

步驟7統計打完m副初始手牌的每個“AI打牌組合選手”的地主的總得分（T1，T2，…，Ta×b×d）進行排序，記錄其最大值Tmax和最小值Tmin。計算每個組（G1，G2，…，Ga×b×d）的得分率（P1，P2，…，Pa×b×d），即

步驟8以（P1，P2，…，Pn）的最大值1和最小值0劃分區間，將［0，1］的區間均分為w個（I1，I2，…，Iw），Ii＝（（i-1）×（1／w），i×（1／w））。w為將指定的測試AI的數量。

步驟9得分率落在同一個區間“打牌組合選手”被分到同一個集合中（C1，C2，…，Cw）。

步驟10隨機從每個集合中挑選1個“AI打牌組合選手”，組成1組具有區分度的測試者。

初始手牌的生成算法如下所示：

算法2隨機生成初始手牌。

輸入：54張撲克單牌。

輸出：3家（地主、農民1、農民2）的初始手牌。

步驟1對54張撲克單牌進行洗牌，獲得被打亂順序的54張撲克單牌的列表（c1，c2，…，c54）。

步驟2i＝1，即取單牌c1。

步驟3當i mod 3＝1即i除以3所得余數是1時，分發給地主，當i mod 3＝2時，分發給農民1，當i mod 3＝0時，分發給農民2。

步驟4i＝i+1

步驟5if i＜52 then轉至步驟3，否則跳轉至步驟6。

步驟6剩余的3張撲克單牌（c52，c53，c54）歸地主所有。

2 系統實現

使用Intel Xeon E5-2640 CPU，NVIDIA 1080Ti GPU和Ubuntu 16.04服務器系統的服務器。

2.1 生成初始手牌庫及生成測試用例

首先建立初始手牌庫，并從初始手牌庫中選取初始手牌組成測試用例。競技二打一游戲平臺提供了500萬條游戲日志，統計每副初始手牌所出現的次數，為了使初始手牌得分數據更加真實，所以本文中只考慮打牌次數大于50次的初始手牌，共有1 925副。1 925副初始手牌在單次對局中打出的火箭數+炸彈數的上限為6，因此，初始手牌的得分分布將被表示為（-6，-5，-4，-3，-2，-1，1，2，3，4，5，6）。

先根據式（1）計算1 925副每個初始手牌的得分分布。再根據算法1，通過初始手牌區分度的式（2）計算每副初始手牌的DIH，對初始手牌按DIH進行非遞減排序，依據比賽輪數選取靠前的若干副初始手牌即測試用例。

例如，對于比賽人數為8，比賽輪數為4，唯一獎勵數為2的比賽，選取出的測試用例如表3所示。

表3 比賽人數為8，比賽輪數為4，唯一獎勵數為2的比賽的測試用例

2.2 驗證測試用例的可信性

利用已有的斗地主3個角色的出牌模型，分別訓練了9個地主、7個農民1和7個農民2 AI玩家。使用算法3隨機生成了4 000副初始手牌。通過9個地主、7個農民1和7個農民2的交叉組合，共擁有9×7×7＝441個“AI打牌組合選手”。

由于競技二打一的冠軍稱號最為重要且唯一，固定唯一獎勵的個數為1，替換參賽人數n和比賽的輪數m，對給選手按隨機分發初始手牌進行的比賽和按用測試用例分發初始手牌進行的比賽分別模擬了多場，在參數不同的比賽中，選取測試用例所用的DIH相應的參數也隨之改變，從而對測試用例進行驗證，同時分析DIH的參數間的關系。對于同一種比賽，共模擬1 000次，每次模擬依據擬比賽人數n通過算法2選取具有區分度的“打牌組合選手”。多種比賽的不重復概率見表4，表序中r是唯一獎勵個數；n為參賽人數；m為比賽人數；P1是給選手按隨機分發初始手牌進行比賽，在m輪比賽結束后，前r名參賽選手比分不重復的概率；P2是按用測試用例分發初始手牌進行比賽，在m輪比賽結束后，前r名參賽選手比分不重復的概率；（P2-P1）／P1是P2相對于P1的提升比率。

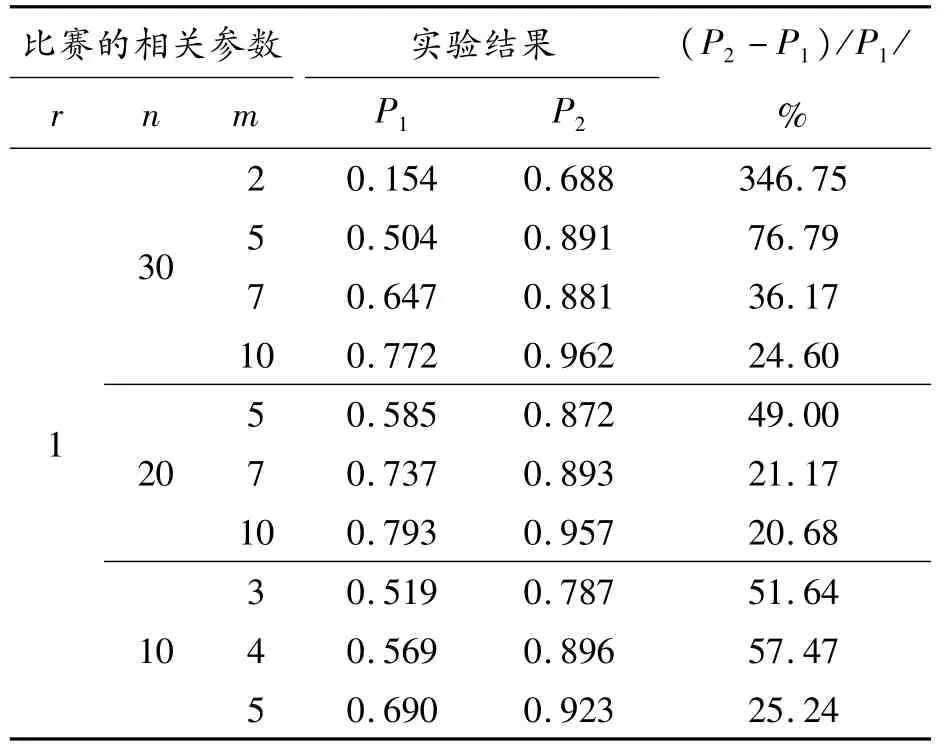
表4 測試用例的可信度的驗證

通過實驗結果發現：

1）當m相對于n很小時，如m＝2，r＝1，n＝30時，選牌的隨機性很大，同時選取的測試用例穩定，結果的提升率為346.75%，因此，表明了測試用例選取方法的有效性。

2）接下來通過結果對參數之間的關系進行分析，以n＝30，r＝1為例對按用測試用例分發初始手牌進行比賽不重復的概率，提升比率與m的關系進行分析。當m增加時，不重復的概率增加，但是P2相對于P1的提升率在降低即使用測試用例的有效性降低，因此選擇一個適中的m是最佳的選擇。

3）固定r＝1和m＝5，分析n和實驗結果的關系。當n＝10時，P1相對于P2的提升率為25.24%，當n＝20時，P1相對于P2的提升率為49%，當n＝30時，P1相對于P2的提升率為76.79%，P1相對于P2的提升率隨著n的增加而增加。即當參賽人數增加時，測試用例的有效性增加。

綜上，不論比賽的相關參數，按用測試用例分發初始手牌進行比賽的不重復概率都高于給選手按隨機分發初始手牌進行比賽的不重復的概率，因此選取測試用例的方法是有效的，可以用來解決比賽賽程過長的問題。

3 結論

提出通過給出具有較高區分度的初始手牌用于比賽發牌階段，以減少比賽輪次的解決方案，并提出初始手牌區分度的算法。為驗證測試選取用例的有效性，提出采用多個具有不同區分度的“AI打牌組合選手”進行模擬比賽。實驗結果表明測試用例的選取方法是有效的。但是初始手牌區分度的算法的時間復雜度和比賽唯一獎勵的個數呈指數級增長，因此不適用于大型比賽計算，算法需要進一步優化。另外，區分度的參賽人數與比賽輪數、獲獎人數等存在一定關系，在接下來的工作中還需要對三者具體關系進行研究。