大型索網反射面天線空間動力學分析*

廉蔭虎，倪 崇，李博韜，王飛杰，杜敬利

（1. 西安電子科技大學，陜西 西安710071；2. 北京空間飛行器總體設計部，北京100094）

引 言

隨著天文學、物理學等學科的發展，航天學科的研究目標日趨復雜，航天任務變得更加艱巨，大型可展開索網反射面天線的設計也變得更加困難，往往要求天線向著柔性變大、尺寸變大的趨勢發展[1]。目前大多數航天器主要由剛性主體和一些大尺寸、低質量、低剛度的撓性附件組成。航天器在軌運行時，有可能產生柔性附件彈性變形與航天器主體剛性運動的耦合問題[2]（學術上稱之為多體動力學的剛–柔耦合問題），這將會對天線的結構性能及射頻性能造成極大影響。

自20世紀60年代以來，P. W. Linkins，R. E. Skelton，R. E. Roberson等人開始就航天器存在的剛性本體與柔性太陽翼剛–柔耦合問題進行了大量的研究。20世紀70年代，美國科學家就大型可展開索網反射面天線與衛星本體的耦合問題做了大量工作，并成功研制了口徑為60 m的大型柔性天線。20世紀90年代，文獻[2]結合柔性動力學理論對衛星在軌時的姿態穩定與運動控制調整問題進行了深入分析。

國內在相關領域的理論研究方面也有了一定的技術積累，并在平面陣合成孔徑雷達天線的展開動力學方面以及帶有柔性太陽翼帆板的衛星動力學耦合方面開展了大量的理論研究，這些都為可展開索網反射面天線–太陽能帆板–衛星耦合動力學的研究奠定了基礎。但到目前為止，周邊桁架式索網反射面天線與衛星本體之間的耦合動力學問題仍是航天工程設計中的難題，還需要科研人員努力突破該瓶頸。本文以某星載大型可展開索網反射面天線為切入點，對其進行了空間動力學分析。

1 整星系統的有限元模型

整星系統由兩側太陽翼、伸展臂、天線以及衛星本體組成。太陽翼分別位于衛星本體南北兩側，對稱地連接在衛星本體上；伸展臂一端連接在衛星本體上，另一端與天線桁架相連。整星系統的有限元模型如圖1所示。

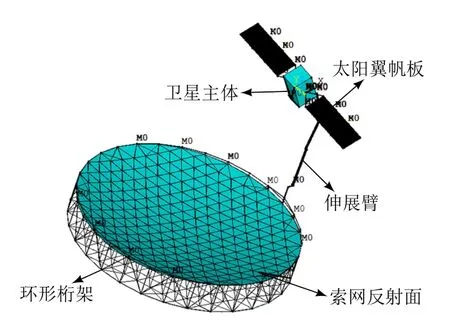
圖1 整星系統有限元模型示意圖

利用ANSYS軟件建立該整星有限元模型時，采用自底向上、分模塊建模的方式[3]。首先通過結構參數分別建立好天線周邊桁架、伸展臂和太陽翼帆板模塊；然后根據天線網面的結構參數計算反射面節點坐標，將節點依次連成索單元和膜單元后，將索單元的邊界索連接至周邊桁架上進行“找形”分析，尋找最佳平衡態位置，這樣便建成了天線模塊的有限元模型；最后建立局部坐標系，使得各個模塊有限元模型的建模坐標系與局部坐標系一致，進而將各部分模型組裝到一個總體坐標系下。整星有限元模型各部分采用的單元見表1，所涉及的整星模型的部分物理參數見表2。

表1 整星系統各部分所用單元

表2 整星模型的部分物理參數

2 整星系統和天線的模態分析

在機械振動理論中，機械結構的動力學響應狀態與其本身固有的模態特性有關。對機械結構固有模態特性的分析稱為模態分析，包括對固有頻率、振型和振型參與系數等的分析，是動力學分析的基礎。

整星系統在軌運行時處于太空漂浮狀態，為模擬這種特殊狀態，在模態分析里使整星模型處于無約束的狀態下，又因為模型有索結構，所以對整星系統的分析為有預應力的模態分析。模態分析前10階頻率見表3，前6階振型如圖2所示。

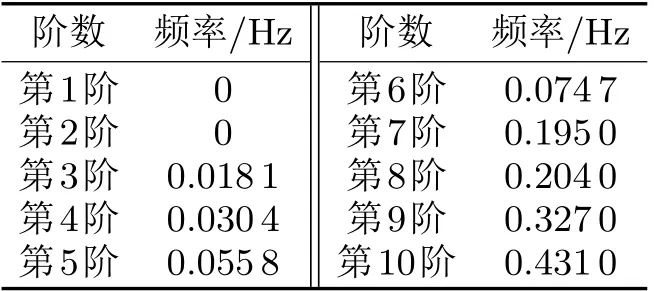
表3 整星系統前10階模態頻率

由振動理論[4]可知，整星系統的前6階模態應該為剛體運動，其頻率應該都為0。然而，由表2可知，整星系統第3階到第6階的頻率不為0。從圖2可知，整星系統第3階到第6階除了剛體位移外，柔性支撐臂和天線還發生了彈性變形，整星系統的運動不再是單純的剛體運動，還發生了剛–柔耦合情況，稱之為剛–柔耦合模態。

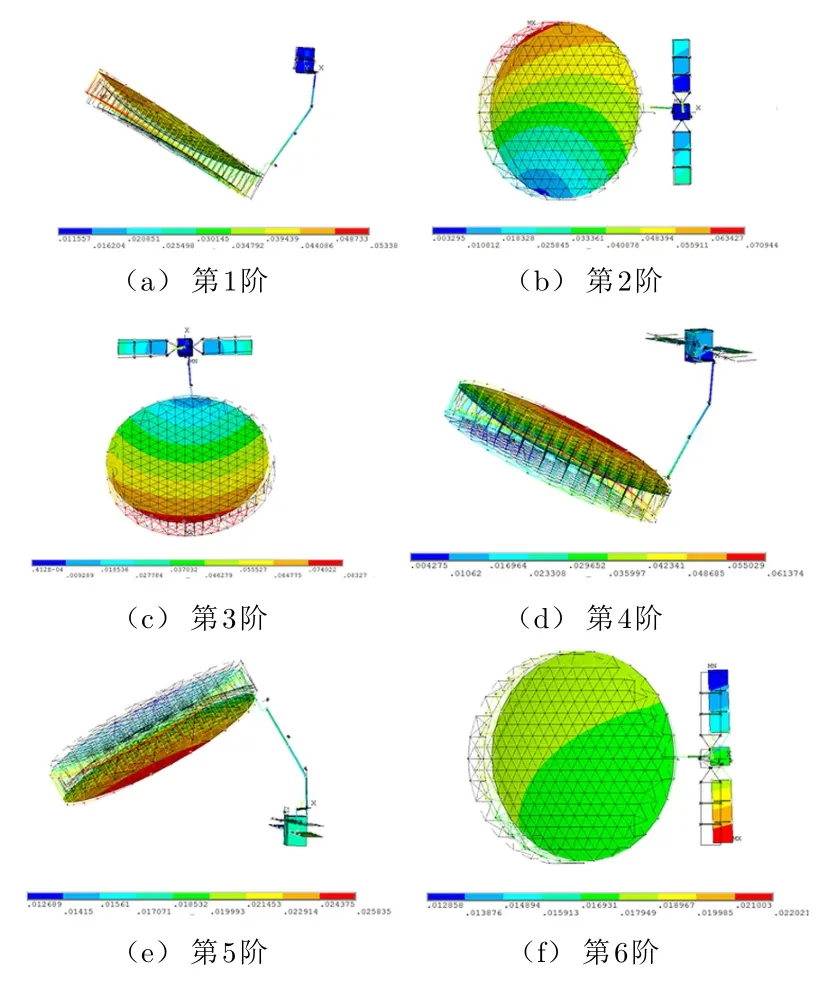
圖2 整星系統前6階振型示意圖

整星系統從第7階到第9階模態為太陽翼和天線的振動模態。第7階頻率為0.195 Hz，其振型主要是天線的搖頭以及伴隨著太陽翼繞其陣面垂線方向的轉動；第8階諧振頻率為0.204 Hz，其振型主要是左側太陽翼在其陣面方向的擺動；第9階諧振頻率為0.327 Hz，其振型主要表現為右側太陽翼在其陣面方向的擺動并伴隨有天線的上下擺動（即天線的“點頭”）。第9階之后的模態信息主要表現為太陽翼和天線的高階振型的組合，因篇幅所限，不做贅述。

在天線和伸展臂剛度較大即整星系統為近似剛體時，整星系統前6階固有頻率應該都近似為0，但由于整星系統本身由大量細桿和柔性繩索組成，且具有較大的伸展空間，再加上伸展臂剛度有限，使得天線和伸展臂的剛度遠小于衛星的剛度，使得整星系統第3階到第6階的剛體模態呈現出較強的非線性特征，所以系統的這4階頻率不為0。整星系統的這種特性使得天線不能實時跟隨衛星大范圍的剛體運動和小范圍的調姿運動作相應的運動。由于天線的運動與衛星的剛體運動不同步，因此衛星大范圍的剛體運動或調姿運動會導致天線和伸展臂的彈性變形，進而引起天線和伸展臂的彈性振動，這種振動必將反作用于衛星載體，引起衛星的姿態振蕩，這就是所謂的剛–柔耦合現象。要使系統最終穩定下來，就要通過衛星的平衡裝置來抑制天線的振動，這就要消耗大量能量，從而影響衛星的運行壽命。當衛星的平衡系統無法抵消這種反作用時，衛星就會失穩，系統也就失效了。因此對于大型衛星–天線系統，剛–柔耦合影響分析對衛星姿態控制系統的穩定性設計是十分重要的[5]。

3 整星系統的動力學響應分析

通過整星系統的模態分析獲得了系統的固有特性，即整星系統的固有頻率和各階振型，為系統的動力學響應分析奠定了基礎。

動力學分析用來求解隨時間變化的載荷對結構或部件的影響。與靜力學分析不同，動力學分析要考慮隨時間變化的力載荷以及它對阻尼和慣性的影響。系統的動力學響應不僅由系統所處的動力學環境（沖擊、振動和噪聲）決定，而且與固有的阻尼和慣性有關。ANSYS根據所建立的有限元模型、邊界條件和施加在模型上的載荷建立系統的動力學方程：

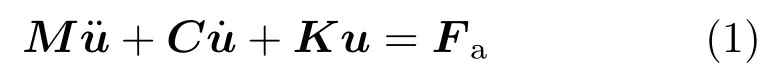
式中：M 為質量矩陣；C 為阻尼矩陣；K 為剛度矩陣；對應自由度的項分別是加速度¨u、速度˙u和位移向量u；Fa是施加在系統上的載荷。

衛星在軌道上運行時，除了受所處的特殊熱環境影響外，還會受到其自身機動工況（如噴氣推進和太陽翼驅動等）的影響。這里對建立的整星系統有限元模型進行動力學響應分析，通過軟件仿真衛星的噴氣推進工況，具體分析衛星在受到噴氣負載情況下時域和頻域的振動特性以及天線反射面的形面精度隨時間的動態響應。

衛星的噴氣推進一般在衛星的質心處施加一定量的力和力矩組合，結合本文的具體工況，噴氣推進為周期性載荷，噴氣脈沖時間為0.5 s，間隔時間為5 s，噴氣點火的累計時長為10 s。噴氣動力以方波的形式施加，施加時間為(5+0.5)×19+0.5 = 105 s，仿真時長為750 s。施力點和觀察點在模型中的位置如圖3所示。由于其噴氣載荷是周期性載荷，這里只給出其前17 s的力和力矩示意圖（圖4）。

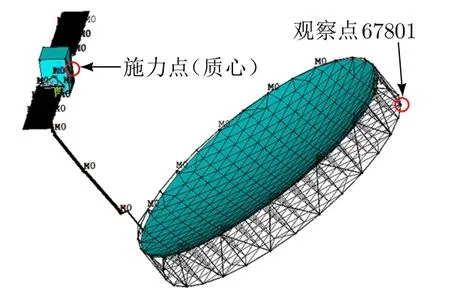
圖3 施力點和觀察點位置示意圖

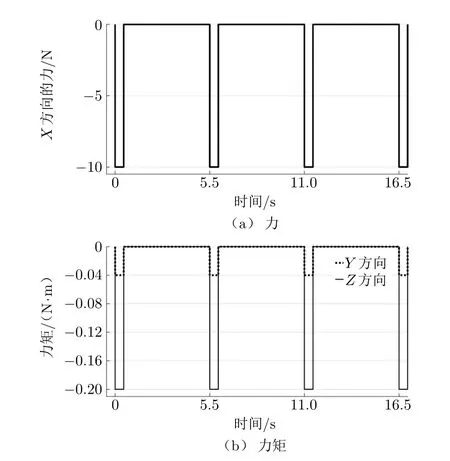
圖4 噴氣推進前17 s的力和力矩示意圖

為模擬衛星在太空的漂浮狀態，分析時不施加任何方向上的約束。模型在不施加約束時存在剛體位移，因此分析時在模型關鍵節點上建立隨動坐標系，去除衛星的剛體位移，最終得到衛星節點上的彈性變形響應。通過分析得出，離衛星最遠端節點67801（見圖3）的變形量最大。圖5和圖6分別為該節點的變形曲線示意圖和自由振動曲線示意圖。

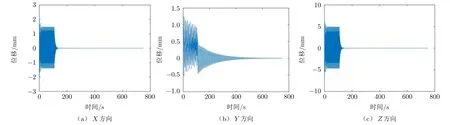
圖5 節點67801的變形曲線示意圖

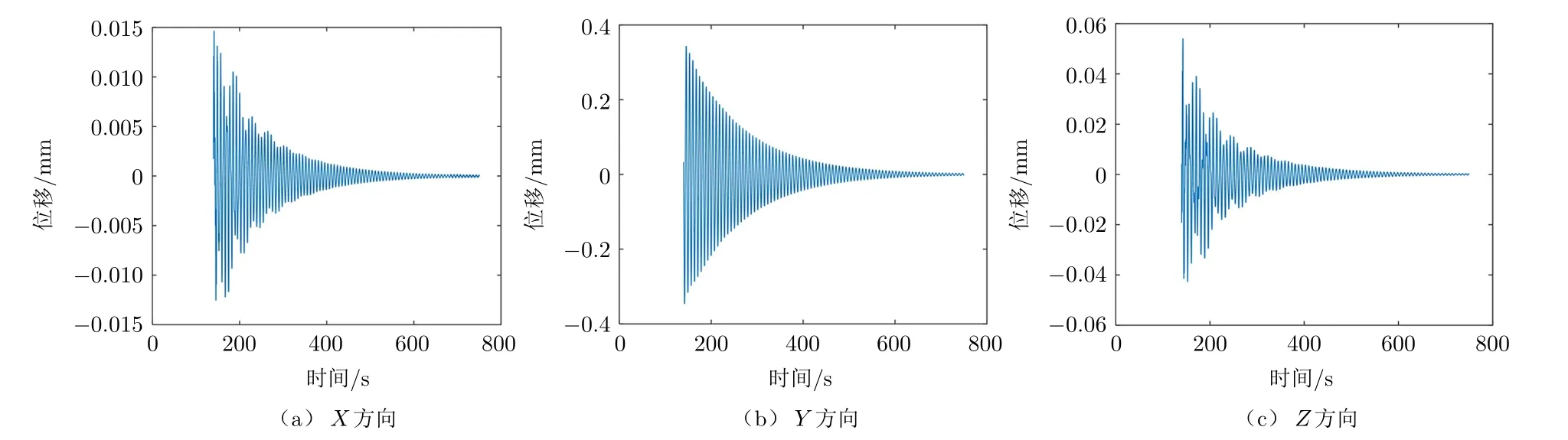
圖6 節點67801的振動曲線示意圖

為更好地分析天線的振動特性，對節點67801的自由振動曲線作傅里葉變換，得到如圖7所示的自由振動頻域示意圖。從圖7可知，其響應頻率為0.069 Hz和0.427 Hz。

圖7 節點67801在X，Y，Z 向的自由振動頻域

根據以上分析及振動響應的時域和頻域特性曲線，可以得出以下結論：

1）在受到沖擊載荷時，節點67801的變形量急劇增大，X 向和Z 向的變形量最突出，變形的最大幅值為6.94 mm，但撤去外力后，其變形量趨于穩定。

2）雖然Y 向的變形幅值相對于其他方向不大，但撤去外力后，其自由振蕩的幅值明顯，而且幅值的降速也非常緩慢（從撤去外力到幅值減小到0.1 mm用時192 s）。

3）從圖7可知：在自由振動過程中，X 和Z 向的振動頻率為0.427 Hz，與整星系統的第10 階頻率（0.431 Hz）相吻合；Y 方向的頻率為0.69 Hz，正好與整星系統的第12階頻率（0.682 Hz）相吻合，同時，第12階振型主要表現為天線搖頭。從中可以看出，整星系統受到的沖擊載荷主要激起了系統第12階模態的振動。為分析天線在此沖擊載荷下的結構性能變化，這里主要給出在動態載荷下天線反射面的形面精度隨時間變化的規律（圖8）。

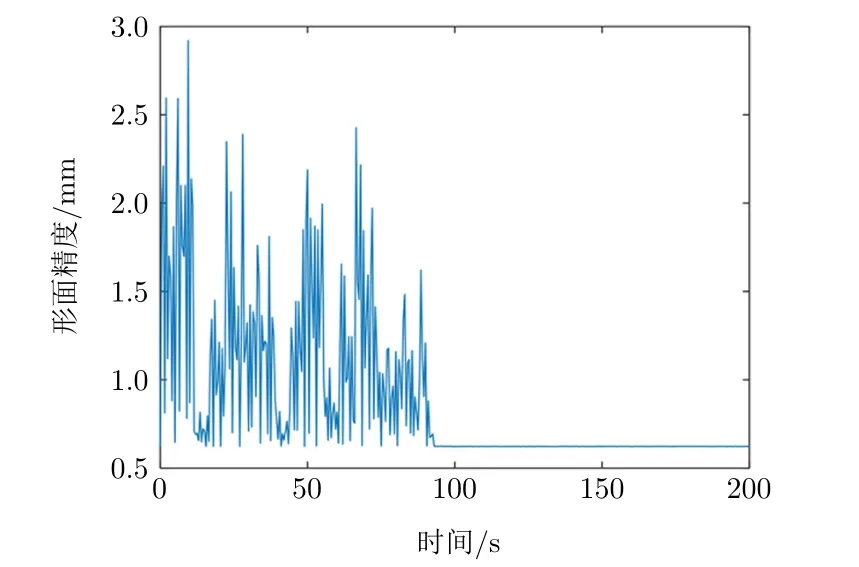
圖8 天線的形面精度隨時間變化曲線示意圖

在施加載荷100 s后，天線基本上已經穩定下來，故此處分析200 s內天線的形面精度。如圖8所示，施加噴氣動力時，由于天線變形量增大，反射面的形面精度變化劇烈，最大的形面精度出現在第11 s，此時均方根誤差達到了2.85 mm；停止施加噴氣動力時，由于天線節點變形量減小，網面的形面精度又回到了設計值0.5 mm。

4 結束語

本文針對某星載大型可展開索網反射面天線，對其有限元模型進行了模態分析，闡述了其基本模態信息；然后模擬衛星在太空漂浮狀態下受到噴氣推進工況時的動力學響應，從時域和頻域分析其最大變形點處的振動特性；最后為分析天線的結構特性變化，給出了網面的形面精度隨時間變化的曲線。通過分析得出以下結論：

1）從模態分析結果可看出，整星模型前6階模態為剛體模態，但第3到第6階模態存在剛–柔耦合振動模態，從第7階開始為太陽翼和天線系統的振動。

2）從整星系統的噴氣推進動力學仿真結果可看出，天線在噴氣推進作用下變形較大，網面的形面精度也會受到較大影響。