空間機械臂精度分析研究與軟件實現

王友漁，唐自新，李德倫，曾 磊，張昕蕊，王 念

(1.北京空間飛行器總體設計部空間智能機器人系統技術與應用北京市重點實驗室，北京100094；2.北京衛星制造廠，北京100094)

1 引言

空間機械臂是空間站建造、運營、維修及拓展等過程中不可或缺的關鍵設備，其精度是設計制造需要考慮的重要因素，也是開展高精度動力學與控制技術研究的基礎。

最具代表性的空間艙外機械臂是加拿大研制的大型遙操作臂系統(SSRMS)，安裝在國際空間站上。根據載人航天任務規劃，中國空間站也將配備一個大型七自由度空間站機械臂，目前已完成鑒定產品研制，開展了大量的精度設計、分析與驗證工作。當前空間機械臂精度研究主要集中在針對地面機械臂建立位姿誤差模型，并進行相關的誤差分析上，研究方法具有一定的片面性，分析的誤差因素不全面。影響空間機械臂精度的因素很多，如制造及裝配的誤差、關節間隙誤差、控制誤差、計算誤差等地面機械臂常見誤差源，還有環境溫度影響等空間機械臂特有誤差源。特別是關節作為中國空間站大型空間機械臂的核心部件，采用多級傳動系統設計方案，如果采用傳統國家標準進行計算，其計算過程十分繁瑣復雜，很多參數需要查表，對標準制度的依賴性很強。王棟等在考慮關節誤差因素基礎上，建立了對誤差有綜合評價性能的機械臂精度模型。于登云、劉志全等針對大型空間機械臂關節重點研究了關節誤差及其柔性變形影響，并應用于機械臂動力學建模及控制。何曉煦等為了提高飛機裝配機器人末端定位精度，提出了基于誤差相似度的殘差補償方法，實現對機器人的幾何參數誤差辨識及誤差補償，并完成了試驗驗證。龔星如、柯振輝等以六自由度串聯機器人為實驗對象，分別開展了機器人誤差因素和誤差源的綜合分析，并對特定構型的機械臂末端誤差進行了試驗研究。Adel、Song等針對特種工業機器人精度預估及誤差補償技術開展研究工作，并用于提高機器人控制精度。劉冬雨等開展了七自由度機械臂在軌操作末端誤差的尺寸鏈分析，并利用手眼相機完成機械臂末端維修操作精度標定策略研究及試驗驗證。然而上述研究均未考慮空間環境及構型影響，不適用于特定構型工況任務的高精度操作預估分析需求。

為了實現空間機械臂在軌不同任務構型工況的快速高效精度分析，本文綜合各因素影響，采用綜合分析方法進行機械臂精度建模，并根據數學模型編寫機械臂精度分析軟件，以輔助機械臂精度設計分析并指導工程制造及裝配，最后通過實例計算驗證所建數學模型與軟件的有效性。

2 空間機械臂精度影響因素分析

影響空間機械臂的精度因素主要包括以下4類:

1)參數因素:主要包括制造及裝配的誤差引起的關節轉角輸出誤差、關節轉軸偏差、桿件長度誤差以及基座和目標點安裝位置誤差等；

2)負載因素:包括桿件彈性變形、關節傳動剛度等，該部分為動態影響因素，不影響穩態到位精度；

3)計算誤差:包括控制計算誤差、數據舍入誤差等，該部分相對其他誤差影響很小；

4)環境因素:包括溫度影響，噪聲擾動影響等。

根據對系統影響規律分析，上述因素可分為系統誤差和隨機誤差。其中加工制造誤差、基座和目標點安裝位置誤差等屬于系統誤差，可以通過精測標定手段加以補償，但是對于關節轉角輸出誤差、關節轉軸偏差、控制計算誤差以及環境因素影響等隨機誤差很難消除。

根據上述分析可知，機械臂精度主要由關節轉角輸出誤差，關節轉軸誤差以及連桿幾何誤差等構成。其中環境溫度影響可以等效分解到上述環節，也可以統一通過整臂熱分析計算。

1)各關節的轉角輸出誤差:各個關節的轉角輸出誤差對末端的影響效果與末端端點到關節轉軸的垂直距離成正比。由于機械臂關節狀態在變化，因此各關節轉角的轉角輸出誤差對末端的影響因子也會隨著各關節到機械臂末端端點的距離變化而變化。該項影響因子定義為α。

2)各關節的轉軸偏差:即旋轉連桿除了在垂直于轉軸的平面上旋轉外，還在過轉軸的平面上轉動角度。該影響因素也與關節轉軸與回轉中心與旋轉連桿中心線的交點到機械臂末端端點的距離成正比。該項影響因子定義為β。

3)連桿幾何誤差:主要考慮環境溫度影響導致的連桿熱變形誤差，空間機械臂連桿一般選用碳纖維材料時，該項誤差相比關節引起誤差可以忽略，但是關節等采用金屬材料的需要重點考慮。

關節精度通常包括上面提到的關節轉角輸出誤差和關節轉軸偏差，而關節轉角輸出誤差又包括傳動誤差和回程誤差。影響嚙合齒輪傳動精度即傳動誤差的因素有:齒輪的剛度、齒輪的制造裝配誤差。而輪齒的厚度、齒輪副的中心距變化、齒輪副回轉中心的平行度誤差、輪齒齒向誤差、軸承間距和齒廓誤差等都會對齒輪副側隙有影響，另外環境溫度也會對齒輪的側隙產生影響。齒輪的側隙和單向傳動誤差組成齒輪的回程誤差。這些因素相互之間有耦合作用。

傳動系中各級齒輪對輸出精度的影響因子與各級齒輪轉速和輸出轉軸轉速之比成反比，因此首先考慮的是提高輸出軸附近齒輪的轉角輸出精度。根據齒輪的一般設計方法來選擇齒輪的傳動精度等級，設計齒輪側隙的時候要綜合考慮到空間環境溫度變化影響以及側隙對齒輪回程誤差的影響。

3 空間機械臂精度建模

本文通過機械臂運動學理論并綜合概率學知識建立考慮因素全面的空間機械臂精度分析模型。首先采用Denavit-Harterberg(D-H)參數法定義運動學模型中各名義參數關系，然后對運動學方程進行推導和分析，最終得到機械臂運動學模型。

某大型空間站七自由度機械臂全長約為10 m，包括7個關節和2個末端，其運動學參數坐標系關系如圖1所示，參數數值參見表1。

圖1 機械臂運動學參數坐標系Fig.1 Reference frame ofmanipulator kinematics

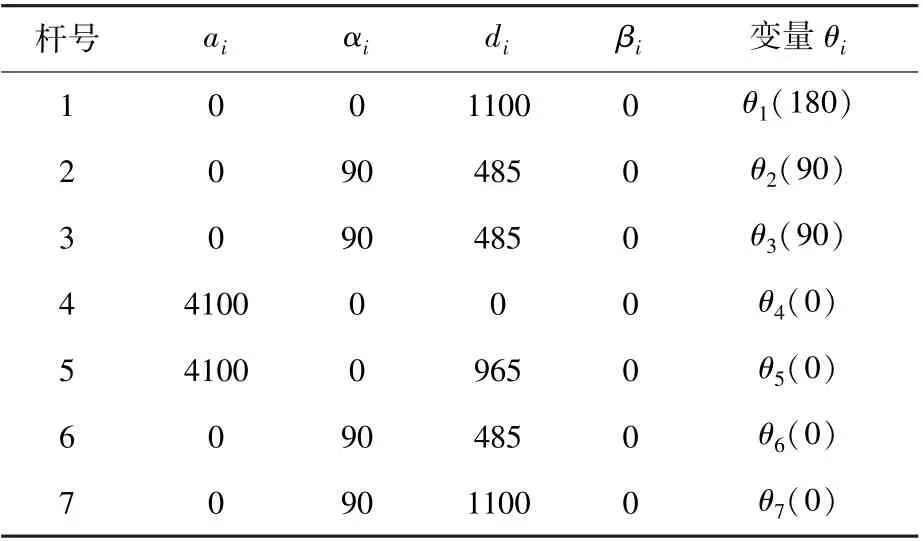
表1 某大型空間站機械臂運動學參數Table 1 Kinematic parameters of a large spacemanipulator

其中:θ為第i(i＝1，2，3)關節的關節角(兩連桿法線的夾角)；d為兩連桿的相對位置；a為兩連桿的公法線距離；α為繞X軸由Z軸轉到Z軸的偏角；β為繞Y軸由Z軸轉到Z軸的偏角。并規定軸線平行關節d為0，軸線非平行關節β為0。

采用D-H參數建模方式建立廣義坐標變換矩陣，根據平移和旋轉矩陣的先后關系，可以采用Tran(a，0，0)Rot(x，α)Tran(0，0，d)Rot(z，θ)Rot(y，β) 以 及 Rot(z，θ)Tran(0，0，d)Tran(a，0，0)Rot(x，α)Rot(y，β)兩種模式的建模方式。本軟件保留兩種建模方案，在實例計算時采用后者建立的相鄰連桿間廣義坐標變換矩陣如式(1):

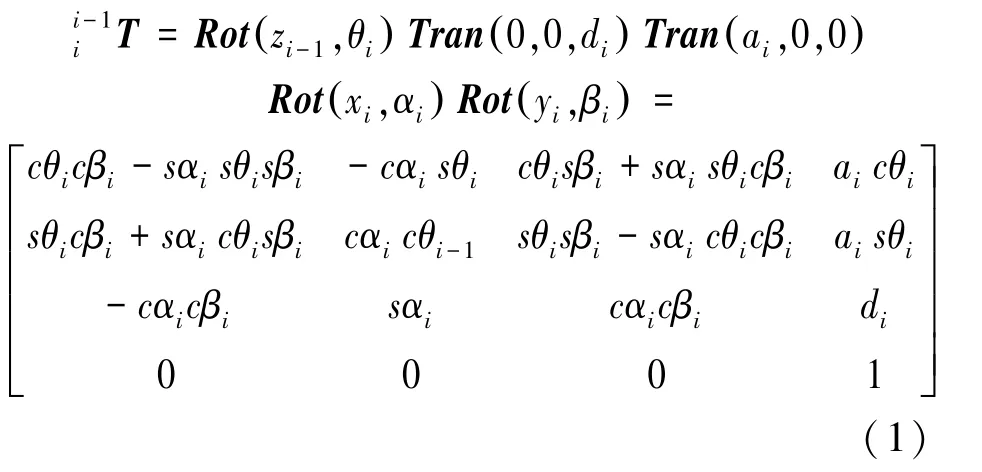
根據機械臂末端誤差定義，可得機械臂連桿i相對連桿i-1的誤差模型如式(2):

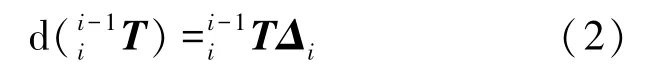
其中Δ為運動學微分變換矩陣，可表示為式(3):

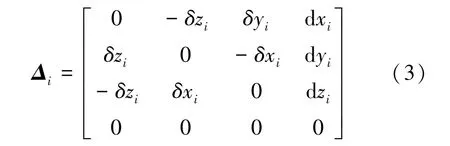
其中d x，d y，d z和δx，δy，δz分別表示連桿i末端的位置和姿態誤差。

在實際過程中由于Δθ、Δd、Δa、Δα、Δβ等機械臂各參數誤差都很小，可以采用連桿間的微分運動學模型來代替，對坐標變換矩陣進行全微分，代入式(2)和(3)可得式(4):

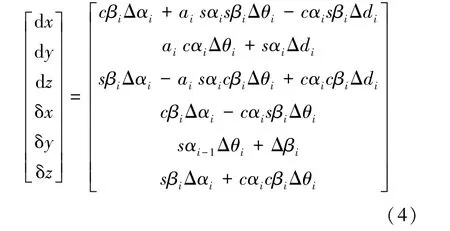
通過累計各連桿誤差形成機械臂末端總誤差模型如式(7):

4 空間機械臂精度分析

4.1 關節傳動誤差分析

如果關節齒輪傳動裝置的組成零部件沒有制造和安裝誤差，在工作時也沒有熱變形、彈性變形等的影響，那么在關節傳動過程中，輸入軸轉角φ和輸出軸轉角φ之間應該符合理想的線性關系曲線，即φ和φ之比應該是一個常數，等于總傳動鏈的傳動比，即i＝φ/φ。 實際上，各零部件不可能沒有制造、裝置誤差，而且在工作過程中還會產生熱變形和彈性變形。因此在傳動過程中輸出軸的轉角難免有誤差。

轉角誤差的角值φ與其在分度圓上的線值Δ之間的轉換關系如式(8):

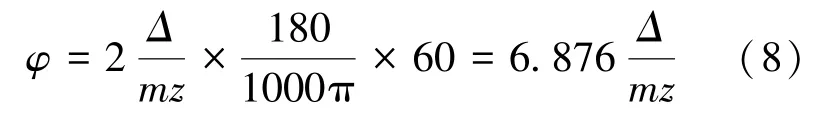
式中，m為模數，z為齒數。本文綜合國家標準規定的計算方法，提出基于統計學原理的關節精度計算方法。首先根據齒輪精度影響因素分析，區分出影響關節傳動準確性誤差的因素，主要包括切向綜合偏差、齒距累積偏差、徑向跳動、徑向綜合偏差、公法線長度變動影響因素。然后利用概率統計理論，針對影響傳動準確性誤差因素進行逐步分析:先計算影響傳動準確性的單個齒輪傳動誤差，重點考慮制造裝配誤差影響；最后計算整個傳動鏈的傳動誤差，重點考慮傳動過程載荷作用變形影響。通過跳過現有方法中對齒輪副傳動誤差的計算，避免了定軸輪系中傳動副誤差累計且不易區分的現象。

基于概率分析齒輪傳動誤差時，由于傳動誤差屬于隨機誤差，因此應該先列出傳動誤差的基本綜合式，然后利用概率統計理論，列出傳動誤差的統計學算式，求出均值和方差，最后通過式(9)所示求出考慮3倍方差的關節傳動系統的傳動誤差。

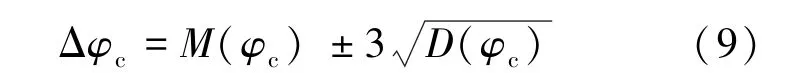
式中，Δφ為綜合轉角誤差；M(φ)為多次計算轉角誤差φ的均值；D(φ)為多次計算轉角誤差φ的方差。

4.2 機械臂整體精度分析

一般來說，給定運動學D-H參數誤差值，機器人在不同位姿下，末端的位置誤差不同。同樣，在同一姿態下，當各個D-H誤差參數值在給定范圍內變化時，末端位置誤差也不同。根據現有機械臂D-H參數模型可以得到機械臂特定姿態特定誤差時的末端誤差，但是不能給出在機械臂工作空間內，給定關節傳動誤差范圍時的最大誤差。

空間機械臂末端誤差可以表示為如式(10)、(11)函數:

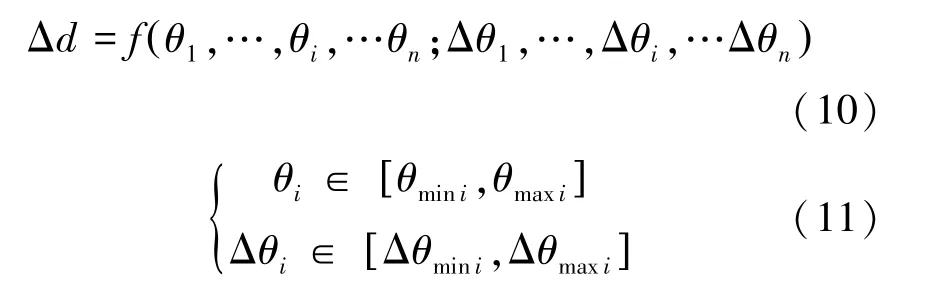
其中θ表示各關節的轉角值，Δθ為各關節的 轉 角 誤 差 大 小。 若 令 x ＝(θ，…，θ，…θ；Δθ，…，Δθ，…Δθ)則可以將機械臂末端最大誤差值問題轉化為非線性最優化問題，如式(12)所示。

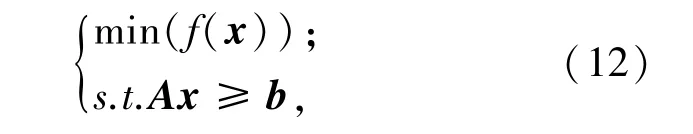
其中A為4n行2n列矩陣，前2n行為單位矩陣，后2n行為單位矩陣乘以-1，b為4n維列向量，前2n個分量分別為θ，…，θ，…，θ，Δθ，…，Δθ，…，Δθ。 后2n個分量為-θ，…，-θ，…，-θ，-Δθ，…，-Δθ，…，-Δθ。

對于該類型的最優化問題可以采用梯度投影法等進行求解。針對空間機械臂工作可靠性及安全性高的特點，本文提出一種求解系統最大末端誤差的方法，以保證足夠的安全距離。首先按照工作空間要求設置適合的關節角組合，確定機械臂末端姿態，然后在該姿態下搜索誤差組合值，使末端姿態最大。關節傳動誤差對機械臂末端端點位置誤差的影響程度取決于末端端點到關節原點或轉軸的距離，據此設計適合空間機械臂末端誤差搜索算法如下:

如圖2所示，θ是第i個關節轉角，p是第i＋1個坐標系的原點，d是第i＋1個坐標系的原點到基坐標原點的距離。當第i個關節轉角變化時，第i＋1個坐標系原點的軌跡為圓弧。基坐標系原點到圓上點的距離有且只有一個最大值。其距離的變化規律類似正弦函數。用一般的二分法難以找到其最大值。可以考慮先把整個角度變化區間等距離取20個角度值，對每個角度值求第i＋1個關節坐標系原點到基坐標系原點的距離。然后比較這些距離，找到距離最大值對應的關節值。以該關節綜合傳動誤差范圍為搜索區間，然后利用三分法搜索距離最大值。

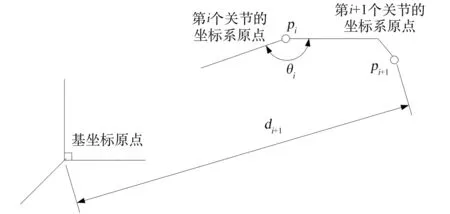
圖2 機械臂末端誤差搜索算法示意圖Fig.2 Diagram of search algorithm for end accuracy error of spacem anipu lator

5 算例分析

空間機械臂精度分析軟件由軟件界面和分析算法庫兩部分組成，根據分析層次其界面又分為關節精度分析界面和機械臂系統精度分析界面。用戶通過軟件界面輸入相關設計參數或指標，并點擊界面命令按鈕，程序就會調用算法庫對用戶指定類型關節及機械臂進行精度分析。

5.1 關節精度分析

采用齒輪鏈傳動誤差分析方法建立的關節精度分析軟件框架總體布局如圖3所示。

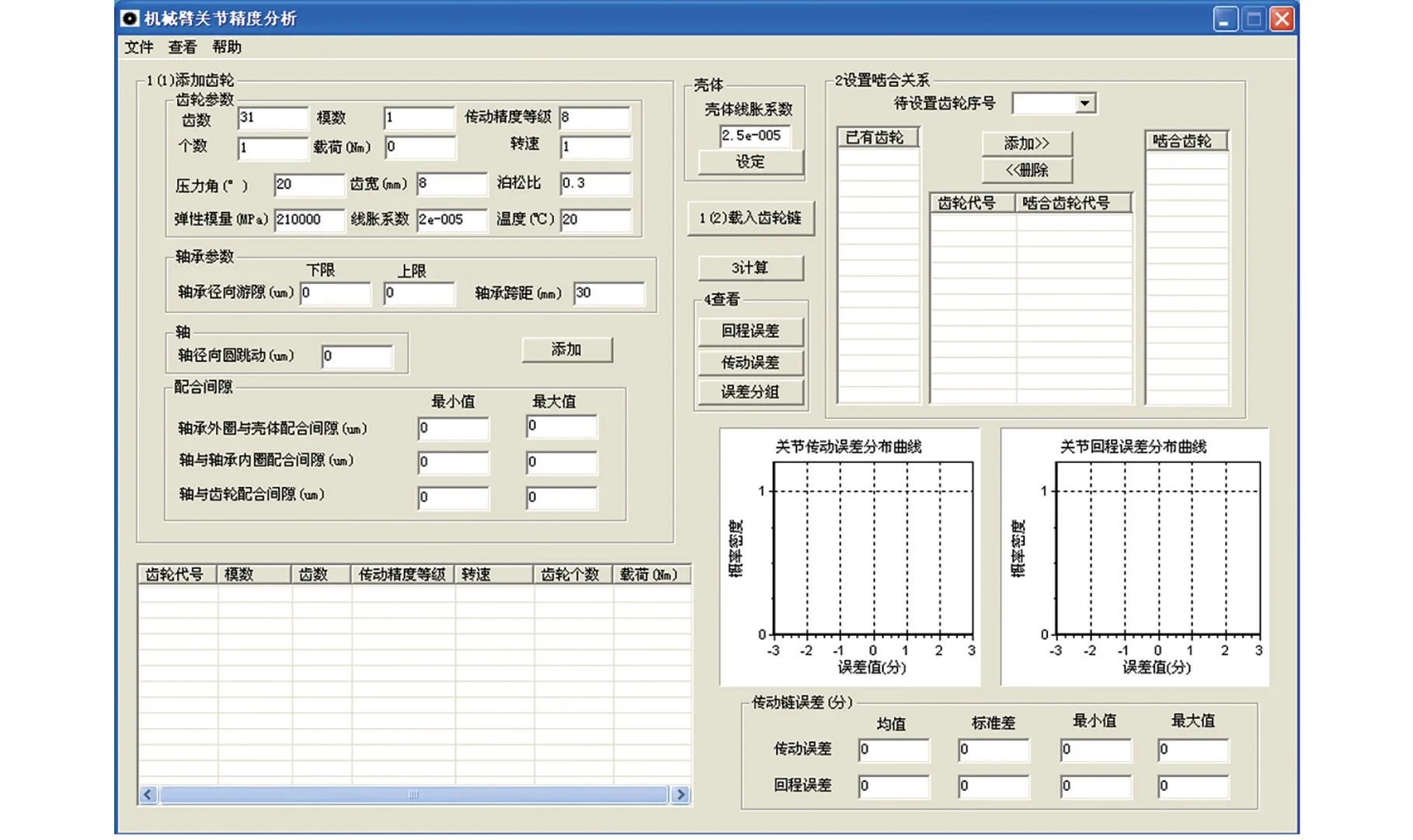
圖3 關節精度分析界面Fig.3 Interface of joint accuracy analysis

關節精度分析界面可以分為四大區域:添加關節齒輪區、編輯關節齒輪區、齒輪嚙合關系設置區和計算結果顯示區。其中個數是指在同一轉速級別，具有該類型參數的齒輪的個數；載荷為該齒輪承受的轉矩，單位為Nm；配合間隙是考慮到齒輪安裝時的裝配誤差，可以為齒輪孔與齒輪軸的配合間隙，齒輪軸與軸承內圈的配合間隙，軸承內圈與外圈的配合間隙，軸承外圈與殼體的配合間隙，界面中各間隙順序沒有影響；泊松比和彈性模量是齒輪的材料屬性；壓力角為齒輪分度圓上壓力角，默認值為20°。在使用關節精度分析軟件過程中，先設置好各編輯框的值，然后單擊添加按鈕，則可添加相應參數的齒輪到關節齒輪鏈當中。齒輪添加區域增加的齒輪會在關節齒輪鏈編輯區域中顯示出來。并按照添加順序設置齒輪代號。

在給定機械臂關節結構參數、材料特性、加工精度及潤滑特性等輸入條件下，利用本軟件的關節精度分析模塊進行計算，即可得到關節輸出軸的傳動誤差和回程誤差均值，標準差以及最大值和最小值。該大型空間機械臂關節精度分析的軟件計算界面及結果參見圖4及表2所示。根據分析計算可得關節最大總轉角誤差約6′。

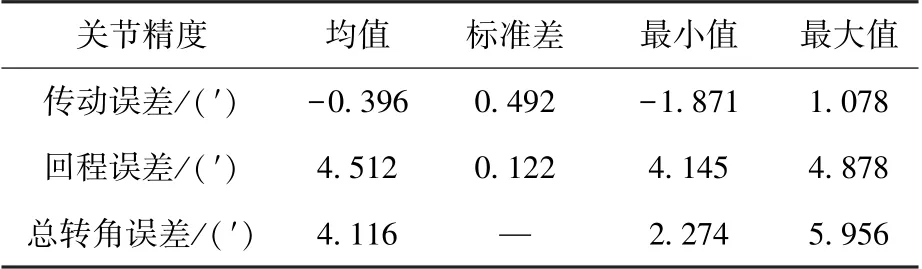
表2 關節精度計算結果Table 2 Calculated results of joint accuracy

圖4 關節精度計算結果Fig.4 Calculated results of joint accuracy

5.2 機械臂精度分析結果

機械臂末端最大誤差搜索頁面如圖5所示。其關節設置區域的主要功能是設置各個關節的轉角范圍和各項角度誤差范圍。先選中關節序號下面的一個序號，然后再后面的編輯框中輸入相應的數字，點擊設定按鈕，則設定一組值。之后列表框中會顯示各轉角范圍以及在當前轉角范圍和轉角誤差范圍狀態下使末端位置誤差最大的關節轉角值以及關節誤差值。同時最下面的理論位姿矩陣和實際位姿矩陣也會顯示最大誤差值時的位姿矩陣，右下角的編輯框中得到最大誤差距離預估值。

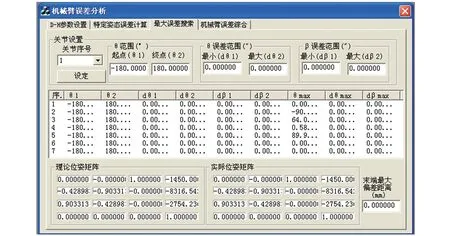
圖5 最大誤差搜索界面Fig.5 Interface ofmaximum error search

根據本機械臂精度分析軟件進行分析，其中關節轉角誤差按5.1節的計算結果設置。在關節轉角±180°范圍約束和關節誤差范圍約束條件下，基于最大值搜索算法計算分析得到的機械臂系統末端精度結果界面如圖6所示，可以得到該大型空間機械臂末端最大位置誤差為23.02 mm，對應該七自由度機械臂構型為各關節角度依次為[0°，-180°，90°，0°，90°，180°，-180°]。

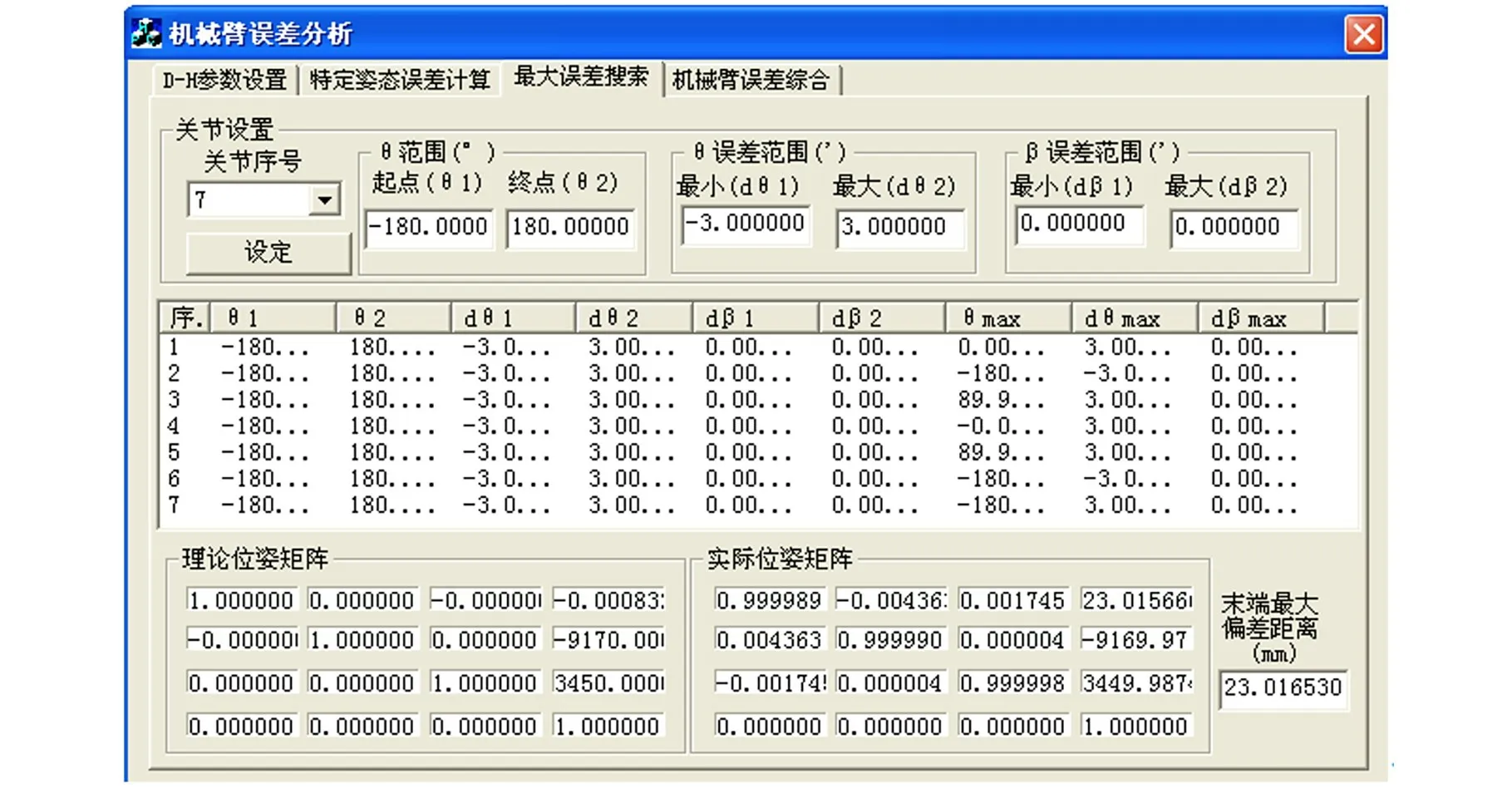
圖6 機械臂精度計算結果Fig.6 Calculated results ofmanipulator accuracy

已知該機械臂關節及末端外殼材料為鋁合金，熱膨脹系數23×10/K，溫差范圍80℃；臂桿材料為碳纖維，熱膨脹系數接近0，其變形忽略不計。根據空間環境溫度場熱變形理論分析計算可知，溫度影響導致的等效關節轉角誤差約0.8′，機械臂末端位置誤差約6.5 mm。

因此考慮空間環境情況下，該空間機械臂的末端最大位置誤差約為23.02＋6.5＝29.52 mm，能夠滿足中國空間站任務要求。

5.3 試驗驗證

按照GB_T20868-2007《工業機器人＋性能規范及其試驗方法》標準，采用激光跟蹤儀在二維氣浮平臺對該機械臂工程樣機的末端精度進行了測試，如圖7所示。通過數據分析確定氣浮臺測試情況下機械臂工程樣機末端位置誤差為22.2 mm，與未考慮溫度影響前的機械臂末端最大位置誤差預估值23.02 mm接近，誤差不超過5%，證明了該精度分析方法的可靠性和準確性。

圖7 空間機械臂工程樣機Fig.7 Prototype of a spacemanipulator

原機械臂的精度設計分析周期需要一周左右時間，現采用該軟件可以在2 h內完成分析。因此采用該軟件能夠快速預估空間機械臂末端精度并應用于實際在軌任務，其計算結果可以作為最大末端誤差進行保守預估，從而保證空間機械臂實際運行過程中預留足夠的安全距離。

6 結論

本文提出了一種大型空間冗余機械臂精度快速預估分析方法；設計的軟件經試驗測試，能綜合考慮關節輸出精度、各關節轉軸誤差以及環境溫度等因素影響，可實現在軌不同任務構型工況的空間機械臂末端精度快速預估，提高空間機械臂精度設計分析效率。