裝備剩余壽命預測與維修保障策略研究

顧曦文，溫 瑞，吳 琦

（91351 部隊）

0 引 言

傳統的裝備維修保障通常根據大量裝備損傷或壽命的歷史統計規律配置大量的維修保障資源并指導維修保障實踐，由于缺乏對裝備個體技術狀態的準確判斷，致使難以對維修保障需求進行實時準確的預計，同時各層級維修保障資源之間缺乏靈活的協同機制，致使整個維修保障體系中經常面臨局部維修保障能力過剩或不足的情況，傳統裝備維修保障呈現費用高、效能低的特點。裝備自主維修保障與感知響應保障理念強調以網絡為中心，結合故障預測健康管理技術與分布式決策技術， 通過實時獲取維修保障需求、動態配置保障資源來提高裝備可靠性， 縮減保障規模，降低保障費用與保障風險[1-3]。

實現裝備自主維修保障 （Autonomic Logistics System，ALS）需要兩個關鍵要素（維修保障需求的準確預測能力和全局范圍內動態響應維修保障需求）來重構維修保障資源的決策能力。有些學者在相關方面作了一些探索，如文獻[3-5]分析了裝備故障預測信息與備件庫存策略以及供應鏈的關系， 并提出了相應的單部件系統換件維修模型與供應鏈優化設計模型；文獻[6]采用復雜網絡理論與方法構建了基本的自適應保障的網絡模型，并對重要的特征參數進行了統計分析與對比。 整體來說，目前關于裝備維修決策、備件管理、資源分配的研究相對比較多，但其理論系統均建立在傳統的維修保障體制與模式基礎之上。為了適應網絡化作戰及精確保障的要求，特別需要對將裝備故障預測信息與維修保障網絡深度結合的自主維修保障體系進行研究。

本文針對上述存在的問題以武器裝備管理過程的實際情況為例， 提出了一種新的裝備剩余壽命預測與維修保障策略。 采用神經網絡模型及遺傳算法求解了在該情況下最優的裝備剩余壽命預測與維修保障策略。 分析該類裝備關鍵部件壽命分布的規律性，預測分析其相應的剩余壽命，并根據該類裝備關鍵部件更換與庫存的相關數據， 在保證部件可靠度不低于要求的條件下，研究其最佳的更換時間、備件訂購時間和訂購數量，使得總費用最低，最終針對該類裝備，制定一個長期的、最經濟與可信度高的維修保障策略。

1 裝備失效函數

在武器裝備管理中，定期對其關鍵部件的綜合性能指標X 進行檢測，間隔時間為15 天。 當綜合性能指標X 達到失效閾值ω=0.7 時，則認為該部件壽命終止。

首先根據之前儲存的裝備信息部件為樣本，認為性能指標X 為隨機變量， 計算其在不同時刻性能指標隨機變量AXj 內元素滿足的分布。 以此為基礎，求解不同時刻性能指標X 大于失效閾值ω 的概率，得到部件失效分布函數。

由于不同時刻部件的性能指標符合正態分布，但是不同時刻， 性能指標符合的正態分布的參數不相同。 對于已知的162 個不同時刻的參數AXj，正態分布參數μj，σ2j的估計值如圖1 所示。

圖1 正態分布參數μj、σ2j在不同時刻估計值

由于j 時刻的正態分布參數μj，σ2j都是在離散狀態下的估計值。 對于可靠性指標的分布函數X(t)，需要求解在連續情況下可靠性指標X 服從的分布函數，即裝備失效函數。

本文采用對離散的估計參數μj，σ2j擬合的方法將離散的參數連續化。 使用多項式擬合估計參數μj，σ2j的變化，當多項式次數較高時，可以得到較好的擬合結果。然而當時間變量超過被擬合數據中所給的范圍后， 高階多項式擬合結果可能出現很大的振蕩，這是高階多項式擬合的最大問題。為了避免擬合函數在后期的發散，我們盡量使用三階以下的多項式進行擬合。 鑒于參數μj，σ2j隨時間的變化比較復雜，三階以下的多項式很難較好的擬合情況，本文對參數μj，σ2j進行分段， 分別用分段函數進行擬合。 用MATLAB的cftool 曲線擬合工具箱， 對分段的參數μj，σ2j進行擬合：

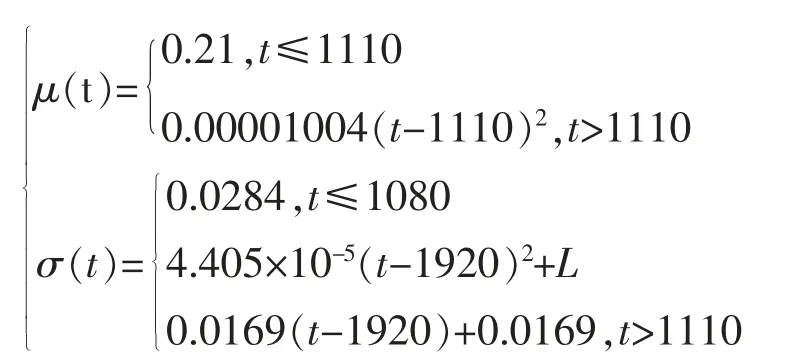
擬合函數如圖2 所示。

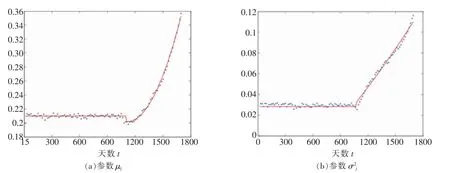
圖2 正態分布參數μj、σ2j的擬合

則部件失效的概率分布函數F（t）可表示為:

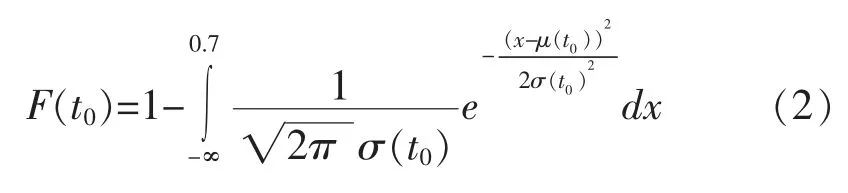
2 裝備壽命預測

可通過上述已知的觀測樣本中得出的壽命規律，來預測現存20 個裝備的剩余壽命。

由于整個性能指標退化過程視為馬爾科夫過程，只需將20 個部件給出的最后性能指標值和對應天數，即可和之前的數據相對比，通過聚類算法將20 組數據歸類， 得出此題中20 個部件所屬的剩余壽命分布規律（見圖3），利用相應類型的分布規律得到剩余壽命，進而得到可信度。

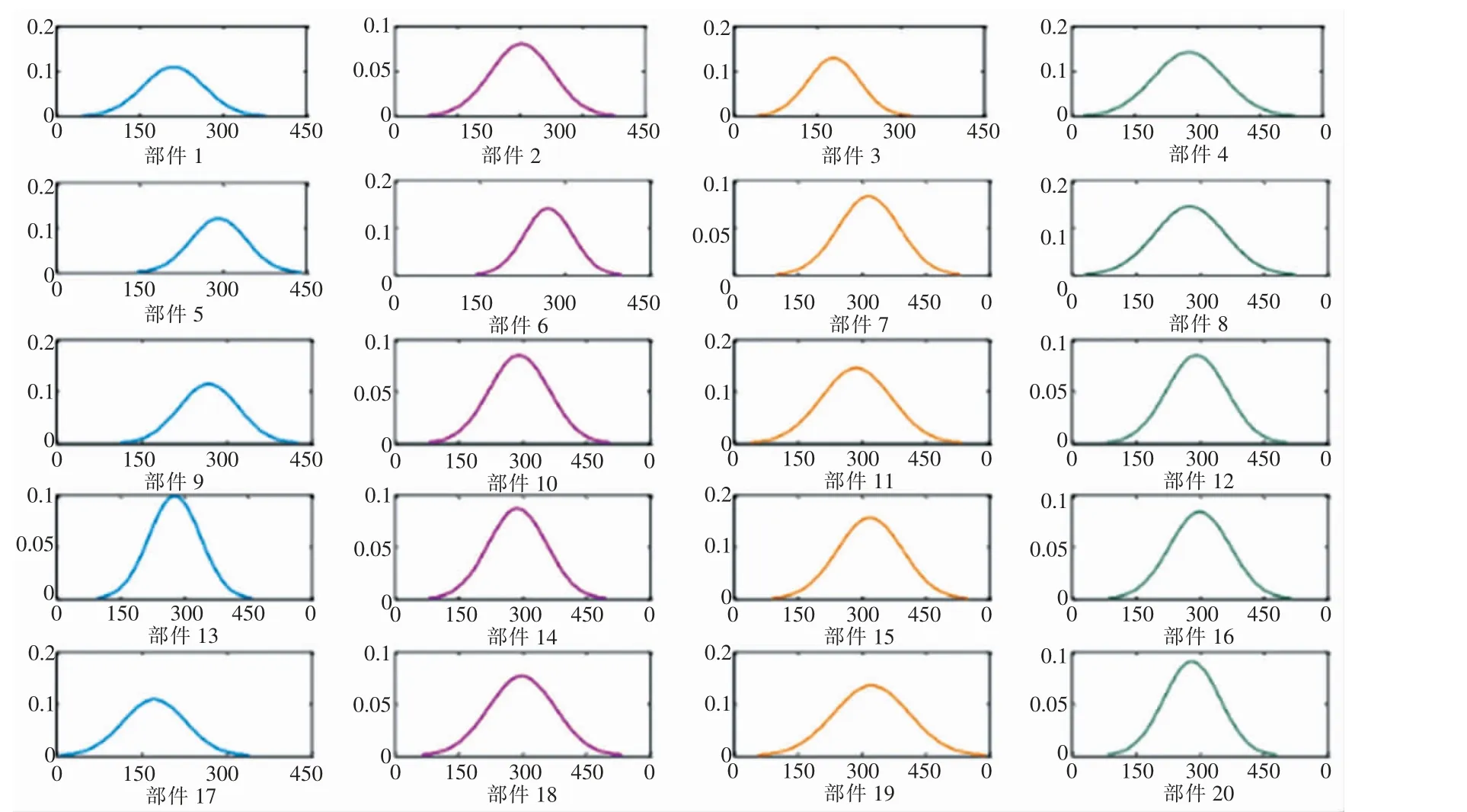
圖3 20 個部件剩余壽命Y 分布函數圖

采用聚類方法， 當得到相應的數據組類型后，讀取同一類型內的參考數據組的部件壽命，即檢測數據ω>0.7 的時間T。 將參考數據組的部件壽命T 與對應待求數據組作差，得到該類型部件在128 次檢測后的剩余壽命所呈現特征， 經過分析擬合，不同待求組所分類型得到的剩余壽命Y 均服從正態分布。

3 裝備存儲方案

本文通過假設，將裝備儲存方案變為一個線性規劃問題求解。 由部件剩余壽命分布函數，求得各部件在每一天的失效概率。將20 個部件的訂貨時間、更換時間作為變量，求解在約束條件下，使與其費用最低時， 變量的最優取值， 從而確定20 個部件的訂貨時間、每次訂購數量和部件更換時間，得到最優方案。

為了簡化問題，本文對實際情況做如下假設：

1） 各個部件每個只需要更換一次。

2） 每個部件有且僅有一個指定備件， 且備件相互之間不可混用。

3） 不到方案規定的更換時間， 即使部件失效且有備件，也不進行更換。

4） 費用最低指單位使用時間上費用最低。

本文將決策問題轉化為線性規劃問題。

記20 個部件的訂貨時間為TD1，TD2， …，TD20，20個部件的更換時間為TH1，TH2，…，TH20。 記進貨次數為n，每一次進貨數量為N1，N2，…，Nn。

由于部件購買價格固定，在前述的假設中已規定只購買20 個備件，這部分花費大小是固定的，可以不予以考慮。

記部件i 所花費的所有花費期望為fi， 在單位使用時間下，部件花費期望為。定義總費用ftotal為所有單位時間花費與訂貨費用之和的期望，有

將20 個部件的訂貨時間TD1，TD2，…，TD20以及更換時間TH1，TH2，…，TH20作為線性規劃的決策變量。 即決策變量共有40 個。

目標函數為

由于需要優化的參數多達40 個， 而且參數間相互影響，僅用普通的線性規劃方法難以得到優化結果并進行比較分析。為此，選用遺傳算法，以快速求解模型的近似最優解。

遺傳算法是一種采用生物進化理論進行選擇問題的近似最優解的方法。 它具有不要求函數連續、可擴展性、潛在的并行性等優點，已得到了廣泛的運用。它的實施過程包括編碼、產生初始種群、計算適應度、選擇、復制、交換、突變、反復迭代、終止等操作。

本文使用Matlab 自帶的遺傳算法庫函數ga（）進行求解。 設定種群大小為100，演化1000 代，染色體交叉的概率為0.8，染色體變異概率為0.05。在約束條件下，優化的目標函數，使得總費用期望值最低。對這些參數進行編碼并仿真，得到的結果（仿真求解的結果為小數，將其向下取整，取值為整數天數）如下：

訂購次數n=4 次， 分別在第974 天、1184 天、1401 天、1610 天進行訂貨。

4 維修策略

本文采用周期性視情檢測策略，即在離散時間點tk=kΔt（k∈N）進行檢測，Δt 為固定的檢測時間間隔，檢測后可獲得各個部件的實際退化量， 可根據F（t）計算得到各部件的剩余壽命Y。維修的首要目的是減少非計劃故障，因此，在tk，時刻進行檢測時，部件i的剩余壽命Yi必須大于檢測時間間隔Δt， 以用來避免下一個檢測間隔期內出現故障。同時，根據Yi的大小確定是否進行預防性更換，即在tk，時刻進行檢測時， 如部件i 的剩余壽命Yi小于預設的剩余壽命閾值tpr（tpr≥Δt）時，則進行預防性更換，所需要費用為Cpr；如部件在(tk-1，tk)期間發生了故障，則在tk時刻對其進行修復性更換，所需費用為Cf，(Cf>Cpr)，以上維修策略實施的前提條件是有備件可用。

（S，s）策略是目前比較通用的備件策略，即倉庫內能存放的最大備件數S， 當備件數下降到s 時，發出訂購S-s 個新備件的指令。假設備件單位時間的庫存持有成本為Ck，備件存放在倉庫里不會劣化。 每個備件購買的成本為Cpart，備件從發出訂購訂單到到達倉庫的時間間隔為交付時間t。 目前的(S，s)備件策略較為被動，只在備件被消耗到一定程度后才會發起訂購，由于購買的備件需要t，的時間才能到達，一些復雜關鍵部件的交付時間甚至長達數周，如果交付時間內， 多個同類型部件需要進行預防性或修復性維修，較低的安全庫存量很可能就無法應對。而維持較高的庫存則需要長期支付高昂的庫存費用。 為此，本文在維修決策與備件庫存量優化的基礎上，還采用了備件預約的概念， 即當部件的剩余壽命下降到一個閾值時，該部件可向庫房預約一個備件，此時該備件就被該部件鎖定。 除非有部件出現故障且無備件使用時，否則該備件僅供被預約的部件使用。相應的備件策略可優化為：若cs-bs≤s，則發出訂購備件訂單，其中cs為當前備件庫存量，bs為被預約的庫存量。

根據維修決策與備件庫存量聯合策略的分析可知，聯合優化的目標是在保證安全的條件（即Δt≤tpr）下，使得無限時間范圍內系統維修和備件總成本的平均費用率到達最低，需優化的參數有：剩余壽命閾值t，預約備件的時間閾值tpr和庫存參數S，s。 因此，優化模型可以描述為

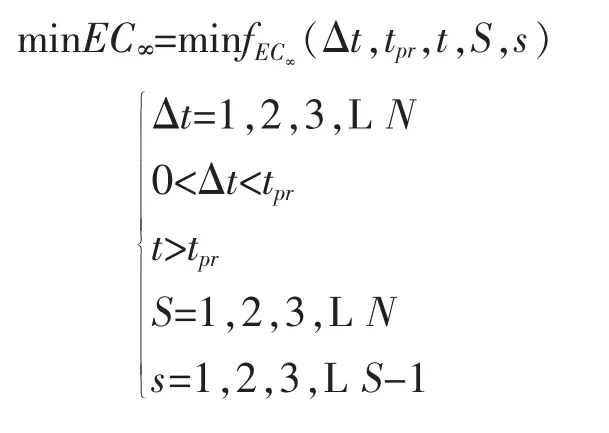
式中，fEC∞（Δt，tpr，t，S，s）為平均費用率函數。 由于需要優化的參數多，而且參數間相互影響，僅用蒙特卡羅方法難以得到優化結果并進行比較分析。 為此，選用遺傳算法和蒙特卡羅仿真相結合的方法，以快速求解模型的近似最優解，論文給出的聯合優化模型的求解流程如圖4、圖5 所示。

圖4 總體仿真流程

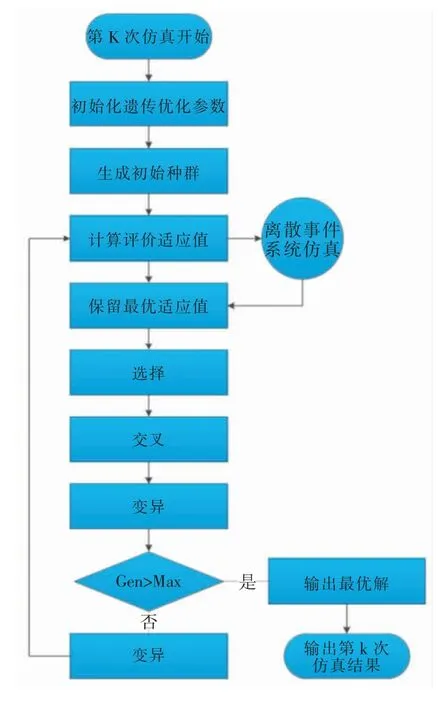
圖5 第K 次仿真流程

根據模型求解可得，得到長期最經濟且可信度較高的維修策略為：

達到1861 天后，統一更換60 個部件，以此類推，每過1861 天，即更換所有部件，在更換部件前60 天，即訂貨。 一輪正常更換所需費用20990 萬元，可以使用1861 天，部件可靠度為90%。

5 結 論

基層部隊裝備多，技術復雜，維修決策的內容多、難度大。采用裝備維修策略決策技術可以充分利用已有維修信息和故障知識，從而制定出科學的維修策略，為故障裝備的維修縮短時間，降低費用；為基層部隊制定科學的維修大綱提供依據。本文在國內外維修策略技術相關研究的基礎上，利用功能分析方法，建立了裝備維修策略決策的功能模型，劃分出了裝備維修策略決策的功能模塊。結合某裝備中的維修策略的具體實現，以裝備故障模式、影響分析和故障分布模型分析為決策的基礎，研究了裝備維修方式和（S，s）、維修級別及維修次序的決策，較好地實現了裝備維修方式、維修間隔期、維修次序、維修級別的決策，并取得了初步應用效果。