無窮限反常積分的狄利克雷(Dirichlet)判別法的應用探討
李 霞
(沈陽理工大學理學院,遼寧 沈陽 110159)
無窮限反常積分是定積分的一種推廣形式,其收斂性的判別在基礎數學理論體系與其他學科實際應用中都有著重要的意義.在諸多收斂性判別法中,狄利克雷(Dirichlet)判別法則是理論意義重要但實際操作難以下手的一個定理.因此,能否找到一類適合狄利克雷判別法條件要求的被積函數,成為解決問題的關鍵,本文通過實例進行類推,以期對狄利克雷判別法的實際應用有所促進.
定理[1]設f(x),g(x)在[a, +∞)上有定義,
(1) ?X>a,g(x)∈R[a,X],?M> 0,使得對
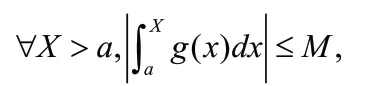
(2)f(x)在[a, +∞]上單調,且
由定理,狄利克雷判別法將函數乘積的無窮積分的收斂性判定問題轉化為判定兩個函數是否滿足特定條件的形式. 但在具體應用中,相對于判別部分因式是否單調趨于零,更為困難的則是尋找是否有部分因式作為被積函數時積分有界.
先討論可以應用狄利克雷判別法的例子.
解 : 對g(x)=cosx,?M=2,對于?X> 1,
由狄利克雷判別法,當α> 0時,收斂.
從例1發現,當取g(x)為三角函數時,可以很輕松地得到其積分有界的結論,從而直接應用狄利克雷判別法求證,在某種程度上,是三角函數的周期性及函數值有規律的取值使其很好地滿足了判別法的條件,那么三角函數的特性能否化為更一般的規律呢?
例2:g(x)是(?∞,+∞)上周期為2π的連續函數,
證明:對?α> 0,收斂[1].
證明:顯然,對?X> 1,g(x)在[1 ,X]上連續且可積,故g(x)在[1 ,X]上有最值.
既 ?m,M∈R,m<M,當x∈ [ 1 ,X]時,m≤g(x)≤M成立.
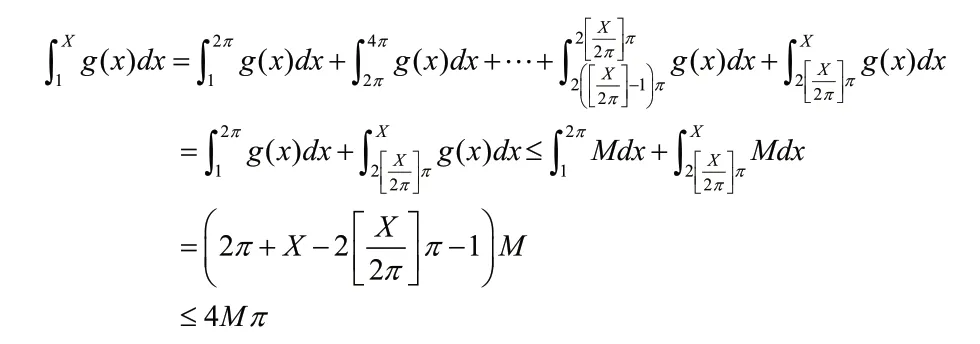
由狄利克雷判別法,對?α> 0,收斂.
例2提取了三角函數一個周期內積分為零這一特性,構成了更為一般的條件.進一步,條件“g(x)是(?∞,+∞)上周期為2π的連續函數,可弱化為“g(x)是(?∞,+∞)上周期為T的連續函數,其中T為實數,T> 0”。
這樣就找到了更具普適性的一類函數,可以通過證明其積分有界,從而利用狄利克雷判別法證明其與某單調趨于零函數的乘積的廣義積分收斂.但是,這也僅僅窺得問題答案的冰山一角,相信經過深入的理論研究,可以有更多發現.

