關(guān)于加速度絕對性的研究

馮張彬

（沈陽化工大學(xué)，遼寧 沈陽 110142）

眾所周知速度是相對的，如果粒子A相對于粒子B以速度→運(yùn)動，則粒子B相對于粒子A以速度運(yùn)動. 但是如果把速度換成加速度，以上相對性還成立嗎？如果粒子A相對于粒子B的加速度是，則粒子B相對于粒子A的加速度是嗎？根據(jù)經(jīng)驗(yàn)不難猜想A測得B的加速度與B測得A的加速度方向是相反的，但是它們的大小相等嗎？本文從運(yùn)動學(xué)角度對此作一分析.

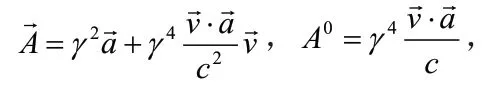
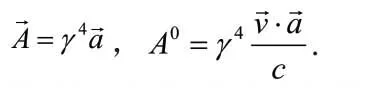
這是以粒子B所處的參考系測得的粒子A的四加速度，如果以粒子A所處的參考系來測量A的四加速度，只需令上式=0即可，這時(shí)γ=1，粒子A的四加速度為

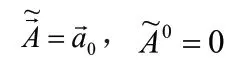
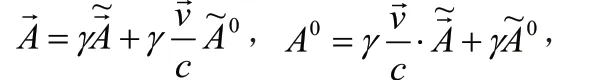
下面再以A為參考系測量B的加速度，由于A具有加速度，所以A所處的參考系是非慣性系，所以不能用閔氏度規(guī)來描述這個(gè)參考系了，取而代之的是Rindler度規(guī)，這里以粒子A的固有時(shí)t作為這個(gè)坐標(biāo)系的坐標(biāo)時(shí)，A的運(yùn)動方向設(shè)為x軸方向，只考慮x與t這兩個(gè)坐標(biāo)，則Rindler度規(guī)為：

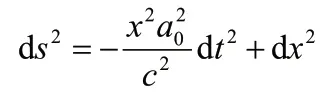
其中a0仍然是粒子A的瞬時(shí)靜止加速度，定義，則上式成為：

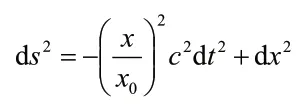
可以看出粒子A在x軸的坐標(biāo)為x0. 根據(jù)Rindler度規(guī)，可以計(jì)算出它的克氏符：

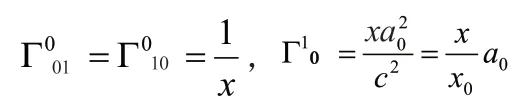
因?yàn)榱Ｗ覤處于慣性系中，不受任何的力，所以在Rindler時(shí)空中粒子B沿測地線運(yùn)動，可以用B的固有時(shí)τ為參數(shù)列出B在Rindler坐標(biāo)系下的測地線方程：

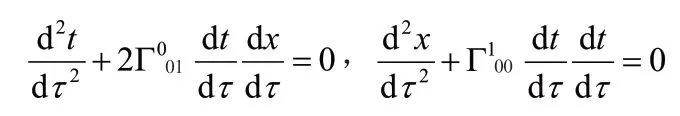
其中，t與x分別是粒子B在這個(gè)坐標(biāo)系的時(shí)間與空間坐標(biāo)，聯(lián)立這兩個(gè)方程，消去τ解得：

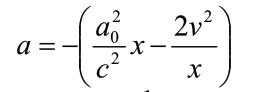
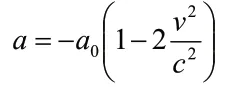
可以看出即便A、B兩粒子的空間位置相同，它們相互測得的加速度雖然方向相反但大小并不相等. B測得A的加速度大小是而A測得B的加速度大小是當(dāng)然在低速條件下，粒子A的運(yùn)動速度遠(yuǎn)小于光速即v＜＜c時(shí)，v/c這一項(xiàng)可忽略，那么B測得A的加速度與A測得B的加速度確實(shí)是大小相等方向相反的，這與我們?nèi)粘Ｉ罱?jīng)驗(yàn)相符.

下面我們再對這個(gè)結(jié)果作一物理上的說明. 首先粒子B觀測粒子A的加速度大小是我們知道速度疊加公式：

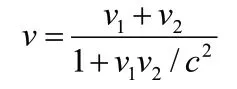
例如粒子A以速度v相對于B運(yùn)動，一段時(shí)間以后以A為參考系發(fā)現(xiàn)它的速度增加了dv，則以B為參考系發(fā)現(xiàn)它的速度增加了

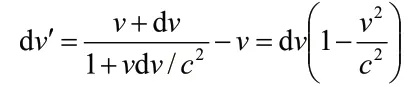
也就是說以A為參考系發(fā)現(xiàn)它的速度增加了dv，則以粒子B為參考系發(fā)現(xiàn)A的速度增加了下面我們再考慮時(shí)間膨脹效應(yīng)，設(shè)粒子A的速度增加了dv（以A為參考系的測量值）所用的時(shí)間是dt，而以粒子B為參考系發(fā)現(xiàn)這一過程所用的時(shí)間是

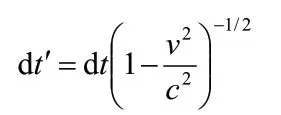
這樣，以B為參考系測得的A的加速度為

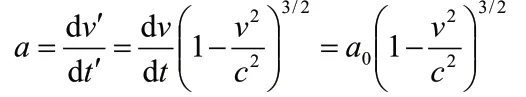
通過上面的分析可以看到，在狹義相對論的框架內(nèi)，加速度的相對性并不成立，即A相對于B的加速度與B相對于A的加速度并不是大小相等方向相反的，這是加速度與速度之間的不同. 實(shí)際上我們可以說速度是相對的，而加速度是絕對的. 產(chǎn)生以上不對稱性的原因是粒子B處于慣性系中，而粒子A有加速度處于非慣性系中. 所以加速度的不對等性可以看作是慣性運(yùn)動與非慣性運(yùn)動之間的不對等性. 所謂慣性運(yùn)動與非慣性運(yùn)動是指當(dāng)且僅當(dāng)質(zhì)點(diǎn)的世界線是類時(shí)測地線時(shí)，質(zhì)點(diǎn)的運(yùn)動稱為慣性運(yùn)動；反之則為非慣性運(yùn)動．