基于數值模擬的巷道交叉口支護參數優化研究

王建貴，楊八九，者亞雷

(1.云南錫業股份有限公司， 云南 紅河州 661000；2.云南亞融礦業科技有限公司， 云南 昆明 650000)

0 引言

巷道開挖后，破壞了圍巖的原巖應力平衡，引起新的應力分布，巷道圍巖的應力狀態由原來的三向應力狀態改變為二向應力狀態，水平應力向拱頂巖層轉移，垂直應力向兩幫轉移，拱頂以下巖層主要受水平應力作用，容易失穩破壞[1-2]。當交叉口處第二條巷道掘進時，會再次引起圍巖應力的重新分布，造成支承壓力的相互疊加，拱頂巖層承受的水平應力會進一步增大。雖然第一條巷道掘進時的錨桿可以控制水平應力作用下頂板巖層的剪切破壞，但在對交叉口處巷道進行施工時，頂板上位巖層會產生新的松動離層破壞區，使得頂板巖層潛在冒落危險。研究表明，交叉口處第二條巷道掘進后，應力集中系數比開掘前增大40%～50%[3-4]。因此交叉口處巷道的支護參數優化研究具有重要意義。

1 工程概況

本次研究對象為大屯錫礦高峰山礦段無軌巷道交叉口，巷道為三心拱斷面，單一斷面大小為4.5 m×4.3 m，交叉口位置開挖后頂板最大暴露面積約為93.72 m2（圖1中畫斜線區域）。巷道位于大理巖層中，通過室內試驗得到巖塊力學參數后采用Hoek-Brown強度準則折減確定高峰山礦段大理巖巖體黏聚力c=0.3219 MPa，內摩擦角φ=37.69°，抗拉強度τ=0.3164 MPa，彈性模量G=9.0794 GPa。容重為γ=27.2 kN/m3。巷道距地表的埋深H=1000 m，交叉口處巷道相關尺寸見圖1。

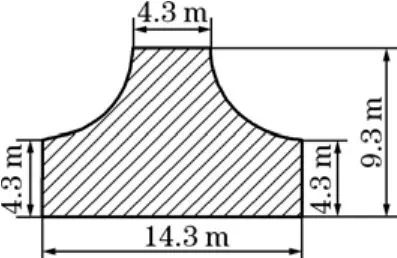
圖1 大屯錫礦巷道交叉口相關尺寸示意

2 錨索長度計算

錨索長度L由下式確定：

式中，L1為錨索內錨固段長度，m；L2為錨索自由伸段長度，m；L3為錨索張拉段長度，m。

錨索的錨固段長度L1按照錨索與水泥藥卷粘接強度相匹配原則確定：

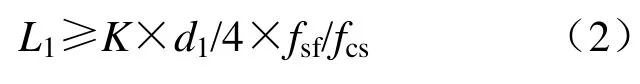
式中，d1為錨索直徑，mm；fsf為錨索的抗拉強度，查得2246.5 N/mm2；fcs為樹脂藥卷與錨索的粘接強度，10 N/mm2。K為安全系數，取1.2。

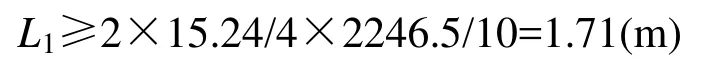
錨索自由伸長段L2由不穩定圍巖的松動范圍來確定：

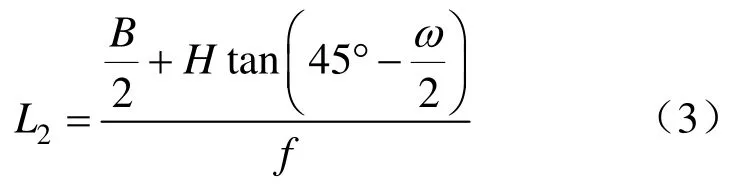
式中，B為巷道掘寬，按巷道交叉口處最大跨度計算，13.7 m；H為巷道掘高，m；f為頂板巖石普氏系數；ω為兩幫圍巖的似內摩擦角，°。

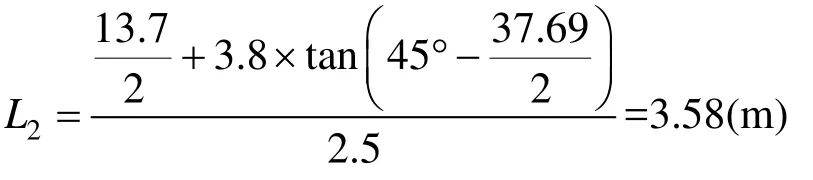
錨索外錨段長度L3應滿足安設錨具的張拉需要，取L3=0.3 m。

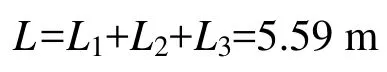
3 模型的構建

根據彈塑性力學理論可知，在承受均勻載荷的無限大彈性體中開挖圓孔后，孔邊的應力狀況會發生明顯變化：在3倍孔徑的區域，應力較原始狀態增加11%；在5倍孔徑的區域，應力的相對差值已小于5%，這樣的應力變化在工程上可以忽略不計。因此，在計算中可以把 3～5倍孔徑的區域作為計算域。為了滿足計算需要和保證計算精度，本次計算采用的模型尺寸為巷道尺寸的5倍。X方向長度為200 m，Y方向長度150 m，Z方向長度為104.15 m。建好的計算模型如圖2所示。

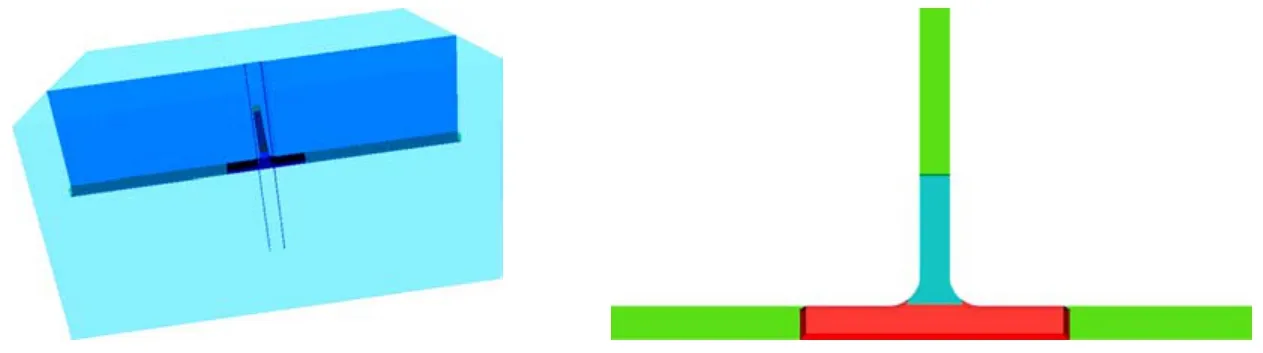
圖2 巷道交叉口模型

由于采動影響范圍有限，在離巷道較遠處的巖體位移值將很小，可將計算模型邊界處位移視為零。因此，計算域邊界采取位移約束，即模型底部所有節點采用x、y、z三個方向約束，模型x方向的兩端采用x方向約束，模型y方向的兩端采用y方向約束。巷道埋深按1000 m計算，模型頂部圍巖為大理巖，施加27.2 MPa的力模擬上覆巖層自重。

4 計算方案

結合現場實際制定的計算方案見表 1，錨索長度在理論計算值5.59 m的基礎上適當加長。

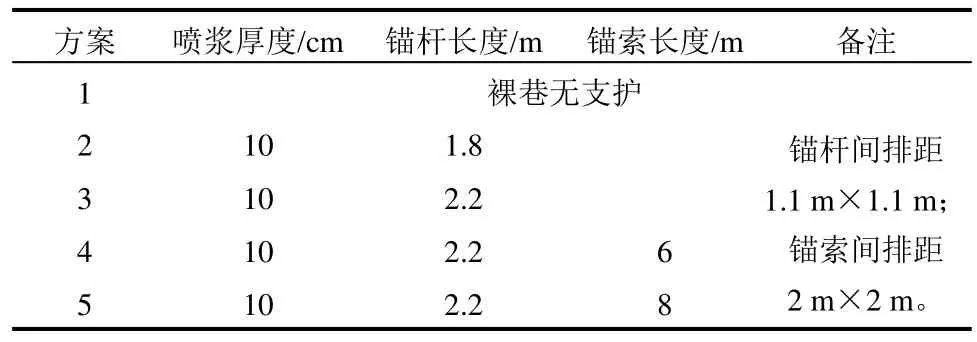
表1 計算方案

5 計算結果分析

5.1 無支護時巷道穩定性分析

從圖3、圖4可以看出，交叉口處巷道開挖后，巷道圍巖有一定的移動變形，位移量最大的區域發生在兩條巷道交叉口拱頂及邊壁位置，最大位移量為 10.9 cm。巷道開挖后裸巷圍巖出現了大范圍的塑性區，且塑性區整體連片，說明此時巷道處于不穩定狀態，會發生垮塌或失穩破壞。

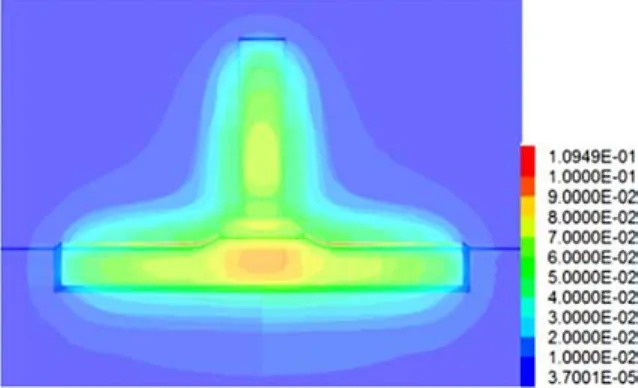
圖3 方案一：不支護整體位移

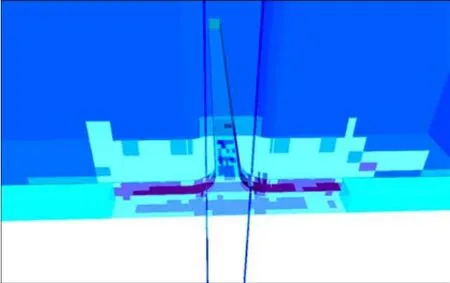
圖4 方案二:不支護整體塑性區

5.2 支護巷道穩定性分析

5.2.1 整體位移

巷道開挖后采用噴錨支護，其中方案四、方案五（見圖5）采用錨桿+錨索支護方式，在巷道開口處增加6 m、8 m長錨索進行加固支護。

從圖5可以看出，與不采用支護手段相比，錨桿支護后圍巖位移從10.9 cm減小到9.23 cm、9.04 cm，效果不是特別明顯，而增加錨索加固后兩方案的圍巖位移從10.9 cm減小到6.15 cm、5.72 cm，比不支護時減小了近一半，效果較好。

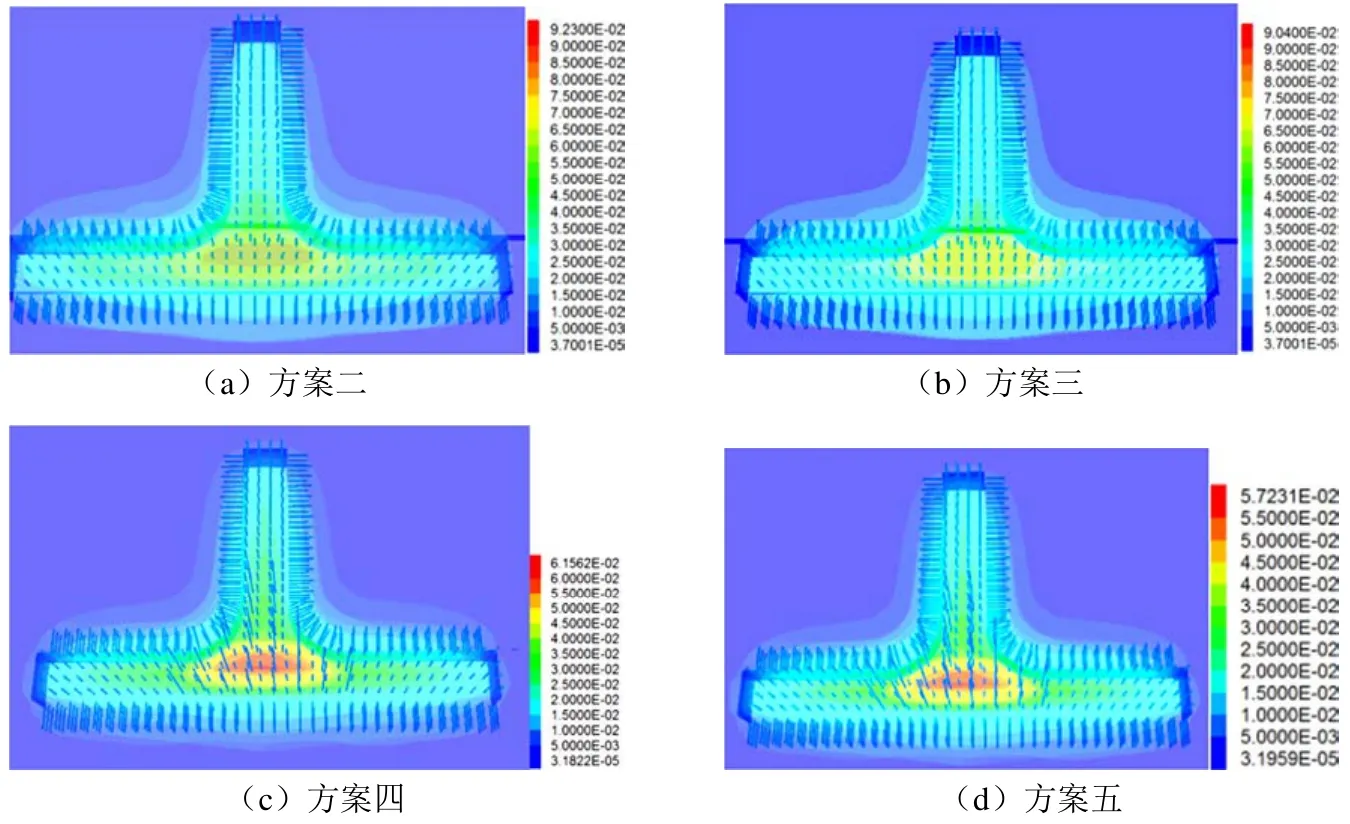
圖5 不同支護方案的巷道圍巖位移

5.2.2 錨桿、錨索受力分析

由于方案較多，以下選取不采用錨索支護的方案三和錨索加固后的方案四進行錨桿、錨索的受力分析。

從圖6可以看出，受力最大的錨桿、錨索均在巷道交叉口處，交叉口處錨桿所承受的載荷相應地比其它部位高0.5倍左右。不打錨索時，交叉口錨桿受力最大值為99.71 kN，而現場測試的錨桿拉拔力僅為50 kN左右，此時錨桿受力已遠超其自身的拉拔力值，處于失效狀態；采用錨索加固后交叉口受力最大值由錨桿轉移到錨索上，達到153 kN，此時錨桿的受力明顯減小，說明錨索發揮了極其重要的作用，能夠較好的控制頂板地壓，減小錨桿受力，使整體支護達到較好的效果。

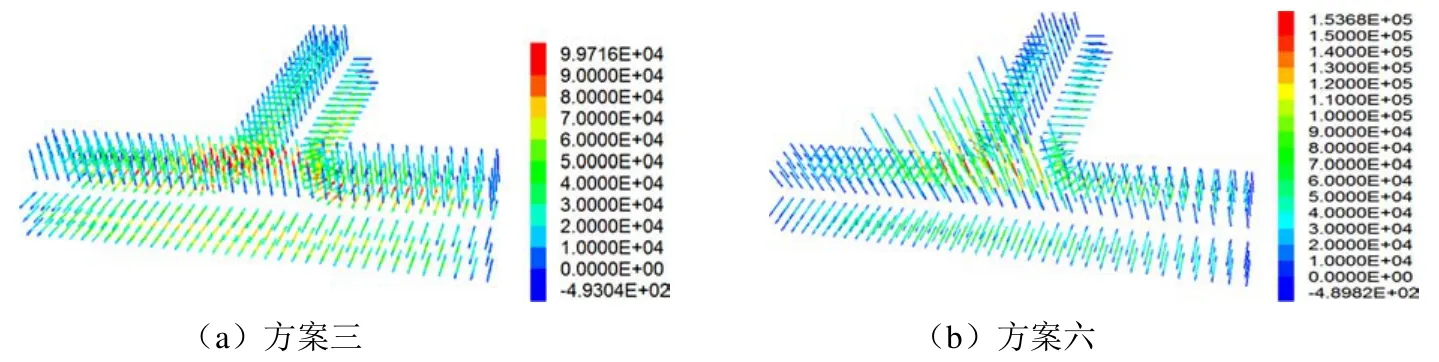
圖6 各方案錨桿、錨索受力

5.2.3 塑性區分析

由于方案較多，僅對選取不采用錨索支護的方案三和錨索加固后的方案四進行塑性區分布的比較。

從圖7可以看出，交叉口處巷道整體采用錨桿支護后，巷道圍巖塑性區與不支護相比有所減少，巷道開口處仍存在塑性區連片的現象。而拱頂采用錨索加固支護后，開口處的塑性區較錨桿加固方案明顯減少，并且塑性區都是獨立存在，沒有明顯連片現象。這是由于巷道交叉口處的潛在冒落區范圍較大，普通的錨桿（長度在2.4 m以下）不能伸入到冒落區以外，只能加固潛在冒落區內的巖層，所以為了防止頂板上位巖層的大面積冒落，需要在交叉口處布置錨索，穿過潛在冒落區伸入到頂板深部穩定的巖層中。因此，在巷道開口處打長錨索進行加固支護有利于巷道圍巖整體穩定。

6 結論

（1）采用FLAC3D數值模擬軟件對大屯錫礦巷道交叉口支護方案進行模擬分析，認為采用錨索加固能較好的控制圍巖變形，支護后圍巖位移量僅為錨桿支護時的63%，效果顯著。

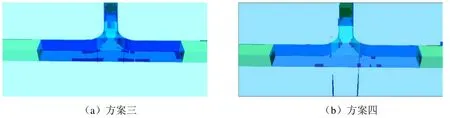
圖7 錨桿支護與錨索加固后塑性區分布

（2）采用錨索加固后交叉口最大受力值轉移到錨索上，達到153 kN，此時錨桿區域的受力明顯減小，說明錨索發揮的作用明顯，能夠較好的控制頂板地壓，減小錨桿受力，使群體支護達到良好的效果。

（3）由于巷道交叉口處的潛在冒落區高度較大，普通的錨桿（長度在2.4 m以下）不能伸入到冒落區以外，為防止頂板上位巖層的大面積冒落，在交叉口處布置錨索，穿過潛在冒落區伸入到頂板深部穩定的巖層中有利于巷道圍巖的穩定。

（4）通過綜合分析，結合錨索長度的理論計算，認為錨桿長度為2.2 m，錨索長度為6 m，錨桿間排距為1.1 m×1.1 m，錨索間排距為2 m×2 m的聯合支護方案是經濟合理的可行支護方案。

（5）研究成果為大屯錫礦巷道交叉口的支護提供了理論依據，研究結果具有一定的參考價值。