錨桿錨固質量應力波檢測的固結波速探索

鄭軍

(攀枝花市興茂動力設備安裝有限公司， 四川 攀枝花市 617000)

0 引言

錨桿錨固質量的判別是評估井巷圍巖控制效果的一項重要內容[1]。當前，對錨固質量的判斷主要有兩類方法[2]：一是基于錨桿拉力儀的拉拔性檢測，該方法雖可靠度較高，但屬于破壞性抽檢，實施過程中會降低錨桿對巖體的錨固作用[3]；二是基于應力波測試的無損檢測，其原理是向錨固系統注入沖擊性擾動，通過檢測系統的振動信號，識別有關振動參數，并以此作為反映系統錨固質量的表征，此方法具有實時、高效的優點，是一種無損傷的間接測試法[4]。相關研究提出了諸多用于表征錨固質量的參數，包括振幅比、波阻抗、信號相速率、能量速率、衰減系數等[5]。其中，固結波速是一個廣泛被大家認可的參數，其物理含義是激發應力波在錨固段內的傳播速度[6]。固結波速會隨錨固強度的不同而發生變化[7]，當錨固質量較好時，意味著固結強度較高，固結波速將趨近圍巖體的波速；當錨固質量較差時，意味著錨桿桿體與錨固劑或錨固劑與圍巖之間的粘結強度不足，固結波速會趨近于錨桿桿體的波速。因此，固結波速便成為能綜合體現錨固優劣的指標[8]。但是，現實中通過分析應力波檢測信號來獲得固結波速往往會遇到難以克服的困難，原因是確定固結波速的錨桿底端反射難以被識別[9]。由于錨固段內應力波能量的散射以及固端界面應力波的多次反射，特別是錨固質量越好時行波的能量散射愈明顯，導致到達底端的應力波大大減少，底端反射信號非常微弱[10]。因此，需要另辟蹊徑，破除僅僅依靠識別底端反射來確定固結波速的思維困局，尋找其他能確定固結波速的易識別振動參數。為此，本文利用波動理論，建立錨固系統振動力學模型，探索固結波速與易識別振動參數的關系，為固結波速的求解提供參考。

1 錨固系統振動力學模型

激振力作用下端錨錨固系統如圖1所示。f為激振力錘施加于錨桿外端的振源沖擊力，kN，因其引起的錨固系統振動信號由加速度傳感器采集；l1和l2分別為錨桿自由段與錨固段長度，m；d1與d2分別表示錨桿自由段和錨固段直徑，mm；ρ1為錨桿桿體材料密度，ρ2為樹脂錨固劑密度，kg/m3。假設從錨桿外露端起建立X坐標軸，則錨固系統任意截面位置x處的振動位移為u，u是與x和振動時間t有關的物理量。

對于錨桿自由段（x∈[0,l1]），其振動位移u1(x,t)滿足波動方程：

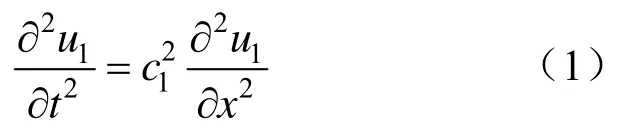
式中，c1為應力波在自由段內的傳播速度，m/s；=E1/ρ1，E1為錨桿桿體彈性模量，GPa。

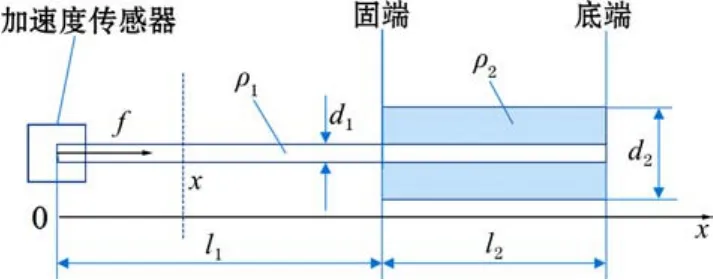
圖1 受激振力作用的錨固系統

利用分離變量法對式（1）求解得：

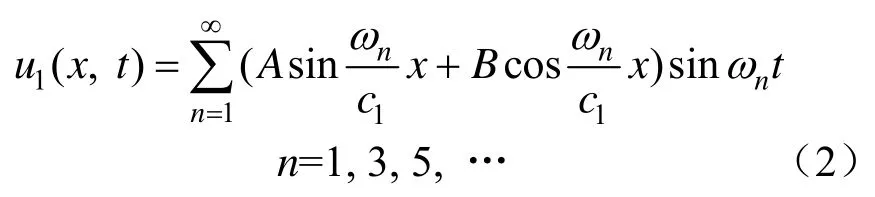
其中，ωn為振動固有頻率，Hz；A、B為待定系數，由邊界條件確定。

由于自由段可等效成是一端受載，一端有集中質量（錨固段）的桿件模型，則其固有頻率ωn=同時為研究方便，取振動基頻，即n=1時，另外，規定振動時間t為應力波單程行波時間，即t∈ [ 0,l1/c1]。

當t=0時，在x=0的邊界上，根據沖量定理，有：

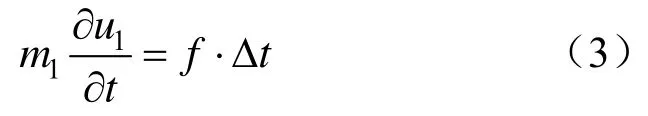
在x=l1的邊界上，根據牛頓定理，有：

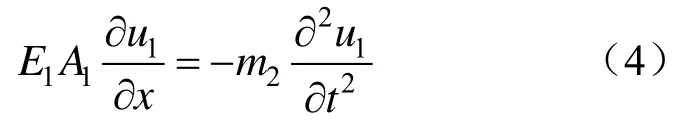
式中，m1和m2分別為自由段與錨固段質量，kg；Δt為沖擊荷載作用時間，一般取1/1000～1/10 000 s；A1為錨桿桿體斷面面積，m2。聯合式（3）、式（4）解得待定系數：

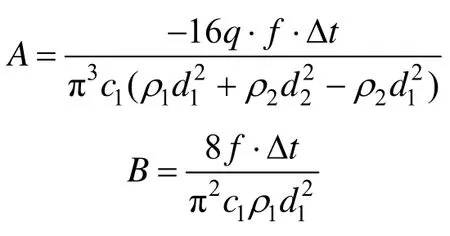
其中q=l1/l2。

同理，對于錨桿錨固段（x∈[l1,l1+l2]），其振動位移u2(x,t)也滿足波動方程，解的形式為：

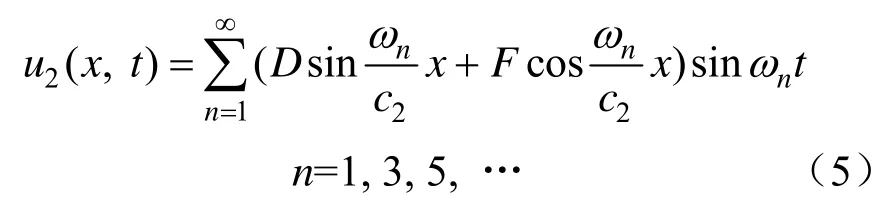
式中，c2為固結波速，m/s；D、F為待定系數。

因為錨固段可等效成固端自由、底端固定的桿件，所以其振動基頻ω= π ·c2/ 2l2。應力波在錨固段內單行傳播時間t∈[l1/c1,l1/c1+l2/c2]。

當t=l1/c1時，在x=l1的邊界上，有：

在x=l1+l2的邊界上，有：

聯合式（6）、式（7）解得待定系數：

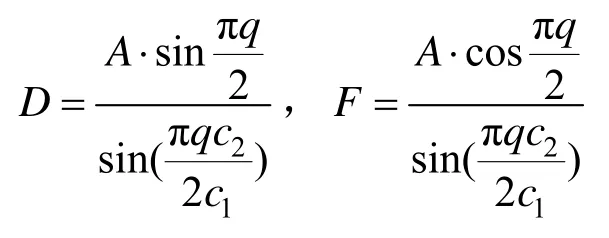
下面結合算例對振動模型進行說明。算例：一端錨錨桿長2.5 m，錨固段長0.5 m，鋼筋桿體密度7900 kg/m3，桿體直徑20 mm，樹脂錨固劑密度1500 kg/m3，錨固段直徑30 mm，桿體外端施加1個3 kN的激振荷載，荷載作用時間10-3s，假設應力波在自由段和錨固段的波速分別為 5000 m/s和3300 m/s。將上述參數代入式（2）和式（5）中得到行波單程時錨固系統振動位移規律，如圖2所示。

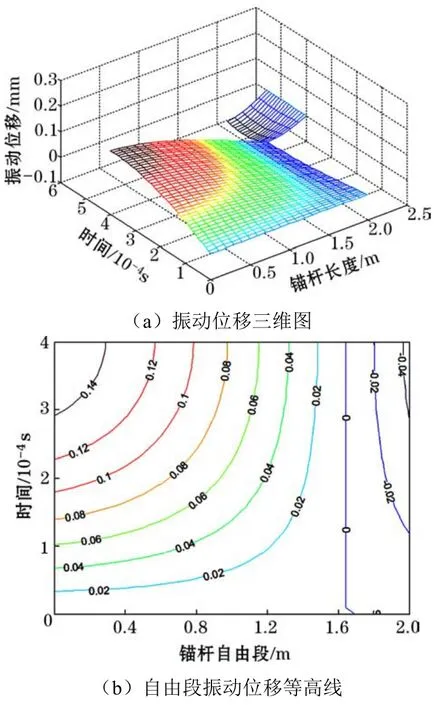
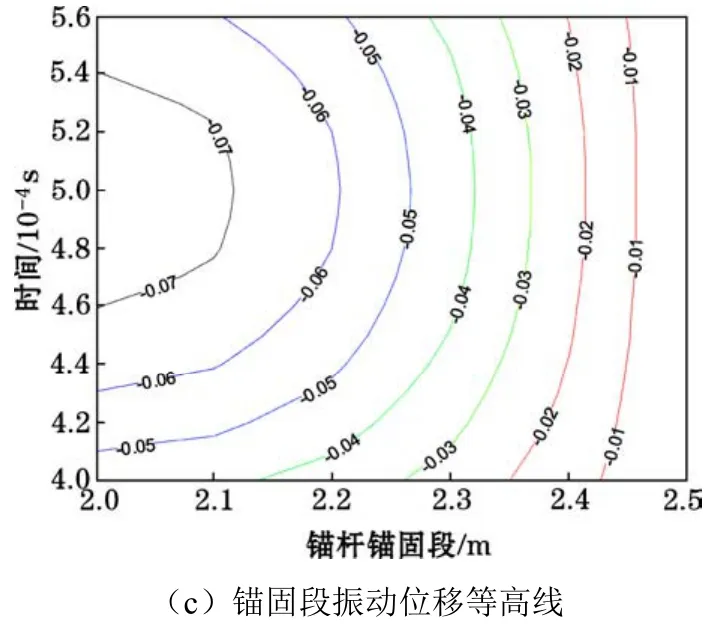
圖2 錨固系統振動位移分布

由圖2可知，對于自由段，從空間維度上看，振動位移沿錨桿從外向內逐漸減小；從時間維度上看，振動位移隨時間延長而增大，但距振源的位置越遠，位移增幅越小。說明自由段內不同截面位置介質的振動幅度不等、振動分布不均勻，體現了振動能量在時空上的不均衡傳遞。顯然，最外端截面的振動位移最大，且時間效應也最顯著，而在應力波沿桿體傳播的過程中，振動的時空效應均出現減弱，這與聲波檢測信號呈現的振幅逐漸衰減規律一致。另外，位移在桿體1.68 m處為0，且該位置前后位移出現反向，表明受應力波擾動作用，0 m～1.68 m的桿體段與1.68 m～2.0 m的桿體段內介質分別呈受壓和受拉狀態，桿體內應力波為縱波，體現了縱波傳播的疏（拉）密（壓）特征。

對于錨固段，從空間維度上看，振動位移在固端界面最大，在底端界面為零，在兩界面之間逐漸減小；從時間維度上看，振動位移隨時間延長先增大后減小，呈“倒鐘形”規律分布，“鐘頂”所對應的時刻為固結波（錨固段內傳播的應力波）傳播耗時的一半。整體看，錨固段振動位移在時空上的分布較為規律、變化均勻。特別是固端振動明顯、底端振動微弱，這一現象與現實聲波檢測信號呈現的固端反射清晰、底端反射難于識別的規律相一致，為底端反射識別困難提供了充分的理論解釋。說明利用聲波檢測的固端反射信號易于識別的特點，通過理論模型建立固端振動位移與固結波速這兩個物理參數間的關系，可準確容易地獲得固結波速，避開了必須通過識別底端反射信號來獲取固結波速的技術難題。

2 影響固結波速與固端振動的因素

為弄清錨固參數對固結波速與固端振動位移的影響程度，采用正交試驗法對這些因素的影響力進行分析。試驗因素包括錨桿自由段長度、錨固長度、錨桿直徑、錨固段直徑以及錨固劑密度，各因素選擇5個水平，見表1。試驗方案及結果見表2。試驗結果選擇固結端最大振動位移，其值是將各方案參數代入式（5）計算而得。式（5）所需的其余參數同上節算例。結果顯示，錨固段長度這一因素的極差最大，說明其對固結波速及固端振動的影響最明顯，是主控因素。

圖3反映了不同錨固長度下固端最大振動位移與固結波速的變化規律。可以看出，因為錨固段介質質點的振動本質上服從正弦函數規律，錨固段長度作為正弦函數的一個參數，其變化改變著函數的相位，故當錨固段長度不同時，固結波速與固端最大振動位移的關系曲線均不相同。例如，同為2.5 m長的兩根錨桿，一根錨固長度為 0.4 m，另一根錨固長度為 0.5 m，其余錨固參數相同，若測得這兩根錨桿的固端最大振動位移均為-0.1 mm，則兩者對應的固結波速分別為3600 m/s和4840 m/s，代表著兩種不同的錨固質量。圖3還顯示出在表征錨固質量由好到差的固結波速所涵蓋的3000 m/s～5000 m/s的區間內，固端最大振動位移落在-1.5 mm～1.5 mm的范圍，而其中大部分位移值又分布在-0.02 mm～0.02 mm這個范圍內，在此范圍內，位移隨波速增加而緩慢增大（或減小）；在此范圍外，位移隨波速增加則加速增大（或減小）。這些位移驟變范圍所對應的固結波速區間因錨固段長度的不同而各異，如：錨固段為0.3 m、0.4 m、0.5 m、0.6 m、0.7 m時，固結波速區間分別為3800 m/s～4400 m/s、3600 m/s～4000 m/s、4600 m/s～5000 m/s、3000 m/s～3400 m/s以及 3600 m/s～4200 m/s。由此說明這些波速值往往對應著振幅明顯的固端振動，傳感器采集到的固端反射信號會較強，易于識別。另外，上述的固結波速區間內還存在一個值，它會使振動位移發生突躍，不過突躍點兩側曲線呈單調變化，表明不會有一個振動位移對應多個固結波速的情形出現，體現了由振動位移標定固結波速的準確性。

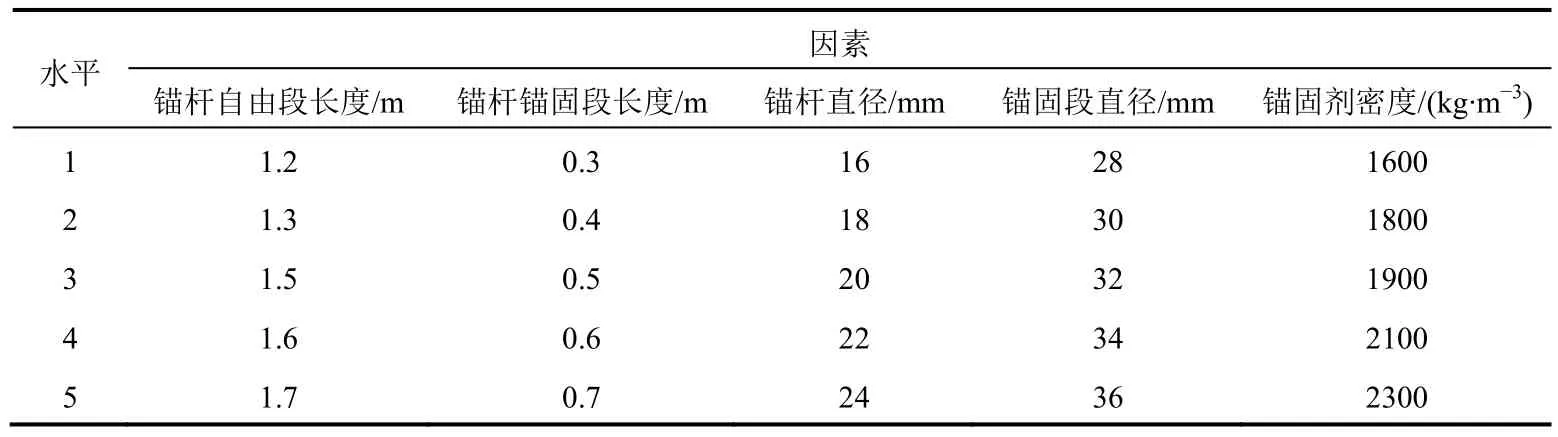
表1 試驗因素及其水平

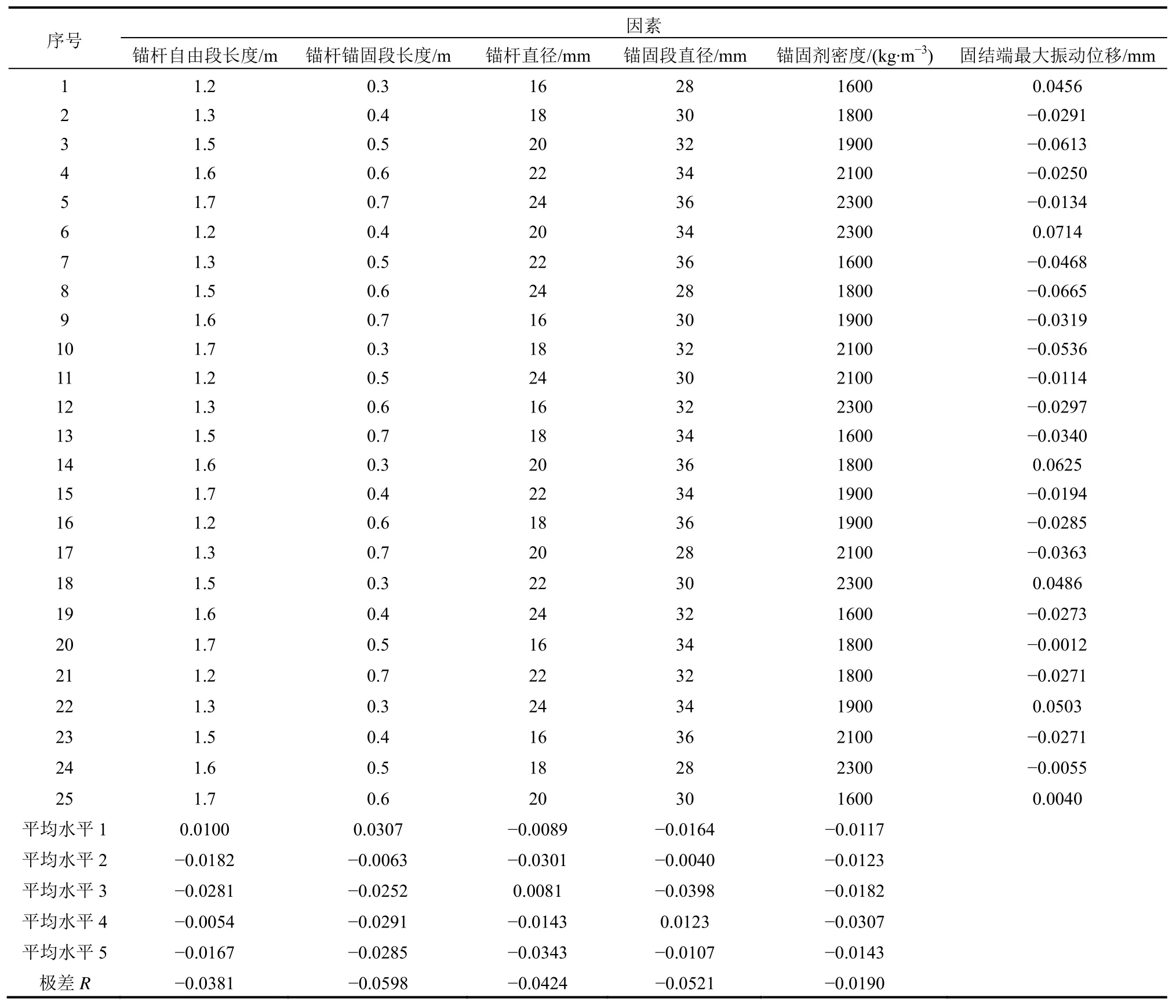
表2 試驗方案與結果

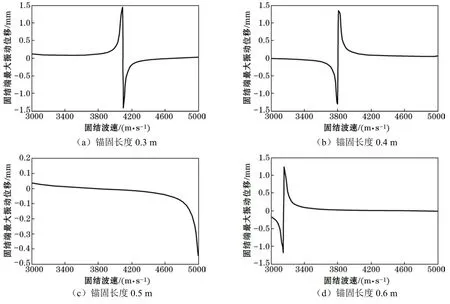
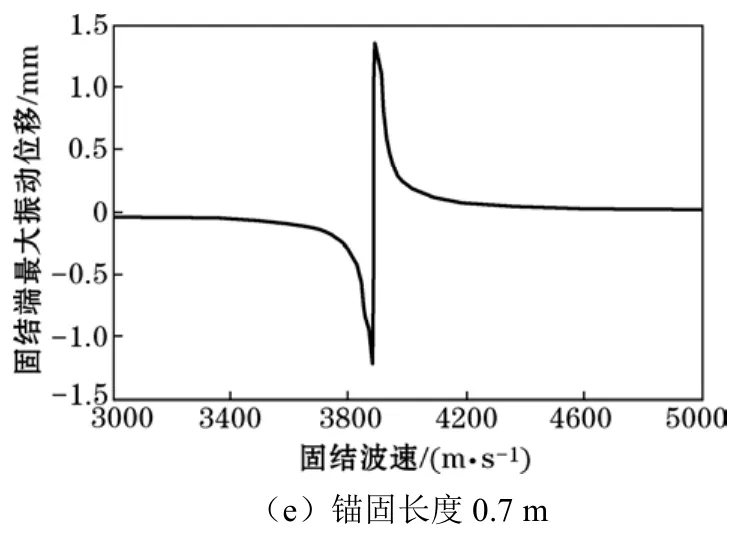
圖3 固結波速與最大振動位移的關系曲線

3 結論

（1）分別對端錨錨固系統的自由段和錨固段建立力學模型，獲得激振力作用下錨固系統的振動響應。在錨固段上，固端界面振動最大，底端界面無振動，振動從固端到底端逐漸減弱，并在時空上呈“倒鐘形”規律分布。

（2）建立固結波速與固端最大振動位移間的函數關系，分析相關錨固參數對該函數關系的影響程度，得到錨固長度為其主控因素的結論。分析得出不同錨固長度下，固結波速與固端振動峰值的變化規律。