落煤角與接觸角對煤巖與尾梁動態響應的影響分析

山東科技大學機械電子工程學院 山東青島 266590

煤 炭是我國的主要能源之一，在已探明的化石資源中所占的比例最高，在國民生產生活以及社會發展過程中必不可少。綜采放頂煤工藝具有成本低、環境適應能力強、集中生產與管理方便的優勢，是許多厚煤層及特厚煤層煤礦開采的主要方式[1]。綜采放頂煤過程中經常遇到大量煤炭垮落帶來的沖擊載荷[2]，沖擊產生之后，會使液壓支架的工作狀態與運動方式發生變化，沖擊嚴重時甚至會導致尾梁產生沖擊變形，進而影響煤炭開采的正常進行[3]。

目前國內外對于煤巖顆粒沖擊尾梁帶來相應變化的研究較少。梁利闖等人[4]對沖擊載荷作用下的液壓支架力傳遞特性作了分析，得出了沖擊載荷的位置不同，各鉸接點處受到的力也不同、力的傳遞特性不同的結論。趙忠輝等人[5]對液壓支架立柱在沖擊載荷作用下作了有限元分析，通過分析立柱的應力場分布，得出了立柱缸體的抗沖擊性能，及立柱在沖擊試驗過程中對地基等基礎設施的最大沖擊載荷。萬麗榮等人[6]研究了沖擊載荷作用于支架掩護梁后支架的運動及受力情況，提出了沖擊載荷作用位置不同，支架的動力學變化趨勢不同。

以上研究主要是以在液壓支架上施加沖擊載荷的方式進行，忽略了實際工況下煤巖與液壓支架的碰撞接觸及接觸時煤巖顆粒的落點與沖擊方式差異，這與實際工況不符。筆者主要針對單顆粒煤巖以不同的下落沖擊方式沖擊尾梁不同位置，從而得出尾梁承受不同沖擊載荷后的動態響應。通過對尾梁受單顆粒煤巖沖擊得到的動態響應分析，為沖擊載荷作用下整個液壓支架的分析提供研究基礎。

1 液壓支架剛柔耦合模型的建立

筆者采用 ZF5600/16.5/26 型液壓支架，為了提高計算機仿真計算效率，對尾梁進行了簡化處理。尾梁與水平面的夾角為 40°，煤巖顆粒用半徑為 40 mm的球體代替，采用 SolidWorks 建立如圖 1 所示的放頂煤液壓支架結構模型。

將液壓支架結構模型中的掩護梁、尾梁以及球體導入 HyperMesh 中劃分網格、定義材料屬性，生成柔性體，如圖 2 所示。其中柔性體尾梁的網格數量為479 977 個，柔性體球體的網格數量為 301 379 個，柔性體掩護梁的網格數量為 729 251 個。

將放頂煤液壓支架機構導入 ADAMS，并且利用HyperMesh 生成的柔性體掩護梁、尾梁和球體替換原來模型中相應的剛性體。尾梁平衡千斤頂主要作用是支撐尾梁，直到穩定后達到平衡狀態，其運動特性與ADAMS 中的彈簧阻尼系統的特性相對應，所以可以用彈簧阻尼系統等效替代尾梁平衡千斤頂。建立的液壓支架剛柔耦合模型如圖 3 所示。

圖1 放頂煤液壓支架結構模型Fig.1 Structure of hydraulic support of caving top coal

圖2 部件網格劃分Fig.2 Mesh division of component

尾梁、掩護梁及煤巖顆粒的材料參數如表 1 所列，其他剛性體部件的材料均為 Q345。

2 等效彈簧阻尼模型

煤巖顆粒沖擊尾梁時，尾梁會對平衡千斤頂施加外力作用，導致千斤頂缸體內的乳化液體積發生變化，在一定意義上，缸體和乳化液相當于固體和液體2 個彈簧，串聯之后組成了千斤頂系統，因此千斤頂的等效彈簧剛度ks可以根據固液彈簧耦合理論[7]給出的計算公式計算，

圖3 液壓支架剛柔耦合模型Fig.3 Rigid-flexible coupling model of hydraulic support

表1 尾梁、掩護梁以及煤巖顆粒的材料參數Tab.1 Material parameters of tail beam,shield beam and coal rock particle

式中：kq為乳化液剛度；kg為千斤頂缸體剛度。

本文中的放頂煤液壓支架均采用單伸縮千斤頂，其等效彈簧剛度

式中：d為缸體內徑；δ為缸體壁厚；Es為缸體彈性模量；L為乳化液液柱高度；kl為乳化液體積壓縮系數。

乳化液體積壓縮系數kl和乳化液體積彈性模量El具有以下關系

結合式 (2) 和 (3)，得

由此可根據千斤頂中乳化液的高度來計算彈簧阻尼模型中的等效彈簧剛度。缸體材料為 Q345，缸體和乳化液的工程參數如表 2 所列。

3 接觸方式的選取及接觸參數的確定

運用 ADAMS 對 2 個物體之間的接觸碰撞進行定義時，有恢復系數法和沖擊函數法[8]2 種定義方式。相比來說，恢復系數法的參數更難準確設置，因此，筆者采用沖擊函數法對煤巖與尾梁之間的接觸進行定義。

表2 缸體和乳化液的工程參數Tab.2 Engineering parameters of cylinder body and emulsion

(1) 接觸剛度k接觸剛度k是 Impact 接觸函數在定義碰撞接觸時最重要的模型參數，其數值大小與2 個接觸物的力學屬性和接觸面形狀有關。當煤巖顆粒沖擊尾梁時，接觸位置的面積與接觸物體相比是完全可以忽略的。煤巖顆粒和尾梁之間的接觸不考慮摩擦，因此在確定接觸剛度k時，可以采用 Hertz 接觸理論來進行計算，計算公式[9]為

式中：R1、R2分別為 2 個碰撞物體接觸處的半徑；E1、E2分別為 2 個接觸物體的彈性模量；μ1、μ2分別為 2 個接觸物體的泊松比。

本文中煤巖球體的半徑為 40 mm，煤巖球體和尾梁的材料參數參考表 1 給出的數據，根據式 (5) 可以得出k=2.045 763 312×104N/mm。

(2) 非線性指數 非線性指數代表了材料的材料剛度項對于法向接觸力的貢獻指數，可查閱 ADAMS幫助文件中的常用材料非線性材料指數表確定，筆者選取的金屬非線性指數為 1.5。

(3) 阻尼系數 阻尼系數與接觸過程中的能量損耗有關，一般為剛度系數的 0.1%～ 1.0%。

(4) 最大侵入深度 最大侵入深度指的是阻尼系數增長到最大值時，2 個接觸物體間的相互切入距離，取默認值 0.1 mm。

4 2 種不同落煤方式對于尾梁動態特性的影響

在綜采放頂煤過程中，煤巖下落的方式有很多種，筆者采取的沖擊尾梁的方式有 2 種：一種是相同初始下落速度，不同下落角度；另一種是相同接觸速度，不同接觸角度。具體過程為：首先選擇尾梁上的中心點，沿尾梁頂板方向在中心點左右 300 mm 各取1 個點，此均勻分布的 3 個點作為此沖擊尾梁的接觸點，如圖 4 所示。

圖4 尾梁沖擊點Fig.4 Impact point of tail beam

第 1 種沖擊尾梁的方式如圖 5 所示，統一設置煤巖球顆粒的初速度為 6 m/s，下落角度α(下落方向與水平方向夾角) 分別為 5°、10°、15°、20°、25°。

圖5 下落角度Fig.5 Falling angle

第 2 種沖擊尾梁的方式如圖 6 所示，統一設置煤巖球顆粒的接觸速度為 8 m/s，接觸角度β(沖擊方向與豎直方向的夾角) 分別為 0°、5°、10°、15°。

4.1 相同下落速度，不同下落角度對尾梁沖擊產生動態特性的影響

在下落速度相同的情況下，隨著下落角度不斷變化，下落速度在x、y軸方向發生變化，進而導致最終的沖擊合速度及分速度不同。初速度設置為 6 m/s，通過勾股定理和自由落體定律分別得出初始分速度與最終合速度，如表 3 所列。

圖6 接觸角度Fig.6 Contact angle

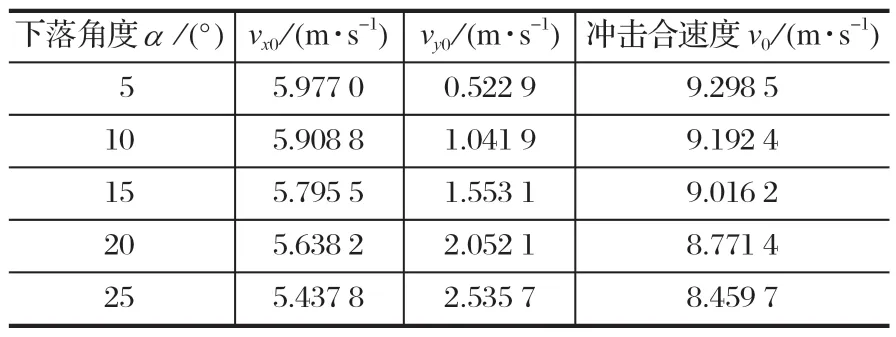
表3 煤巖顆粒下落初速度與沖擊合速度Tab.3 Initial falling velocity and resultant impact velocity of coal rock particles

煤巖顆粒分別沖擊在尾梁的 3 個點處，尾梁產生的接觸力以及動態響應變化情況如下：

尾梁受到沖擊時的最大接觸力變化情況如圖 7 所示，3 條曲線的走勢基本上一樣，最大接觸力隨著下落角度的增加呈現出減小的趨勢。當下落角度較小時，3 個點之間的最大接觸力相差較大；下落角度逐漸變大，3 個點之間的最大接觸力差值趨于平緩，接近 25°時差距越來越不明顯。3 個點之間的接觸力從a點到c點依次減小，而且隨著下落角度的增大，3個點之間的接觸力差距越來越小。

圖7 相同下落速度，不同下落角度時，尾梁最大接觸力Fig.7 Maximum contact force of tail beam at same falling velocity and various falling angle

煤巖顆粒沖擊尾梁的接觸力隨著下落角度的增加而呈現減小趨勢的原因是煤巖顆粒對尾梁的有效沖擊減弱。此沖擊方式中設置的沖擊角度全都是垂直尾梁頂板，但是下落角度的不同使得最終沖擊尾梁的合速度不同。當下落角度增加時，尾梁處煤巖顆粒的水平初速度減小，垂直速度增加，煤巖顆粒在水平方向做勻速運動，在豎直方向做自由落體運動，最終的沖擊合速度減小，也就是說，最終給予尾梁的沖擊減小，產生的沖擊激勵減弱。

尾梁受沖擊處的最大速度變化如圖 8 所示，最大速度隨著煤巖顆粒下落角度的增大而逐漸減小，3 個點位置的速度從a點到c點依次增大。

圖8 相同下落速度，不同下落角度時，尾梁最大速度Fig.8 Maximum velocity of tail beam at same falling velocity and various falling angle

尾梁的最大速度響應和接觸的最終合速度的變化趨勢是一致的，都是隨著下落角度的增大而增大，這是一種速度和能量的轉換現象。從a點到c點的最大速度依次變大，是因為a點離尾梁與掩護梁之間的鉸接點最近，c點離尾梁與掩護梁之間的鉸接點最遠，由此可見，尾梁在c點的自由振動要大于a、b點的自由振動，其所產生的速度更大。

尾梁的最大加速度變化情況如圖 9 所示。3 條曲線的走勢基本一致，最大加速度隨著下落角度的增加呈現出減小的趨勢。隨著下落角度的增加，尾梁 3 個沖擊點位置的最大加速度響應差異越來越小。尾梁b點的加速度均大于a點與c點的加速度。

由圖 9 可知，煤巖顆粒給予尾梁的沖擊激勵隨著下落角度的增加呈現出減小的趨勢，即給予尾梁的沖擊力減小，導致尾梁產生的加速度也呈現減小的趨勢，這符合牛頓第二定律。尾梁的中心點在左側受到掩護梁和尾梁鉸接點的約束，在右側受到彈簧阻尼的約束；a點位置在左側受到掩護梁和尾梁鉸接點的約束，在右側受到彈簧阻尼的約束較??；c點位置在左側受到掩護梁和尾梁鉸接點的約束較小，在右側受到彈簧阻尼的約束；相同沖擊力的情況下，越靠近中間位置，加速度越大，是因為此處加速度的傳遞效果越好。

圖9 相同接觸速度，不同接觸角度時，尾梁最大加速度Fig.9 Maximum acceleration of tail beam at same contact velocity and various contact angle

4.2 相同接觸速度，不同接觸角度對尾梁沖擊產生動態特性的影響

設置煤巖顆粒與尾梁接觸時的速度均為 8 m/s，沖擊角度的變化使得接觸分速度不斷變化。煤巖顆粒沖擊尾梁的角度分別為 0°、5°、10°、15°，豎直方向的下落分速度均為 1.0 m/s，具體參數設置如表 4所列。

表4 煤巖顆粒與尾梁的接觸速度Tab.4 Contact velocity of coal rock particles with tail beam

圖10 相同接觸速度，不同接觸角度時，尾梁最大接觸力Fig.10 Maximum contact force of tail beam at same contact velocity and various contact angle

在相同接觸速度、不同接觸角度時尾梁的最大接觸力變化如圖 10 所示。隨著接觸角度的增加，a、b、c3 個點的最大接觸力依次增加，而且在相同接觸角度的情況下，最大接觸力的變化是由a到c逐漸減小。

在此沖擊的情況下，接觸時的合速度是一致的。隨著接觸角度的不同，使得垂直于尾梁和平行于尾梁的分速度產生變化，那么煤巖顆粒對于尾梁的有效沖擊就會產生變化。當接觸角度增加時，垂直于尾梁頂板的分速度增加，平行的分速度減小，所以產生的接觸力逐漸增大。

尾梁接觸處的最大速度如圖 11 所示，最大速度隨接觸角度的增加而增加，且從a點到c點的最大速度呈上升趨勢，其中b點與c點的最大速度值相近。從接觸速度到尾梁速度的變化，是一種速度傳遞現象。當煤巖顆粒與尾梁接觸角度增加時，煤巖顆粒給予尾梁的力沿垂直于尾梁頂板的方向增大，帶來的能量增大，通過動能守恒原理，尾梁獲得的相對動能在增加，導致尾梁的速度也呈上升的趨勢。b點與c點都在遠離掩護梁與尾梁的鉸接點位置，此 2 處的自由振動相近且大于a點，因此b點與c點的最大速度相近且遠大于a點的最大速度。

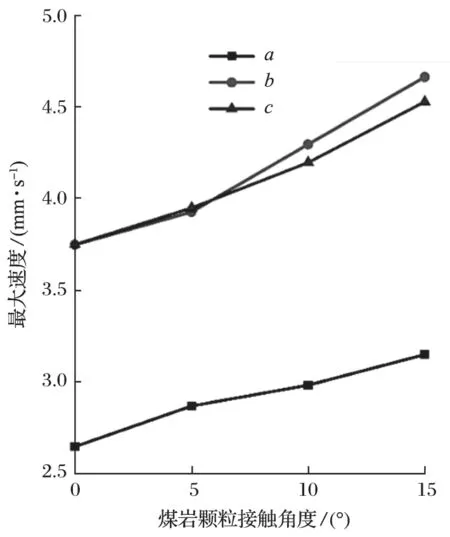
圖11 最大速度Fig.11 Maximum velocity

尾梁接觸處的加速度如圖 12 所示，煤巖顆粒給予尾梁的沖擊激勵隨著接觸角度的增加呈現增強的趨勢，即給予尾梁的沖擊力增大，導致尾梁產生的加速度也呈現出增加的趨勢。

4.3 尾梁與掩護梁鉸接點處力的變化

在煤巖顆粒以相同接觸速度、不同接觸角度對尾梁沖擊的前提下，對尾梁與掩護梁鉸接點處的力變化進行研究分析。尾梁與掩護梁鉸接點處受力情況如圖13 所示。

圖12 最大加速度Fig.12 Maximum acceleration

圖13 鉸接點受力情況Fig.13 Force state at hinge point

由圖 13(a) 可知，尾梁與掩護梁鉸接點處的力從煤巖顆粒下落到煤巖顆粒沖擊到尾梁上是一個動態變化過程，在產生沖擊接觸之前，尾梁在重力與彈簧阻尼系統的作用下先作自由振動運動后達到平衡穩定，鉸接點力的變化趨勢與其相同；當煤巖顆粒沖擊尾梁的瞬間，鉸接點位置的力瞬間增大，隨后又在彈簧阻尼系統的作用下達到穩定。

由圖 13(b) 可知，鉸接點處的力隨著接觸角度的變化而變化。當沖擊帶來的能量能夠最大程度轉化為尾梁接受的能量時，鉸接點處的力會變大，反之亦然。在圖 13(b) 中，鉸接點處的力隨著接觸角度的增加而增加，這是因為隨著接觸角度的增加，煤巖顆粒與尾梁之間的能量轉換的效率在增大。

5 結論

以不同角度落煤沖擊液壓支架尾梁，模擬了放頂煤過程中實際采煤工況下的落煤方式；煤巖顆粒以不同角度接觸沖擊液壓支架尾梁，反映了放頂煤過程中煤巖垮落時液壓支架尾梁產生的各種動態響應，更貼近實際情況。

(1) 以不同下落角度和不同接觸角度的方式落煤，尾梁的動態響應隨角度的變化而變化。這是一種能量的轉化方式，即相同速度、不同角度的情況下，哪個給予尾梁的有效沖擊能量最大，那么它給尾梁帶來的沖擊就最大，產生的沖擊力也最大；鉸接點處受力情況與尾梁基本一致。

(2) 以相同的方式沖擊尾梁的不同位置，產生的接觸響應不同，這與尾梁受到的約束以及等效阻尼系統帶來的自由振動有關。相同情況下，越接近尾梁的末端產生的速度響應越大，因為此位置的自由振動較大，運動趨勢更加明顯。

(3) 所研究的 2 種不同的落煤方式沖擊尾梁，克服了煤巖直沖尾梁的不足，在一定程度上還原了放頂煤開采實際工況，充實了有關放頂煤過程中沖擊尾梁的仿真試驗研究，為沖擊載荷作用下整個液壓支架的分析提供了研究基礎。