基于滑模觀測器的煤礦帶式輸送機用永磁同步電動機控制系統研究
晉城煤炭規劃設計院 山西晉城 048000
在 煤礦運輸系統中帶式輸送機是重要設備之一。近年來,國外單機帶式輸送機運距已超過 30 km,已在澳大利亞礦山投入使用;在德國煤礦使用的大型帶式輸送機,其輸送量己達 37 500 t/h,運行速度達 7.4 m/s。目前國產帶式輸送機的理論研究越來越受到重視,在大運量輸送機控制技術和遠程控制領域取得了長足的進步,逐漸淘汰了傳統的驅動方式。隨著永磁同步電動機 (Permanent Magnetic Synchronons Motor,PMSM) 及其控制系統的發展,煤礦帶式輸送機的驅動方式也更加智能,設計一種高效、智能的帶式輸送機控制系統,對建設現代化、智能化礦井具有十分重要的意義。
筆者設計了一種以滑模觀測器 (Sliding Mode Observer,SMO) 算法為基礎的 PMSM 驅動的帶式輸送機控制系統,通過分析 PMSM 兩相靜止坐標系下的數學模型,提出了基于鎖相環轉子位置估計的SMO 算法,進而搭建了基于 SMO 算法的 PMSM 無位置傳感器控制系統仿真模型,并通過仿真結果分析驗證了該控制系統的有效性和合理性。
1 帶式輸送機驅動系統分析
1.1 異步電動機驅動系統
傳統的帶式輸送機驅動系統主要由異步電動機、減速器和聯軸器組成,如圖 1 所示。異步電動機驅動系統具有便于操作、啟動轉矩小及控制系統簡單等優點;其缺點是啟動電流較大、控制精度差、傳動效率低、能耗高,聯軸器和減速器故障率高,后期維護費用較高。
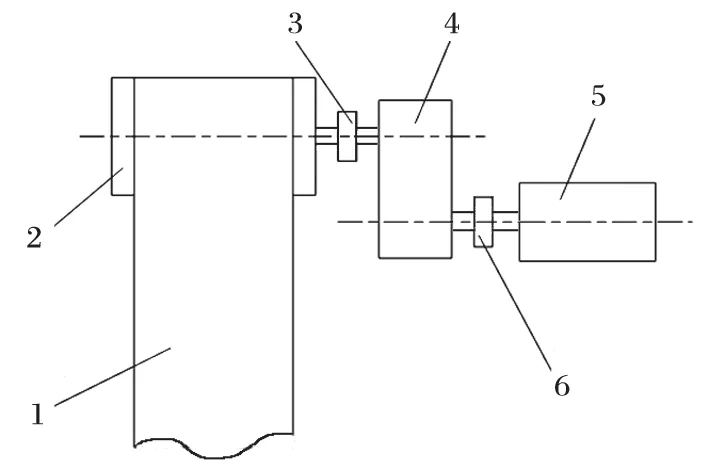
圖1 異步電動機驅動示意Fig.1 Sketch of asynchronous motor drive
1.2 PMSM 驅動系統
新型的帶式輸送機驅動系統主要由 PMSM 和變頻器組成,如圖 2 所示。與異步電動機驅動系統相比,PMSM 驅動系統傳動效率高,能耗較低,節約電能;電動機啟動轉矩大,具有較強的過載性能和軟啟動性能;系統結構簡單、便于維護;變頻調速性能高,多電動機驅動時功率平衡性好[1]。因此,選用由PMSM 和變頻器組成的新型帶式輸送機驅動系統具有十分明顯的優勢。
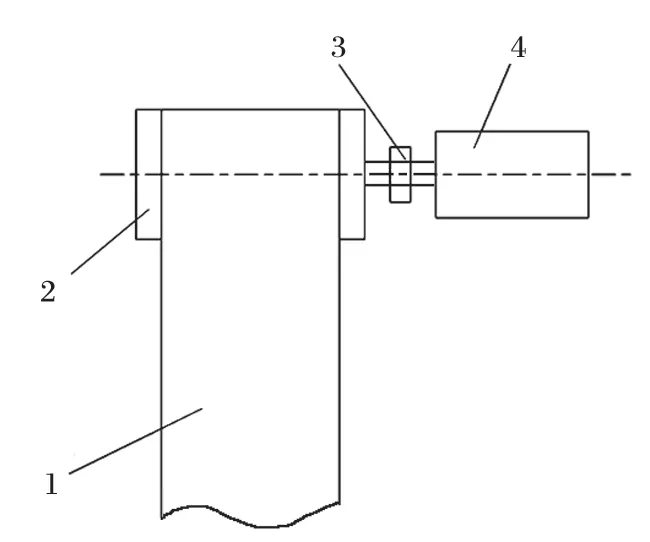
圖2 PMSM 驅動示意Fig.2 Sketch of PMSM drive
2 帶式輸送機控制系統數學模型
2.1 PMSM 數學模型
在 PMSM 的控制方式中,滑模控制是一種特殊的變結構控制,它將電動機作為一種離散型的系統進行控制,表現為控制的不連續性和非線性。該控制系統的轉速響應在相平面里跟蹤轉速的估計值,具有較強的魯棒性,不受 PMSM 參數和負載變化的影響。SMO 控制結構簡單,將控制系統的狀態變量控制在滑模面上進行高頻率、小幅度的滑模運動[2]。筆者設計的 SMO 算法是基于靜止坐標系α-β下的數學模型,PMSM 電壓方程為[3]
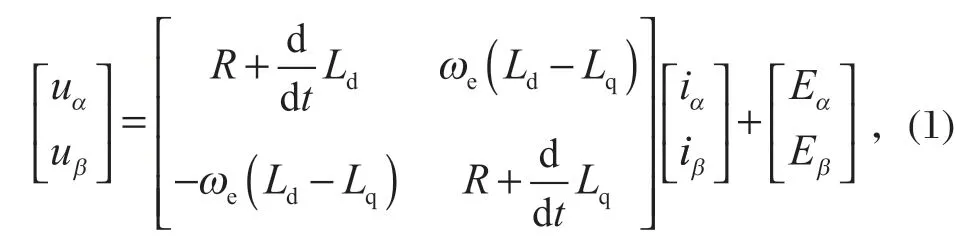
式中:[uαuβ]T為定子電壓;R為定子電阻;Ld、Lq為定子電感;ωe為電角速度;[iαiβ]T為定子電流;[EαEβ]T為擴展反電動勢[4],且滿足
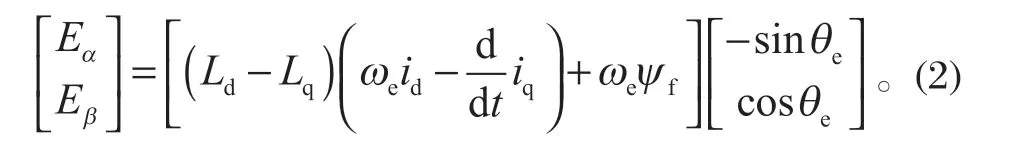
式中:ψf為永磁體磁鏈;θe為轉子位置角。
由式 (2) 可知,PMSM 的擴展反電動勢包含電動機轉子位置和轉速的全部參數,只有準確獲取擴展反電動勢,才可以計算出電動機的轉速和轉子位置信息。為便于用 SMO 來觀測擴展反電動勢,將式 (1) 改寫為電流狀態方程,
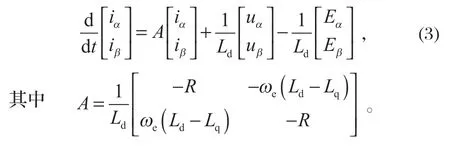
2.2 SMO 數學模型
2.2.1 SMO 的設計
定子電流觀測值方程為

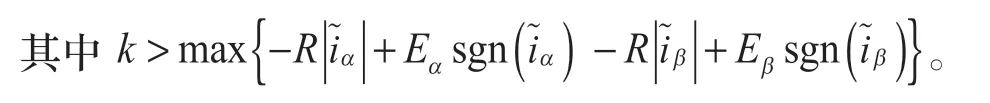
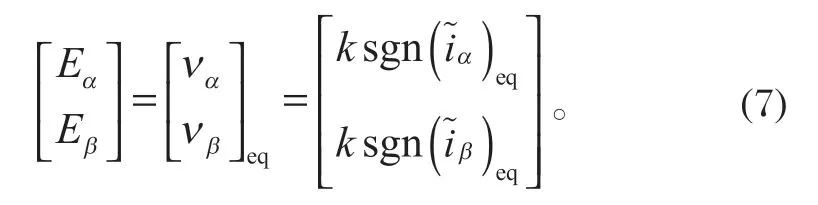
2.2.2 基于鎖相環的轉子位置估計
根據式 (2),SMO 算法需要進行反電動勢信號的提取,而傳統 SMO 的 PMSM 無位置傳感器控制系統采用的是低通濾波器。低通濾波器會造成轉子位置估算的相位延時,使控制系統產生較大的抖振,轉子位置的估計值存在一定的高頻波動[5]。采用基于鎖相環的轉子位置估計算法能夠有效減小系統抖振和相位延時。因此,筆者采用鎖相環系統估算轉子位置信息,其原理框圖如圖 3 所示[6]。
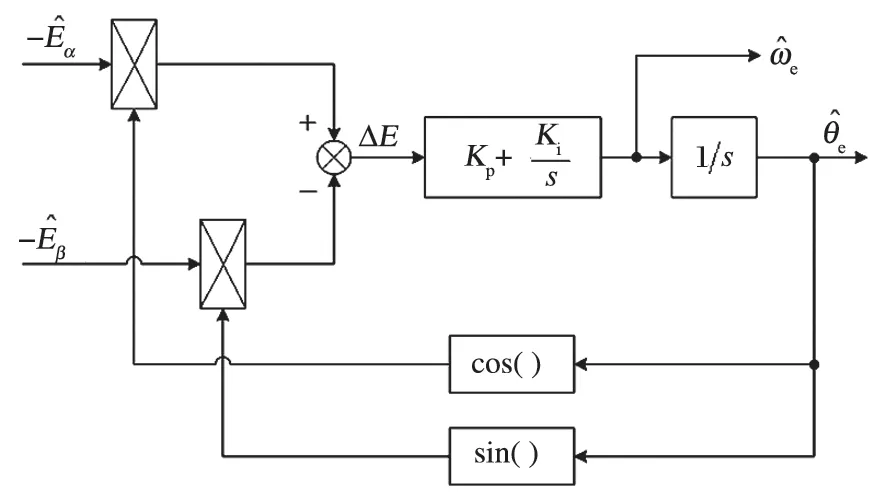
圖3 鎖相環原理框圖Fig.3 Principle block diagram of phase locked loop (PLL)
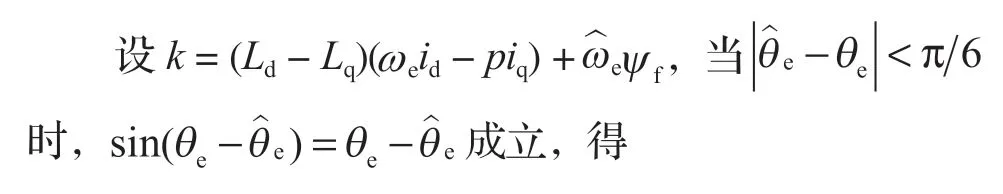
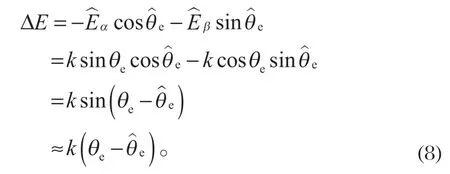
由式 (8) 可知,鎖相環原理可以等效為圖 4 的框圖。
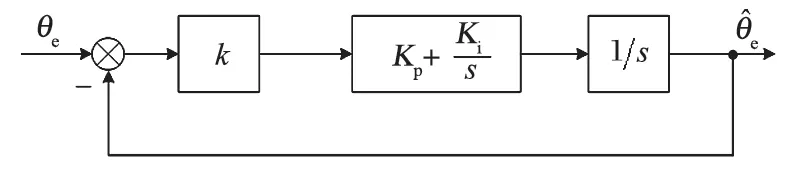
圖4 鎖相環等效框圖Fig.4 Equivalent block diagram of PLL

式中:ξ為 PI 調節系數;ωn為電動機轉速變化值。
2.3 基于 SMO 的 PMSM 無位置傳感器控制原理
基于 SMO 的 PMSM 無位置傳感器控制方法,采用id=0 的控制策略,在傳統的矢量控制原理的基礎上,增加無位置傳感器的控制策略。其中轉速給定值和轉子位置值均使用 SMO 算法計算出的估計值,從而避免了機械傳感器的使用[7]。基于 SMO 的 PMSM無位置傳感器控制原理框圖如圖 5 所示。
3 基于 SMO 的 PMSM 控制系統仿真建模
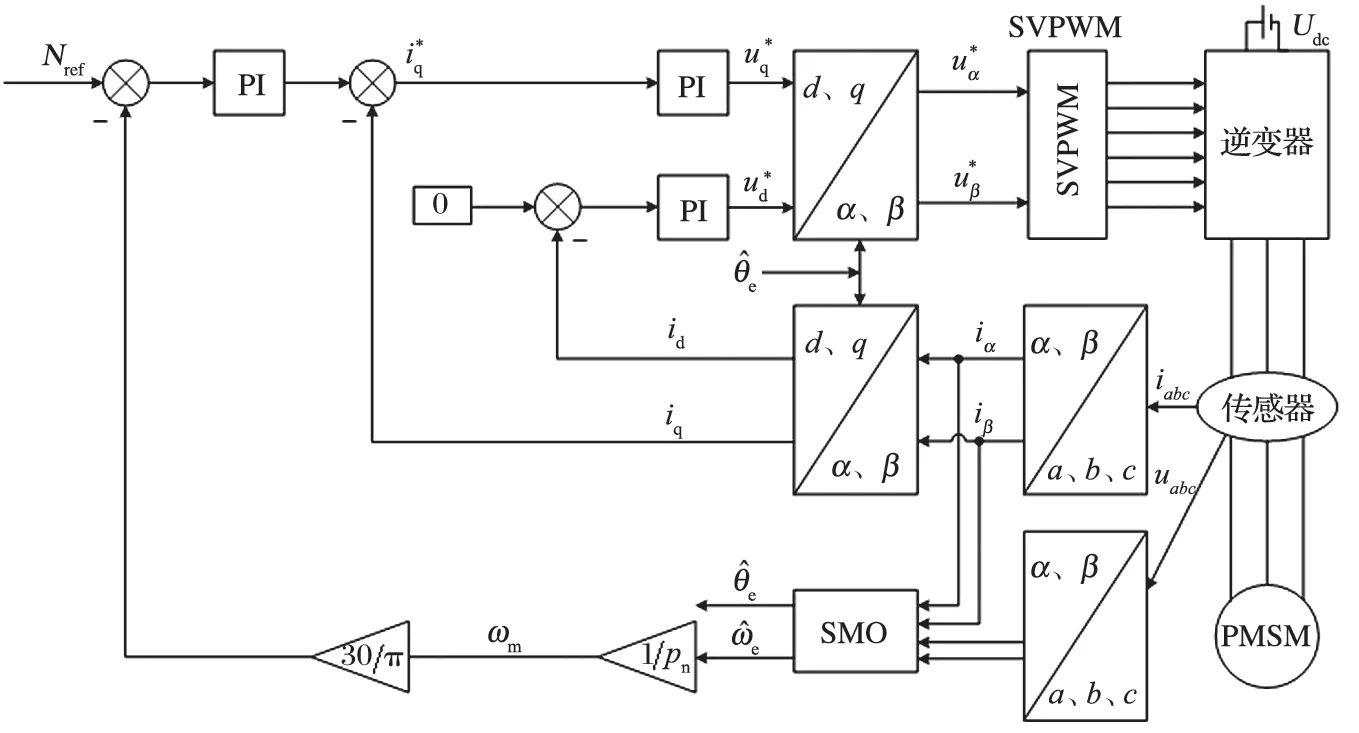
圖5 基于 SMO 的 PMSM 無位置傳感器控制原理框圖Fig.5 Block diagram of PMSM non-position sensor control based on SMO
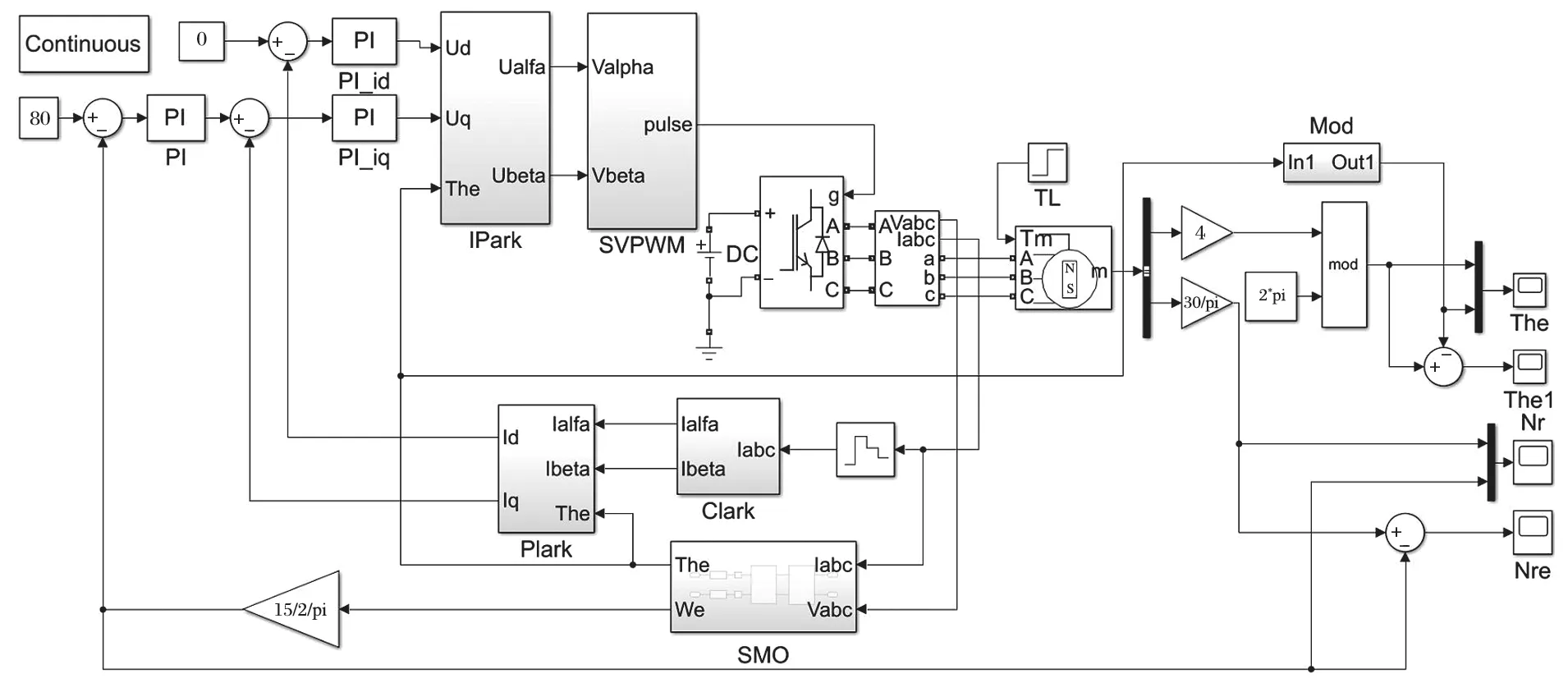
圖6 基于 SMO 的 PMSM 無位置傳感器控制系統仿真模型Fig.6 Simulation mode of PMSM non-position sensor control system based on SMO
根據圖 5 搭建了控制系統的仿真模型,如圖 6所示。仿真模型由 PMSM 模塊、SMO 仿真模型、SVPWM 控制模塊、Plark 變換模塊和 Clark 變換模塊組成[8]。仿真模型中 PMSM 仿真參數設置如表 1 所列。
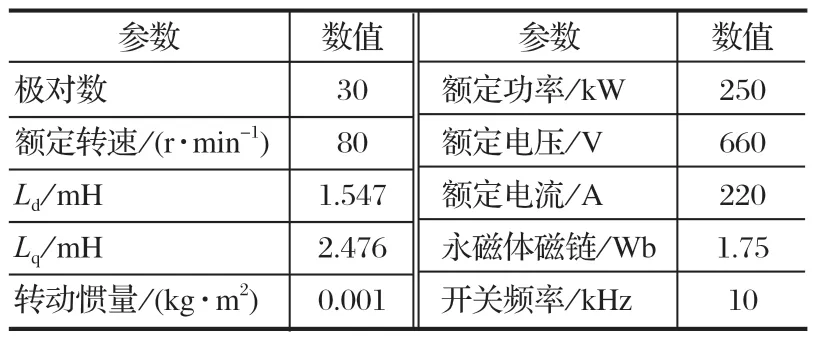
表1 PMSM 仿真參數Tab.1 Simulation parameters of PMSM
SVPWM 控制模塊仿真模型如圖 7 所示,基于鎖相環算法的 SMO 仿真模型如圖 8 所示,鎖相環算法的仿真模型如圖 9 所示,滑模觀測器的仿真模型如圖10 所示。
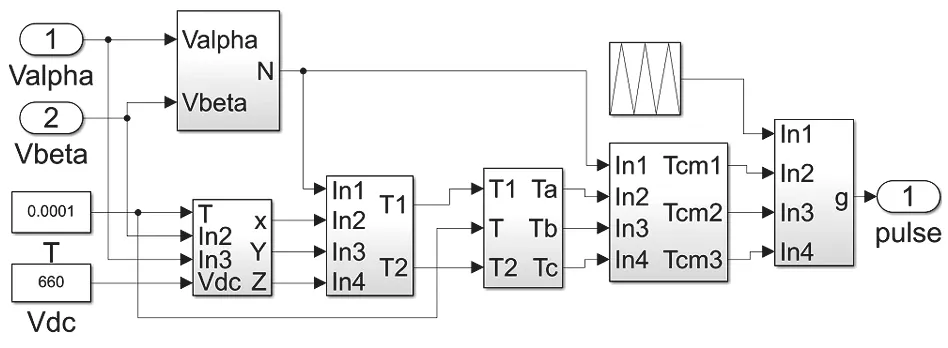
圖7 SVPWM 控制模塊仿真模型Fig.7 Simulation model of SVPWM control module
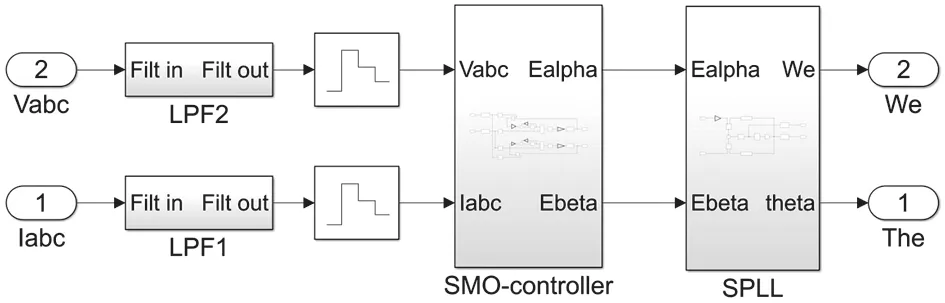
圖8 基于鎖相環算法的 SMO 仿真模型Fig.8 SMO simulation model based on PLL algorithm
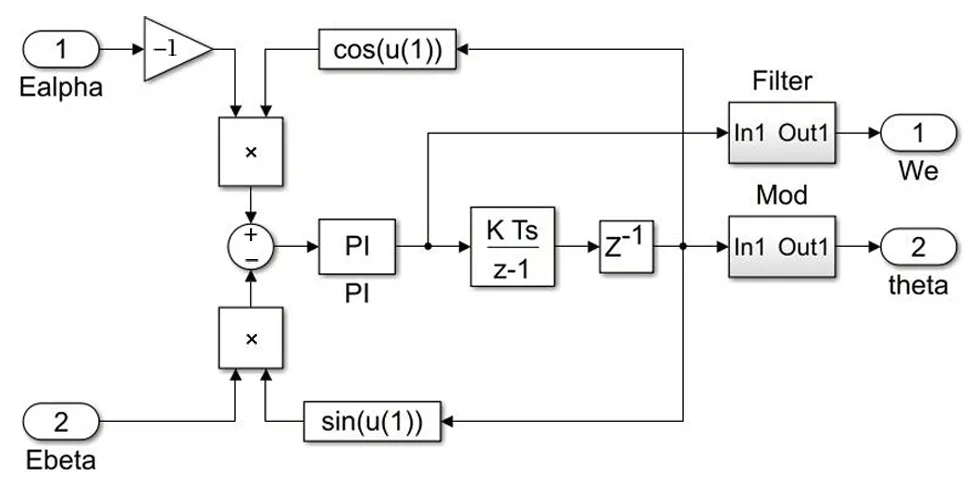
圖9 鎖相環算法的仿真模型Fig.9 Simulation model of PLL algorithm
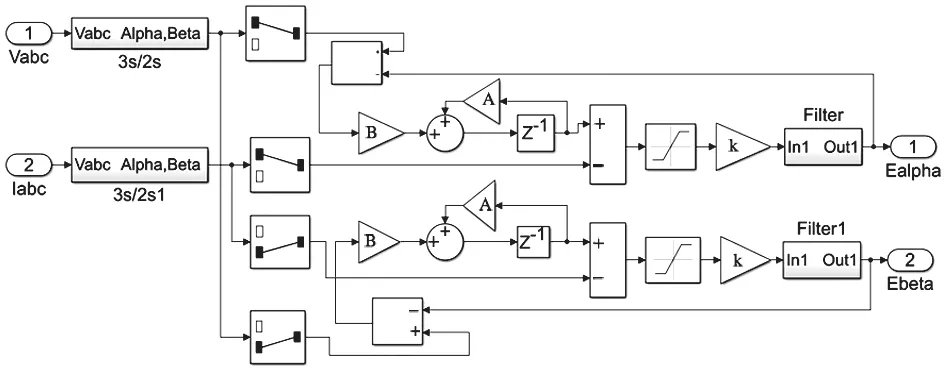
圖10 滑模觀測器的仿真模型Fig.10 Simulation model of SMO
4 仿真結果及分析
PMSM 給定轉速設定為 80 r/min,仿真時間設定為 0.5 s。PMSM 在 0.5 s 內的轉速估計值和實際值波形對比如圖 11 所示。由圖 11 可以看出,PMSM 的實際轉速很快能達到給定值,轉速估計值和實際值波形基本重合,電動機在達到穩定轉速后有 3 r/min 的波動,偏差小于 4%。
PMSM 轉子位置估計值和實際值的波形對比如圖 12 所示,電動機轉子位置估計的電角度和實際的電角度波形基本重合,轉子位置估計值誤差較小。PMSM 轉子位置估計誤差變化波形如圖 13 所示。在電動機啟動時轉子位置估計誤差較大,最大為 0.43 rad;在 0.25 s 附近時轉速趨于穩定,能夠十分精確地跟蹤轉子位置。
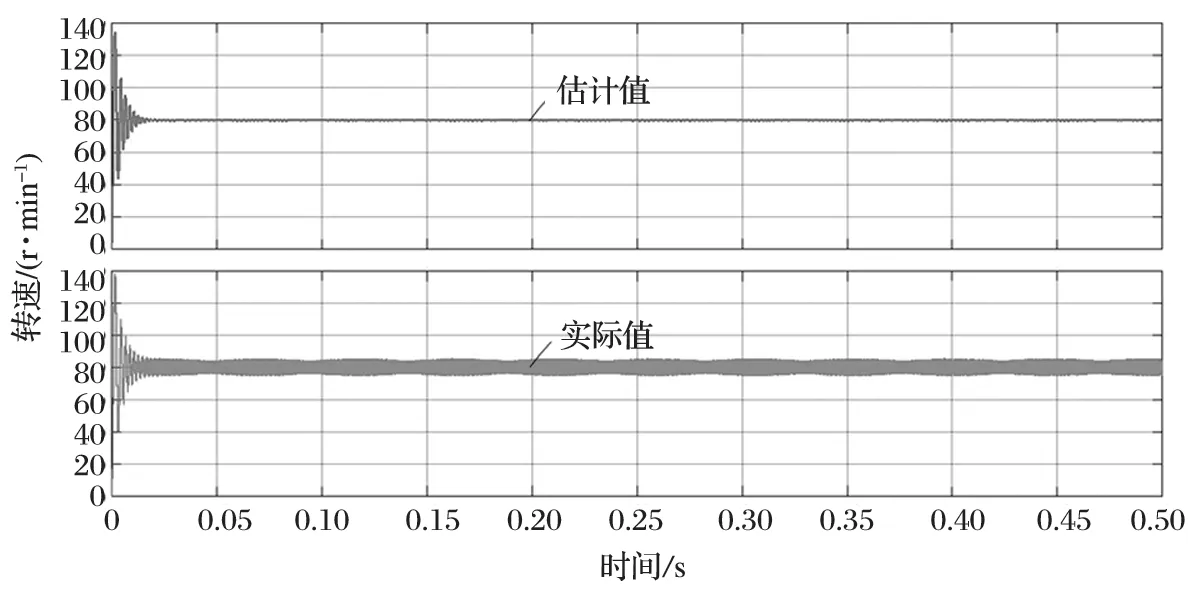
圖11 轉速估計值和實際值波形對比Fig.11 Comparison between waveform of estimated speed value and actual one

圖12 轉子位置估計值和實際值波形對比Fig.12 Comparison between waveform of estimated rotor position value and actual one
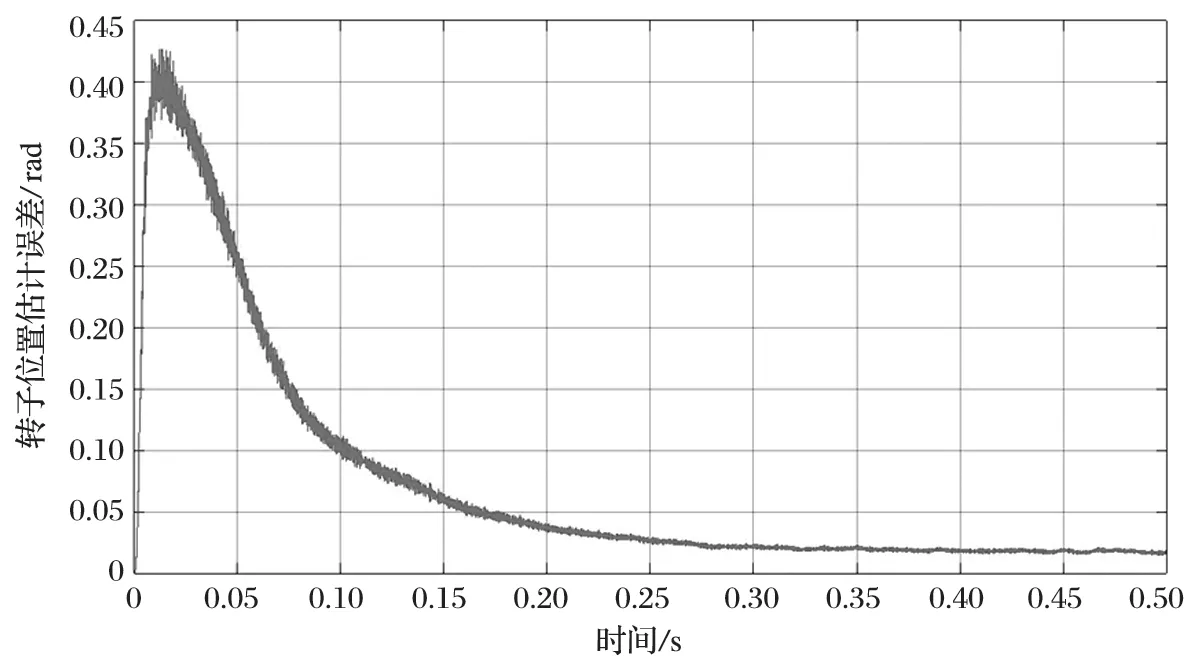
圖13 轉子位置估計誤差波形Fig.13 Waveform of estimation error of rotor position
5 結論
在分析了由 PMSM 和變頻器組成的新型帶式輸送機驅動系統的基礎上,建立了α-β坐標系下的PMSM 的數學模型和 SMO 的數學模型,在 MATLAB/Simulink 仿真軟件中搭建了基于 SMO 算法的 PMSM無位置傳感器控制系統仿真模型,并對仿真結果進行了分析,為新型帶式輸送機驅動控制系統的設計提供了依據。仿真結果證明了基于 SMO 的帶式輸送機用 PMSM 控制系統具有調速性能好、轉速波動小等優點,能夠準確跟蹤轉子位置,轉速估計值精度高,控制系統設計合理,在煤礦帶式輸送機中具有廣闊的應用前景。

