DV-Hop定位算法的研究與改進

劉 超 李海鵬

(西安電子工程研究所 西安 710100)

0 引言

無線傳感器網絡[1-2](Wireless Sensor Networks, WSN)通信系統由大量傳感器組成，用于對監測區域的目標進行檢測、定位和跟蹤等，目標定位算法尤為重要。DV-Hop算法不需要進行角度測量或信號強度測量的設備，具有低成本[3]的優勢，因而獲得了較多研究。DV-Hop算法僅著眼于欲求坐標節點和已知錨節點的平均跳數距離，這種計算方式令節點間距與實際距離存在出入。為了減小誤差值，人們對DV-Hop 算法做出了許多的改進嘗試，如文獻[4]引入的優化均跳距優化和優化位置的改善思路，文獻[5]引入了灰狼算法和極大似然估計的改善思路。就DV-Hop算法中的不足，分析研究后，本文引入了細化半徑的通信方式的方法，以期改善定位精度。

1 DV-Hop定位算法

1.1 無線傳感器網絡技術

如今，不可計數的產品、技術伴隨著無線傳感器網絡的進步走進了人們的視野。其中，在定位技術方面，研究人員把在節點定位階段是否需要進行距離的測量作為評判依據，歸為距離式和無距離式兩種節點定位思路[6-7]。其中，距離式定位技術是通過測量節點間的角度信息或者信號強度信息進行未知節點的坐標估算的,主要包括有AOA算法(Angle of Arrival)、TOA[8]算法(Time of Arrival)、TDOA算法(Time Difference on Arrival)和RSSI算法(Received Signal Strength Indicator)等，上述前三種方法對硬件設備要求較高,這無疑增加了成本;而RSSI算法在信號傳播過程中,信號強度會被障礙物影響而減弱,抗干擾性能較差。典型的無需測距的定位算法主要有DV-Hop算法(Distance Vector-Hop)、質心算法(CentroidAlgorithm)、APIT(Approximate PIT Test)算法等。此類算法不需要測量角度或者測量信號強度的設備，大大降低了成本，因而受到研究人員的歡迎。

1.2 傳統DV-Hop定位算法組成

DV-Hop算法源于美國學者Dragos Niculescu等。其主旨是：首先,獲取未知節點與錨節點的最小跳數、所有錨節點間的平均跳距；其次,未知節點選取周圍任意錨節點的平均跳距作為自身平均跳距值，與自身最小跳數相乘而得錨節點和未知節點間的距離；最后,將距離代入最小二乘法求解欲求節點坐標值。

組成DV-Hop算法的部分有如下文三個階段[9]。

圖1 DV-Hop算法流程圖

1)最小跳數獲取

DV-Hop算法采用距離矢量路由協議的方法，把網絡中每個錨節點的位置坐標信息向周邊的節點進行廣播，每個節點用{xi,yi,hi}表示,其中(xi,yi)就是錨節點i的位置坐標信息；hi表示這個節點到錨節點i的跳數值，初始值均設置成0。

首先，每個錨節點將自身坐標值和跳數值向鄰近節點廣而告之。鄰近節點處于接收到發出消息的狀態后，數據中的跳躍值就會增加1跳，緊接著將更新后的數據轉發給別的鄰居節點，將信息使用泛洪方式傳播。

其次，進行跳數選擇操作：各接收節點將來自同一錨節點跳數值中的最小值保留，其他數值全部舍去。保持網絡的暢通，就能讓全部節點處于獲取每個錨節點最小跳數的狀態。

2)平均跳距的計算

全部節點獲取每個錨節點最小跳數后，可從式(1)獲悉全部錨節點的平均跳距。

(1)

式(1)中，i、j代表錨節點；(xi,yi)、(xj,yj)表示錨節點的坐標；hj表示在i與j不等時錨節點i、j之間的最小跳數；HopSizei表示錨節點i的平均每跳距離。

在網絡中，將獲得的每個錨節點平均跳距進行廣播，當未知節點處于獲悉信息狀態時，選擇一個錨節點平均跳距作為自身的平均每跳距離。此時，全部未知節點u使用式(2)計算距錨節點i的近似距離dui。式(2)中，hui是錨節點i和未知節點u之間的最小跳數。

dui=hui×HopSizeij(i≠j)

(2)

3)未知節點坐標的解算

當獲得的錨節點與未知節點的間距在3個或3個以上時,就能按照最小二乘法進行推理解算獲取所求未知節點的估計坐標值[10]。

利用錨節點i和未知節點u的坐標(xu,yu) 和(xi,yi)可以得到方程(3)為

(3)

未知節點的坐標用公式(4)求得。

(4)

方程(4)可改寫成Ax=B的形式，可得

(5)

(6)

由此可得未知節點u的坐標為

Xu=(ATA)-1ATB

(7)

1.3 傳統DV-Hop定位算法舉例

圖2展示了4個節點的位置關系：A、B、C三個節點是坐標已知的錨節點，N節點作為未知坐標節點。

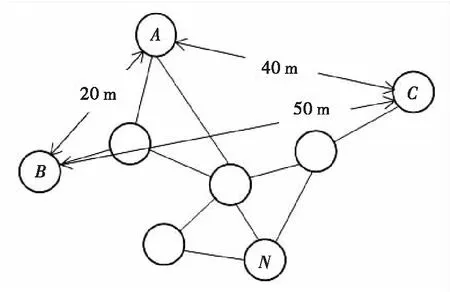
圖2 網絡拓撲結構

由勾股定理得節點A、B的直線距離為20 m，節點A、C的直線距離為40 m，節點B、C的直線距離為50 m。

從圖中跳步路徑可得，2為節點A、B間的最小跳數值，3為節點A、C間的最小跳數值，4為節點B、C間的最小跳數值。

式(8)表示A、B、C三個節點的平均跳距值，對應為

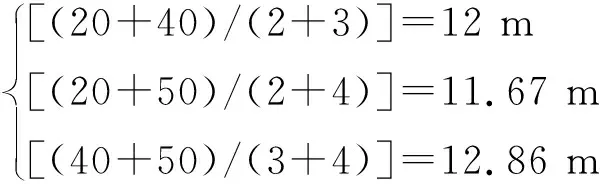
(8)

N取A的平均跳距值，式(9)獲得N節點的估計距離為

(9)

最后，將上述數值代入最小二乘法中推導解算就可以取得未知節點N的預計坐標信息。

2 校正算法

2.1 DV-Hop算法存在的不足

1)跳數信息

通信半徑R內的全部跳數值統一用1表示，與實際情況會產生偏差。比如，把0.3跳的實際跳數籠統的記為1，那么估計距離就會大于實際距離，生出誤差。

2)平均跳距

未知節點的平均跳距值是隨錨節點選取而發生著變化的，不是固定值。這種情況下，生出誤差是在所難免的。

3)計算未知節點坐標的方法

在最小二乘法的推導計算過程中，不能排除得不到(ATA)-1的情況，一旦發生這種情況，就無法成對欲求坐標值的解算，更無定位精度可言。

2.2 改進算法的主旨思想

在DV-Hop 算法跳數獲取環節，只要鄰近節點出現在錨節點半徑為R的通信范圍之內(或等于R)，就統一認為它們間的跳數為1跳。

當圖3所示的情況出現時：已知坐標的3個錨節點，按DV-Hop算法跳數判定方法，統一認為節點O、A與節點O、B的最小跳數值是1跳。實際情況與之不符，最小跳數值統一記為1跳，定會產生有誤差的結果。

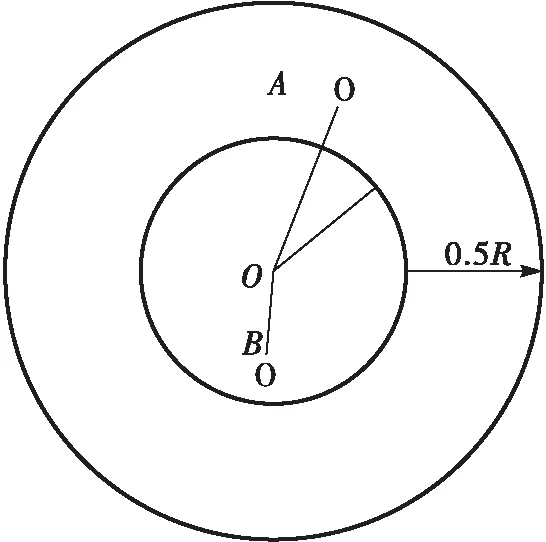
圖3 錨節點分布示意圖

因此，將節點間的跳數細化非常必要，本文利用細化通信半徑的方式達到跳數細化的目的。改進算法將通信半徑細分為0.1R、0.2R、0.3R、0.4R、0.5R、0.6R、0.7R、0.8R、0.9R和R共十種，也就是把通信面積分為了十種，R代表通信半徑。

2.3 改進算法的具體步驟

第一步：最小跳數獲取。

1)初始化網絡，網絡中所有錨節點首次廣播的通信半徑是0.1R，在0到0.1R的圓形區域內通過廣播向范圍內的節點發送自身信息。

當信息傳播范圍內的節點處于接收到信息的狀態后，接收節點獲悉與錨節點的最小跳數值是0.1跳。

2)所有錨節點以0.2R作為廣播的通信半徑，在0到0.2R的圓形區域內通過廣播向影響范圍內的節點發送自身信息。

如果是首次獲得錨節點信息的節點，該節點獲悉與錨節點的最小跳數值是0.2跳。若該節點之前就獲取過信息，仍保留0.1跳的數值。

3)以此類推，在之前通信半徑的基礎上每次增加0.1R進行錨節點的第三、四、五、六、七、八、九和十次廣播，得到最小跳數值。在通信半徑變化的情況下，通過改變傳感器的發射功率來實現傳感器廣播范圍的變化。

第二步：平均跳距的計算。

使用勾股定理求取錨節點間的直線距離，再使用式(1)獲取全部錨節點的平均每跳距離值。

第三步：解算未知節點坐標。

任意選取一個錨節點的平均每跳距離作為未知節點平均跳距進行節點間距離計算。

最后，按照最小二乘法解算獲取未知節點的坐標值。

3 仿真實驗的結果與分析

3.1 仿真環境

使用計算機中Matlab R2016a軟件形成邊長100 m的正方形，并在其中任意分布100個節點。在錨節點數目一致的情況下，設計進行多組實驗,利用蒙特卡洛方法得到定位誤差平均值。本文選取相對定位誤差作為評價標準，如式(5)為

(5)

其中，N為節點總數；u為錨節點數目；R為節點的通信半徑；(xi,yi)，(Xi,Yi)分別表示未知節點i的估算坐標與實際坐標。

仿真參數如表1所示。

表1 實驗仿真參數

節點隨機分布圖如圖4所示。

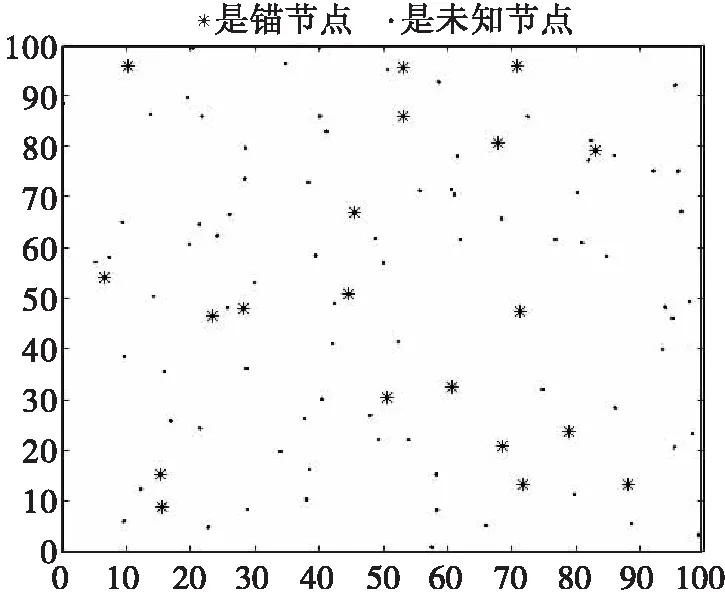
圖4 節點隨機分布圖

3.2 仿真結果分析

仿真結果如圖5所示。

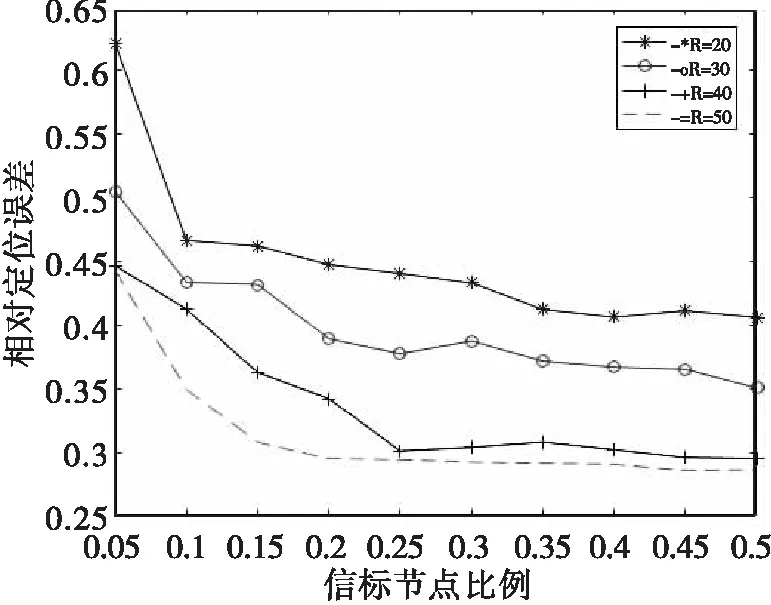
圖5 4種半徑對應的原算法相對定位誤差與錨節點百分比的關聯示意圖

由圖4與圖5分析可得：

1)通信半徑統一的前提下，隨錨節點百分比的變大，原算法的相對定位誤差呈減小的趨勢。

2)錨節點百分比統一的基礎上，當通信半徑逐步變大時，原算法的定位誤差也呈下降態勢，但是降幅在逐步趨小。

3)實際的工程應用時，通信半徑不是越大就越好的，因為隨著通信半徑變大，就需要更大的能量，會增加相應的成本。

4)仔細觀察可得個別點的相對定位誤差會略高于前邊的點，這是網絡拓撲造成隨機產生的緣故。

圖6至圖9說明：在以上4種半徑下進行節點定位，改進算法的相對定位誤差值有大幅的減少。這說明節點間的跳數細化對降低相對定位誤差的效果是積極的。

圖6 R=20m

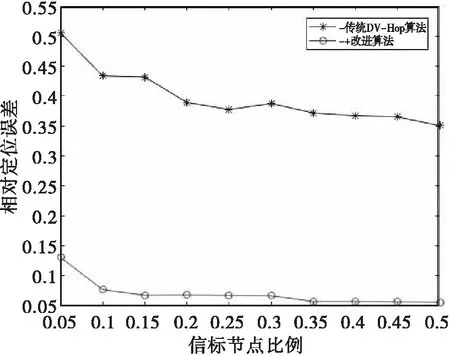
圖7 R=30m

圖8 R=40m

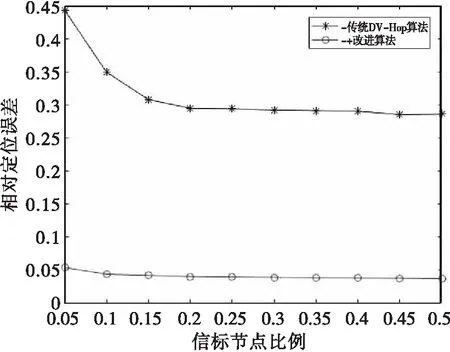
圖9 R=50m

誤差降低值如表2所示，改進算法相較于原算法削減了16%～39%的相對定位誤差。

表2 改進算法在差別半徑下的誤差降低值

4 結束語

本文首先研究了經典DV-Hop算法，經分析發現了存在的缺陷，以跳數信息的不足為切入點，引入通信半徑細化的改善算法，獲得了細化的跳數和較為準確的節點間距值。

經由Matlab仿真實驗，結果說明：在平等仿真前提下，改進算法在沒有大幅度增加算法復雜度的背景下有效降低了定位誤差，實現了提高定位精度的目的。

然而本文提出的改進算法的優勢只是對定位精度的改善，對多次通信半徑的廣播和泛洪中能耗所產生的花銷沒有考慮在內。未來應著重研究在不影響定位精度的前提下，降低改進算法的成本。