粒子群優化算法在電力工程三維數據聚類分析中的應用

伍家耀，周鯤，徐志強，劉立洪

（湖南經研電力設計有限公司，湖南長沙 410000）

電力工程設計中變電站的選址、輸電線路的規 劃等各有不同特點，因此需要對多個專業的大量實際勘測數據進行處理。準確分析及提取各專業數據的有效特征是電力工程設計的關鍵性依靠，有效特征能夠提供全方位的設計依據，最終實現電網安全、穩定經濟運行，從而真正提高投資效益[1-2]。

高效統計、分析電力工程大數據有利于電力部門掌控電力工程設計的實地數據處理信息，實現精細化管理，提供更加合理、優質的電力工程設計方案，對工程后續的全面開展提供可靠的實施方案。現有的電力工程設計資料不再單獨地以二維平剖面圖件為主，而是與其他多源、多專業、多專題成果進行協同實現三維設計。三維數據信息以二圖專題件與三維模型的形式在統一平臺中直觀展示，給設計人員提供全專業、多專題的信息。電力工程中的三維設計亟需可靠地處理數據，并高效篩選出有效數據[3-5]。傳統的數據處理方法中數據分析繁重、偽數據多的現象較為普遍。隨著數據分析方法的不斷成熟與進步，不同類型處理方法受限于實際的數據應用條件，難以直接有效地處理三維數據，更不能準確擬合數據并提取數據特征，數據受干擾程度較高，難以實現有效的數據擬合?；诖?，尋找一個合適的最優化目標函數是分析最優電力工程三維數據的關鍵。

為此，該文結合電力工程三維數據信息構建了最優化目標函數，粒子群能對大量的三維數據建立智能模型，從而更加有效地擬合三維數據，并利用粒子群算法的適應度函數進行最優搜索，最終提供可靠的電力工程設計方案。

1 粒子群優化算法

1995 年提出的粒子群優化算法是基于社會體系中各個角色的相互制約關系，而最終提出的全局優化算法。通過各個角色之間的聯動及制約關系修正各角色之間的行動策略，最終求取最佳的優化解[6]。

假設存在m個粒子在D維的目標搜尋空間，,i=1,2,…,m表示第i個粒子 在維度空間的位置，即每個粒子所在的D維空間位置是一個可能解[7-8]。然后，尋找適合的目標函數并將位置代入其中。根據計算值判定適應值的 優 勢與劣勢，進而優化并獲得解。粒子存在一個速度值特征，其存在的特性用,i=1,2,…,m進行表示。通過前期的適應性搜索，找尋到最優位置，即最優解,i=1,2,…,m。通 過下列公式能夠得到粒子群的最優化算法：

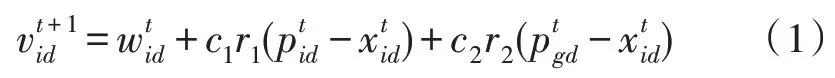
其中，i=1，2，…m；d=1，2，…，D；ω指粒子的慣性特性，使粒子保持運動慣性，這樣可以保證粒子具有較強的空間搜索能力，從而使粒子探尋新區域，最終獲得最佳解。c1和c2稱作學習因子，均是非負常數，其特性表征將每個慣性粒子推向個體最優位置pbest和群體最優位置gbest的統計加速項的權重。其值較低的粒子，在被糾正之前是允許在目標區域外徘徊的，而其值較高的粒子則會沖出目標區域；r1和r2是介于[0，1]間的隨機數。vid介于最大值vmax與最小vmin之間，是一個常規常數，由用戶的學習習慣決定，其能決定區域分辨度，從而確定當前位置與最優位置間區域的精度。若存在vmax過高，粒子可能會偏離最優解方向，從而錯過最優解。若vmax過小，則可能會尋找到最優解，但也很可能存在局部最優解情況，從而無法得到全局最優解[9-11]。

粒子群優化算法依賴的經驗參數少、操作原理簡單、收斂速度快，能實現局部最優，且收斂精度高。因此，采用該算法可以最大擬合變電站、輸電線路等電力工程的三維數據，進而實現數據的最優化處理[12]。

2 電力工程輸電線路屬性分析

分析電力工程設計中輸電線路的供電路線及供電范圍時，將圖論、GIS 相結合，以各個線路的終端配變作為最小分析對象，構建輸電線路的樹狀屬性：輸電線路是傳輸干道，各T 接線等分接線是分支節點，最終的配電變壓器為終端屬性。基于此，形成輸電線路工程設計的基本模型[13]，如圖1 所示。其中JL為架空線路，DL為電纜線路。

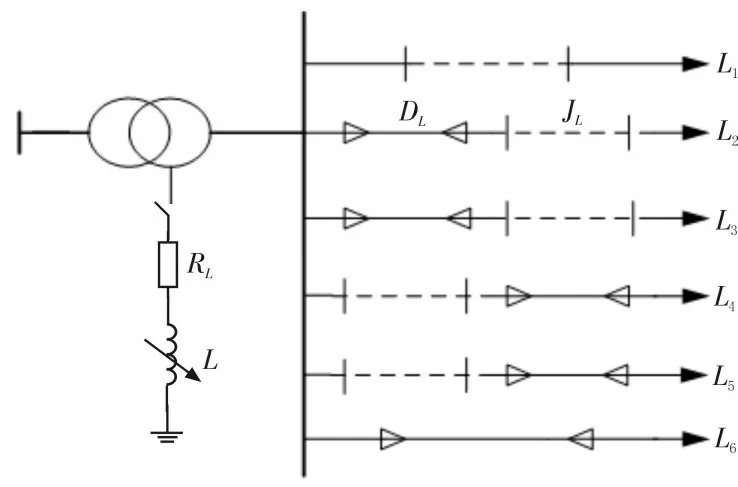
圖1 輸電線路的樹狀屬性關系

圖1 中，供電范圍涉及分析每個線路末端配電與線路長度及走向、T 型線路的供電配合關系，最終還要分析線路與初始供電變電站的關系。先分析線路的供電源，遞推T 接線路與主線路的關系，再研究T 接線路與變電站的潮流負荷轉移屬性。然后，通過整個包絡線主線路、T 接線路、配變、變電站，分析得到合理的電力工程設計方案，確定線路的輸送范圍，從而進行電力工程設計。

3 粒子群算法應用于三維數據處理

3.1 數據預處理

電力工程三維數據是工程設計的原始數據，原始數據易受噪聲影響，難以擬合符合原始特性的數據曲線，必須刨除原始數據的噪聲干擾。文中選用高斯噪聲濾除原始數據中的噪聲因素，平滑原始數據曲線，從而得到有效的原始數據擬合曲線，從根本上消除了噪聲對數據分析的影響，有效去除了符合正態分布特性的噪聲，最終擬合成較好的數據特性曲線，更加符合數據的實際特征。擬合取得數據特征后，更利于后續數據的分析及應用[14]。

高斯核函數表達式為：

曲線的飽和、陡峭程度決定于方差σ。σ值越小，原始數據曲線越陡峭；σ越大，原始數據曲線越平滑。ω表示數據周期，其決定固定周期內原始數據個數的大小，直接決定整體數據的擬合程度。一般地，取σ＜1；ω取單數，且ω≤5。

高斯全局平滑濾波處理的數據結果對比圖如圖2 所示。

圖2 結果表明，經過高斯平滑處理的數據能夠最大程度地、有效地實現數據的擬合處理，最終得到數據的真實特性。

3.2 粒子群算法在數據處理中的應用

適應度函數是粒子群確定全局最優解的關鍵，合適有效的適應度函數能夠使群體搜索中獲得最佳的位置搜索，從而有助于找到最優的數據解。在實際的最優解搜索中，最優化函數用來實現適應度函數功能，通常由式（1）或式（2）構建。

變電站及線路的供電范圍在一定程度上容易受到地理位置、負荷分布等干擾，尤其是多條線路共同構建、共同供電投入時，單一特性的目標函數難以得到最終的最優特性解，對最終的線路供電范圍及線路走向會產生一定的影響。因此，為了獲得準確的線路或變電站選址結果，文中通過引入一個正態分布的度量函數來加以解決，其表達式為[15]：

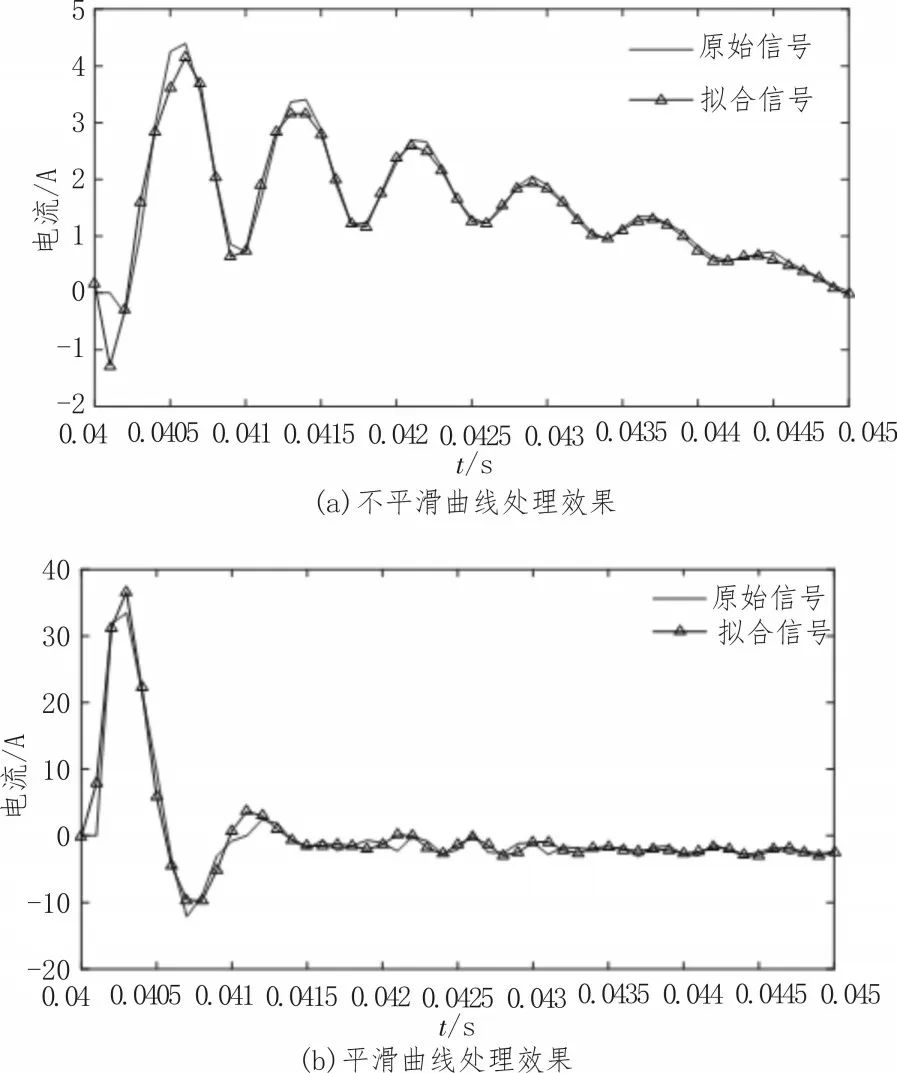
圖2 曲線的高斯平滑處理對比圖

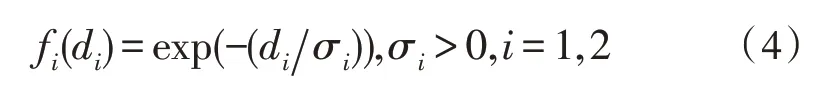
式中，σi表示原始數據的標準差，用來調整原始數據的全局分布。其中，fi(di)值取決于di和σi值的大小。然后，將兩者用乘積特性進行計算，最終得到適應度函數。

從式（4）可以看出，適應度函數值是由di決定的。特別地，當di存在較大數據偏差時，式（4）能糾正單個目標函數分解原始數據特性時的偏差，解決數據搜索方向，從而得到有效、可靠地原始數據特性。

3.3 仿真算例

為顯示粒子群算法的優勢，利用Matlab 進行原始數據優化。Matlab 工具箱可以提供粒子群優化算法，在此基礎上對選用的原始數據進行全局數據處理，按照全局最優解數據的方向得到原始數據的最優解[16]。運用IEEE14 節點系統模擬電力傳輸網絡，如圖3 所示。然后，對數據進行最優解尋找。

在圖3 原始數據結構基礎上，對數據進行最優目標解的搜尋，最終得到最優適應度函數下的最優位置解。

1）如圖3 所示，分別選擇斷開線路4～5、9～10，得到原始數據結構，從而得到數據初值；

2）對原始數據進行初始化處理，設置粒子群各個參數及整個粒子群特征權重值，κ1=1，κ2=1；

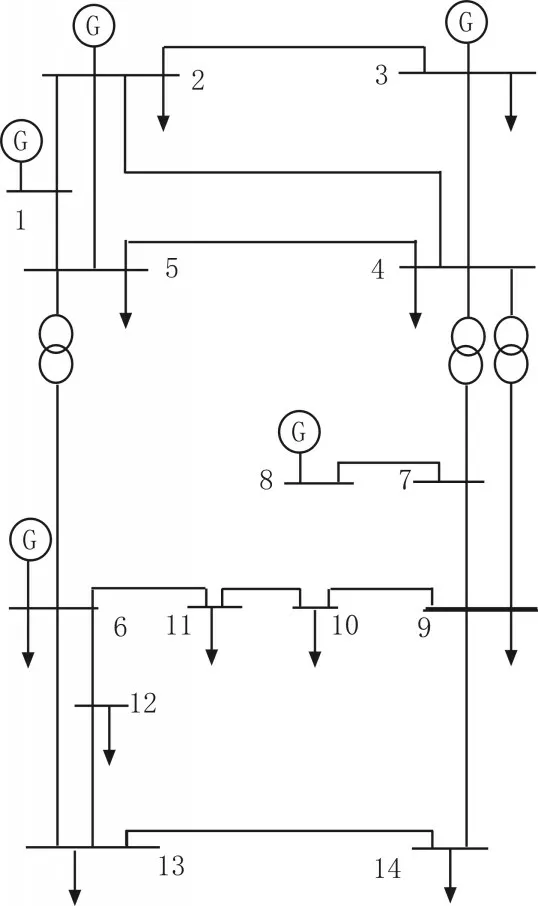
圖3 IEEE14節點系統圖

3）在上述基礎上，找尋最優的適應度函數，從而確定目標函數搜索特性，將特征解計入整體數據范圍，剔除非特征解；

4）確定整體粒子群的適應度，根據各個粒子的空間位置確定最佳的位置解，從而決定搜索方向；

5）根據最佳的搜索方向，確定最佳解的搜索方向及所在位置的半徑；

6）不斷迭代，確定迭代次數，便于快速找尋最佳的局部搜索范圍，如圖4 所示，p2優于p1，魯棒性更強，搜尋位置更佳；

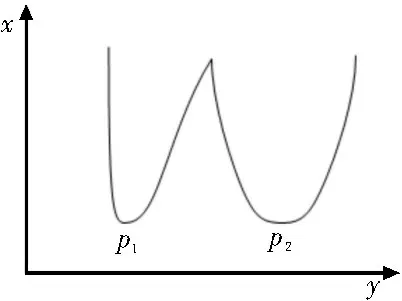
圖4 局部最優范圍

7）分別根據式（1）～（3）更新整個粒子群的速度v和位置x，同時確定整個粒子群各個粒子的最佳位置；

8）根據非特征解確定整體粒子群的非解特性，從而方便得到最佳的位置解；

9）在非特征解中選擇某個個體進行位置篩選，刨除無效的搜索方向，從而找尋最優解的搜索范圍；

10）在一系列的搜索后，確定最終的最優解搜索范圍，然后繼續搜索直至獲得最優解。若條件不滿足，則繼續跳轉步驟3）進行計算。

在上述步驟過程中，由于數據是噪聲處理后的原始數據，將數據結構進行處理，即將斷開線路的系統帶入最優解的找尋流程中。在此基礎上，進一步確定粒子群的最優空間方向，獲得其仿真的原始數據擬合。擬合后的數據在最優目標函數中搜尋最優位置解，刨除非特征范圍。在確定的最優解方向中找尋最優解，最終得到最優位置解。

圖5 數據的迭代結果

其中，對數據的迭代結果如圖5 所示。從該圖可以看出，文中最優化目標函數能夠形成局部解，并進行優化前后對比。優化結果如圖6 所示，圖中橫軸為節點編號，縱軸為相應節點綜測電壓的標幺值。結果表明，粒子群可以較好地擬合數據，得到過濾噪聲后的數據特征。結合實際輸電線路及變電站選址特征，對收集的數據進行粒子群分析整合，從而得到有效的參考數據，最終確定合適的電力工程設計方案。

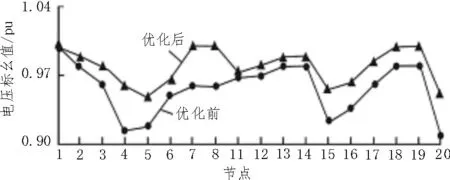
圖6 優化前后系統各節點電壓標幺值

電力工程的原始數據特性容易受到變電站地址、變壓器容量、負荷大小、潮流轉移等因素的干擾，尤其主線路與T 接線路共同劃入電力工程設計中時，單一特性的搜索目標函數難以得到確定、可靠的數據最優解。因此，尋找出最優的目標函數是問題的關鍵。根據上述步驟，能夠找到最優的目標函數，并將噪聲處理后的原始數據代入，從而得到最優位置解。根據最優的位置特征解，研討最終的電力工程設計方案。

4 結論

在電力工程設計中，粒子群算法具有更加優良的特性。該算法可以最大限度地滿足將電力設計中需要采集的實際因素數據進行整合分析，粒子群算法與其他演化算法相比具有快速收斂的能力，能達到局部最優。以地理信息、負荷分布等作為特征，并結合變電站及輸電線路的實際數據進行表征。以此粒子群最優搜索算法的適應度函數為工具，實現多種專業數據的分解，為電力工程設計提供可靠的參考。