基于改進SIFT 的室內全景圖像配準算法研究

王 博，管永紅，劉 洋

（1.中國工程物理研究院流體物理研究所，四川綿陽 621900；2.中國工程物理研究院研究生院，四川綿陽 621900）

圖像配準作為圖像處理中的一項基本問題，用于求解在不同時間、不同探測器、不同角度等所獲取的多幅圖像的最佳的幾何變換，主要應用于圖像拼接、圖像檢索、圖像融合等領域[1-3]。在圖像配準中，圖像特征點提取與匹配又是關鍵的步驟。2004 年Lowe 提出了的SIFT 算法，因其尺度、旋轉等的不變性而被廣泛應用于圖像配準領域[4-5]。但SIFT 算法仍存在一些缺點，研究人員也提出了諸多改進。Bay提出的SUFT 算法通過引入Hessian 矩陣和對積分圖像進行操作來提高速度，但對于邊緣光滑的特征點提取能力較弱[6-7]。韓宇等人提出簡化的SIFT 特征描述子，將矩形區域改為圓形區域來降低描述子的維度[8]。陳抒瑢等人提出Contourlet-SIFT 算法，該算法對尺度不變的特征進行Contourlet 變換，并建立全局紋理描述子，適用于尺度和方向等變換比較明顯的場景[9]。李欽等提出PCA-SIFT 特征匹配算法，對SIFT 特征描述子進行主成分分析,降低了SIFT 特征描述子的維度，從而提高配準速度，但是PCA 算法的引入也增加了計算量[10]。許佳佳等提出基于Harris的SIFT 算法，該算法通過構建尺度空間使得Harris角點具有尺度不變性，并借鑒Forsnters 算子的思想進行角點的精確定位[11]。目前室內全景圖像在室內設計、全景建模等領域有重要應用，而構建室內全景圖像需要對采集到的圖像進行配準。在采集過程中相鄰兩幀圖像較為連續，旋轉角較小，但SIFT 算法的特征點檢測和描述過程較為復雜，計算量較大[12]。為了提高配準效率，文中提出了一種改進的SIFT 算法，通過優化尺度空間的構建過程，引入BRIEF 特征描述子[13]，替換SIFT 特征描述子完成特征點的檢測和描述。實驗證明，改進的SIFT 算法在運算速度和準確率上較原始SIFT 算法都有提高。

1 改進SIFT算法流程

1.1 特征點檢測

圖像的特征點檢測主要包括：尺度空間生成、DOG 圖像生成、尺度空間極值點檢測和定位等步驟[14]。

特征點的檢測需要構建高斯金字塔，SIFT 算法中的高斯金字塔區別于多分辨金字塔。為了體現尺度的連續性，在SIFT 算法中，高斯金字塔不僅需要簡單的下采樣，高斯濾波也用于生成多尺度圖像。最后，一幅圖像可以產生若干組圖像，而一組圖像包括多層圖像。

高斯拉普拉斯(LOG) 算子是一種二階導數算子，在特征檢測中有廣泛的應用[15]。LOG 算子首先計算圖像的二階微分，后通過檢測二階微分的零點來識別目標邊緣。LOG 算子的表達式如式（1）所示：

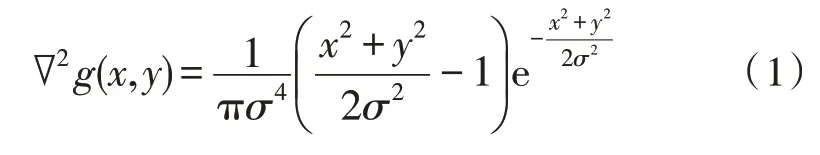
通過在相鄰的高斯空間中對一定尺度的圖像進行特征相減，可以獲得DOG 響應值圖像D(x,y,σ)，DOG 的表達式計算公式如式（2）所示：為了在尺度空間中完成極值點的搜索，需要將每個采樣點與周圍的8 個點、上下尺度的9 個點，一共是26 個點進行比較[16]。

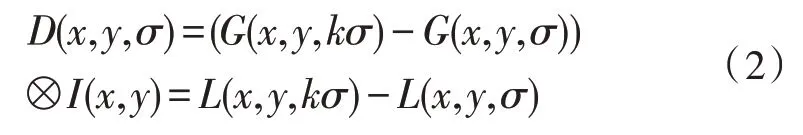
上述極值點的檢測過程是在離散空間中完成的，因此檢測到的有可能并不是真正的極值點，為了使得到的極值點更加精確，通常會使用子像元插值法得到連續空間的極值點[17]。

因DOG 對圖像的邊緣有很強的響應，如果特征點落在了邊緣點上就會變成一個不穩定的點，為了獲得穩定的點，需要對落在邊緣上的特征點進行剔除。邊緣點的剔除需要計算局部極值點所在位置和尺度的Hessian 矩陣。Hessian 矩陣可表示為：

計算得到Hessian 矩陣的兩個特征值λ1和λ2(假設λ1＞λ2)，如果λ1?λ2，則說明該特征點為邊緣點。Hessian 矩陣的跡和行列式表達式如式（4）～（5）所示：

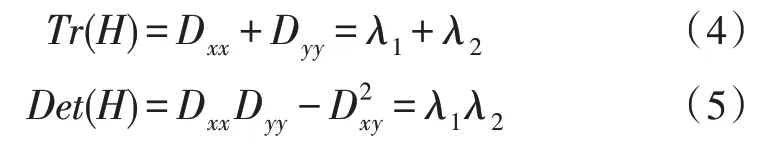
因為計算特征值的過程比較耗時，為了規避該過程，根據Hessian 矩陣的跡等于Hessian 矩陣的兩個特征值的和，Hessian 矩陣的行列式等于兩個特征值的乘積這兩個結論，令r=λ1/λ2，則有：

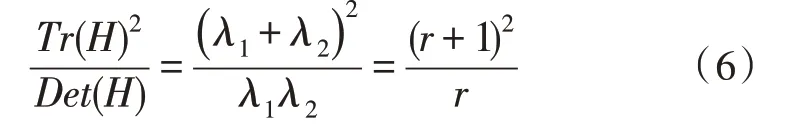
由式（6）可知，結果只與兩個特征值的比值r有關系，當式（6）的比值比較大的時候，說明該點為邊緣點。因此，只需要設置閾值與式（6）的結果進行比較即可篩選出邊緣點。

在SIFT 算法中，構造了4 層Octave 來進行特征點的檢測以適應更大的尺度變化。雖然4 層Octave可以適應更大的尺度變換，但在提高算法魯棒性的同時也增加了構建尺度空間和檢測特征點的時間。在室內全景圖像配準的場景中，相鄰幀圖像的尺度變化、旋轉、縮放等較小，為了提高配準效率，文中統計了室內圖像不同尺度的特征點數目和提取這些特征點需要的時間，統計結果如表1、表2 所示。

其中，測試的數據來自用于評估圖像對齊方法的PASSTA 數據集。通過表1 和表2 可知，在室內圖像構建的第3、4 個Octave 中僅僅提取出少量特征點，但是卻造成了極大的時間損耗。為了提高室內全景圖像配準效率，文中拋棄提取特征點較少的最后兩個Octave，僅利用提取特征點較多的前兩個Octave 完成特征點的檢測，改進的圖像Octave 如圖1所示。

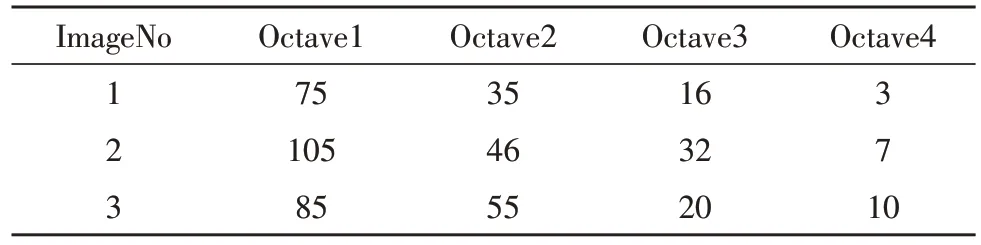
表1 不同Octave提取特征點個數統計

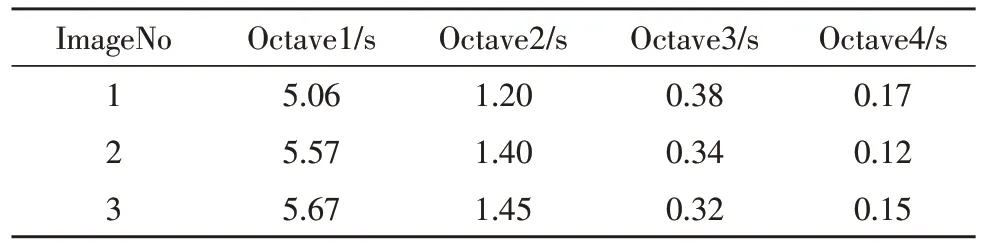
表2 不同Octave提取特征點和計算描述子時間統計

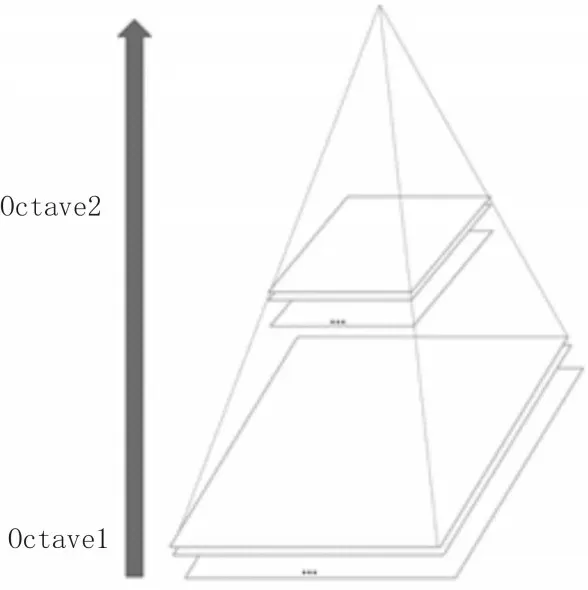
圖1 改進的圖像Octave

1.2 特征點描述

在原始SIFT 算法中得到特征點之后，應當對特征點進行描述。首先，需要對特征點的鄰域做直方圖統計[18]，直方圖的橫坐標將0°到360°以10°為間隔平均分成36 份，直方圖的列代表梯度方向的累加值。為了使特征點具有旋轉不變性，計算SIFT 特征描述子時需要將區域旋轉至主方向，而主方向即直方圖峰值對應的角度。將區域劃分成4 × 4 個子區域，在每個子區域內使用8 方向的梯度直方圖進行統計[16,19]，圖2 所示為特征點描述的示意圖。因此，形成了128 個的描述子，這128 個特征描述子就是SIFT 描述子。最后，再進行歸一化以消除光照的影響，得到了最終的SIFT 特征描述子。

SIFT 特征描述子具有較高的抽象特征能力，因此，對圖像旋轉有很強的適應性，但這也提高了特征點描述子的計算復雜度和匹配的復雜度。在室內全景圖像的配準中，由于圖像拍攝較連續，旋轉角度較小，不需要用較為復雜的特征描述子描述，因此，采用較為簡潔的BRIEF 特征描述子來代替SIFT 的特征描述子。

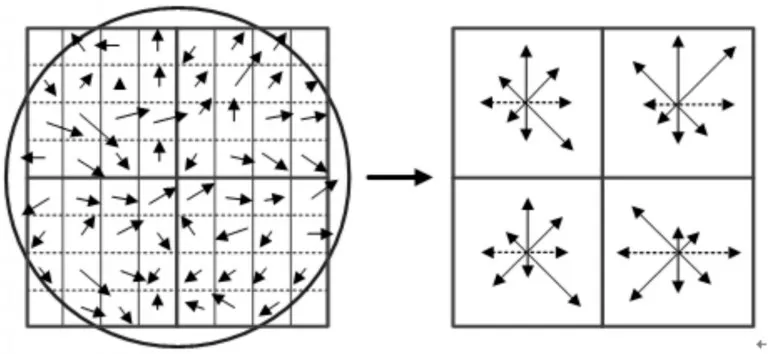
圖2 SIFT特征描述子

BRIEF 特征描述子提供了一種計算二值化特征描述子的方法，如圖3 所示。BRIEF 特征描述子在特征點周圍選擇一個區域，在區域中挑選出來n個點對，對于每一個點對(p,q)，比較這兩個點的亮度值，如果I(p)＞I(q)，則這個點對生成的描述符中的值為1，否則為0。完成n個點對的計算之后，就會生成一個二進制串的特征描述子。BRIEF 特征描述子相對于SIFT 特征描述子而言，只有0 和1 兩個值，不僅簡化了特征描述子的計算過程，同時也簡化了后續特征點的匹配計算流程。

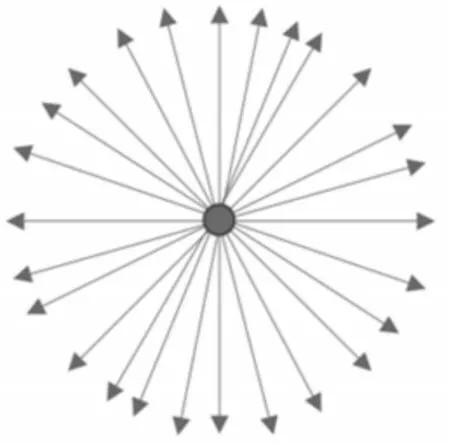
圖3 BRIEF特征描述子

為了證明改進特征描述子的有效性，文中針對3 幅室內圖像的前兩個Octave，統計SIFT 特征描述子和BRIEF 特征描述子所耗費的時間，統計結果如表3 所示。

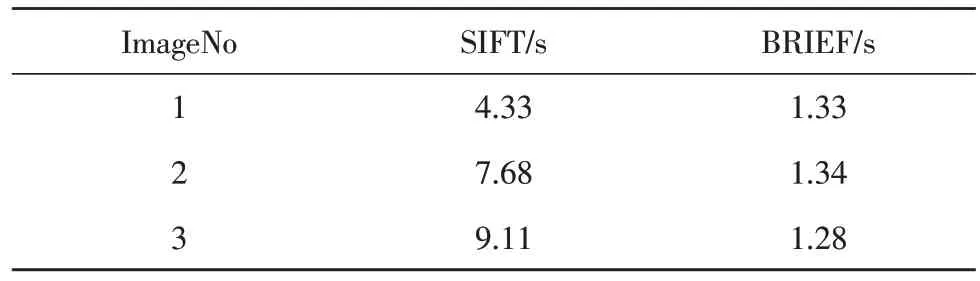
表3 SIFT和BRIEF計算耗時統計

1.3 特征點匹配

完成了對室內圖像的特征點檢測和描述之后，首先，需要對兩幅室內圖像生成的特征點進行匹配，從左室內圖像中循環獲取特征點，針對左圖中的每一個特征點，在右圖中匹配與之對應的特征點。匹配過程使用KNN 算法，為每個特征點返回匹配的兩個點，在這兩個特征點中，當最近的距離與次近的距離的比率小于0.75 時，認為這兩個點是一對匹配點。

2 實驗結果分析

為了證明改進SIFT 算法的有效性，文中進行了必要的對比實驗。實驗均在MacBook Pro (13-inch,2018,Four Thunderbolt 3 Ports)上進行。處理器為2.3 GHz Intel Core i5,內 存8 GB。編 程 環 境 為Python3.6。采用PASSTA 數據集作為原始數據來檢驗圖像配準效果。通過實驗，對比改進SIFT 算法與原始SIFT 算法在配準準確率、配準點對個數和配準時間上區別。其中，配準精度計算公式如式（7）所示：

其中，TP表示正確配準的點對數，FP表示錯誤被匹配到的點對數，P表示配準精度。配準時間是兩幅圖像從特征點檢測到完成最終的圖像配準所消耗的總時間。

圖4 為從數據集中挑選的待配準的兩幅室內圖像，圖像大小為456*684。圖5 為使用原始SIFT 算法后得到的配準圖像，圖6 為使用改進的SIFT 算法得到的配準圖像。

圖4 待配準圖像

圖5 SIFT算法配準結果

圖6 改進SIFT算法配準結果

統計配準精度、配準點個數以及配準時間如表4所示。

表4 實驗結果對比

3 結論

文中提出了一種改進SIFT 的室內全景圖像配準算法，提取特征點的過程中通過改變高斯金字塔的結構進行快速特征點提取。此外，在特征點描述時使用了BRIEF 特征描述子來代替SIFT 特征描述子，并使用KNN 算法完成特征點的匹配，最終高效的完成了室內全景圖像配準工作。實驗結果表明，在室內全景圖像的配準任務中，該算法較原始SIFT算法，大大縮短了配準時間，并提高了配準準確率，可以高效的完成室內全景圖像的配準任務。