模態質量參數測試方法研究

楊正璽，常洪振

(1.北京機電工程研究所，北京100074；2.北京強度環境研究所，北京100076)

0 引言

結構動力學方程包括結構的質量矩陣、剛度矩陣和阻尼矩陣。其中,質量矩陣儲存著結構各部分的動能,剛度矩陣存儲著結構各部分的勢能,阻尼矩陣則代表能量在結構的各部分之間的轉移(例如機械能轉化為內能),結構的總能量通過這三個矩陣進行相互轉換,由此形成結構持續的運動(振動),結構共振時的形態,稱之為模態。

結構動力學中的模態對應實際物理意義上的振動形態,在數學意義上則對應非齊次微分方程的特征值問題。結構動力學模型對應的方程在物理坐標系下,質量矩陣和剛度矩陣均是非對角的對稱正定矩陣,若直接求解方程難度較大。通常的做法是,借助模態向量基的正交性將結構實際的非對角質量矩陣和剛度矩陣轉換為對角矩陣,這樣就可以將結構在物理坐標系下的多自由度系統解耦為n個單自由度組成的系統,由此方程求解可大為簡化。上述解耦過程得到的模態坐標系下的對角質量矩陣和剛度矩陣就稱為模態質量陣、模態剛度陣,每個對角元素稱為結構該階模態質量、模態剛度。

模態質量和模態剛度是為了數學計算的方便在模態坐標系下的定義,不再具有實際的物理意義和量綱。不過由于其也是對實際結構的一種描述,在模態坐標系下得到的這些參數也可通過廣義反變換的方式轉化為實際物理系下的力學參量[1],即具有實際物理意義。例如在航空航天領域可利用模態質量和模態振型參數來計算飛行器飛行過程的結構動力學方程系數以及動載荷,為控制系統的設計和載荷環境條件的設計提供重要依據[2-5]。由此看來,模態質量和模態剛度等動特性參數在航空航天領域的結構動力學設計中占據著重要的地位。基于此,一些學者已經提出基于有限元模型獲取模態質量和模態剛度的方法[6-9],但該方法的測試結果極依賴于所建立有限元模型精度,對于一些復雜結構的完整的有限模型難以建立,因此該方法有很大局限性。由于模態質量和模態剛度可以通過結構固有頻率相互導出,本文僅研究模態質量獲取方法,其中重點研究試驗測試方法。

1 公式法

根據定義,模態質量矩陣等于結構物理坐標系下真實的質量矩陣左乘模態振型矩陣的轉置,右乘模態振型矩陣為

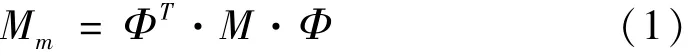
式中:Mm為模態質量矩陣;M為物理坐標系下真實的質量矩陣;Φ為模態振型;ΦT為模態振型矩陣的轉置。

式(1)中,需已知結構物理坐標系下真實質量矩陣,對于復雜結構,需先建立有限元模型,物理坐標系下真實質量矩陣、模態振型均可通過有限元模型提取。考慮到有限元模型與結構相比有一定誤差,獲取的模態振型也會有誤差,并且直接通過完整的有限元模型提取的參數容量一般較大,不便于直接計算。工程中通常使用的方法是利用試驗實測振型數據和有限元模型提取的物理坐標系下真實質量矩陣配合進行計算,公式中的模態振型矩陣由試驗來給出,真實質量矩陣通過有限元模型縮聚到試驗測點處的縮聚模型給出,這樣就極大減少計算量,同時提高結果的準確性,但該方法仍需要建立結構的有限元計算模型,因此,該方法對于復雜結構存在一定使用局限性。

2 基于頻響函數的試驗方法

2.1 方法原理

根據模態理論,在比例粘性阻尼假設下,n自由度系統用模態參數表示的加速度頻響函數矩陣為

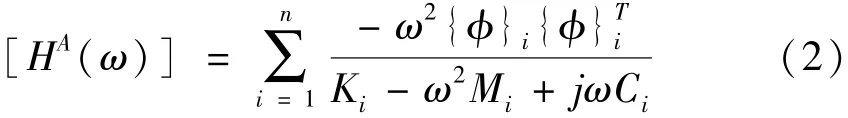
式中:ω為固有頻率;{φ}i為第i階模態的振型為第i階模態振型的轉置;Mi為模態質量;Ki為模態剛度;Ci為阻尼系數。

簡單的單點激振情況下,上述矩陣的第l行第p列分量即在p點激振,l點測量的加速度傳遞函數為

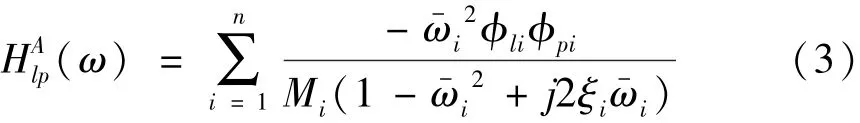
上述頻響函數式子包含了各階模態參數,對于一般的小阻尼系統,若在模態密度不是很高、相鄰模態相互影響不大的情況下,式(3)可簡化為

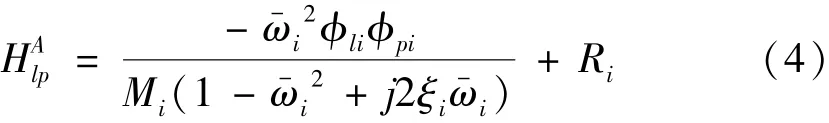
式中:Ri為復常數,表示第i階以外其他各階模態影響總和。

將式(4)的實部和虛部分開

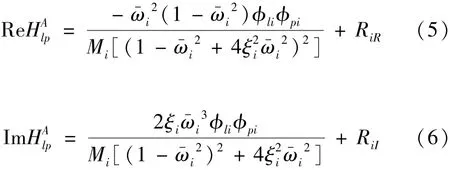
當Ri=0時,根據式(5)和式(6)繪制實頻、虛頻曲線;當Ri≠0,曲線將上移RiR和RiI。這時可直接由圖解識別法快速檢索求得模態參數,分別確定該階模態的固有頻率ωi和模態阻尼比ξi。

2.2 錘擊法

若試驗采用錘擊法,振型測量可由頻響函數矩陣中一行的虛部峰值得到。若將余項Ri當做小量忽略,再令即在共振頻率處,則由式可得傳遞函數虛部峰值點的值為

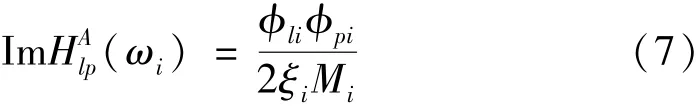
錘擊法為響應點l固定,激振點p=1,2,3…n時,令其中m點為歸一化參考點,即φmi=1,參考點m的頻響函數虛部峰值為

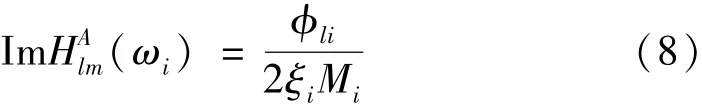
第p點的歸一化后振型為

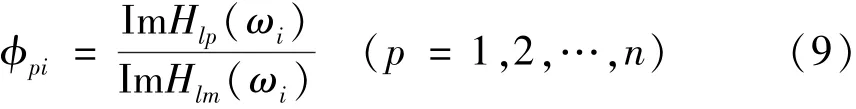
整理可得錘擊法中該階模態質量計算公式為

當響應點與歸一化點一致時,模態質量計算公式為

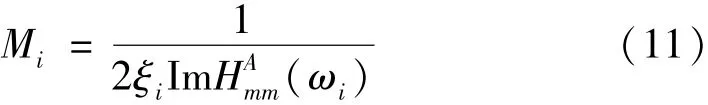
2.2 激振器法

若試驗采用激振器法,推導過程與錘擊法類似,激振器法中模態質量計算公式為

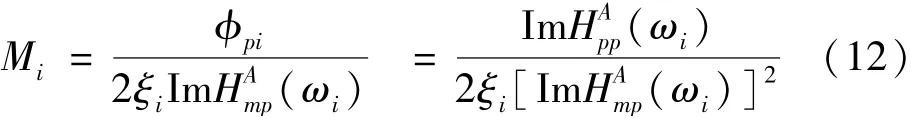
當激振點與歸一化點一致時,計算公式(12)與式(11)一致。

2.3 模態質量的修正

由式(10)～(12)可以看到,模態質量的測試精度直接取決于阻尼比ξ和頻響函數H的測量精度。對于阻尼比的精度,影響因素主要包括各階模態的分離程度、測試中所使用窗函數以及測試設備本身的頻率分辨力。在測試中可通過優化激振位置盡量使各階模態分離,使分析頻段內僅為單一模態,以提高阻尼比識別的準確性。對于測試設備的頻率分辨力則要求每次測試分析頻率上限值根據各階模態頻率分別設定,并且盡可能選擇低的上限。

頻響函數是有量綱的,雖然試驗系統中的力和加速度傳感器一般都要求使用提供的靈敏度標定值,但通常計量部門所做的標定是在靜載下或特定頻率下的。頻響函數測試是一個動態過程,頻率范圍廣,傳感器靈敏度將會發生變化,特別對于力傳感器,錘擊法中所測得的力值是錘頭和傳感器之間的力,并不是直接作用于結構上的力,它與所使用力錘的重量、錘頭以及結構的材質都有關[10-11]。為保證頻響函數測試的準確度,測試前需要先對所用的測試設備作組合動態標定。

通常采用文獻中介紹的標準質量塊絕對標定法。如圖1所示,標定過程所使用的測試系統與模態測試系統相同,只是將結構試驗件改換為標準質量塊或砝碼。

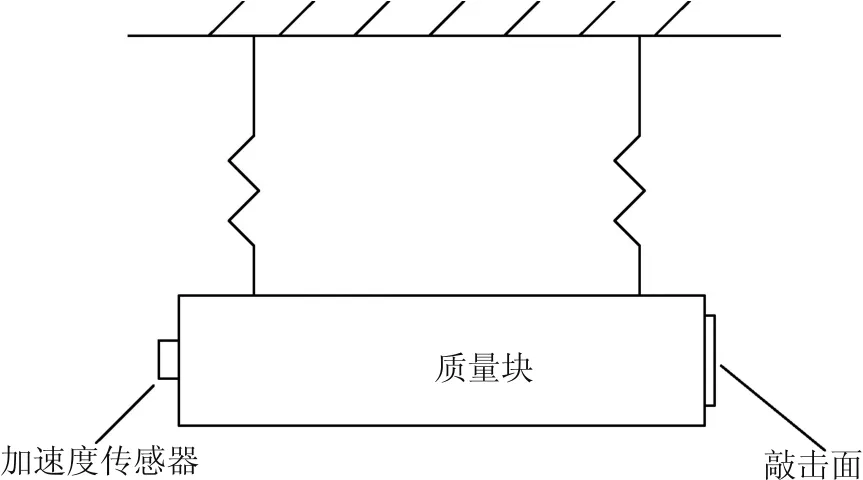
圖1 修正方法示意圖

將砝碼用橡膠繩懸吊起來,在砝碼的一個端面中心粘貼加速度傳感器,另一端面中心作為錘擊點或激振點,在錘擊點或激振點位置粘貼一片與實際結構相同的材料。標定過程的分析儀頻率上限取模態測試時可能采用的最高頻率,窗函數甚至指標都應與模態測試時相同,會對標定結果產生較大影響。標定過程與模態測試相同也取多次測試平均,次數可適當增加。標定結果曲線為一條有小幅波動的水平直線,可在所標定的頻率范圍內取若干點的平均值作為最終標定值。根據牛頓第二定律,質量為m的砝碼,自身頻率足夠高,在所標定的頻率范圍內,其頻響函數應與靜態時一致,為1/m,故系統的標定系數可寫為

模態試驗直接測得的頻響函數值H試,可由式(13)修正為實際的頻響函數值

將式(14)代入式(10)和(12),可得模態質量的修正結果。

3 基于頻率變化率的試驗方法

上述基于頻響函數的試驗法存在不足:一是要測定準確的阻尼比值,對于密集模態情況需要多次優化激振位置,工作量大且效果有限,阻尼比的準確度難以保證;二是測定準確的激振力和響應的幅值,要求傳感器和測量儀器有準確的靈敏度標定值,傳感器和測量儀器通常僅在計量部門所做的靜載或特定頻率下的標定值是不夠的,需要在模態測試前對實際使用的測量系統作組合動態標定,較為繁瑣。本節所介紹的基于頻率變化率的試驗方法不需要測量力幅和振幅的絕對值,避免了標定程序,更為簡便可靠。

首先使試件處于某階模態共振點,然后在試件上一點或若干點上逐級增附加質量,改變激振頻率,重新建立共振,測量相應的共振頻率移動量即可確定模態質量。假設附加質量后試件振型不變,則模態剛度也不變,即

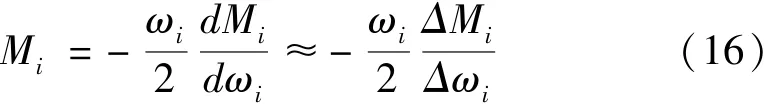
對ωi求導可得

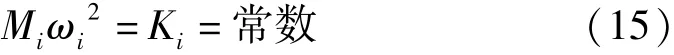
式中:ΔMi為各點附加質量mp與對應的p點規格化振型平方乘積的總和。

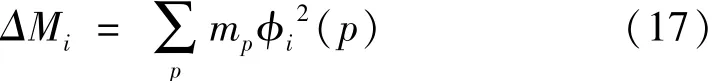
為避免偶然誤差影響,提高測試準確度,可繪制一條質量變化-頻率變化曲線,取得曲線起始點附近的斜率值,將其代入公式中計算模態質量。

由于該方法假設附加質量后試件振型不變,即模態剛度不變,因此附加質量的大小不應過大,參考飛行器相關模態試驗標準[12]中對于邊界支承工裝所產生的附加質量要求的規定,本文定性給出該方法中附加質量的大小應小于試驗件質量的1%,供使用中參考。

4 應用實例

采用梁結構進行試驗測試方法驗證,尺寸為長1500 mm×寬100 mm×厚3 mm,模態質量以右端部所在位置歸一化,主要考慮梁的前三階模態。首先建立有限元模型以利用公式法計算模態質量,并以此結果作為評定試驗方法獲取結果的基準。

進行錘擊法自由模態試驗,在右端部和中間位置布置兩個響應測點,變換錘擊點進行模態測量,梁結構實物如圖2,有限無模型圖3所示。

圖2 梁結構實物圖

圖3 梁結構有限元模型

重點獲取準確的傳遞函數曲線并識別模態阻尼比參數,并利用砝碼對傳感器和測試系統進行聯合標定,如圖4利用錘擊方法計算模態質量。

圖4 傳感器和測試系統的聯合標定

重新進行錘擊法自由模態試驗,在右端部即歸一化點處逐級粘結不同質量的砝碼(如圖5),然后重新測量結構的共振頻率,利用第3節介紹的方法作出質量變化-頻率變化曲線,如圖6所示,取得曲線起始點附近的斜率值代入第3節公式中,計算模態質量。

圖5 梁結構上附加不同質量的砝碼

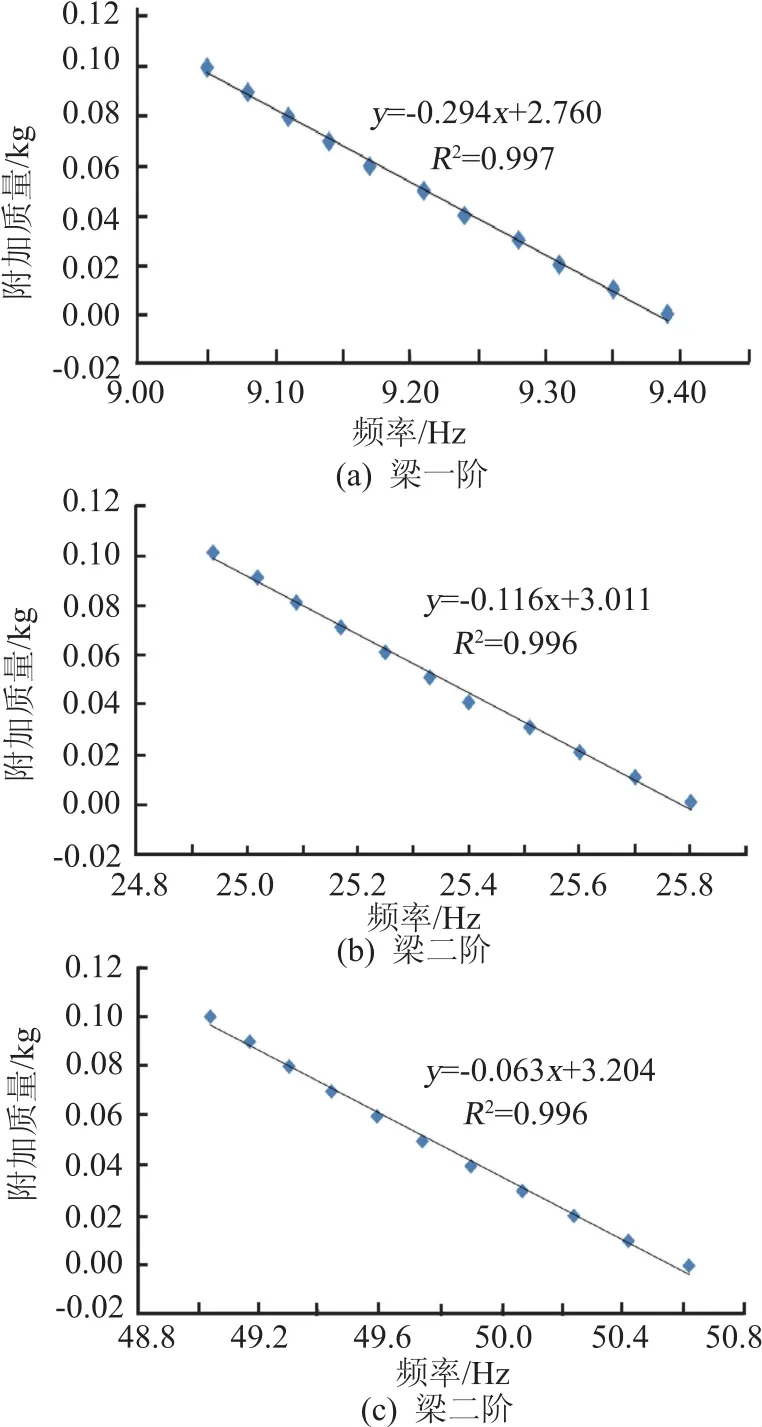
圖6 模態質量變化-頻率變化曲線

兩種試驗方法得到的梁前三階模態質量結果與公式法計算的基準的對比(括號內為誤差百分比)見表1所示。

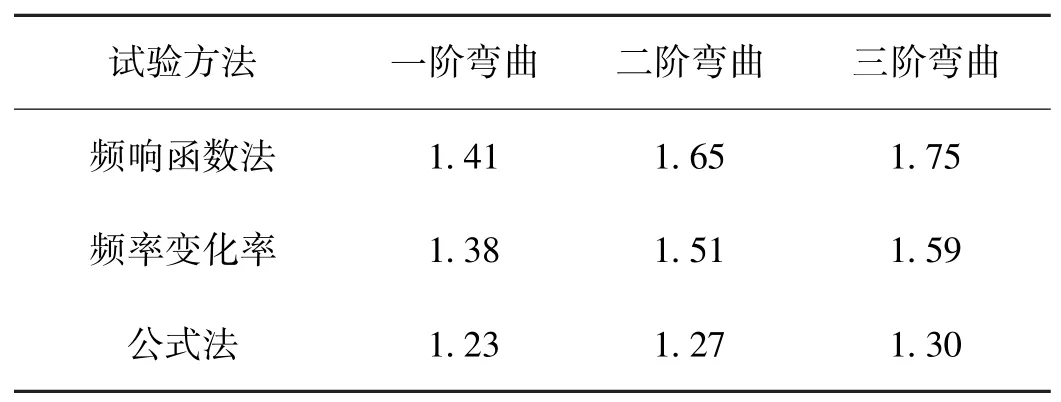
表1 兩種測試方法與公式計算基準結果對比

由表可知,頻響函數法得到的結果除一階模態誤差為15%外,二階、三階結果誤差為30%,35%,誤差較大;基于頻率變化率的試驗方法得到的結果各階模態誤差均可控制在20%左右,能夠滿足實際工程的需要。

5 結論

基于有限元模型的公式法獲取模態質量在工程中僅局限于簡單結構的使用,本文對基于頻響函數、頻率變化率獲取模態質量參數的試驗測試方法進行了研究,并應用于實際梁結構,對兩種試驗測試方法獲得的結果與公式法計算的基準結果進行對比,表明基于頻率變化率的試驗方法得到的結果誤差可控制在20%左右,能夠滿足實際工程的需要,為獲取復雜結構模態質量參數提供了可行的方法。