水煤漿粒度級配模型和實踐的研究進展

李 強，廖長林，侯 健，張建勝

(清華大學 能源與動力工程系 熱科學與動力工程教育部重點實驗室，北京 100084)

0 引 言

我國石油天然氣儲量少，且對外依存度不斷加大，煤炭儲量相對豐富，煤炭依然是我國的基礎能源[1-2]，短期內難以被全面替代[3]。要解決煤炭利用中產生的污染問題，關鍵要推進煤炭清潔高效利用[4-5]。煤氣化技術作為煤炭清潔高效利用的重要組成部分和煤化工的龍頭技術，在化工、煉油、電力以及冶金等行業具有廣泛的應用[6]。目前工業化和大型化的煤氣化工藝以氣流床煤氣化爐為主，從進料方式上可分為干法(煤粉進料)和濕法(水煤漿進料)。煤粉進料氣化目前在國內應用較多的主要有Shell、GSP和航天爐等；水煤漿進料氣化目前主要是GE、四噴嘴和清華爐(晉華爐)等[7]。水煤漿是一種重要的煤氣化原料和液體燃料，在煤氣化產業中，從煤消耗量方面統計，我國一半以上的煤氣化裝置采用水煤漿進料。據不完全統計，目前我國水煤漿使用量已超過2.5億t/a[8-9]。

水煤漿是一種煤基液態燃料，具有與燃料油相似的物理特性，是煤炭高效清潔利用的重要途徑，可顯著減少NOx和SO2排放。長期以來，煉焦煤等高階煤制漿性能較好，但焦煤儲量低、價格高，已無法滿足水煤漿產業快速發展的需要[10]。新疆、內蒙古和陜西等地具有豐富的低階煤儲量，且價格低，不僅能以低廉的價格保證水煤漿用煤的持續供應，提高經濟性，同時又符合國家煤炭梯級利用和節能減排的政策[11]。但低階煤水分高、可磨性較差，制備的水煤漿濃度偏低(45%～55%)，極大影響水煤漿的氣化與燃燒效率。以60%的水煤漿進料、1 500 t/d處理量的氣化爐為例，按效率粗略估算，若煤漿濃度降低1%，每年需多消耗4 000 t煤[12]；對于熱值25 GJ/kg的原料煤，在55%的水煤漿、4 MPa和1 350 ℃條件下，若將水煤漿中煤濃度提高5%，可多產合成氣5%，減少氧氣消耗7%[13]。

粒度級配作為水煤漿濃度的3個重要影響因素(煤質、粒度級配、添加劑)之一，是決定水煤漿流變性和穩定性的重要因素。為保證水煤漿在燃燒或氣化過程中的高效率，水煤漿粒徑應小于30 μm， 74 μm以下的顆粒含量應大于75%[14]。同時還要求具有良好的粒度分布，使不同大小的煤顆粒互相填充，盡可能減少空隙，提高顆粒的堆積效率和水煤漿濃度。因此，粒度級配技術是提高低階煤成漿濃度的有效途徑。

本文分析了粒度級配對水煤漿的影響，指出在水煤漿制漿過程中，粒度級配只涉及物理破碎和研磨，能耗相對較小，對于濃度的提升效果顯著，具有廣泛的適用性和經濟性；論述了近年來新發展的粒度級配理論和模型，給出了具體的計算方法和公式，以及假設和適用性。通過舉例論述近年來粒度級配理論的應用及在工業生產中的實踐和效果；最后提出粒度級配進一步發展的建議和展望。

1 粒度級配對水煤漿的影響

1.1 影響水煤漿濃度的主要因素

水煤漿濃度的影響因素主要有煤的理化性質、粒度分布和添加劑。煤的理化性質包括煤的變質程度、化學組成(內在水分、含氧官能團、礦物組成等)、孔結構(平均孔半徑、比表面積、孔容等)和表面特性(疏水性、zeta電勢等)[15]。煤的理化性質中，平衡水分是影響煤成漿性的主要參數之一。在具有相同體積分數煤顆粒的水煤漿中，煤內部的平衡水分越多，意味著更少的干燥固體(或熱值)添加到水煤漿燃料中。煤的親水性越強，其表面和內部吸附的水越多，使水煤漿濃度降低[15]。無煙煤由于缺乏揮發性物質，反應性較低，導致點火穩定性差，因此一般不適合制造水煤漿[16-17]。除無煙煤外，高階煤表面具有疏水性，易形成高濃度水煤漿。低階煤(如褐煤)含有大量親水的氧官能團，通常低階煤制成的水煤漿成漿濃度小于60%，但低階煤水煤漿具有不凝聚、穩定性好和高反應性的優點[18-19]。

水煤漿添加劑主要分為分散劑和穩定劑。分散劑一般是表面活性劑，附著在煤顆粒表面，防止顆粒團聚，促使煤顆粒在水中均勻分散，以提高水煤漿濃度。常見的分散劑有萘系、木質素系、腐植酸系、氨基磺酸鹽系、聚羧酸系和脂肪族。穩定劑一般用于改善水煤漿穩定性，部分穩定劑通過產生疏松團聚結構(“軟沉淀”)，防止顆粒沉降或形成“硬沉淀”。常見的穩定劑有高聚物類(羧甲基纖維素、聚丙烯酸鹽等)和高價陽離子鹽類。不同煤種，對于不同添加劑的敏感度不同，即一種分散劑對于某種煤可顯著提高其制漿濃度，但對于另一種煤，或許不明顯，甚至會降低其制漿濃度。有時分散劑和穩定劑的作用相反，說明其發揮作用的應用場景不同：穩定劑通常用于水煤漿儲存，剪切速率低；分散劑通常用于水煤漿輸運和霧化，剪切速率相對較高。因此，分散劑和穩定劑之間存在協同效應，需根據具體煤種設計。有學者[20-22]在水煤漿中添加第二流體、第二顆粒，取得了一些研究成果，如將第2種不與懸浮液連續相混溶的流體(如煤油)加入干燥的褐煤顆粒中，在煤表面形成薄的疏水膜；將疏水性好的第二顆粒分散在第二流體中，加入褐煤水煤漿中。結果表明，加入第二流體后，褐煤水煤漿表觀黏度降低；加入第二顆粒后，黏度進一步降低，主要是因為增加了褐煤表面疏水性。

對于低階煤(如褐煤)，自身含水量高(部分維多利亞褐煤的含水量超過60%)，其制成的水煤漿濃度低于55%[23]。因此人工改變煤的理化性質提升煤階是一個研究方向，可降低含水量，生產高熱值煤，并降低與褐煤有關的運輸成本。常用的脫水技術有機械熱壓法、水熱法、蒸汽流化床干燥法和微波干燥法等[24-25]，這些方法均涉及物理和化學反應過程，能耗較高，經濟性有待進一步提高，缺少廣泛的應用性。在制漿過程中添加分散劑和穩定劑，約占煤干基質量的1%或更少。添加劑可增加煤的成漿濃度，但成本較高，且缺少煤種的廣泛適用性。在水煤漿制漿過程中，粒度級配應用廣泛，因為只涉及物理破碎和研磨過程，粒度級配能耗相對較小，而提升濃度的效果顯著，具有廣泛的適用性和經濟性。

1.2 粒度級配對水煤漿濃度的影響

顆粒粒度分布是決定水煤漿制漿濃度以及流變特性的主要因素之一。粒度級配變化不僅影響其煤種的成漿性，同時影響其流動性和穩定性[26]。一般來說，在粒度分布上采用雙峰或多峰級配來提高煤顆粒的堆積密度，進而提高水煤漿濃度[27-28]。較細的煤顆粒填充到較大的煤顆粒空隙中，形成更高的濃度填充體系，減少空隙吸收的水分，使加入的水盡可能多的以“自由水”形式存在，并起潤滑作用，從而降低水煤漿的表觀黏度，提高可制漿的最大濃度。

在粒度級配時，首先要考慮磨煤方式和研磨流程，近年來，三峰級配制水煤漿技術在工業上有較多應用，其通過在傳統單棒磨機的基礎上添加了細磨機和超級磨機，按照一定回流配比，在大顆粒間填充了平均粒徑30 μm細顆粒和5 μm超細顆粒，使大小顆粒相互填充，實現了煤漿顆粒的三峰級配(圖1)，提高了煤漿堆積效率。相較于傳統技術，三峰級配可提高水煤漿濃度2%～5%[29-33]。分級研磨技術也是工業上應用較多的新技術，可有效提高水煤漿中煤顆粒堆積效率，同時提高研磨效率[34-37]。該技術將選擇性粗磨與超細磨機進行有機組合，優化煤漿的粒度級配，與常規單磨機制漿工藝相比，煤漿質量分數可提高2%～4%。

圖1 三峰級配中顆粒堆積狀態示意[30]

2個技術的關鍵是引入超細磨機和增加粒度分級，通過控制回流比例以合理配置各分級粒度的比例，使粒度級配更合理，制造更高的堆積效率，增加制漿濃度。主要區別在于：① 在最終粒度上，分級研磨為近似雙峰級配，而三峰級配為3種粒度級配，其最小一級粒度約為6 μm，比雙峰級配的粒度更小；② 磨煤設備上，分級級配在粗磨機的基礎上，增加了超細磨機和配套設備，而三峰級配在粗磨機的基礎上，增加了細磨機和超細磨機，實現3種粒度的研磨。在設備投資方面，運營成本和煤漿濃度各有優劣，總體上均可有效提高水煤漿濃度。

近年來，新的理論和方法在粒度級配分析過程中得到了廣泛應用，使煤粉堆積方式更優化，提高了水煤漿濃度。王俊哲等[38-39]利用分形理論，研究煤粉粒度及顆粒級配技術，通過優化細粉級配，使煤粉粒度實際分布更接近理論模型的理想分布，大幅改善了神府煤粉成漿性。Yang等[14]基于分形理論，提出了一種改進褐煤水漿填料狀態的二級分形模型，結果表明，褐煤顆粒體系的堆積效率主要由74 μm以下顆粒的分形特性決定，分形維數在2.6～2.7，可顯著改善充填狀，當粗、細、超細3種不同分級的顆粒比例為7∶0∶3 時，堆積效率最高，可增加2.9%的成漿濃度。

1.3 內在水分對粒度級配和水煤漿濃度的影響

在粒度級配理論中，水煤漿黏度隨煤顆粒體積分數的增加而增加，由此提出最大堆積密度概念，對于某種煤，若其單峰粒度分布水煤漿體積分數為65%時，黏度非常大，且快速上升；而理想化的多峰級配可理論上生成體積分數大于80%的水煤漿[28]。

由于高階煤和低階煤內在水不同，在計算煤顆粒最大填充體積分數時，也需考慮內在水分，從質量分數轉換成體積分數的方法也不同。對于高階煤，可假設煤顆粒干燥，并忽略煤中水分。通過將煤質量(mcoal)除以其密度(ρcoal)計算體積，因此，高階煤制得的水煤漿體積分數(φ)的計算公式為

(1)

式中，m(H2O)為水煤漿配制時加入水的質量；ρ(H2O)為水的密度。

低階煤(如褐煤)具有多孔結構和親水表面，含有大量水分，計算體積分數時應考慮內在水分，其計算公式為

(2)

式中，ρlignite為低階煤密度；ahum為煤的平衡水分，即煤接近100%相對濕度時的內部水分，一般從試驗得到。

由于內在水分的存在，對于不同煤階的煤種，雖然通過粒度級配均可達到很高的填充效率和堆積體積，但最終的黏度和最大成漿濃度不同[40]。對于同一種煤，填充效率越高，黏度越小，粒度級配提升制漿濃度的效果越顯著。

2 粒度級配理論和模型

2.1 粒度的表征和分布

粒度級配的關鍵是提高顆粒的堆積效率，在一定空間內使顆粒占據更多的體積，需要具體的理論來指導和設計粒徑分布，提高堆積效率，即提高固體顆粒在有限空間內的體積分數。首先必須將顆粒分布進行函數化表達。

在實際水煤漿生產過程中，采用磨礦設備制得的煤粉顆粒分布通常屬于連續分布狀態。在級配理論研究中，應根據連續粒度分布的特性建立數學模型。對于給定條件下材料的堆積密度已開發出預測模型，Andreasen[41]對連續粒徑分布粉體的充填行為進行了研究，采用Gaudin-Schuhmann(G-S)方程描述真實粒徑分布，即

(3)

其中，d為顆粒粒徑；F(d)為小于粒徑d的累積質量分數；Dmax為顆粒的最大尺寸；β為特征參數。研究發現，β=0.5～0.8時，堆積體系具有最高的堆積效率。輥式破碎機、顎式破碎機和棒磨機細粒級產物符合式(1)，但球磨機產物僅近似符合[42]。

G-S方程認為，顆粒體系存在粒徑無限小的顆粒分布，不符合現實情況。Funk和Dinger[8]將最小粒徑Dmin引入G-S方程，發展為Alfred方程，即

(4)

通過計算機模擬發現，β=0.37時，系統有最密堆積。但Suzuki等[43-45]認為，對于致密的堆積系統，β的最優值應為0.5～0.8。不同學者對于最優β值的差異，可能是由于試料的細度不同[46]。

在水煤漿領域，最常用和更適用的表征粒度分布的公式為Rosin-Rammler公式[46]，即

(5)

其中，α為影響粒度分布曲線形狀的特征參數；dx為影響粒度分布曲線整體大小的特征尺寸，為F(d)=63.21%時的值。α=0.7～0.8時，顆粒系統有最緊密堆積。

2.2 隔層堆積理論

由于實際粒度分布大多為連續分布，現有理論無法通過直接計算得出連續分布的堆積效率。針對該問題,張榮曾等[46-47]提出了隔層堆積理論，即對連續分布先作離散處理，再按粒徑與孔徑比劃分成若干窄級別，進行隔層隨機模擬堆積，用于計算任意粒度分布的堆積效率。Tu等[42,48]在此基礎上，提出一種相似但計算簡易的評價堆積效果方法，以堆積效率E作為指導制漿試驗的指標。

新的隔層堆積理論的具體推導和假設：

首先，根據顆粒從小到大，將顆粒劃分為n個窄級。S為相鄰粒度分級的粒度比，Vi為第i級顆粒的體積分數(%)，ε為第i級顆粒空隙度，di為第i級顆粒的最大尺寸。每層粒度非常窄時，可用來代表本層的整體粒度。由此可得到

(6)

(7)

為了保證細顆粒完全填充粗顆粒的空隙，粒度比應不小于5[49],需將細粒度級的顆粒填充成更粗的粒度，而不是與其相鄰的粗粒度級，因此為了保證粒度比S*>5，需跳過一定數量的級數,記為m。跳過m級粒度后，(i+m)級與i級的粒度比S*=Sm。對于球體，若S*>5，可認為第i級顆粒可完全填充到(i+m)級的孔隙。為便于計算，記n為m的整數倍，每m個級數算作一層，進行隔層堆積，計算過程為：

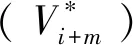
(8)

其中，Vti為第i級所有顆粒的體積分數。由于第i級不僅包含本級顆粒，也包含下一個隔層填充顆粒的整體，因此有Vti>Vi。若第(i+m)級的空隙(εi+m)完全容納第i級中包含的所有顆粒Vti，則

(9)

(10)

(11)

同理，第(i+2m)級的顆粒應包含本級顆粒以及第(i+m)級的所有顆粒，此時第(i+2m)級的體積分數也可由式(11)推導出。第1～m級填充到第(m+1)～2m級,，第(m+1)～2m級填充到第(2m+1)～3m級，以此類推最終第1～(n-m)級的顆粒均可填充到最后的第(n-m+1)～n級。所有顆粒所占空間體積(包含其所占的空隙)為

(12)

得出該顆粒體系的堆積效率E為

(13)

新的模型進行了如下假設和簡化：① 粒子是無孔的，且空間均勻分布；② 整個系統可分為有限的微團簇(micro-cluster)，每個堆積模式和粒度分布相同。 ③ 微團簇可變形、重組和重新堆積，而不改變堆積密度。不同于干粉狀態，除了顆粒無孔假設，以上假設和簡化在懸浮液狀態下，較接近實際。

2.3 分形級配理論

除了隔層堆積理論，分形理論在粒度級配方面也有很多發展和實踐，以指導粒度級配和提高制漿濃度。在應用分形理論前，首先要證明煤的粒度分布是否具有分形特征，然后分析分形特征與堆積密度的關系[11,14,31,38,50-52]，Yang等[14]從分形定義推導出當顆粒符合分形理論時的分布公式。

分形理論研究不規則幾何，用自相似性描述圖形、現象和原理，反映了復雜形體占有空間的有效性[53]。近年來，分形理論在多孔介質滲透率模擬、動態紋理分類、絮凝結構分析等方面得到應用，并取得良好效果[53-58]。分形對象遵循的相似律為

M(L)～LDf，

(14)

式中，M(L)為分形物體的測量值，如直線的長度、表面的面積、物體的體積；L為長度比例尺；Df為分形維數[59],計算公式為

(15)

其中，γ為線性相似比；N為在γ值下的測量值[53]。可轉化為

(16)

式中，x和xmax分別為分形材料的長度尺度和最大長度尺度;N(x)和N(xmax)分別為在長度尺度x和xmax下材料的測量值。

經研磨后的煤顆粒分布，可采用式(3)～(5)連續性方程描述，將分形理論應用于連續方程。對式(16)兩邊微分，則從粒度x～(x+dx)內的煤粒數為

(17)

x～(x+dx)內的煤顆粒質量dM為

(18)

其中，ρ為煤樣真實密度；kV為量綱分析得出的體積系數。根據煤粉粒徑小于x的累積函數定義，可得

(19)

其中，xmin為分形材料最小長度尺度;Mt為顆粒總質量;M為小于粒徑x的顆粒總質量。式(19)與式(4)相似。由于水煤漿顆粒是三維系統，基于分形理論，其分形維數Df=2～3。

3 粒度級配的應用和工業實踐

3.1 隔層堆積級配的應用

近年來，隔層堆積理論在最佳堆積的驗證和指導煤粒度級配提升方面均取得了較好的效果[14-42,46-48,60]。

對于Rosin-Rammler粒度分布(式(5))，采用解析法求最佳α值較困難。張榮曾等[47]采取離散化方式求解，采用在計算機上先按等比級數將粒度分布劃分為多個窄粒級，然后隔層進行隨機充填，并計算堆積效率，得出堆積效率最高的模型參數α=0.7～0.8，這與實際制漿經驗過程中的最佳α值接近。同理，計算Alfred分布(式(4))在不同粒度下限時的堆積效率與分布參數β的關系，并與Rosin-Rammler粒度分布進行比較，結果如圖2所示。

圖2 不同粒度分布參數與堆積效率關系[47]

從圖2可知，Rosin-Rammler粒度分布的堆積效率比Alfred粒度分布略低，但相差不大；Rosin-Rammler粒度分布參數與堆積效率的關系曲線比Alfred粒度分布平緩，說明參數對堆積效率的影響不敏感，在生產中有較強的適應性。

煤粒度采用式(3)～(5)連續性方程表達時，隔層堆積理論不僅可計算粒度分布函數的理論堆積效率，也可計算實際煤顆粒的堆積效率，以預測同種煤、不同顆粒分布情況下制漿濃度的相對大小。Tu等[42,48]通過隔層堆積理論公式計算煙煤和褐煤不同粒度級配的堆積粒度，并通過制漿試驗驗證(圖3)。從圖3可以看出，褐煤和煙煤水煤漿最大成漿濃度(100 s-1剪切速率下黏度為1 Pa·s時的濃度)與堆積效率呈較強的線性關系。相同堆積效率下，不同煤種的制漿濃度差異主要可能是由內在水分差異造成。

圖3 堆積效率與最大成漿濃度的關系[48]

3.2 分形級配理論的實踐和應用

近年來，學者將分形理論引入到粒度級配，以指導提高顆粒堆積效率和提高制漿濃度，并進行了很多理論驗證和實踐應用[11,14,31,38,50-52]。

王俊哲等[32]研究了分形理論與煤粉粒度級配的相關性，運用分形理論分析了不同粒度煤粉的粒徑分布特性(圖4)，擬合曲線有較好的線性關系，線性相關系數在0.95以上，呈現分形特征，說明較粗和較細煤粉均具備分形特征，且分形維數低于2.3。通過將煤粉等比例級配，其結果分形維數在2.5以上，高于未級配煤粉分形維數，可通過測定煤粉的分形維數評判級配好壞。在推導分形關系時，假設最小粒度為0，這與實際不符，產生了誤差，且擬合時線性相關系數有待進一步提高。

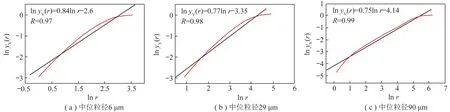
圖4 不同粒度的煤顆粒累積含量(yV)與粒徑(r)的雙對數關系擬合[38]

通過與實際粒度擬合和對比，發現式(19)擬合實際粒度分布時，仍有一定誤差。Yang等[14]以分形理論為基礎，對褐煤水煤漿填料狀態的分形模型進行系統研究，分析了分形模型在不同顆粒體系中的堆積效率和回歸水平，發現褐煤顆粒體系的堆積效率主要由74 μm以下的顆粒分形特性決定。通過從最小粒度到74 μm進行擬合，發現分形維數的擬合系數均在0.99以上，有較好的一致性。同時通過隔層堆積理論計算了不同分形維數下的堆積效率，發現分形維數在2.6～2.7時堆積效率最高，并驗證了對于同煤種此時的水煤漿制漿濃度最大，可提高約2.9%的成漿濃度。其推導出的分形維數公式和Alfred模型相似，與張榮曾等[47]預測的最大堆積效率系數接近。

3.3 三峰級配

在工業實踐中，需通過合理的磨煤機型選擇較好的流程優化以實現粒度級配。三峰級配制水煤漿技術在工業上應用較多，對于水煤漿濃度的提高較顯著[29-33]。

典型的三峰級配工藝流程包括：2個粗漿配置系統、4個細磨系統和2個超細磨系統，通過控制粗漿在細磨和超細磨系統的分配以及回流比例，來控制粗漿、細漿和超細漿的質量比例[30]。在級配粒度控制方面，為了實現相鄰粒級顆粒有效的堆積填充，三峰級配最終確定棒磨粗漿粒徑在 100～150 μm，細漿粒徑在20～30 μm，超細漿粒徑在4～8 μm。細漿和超細漿的粒度取決于粗漿粒度，且每級平均粒度直徑比接近5，粗漿、細漿和超細漿的質量比為85%∶10%∶5%。在工業應用中，三峰級配要添加磨煤設備，重整制漿流程，增加了初期投入，同時在運行過程中，增加的磨煤動力和磨球損耗增加了運行成本，但投入遠小于提高水煤漿濃度帶來的收益。在陽煤豐喜泉稷公司應用過程中，水煤漿濃度由60.1%提高到64.2%，另一家企業在表觀黏度滿足生產要求的條件下，煤漿濃度提高3.6%[30,33]。

4 結語和展望

本文分析了粒度級配對水煤漿的影響，指出在水煤漿制漿過程中，粒度級配只涉及物理破碎和研磨，能耗相對較小，可顯著提升濃度，具有廣泛的適用性和經濟性。論述了近年來新發展的粒度級配理論和模型，給出了具體的計算方法和公式，以及假設和適用性。通過舉例論述近年來粒度級配理論的應用和在工業生產中的實踐和效果。

在粒度級配提高水煤漿濃度的基礎理論和應用實踐方面，國內外學者已做了大量工作。但在具體的理論細節和應用方面有待進一步研究：

1)隔層堆積對于任意粒度分布的簡化計算方面，可給出更加便捷和貼近實際的計算方法，前期假設有待具體化。

2)目前分形級配理論對特定粒度分布擬合較好，但對于三峰分布和不規則粒度分布擬合較差，可進一步挖掘理論方法。

3)三峰級配的粒度堆積評價和指導理論有待進一步研究。

基礎理論對于工業實踐的系統性影響有待積累和總結，特別是磨煤設備選型和流程優化實現最優級配方面，以及整體經濟性評價方面。建議在粒度級配模型基礎上，引入煤內在水分、顆粒間作用力等影響因素，建立跨煤種的濃度預測模型。