擬泡-乳曳力模型在大型高溫費托流化床反應器中的CFD模擬研究

王 騰，夏梓洪，陳彩霞

(華東理工大學 資源與環境工程學院，上海 200237)

0 引 言

費托合成技術是煤間接液化的核心部分，是煤清潔利用的關鍵技術之一[1]。根據目標產物的不同及采用的催化劑、反應器形式和反應條件不同，費托合成又可分為低溫費托合成和高溫費托合成2種工藝[2]。其中高溫費托合成工藝在獲得大量油品的同時，還可以獲得較多的烯烴、含氧化合物等更高附加值的化學品，是未來煤制油行業的重要發展方向之一[3]。氣固鼓泡流化床由于其氣體和固體顆粒之間傳熱性能好，床內溫度均勻，在高溫費托合成反應中具有顯著的應用優勢[4-5]。

目前，對氣固鼓泡流化床中流動、傳遞和混合過程的研究主要依靠試驗完成，諸多關鍵參數難以直接測量，流場內部特性仍缺乏很好的理解。計算流體力學(CFD)可以得到氣固流場的詳細信息及其隨時間變化的動態行為，已成為流化床反應器開發、設計和放大應用的重要輔助工具。基于雙流體模型(TFM)的CFD模擬已經成功預測了氣固流化床內的流體力學特性。然而雙流體模型基于局部平均的假設，認為單位控制體內氣固兩相均勻分布，網格必須足夠小才能正確揭示介尺度(氣泡或顆粒團聚物)的所有細節[6]。對于氣固鼓泡流化床，網格尺寸至少需要2～4倍顆粒直徑[7-8]。如此細密的網格導致工業級流化床裝置的計算量遠超現有計算能力。未經修正的粗網格計算又會導致顯著的計算誤差[9]。因此，應用粗網格模擬大型工業化裝置時需要結合非均勻曳力模型對曳力進行修正[10]，以考慮網格尺度內未被解析的局部非均勻結構(或稱介尺度結構)對氣固流場產生的影響。Wang等[10]采用SGS模型，驗證了使用200倍粒徑粗網格可以得到與試驗結果一致的固含率分布情況。

氣泡作為氣固鼓泡流化床中最典型的非均勻結構特征，對氣固相間曳力具有決定性影響。要建立可靠的非均勻曳力模型，需考慮氣泡尺寸對曳力的影響。然而，現有的非均勻曳力模型均是在雙流體模型的基礎上對傳統氣固曳力進行修正，以氣含率函數的形式體現局部非均勻性對曳力的影響，不能完全反應氣泡尺寸的影響。實際上，在氣固鼓泡流化床中，氣體分別分布于氣泡相和乳化相中，氣體的不同存在形式使氣固相間作用力的作用機制也不同。乳化相內氣體和顆粒間通過直接接觸的方式作用；氣泡與乳化相內顆粒間則通過氣泡相和乳化相作用的方式間接作用，且受氣泡尺寸的影響。為了描述氣泡相與顆粒相之間的曳力，本文提出一種基于歐拉多相流框架的新思路——擬泡-乳三相曳力模型(Pseudo bubble-emulsion triple-phase drag model，PBTD)。PBTD模型將氣固鼓泡流化床分為乳化相氣體、乳化相顆粒以及氣泡三相，分別建立守恒方程，體現氣泡的非均勻特性對氣固曳力的影響，乳化相內的氣固曳力以及氣泡相與乳化相內顆粒的曳力分開考慮。

本文采用開發的非均勻曳力模型對大型工業化高溫費托流化床反應器進行模擬，考察床層膨脹高度、床層截面氣泡和顆粒體積分數的分布規律，研究H2和CO的傳質反應速率以及氣體組分沿床層高度的分布，并將出口氣體組分與試驗結果對比，探討該模型在模擬大型工業化流化床反應器中的適用性。

1 模擬方法

1.1 控制方程

本文采用擬泡-乳三相模型將流化床系統分為氣泡相、顆粒相和氣相三相，顆粒相和氣相組成擬乳化相。氣泡相(b)、顆粒相(s)和氣相(g)分別采用一套控制方程進行封閉。

質量守恒方程：

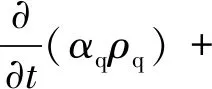
(1)

動量方程：

(2)

(3)

(4)

式中，q為g、b、s相；α為體積分數；ρ為密度；u為速度向量；g為重力加速度；?·τ為黏性力；α?p為靜壓力；?ps為固相壓力；Fg、Fb和Fs為相間作用力項。

應力-應變張量項τq表示為

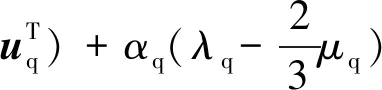
(5)

式中，μq為q相剪切黏度；λq為q相體積黏度；I為單位張量。

顆粒相體積黏度項λS[11]為

(6)

顆粒相剪切黏度μs包括動力部分、碰撞部分和摩擦部分，即

μs=μs,col+μs,kin+μs,fr，

(7)

顆粒相碰撞黏度[12]為

(8)

顆粒相動力黏度[13]為

(9)

顆粒相摩擦黏度[14]為

(10)

顆粒相壓力ps方程[11]為

ps=αsρsΘs+2ρs(1+ess)αs2g0,ssΘs，

(11)

其中，ds為顆粒直徑；ess為顆粒碰撞彈性恢復系數，取0.9；Θs、g0,ss分別為顆粒溫度、徑向分布函數；I2D為偏應力張量中的第二不變式；φ為內摩擦角。

徑向分布函數[15]為

(12)

式中，αs,max為最大顆粒堆積體積分數。

顆粒溫度方程：

(13)

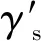
(14)

能量傳遞項φs計算公式為

φs=-3βgsΘs。

(15)

式中，βgs為氣固相間動量交換系數。

1.2 湍流模型

采用混合(Mixture)RNGk-ε模型[16-17]，壁面函數選擇標準壁面函數。湍流動能和湍流耗散率控制方程如下：

(16)

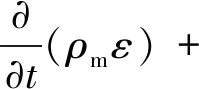
(17)

其中：

(18)

(19)

(20)

(21)

Gk,m=μt,m(?um+(?um)T)∶?um，

(22)

式中，ρm為混合密度；μm為分子黏性，um為混合速度；μt,m為湍流黏度；Gk,m為湍動能產生項；αq、ρq、μq、uq分別為q相的體積分數、密度、黏度和速度；Cμ、C1ε、C2ε為湍流模型參數；σk、σε為湍流動能k和湍流耗散率ε的湍流普朗特數。

1.3 曳力模型

氣固流化床中，氣固兩相密度相差很大，其他作用力對氣固流場的影響有限，可忽略不計，只考慮曳力的作用。由于采用了三相假設，原則上會出現3組相間曳力：氣泡-顆粒曳力、氣泡-乳化相氣體曳力以及乳化相內氣體-顆粒曳力。本文在模型推導過程中，將顆粒相和氣相看作“擬乳化相”，考慮氣泡與擬乳化相之間的曳力，并最終將該曳力體現在顆粒和氣泡的動量方程中。在計算氣泡-擬乳化相曳力時采用擬乳化相的密度和黏度，以考慮乳化相中氣體的存在對氣泡和乳化相之間作用力的影響。因此式(2)～(4)中相間作用力項可表示為

Fg=βg-s(ug-us)，

(23)

Fb=βb-s(ub-us)，

(24)

Fs=βb-s(ub-us)+βg-s(ug-us)，

(25)

式中，βg-s、βb-s分別為乳化相內氣體-顆粒動量交換系數、氣泡-顆粒動量交換系數。

在考慮氣泡與乳化相顆粒相間曳力時，乳化相為連續相，氣泡為離散相。根據牛頓第二定律，乳化相對氣泡相的曳力等于氣泡相對乳化相的曳力，因此根據通用曳力公式，在單位控制體積內，單個氣泡對擬乳化相曳力的表達式為

(26)

其中，CDb為氣泡群曳力系數；ρe為擬乳化相密度；Uslip,i為相間表觀滑移速度，Uslip,i=(ub-ue)(1-αb)。由此可得，單位控制體內，所有氣泡與擬乳化相之間的曳力為

(27)

根據A類雙流體模型曳力系數公式[13]，氣泡-擬乳化相之間的相間動量交換系數可表示為

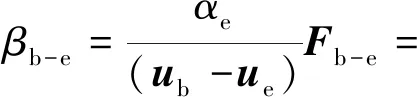
(28)

式中，αe為乳化相體積分數；ue為乳化相速度。

由于在PBTD模型中，氣泡-擬乳化相曳力最終反映在顆粒相的動量方程中。因此將式(28)中的ub替換為us。氣泡相與顆粒相之間的等效相間動量交換系數為

(29)

采用Ishii和Zuber[18]提出的公式，即

CDb=CDb0(1-αb)-0.5，

(30)

式中，CDb0為單氣泡曳力系數，由Darton和Harrison[19]關系式計算所得。

(31)

(32)

其中，Reb為氣泡雷諾數；db為氣泡直徑；μe為擬乳化黏度。

db采用Mori和Wen[20]提出的經驗公式，即

(33)

db0=0.003 76(u0-umf)2,

(34)

式中，dbm為最大氣泡直徑；db0為初始氣泡直徑；h為床層高度；Dt為床層直徑；u0為入口氣速；umf為最小流態化氣速。

本文模擬所用反應器內置大量冷卻盤管，內構件的存在會對氣固流體動力學特征產生影響，其復雜程度也高于空塔流化床反應器。Ozawa等[21]發現在帶有豎直列管的氣固流化床中，A類顆粒和B類顆粒床層內部氣泡仍符合隨著床層的升高氣泡尺寸逐漸增大，但受內構件的影響，平均氣泡尺寸均小于Mori-Wen關系式預測值。Ozawa等根據列管的影響，對Mori-Wen氣泡尺寸公式中的最大氣泡尺寸進行修正，提出以下最大氣泡尺寸修正公式：

dbm=0.59[DtHt(u0-umf)]0.4，

(35)

式中，Ht為列管中軸線距離。

擬乳化相密度ρe和黏度μe受氣體和固體顆粒濃度的共同影響，密度通過擬乳化相內部氣固兩相體積加權平均求得，黏度計算采用Ishii和Zuber[16]的經驗公式，具體為

ρe=ρs(1-αeg)+ρgαeg，

(36)

μe=μg(1-αes/αs,max)-2.5αs,max，

(37)

其中，as,max為乳化相中最大顆粒堆積密度，取0.63；αeg和αes分別為乳化相中相對氣含率和固含率，計算公式為

(38)

αes=1-αeg。

(39)

擬乳化相內的氣固相間作用力采用傳統Gidaspow曳力模型[12]，需要注意的是，方程中的氣固體積分數采用擬乳化相內的相對體積分數，相間動量交換系數βg-s表達為

(40)

(41)

CD=0.44(Res>1 000)，

(42)

(43)

1.4 傳質模型

基于擬泡-乳三相曳力模型的假設，相間傳質存在于氣泡相與擬乳化氣相之間，該相間質量傳遞主要由氣流穿流項和擴散項兩部分組成。Sit和Grace[22]認為在細小顆粒的流化床中，擴散速率是相間質量傳遞速率的控制因素，而在粗顆粒流化床中，氣流穿流是相間傳遞速率的決定性因素。Kunii和Levenspiel[23]將氣泡與乳化相之間的質量傳遞過程分為2個步驟：首先氣體通過氣泡傳遞到氣泡暈；其次再從氣泡暈傳遞到乳化相中。并分別用2個交換系數Kbc和Kce的綜合表示氣泡與乳化相之間的交換總系數Kbe。本文采用Kunii和Levenspiel提出的質量傳遞模型描述氣泡與擬乳化相之間的質量傳遞并忽略氣泡暈相，認為氣泡與氣泡暈之間的質量交換系數Kbe等于氣泡與擬乳化相之間的質量傳遞系數，表達式為

(44)

其中，Dg為氣體擴散系數。等號右側第1項為氣體穿過氣泡而引起的質量交換，即穿流貢獻項(through-flow contribution)，第2項為擴散引起的質量交換，即擴散貢獻項(diffusion contribution)。

除了氣泡和乳化相之間的傳質，乳化相內中氣體混合物之間也存在擴散現象。對于多組分氣體中的擴散，組分i在混合物中的質量擴散系數Di,m可表示為

(45)

其中，Xi為組分i的摩爾分數；Di,j為雙組分體系的分子擴散系數，其計算公式為

(46)

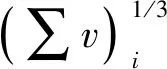
1.5 反應動力學模型

F-T合成反應是一個多種反應并存的復雜反應體系，具有眾多的主反應和副反應，其發生的概率隨催化劑種類和操作條件的不同而變化[24]。主反應主要生成烷烴類和烯烴類產物，副反應包括水煤氣轉化(Water gas shift，WGS)反應以及生成含氧化合物的反應。

主反應為：

(47)

副反應為：

(48)

(49)

關于F-T合成反應的動力學，學者進行了深入廣泛的研究。目前最常用的是考慮合成氣消耗速率的氣體消耗動力學模型[25-29]。本文采用某公司通過試驗測量數據擬合的動力學模型，具體為

(50)

(51)

其中，RFT、RWGS分別為費托反應和水煤氣變換反應速率系數，kmol/(m3·s)；kft、Eft、k1、kwgs、Ewgs為常數，取值分別為：kft=0.003 224 6，Eft=46 239，k1=0.029，kwgs=1.54，Ewgs=7 392。Keq=0.012exp(4 630/T)；P(H2)、P(CO)、P(H2O)分別為H2、CO和H2O的氣相分壓；R為通用氣體常數，取8.314 5 J/(K·mol)。

F-T合成反應除生成烴類產物外還生成相當數量的含氧有機物，兩者相對選擇性是一定值，其中含氧有機物選擇性XCHO為

(52)

其中，m為試驗測得的摩爾流率；prod為出口氣體；feed為入口氣體。由于高溫費托合成的含氧有機物組分復雜，模型采用含量最高的乙醇代表含氧有機物。

1.6 反應器幾何模型及計算條件

計算幾何模型基于某公司開發的4 500 t/a中試規模高溫費托流化床反應器裝置，如圖1所示(L為冷卻盤管長度，D為反應器直徑，D′為冷卻盤管直徑)。反應器高度為24 000 mm，直徑為900 mm。內部冷卻盤管外徑為90 mm，高度為7 000 mm。

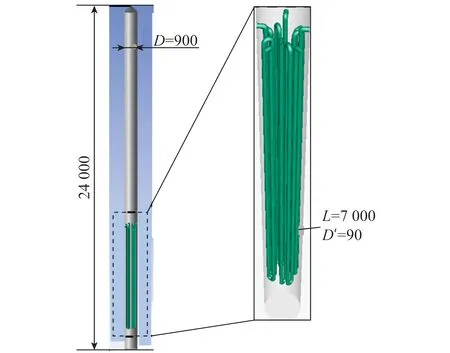
圖1 高溫費托流化床反應器結構示意

采用六面體結構化網格對幾何模型進行網格劃分，網格數量約為88萬，屬于平均尺寸約為600倍顆粒直徑的粗網格。為了捕捉壁面對流場的影響，網格在管壁附近進行了局部加密處理，如圖2所示。

圖2 中試規模高溫費托流化床網格

模擬時氣相和氣泡相采用均勻進氣，進氣速度U0=0.495 m/s。由于催化劑所用顆粒為Geldart A類顆粒，因此氣相進口表觀速度為最小鼓泡速度Umb，為0.007 2 m/s，氣泡相進口表觀速度為(U0-Umb)。入口邊界湍流強度為5%，水力直徑采用幾何直徑。氣相采用無滑移(no-slip)的邊界條件，氣泡相壁面采用自由滑移，顆粒相壁面采用部分滑移(partial slip)，其中鏡面系數(specularity coefficient)設置為0.05[30]，顆粒碰撞恢復系數設置為0.9[31]。相間作用力模型和氣泡尺寸模型通過用戶自定義函數(User defined function，UDF)并耦合到Fluent模擬計算。所用時間步長設置為0.001 s，每個時間步長迭代20步。模擬時間總長為100 s，對50～100 s模擬瞬時結果進行數據采集并進行時均處理。

模擬采用的物性參數見表1。試驗測得床層內部溫度基本均勻，因此本文假設床內溫度均勻，不存在溫度梯度，模擬不涉及床層與冷卻盤管傳熱，只考慮冷卻盤管對氣固流場的影響。

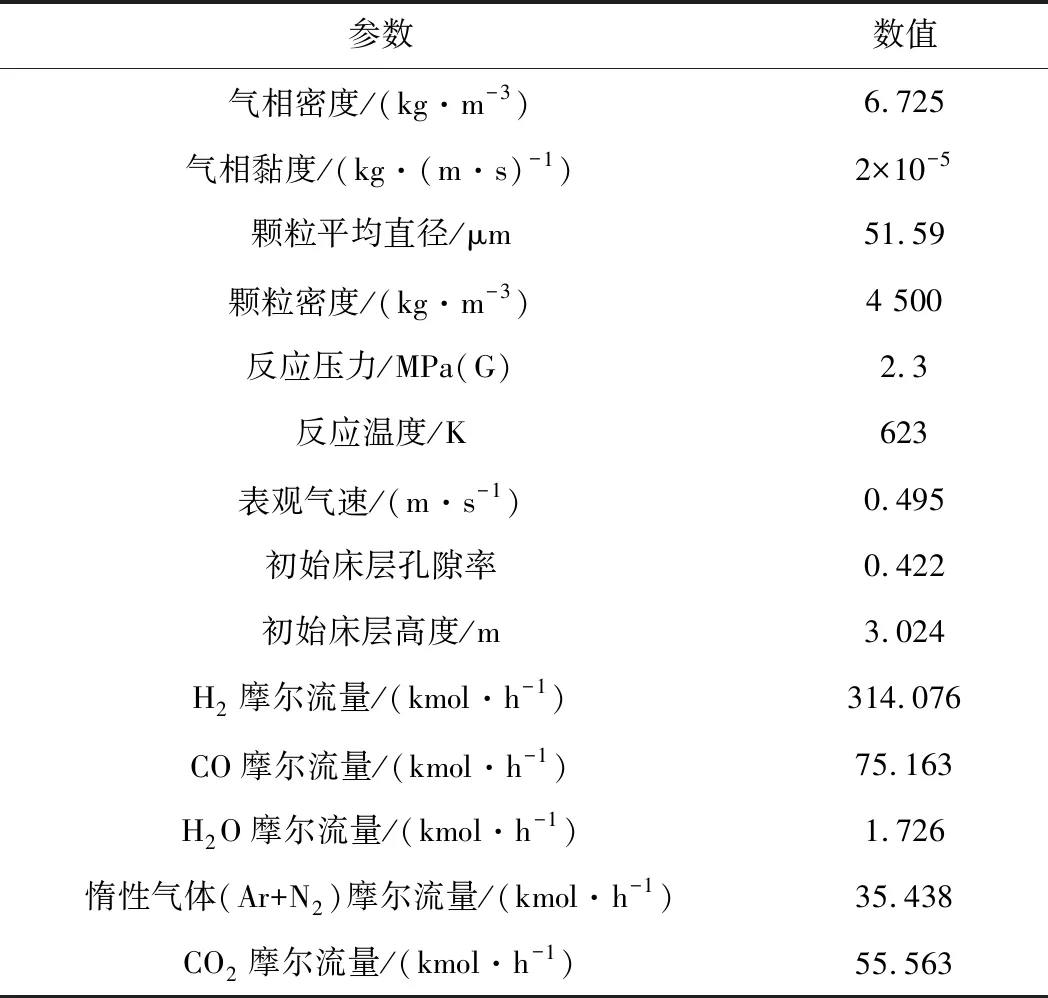
表1 模擬參數

2 結果分析與討論

2.1 總體流化狀態

圖3為采用非均勻曳力模型時模擬的床層膨脹高度情況，可以看出，床層穩定時床層高度為初始床層高度的2倍左右。根據Cloete[32]提出的床層膨脹高度判據：床層膨脹高度應該在固含率0.05的位置，模擬所得床層最終膨脹高度為8.2 m。由于中試裝置處于高溫高壓的惡劣環境，無法進行試驗測量，本文采用Cai等[33]提出的經驗公式(53)計算床層膨脹高度，該經驗公式適用于計算高溫高壓條件下氣固流化床的床層膨脹高度。經計算，床層膨脹高度約為8.1 m，模擬床層膨脹高度和經驗公式預測值的相對誤差為1.2%，PBTD曳力模型能夠在粗網格條件下較好地預測床層的膨脹情況。

(53)

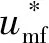
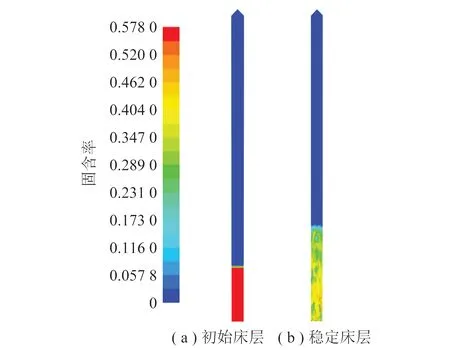
圖3 流化床床層固含率分布

2.2 床層時均相含率分布

床層不同高度處的時均氣泡體積分數和固體顆粒體積分數分布云圖如圖4、5所示。可知冷卻盤管管壁附近，氣泡的體積分數明顯高于其他部分，固含率則相反，管壁附近固含率低于其他部分，說明氣泡趨于沿著冷卻盤管管壁上升，這與Rudisuli等[34-35]的試驗現象一致。在流化床壁面，氣泡體積分數降低，顆粒體積分數升高，這主要是由于顆粒到達流化床床層表面后，氣泡離開床層，顆粒沿壁面下降。表明有內構件存在的流化床仍然具有固體顆粒濃度邊壁濃、中心稀的非均勻分布特點。隨著高度的增加，床層截面氣泡平均體積分數逐漸增大，顆粒平均體積分數逐漸下降，符合流化床顆粒濃度下濃上稀的總體非均勻特性。

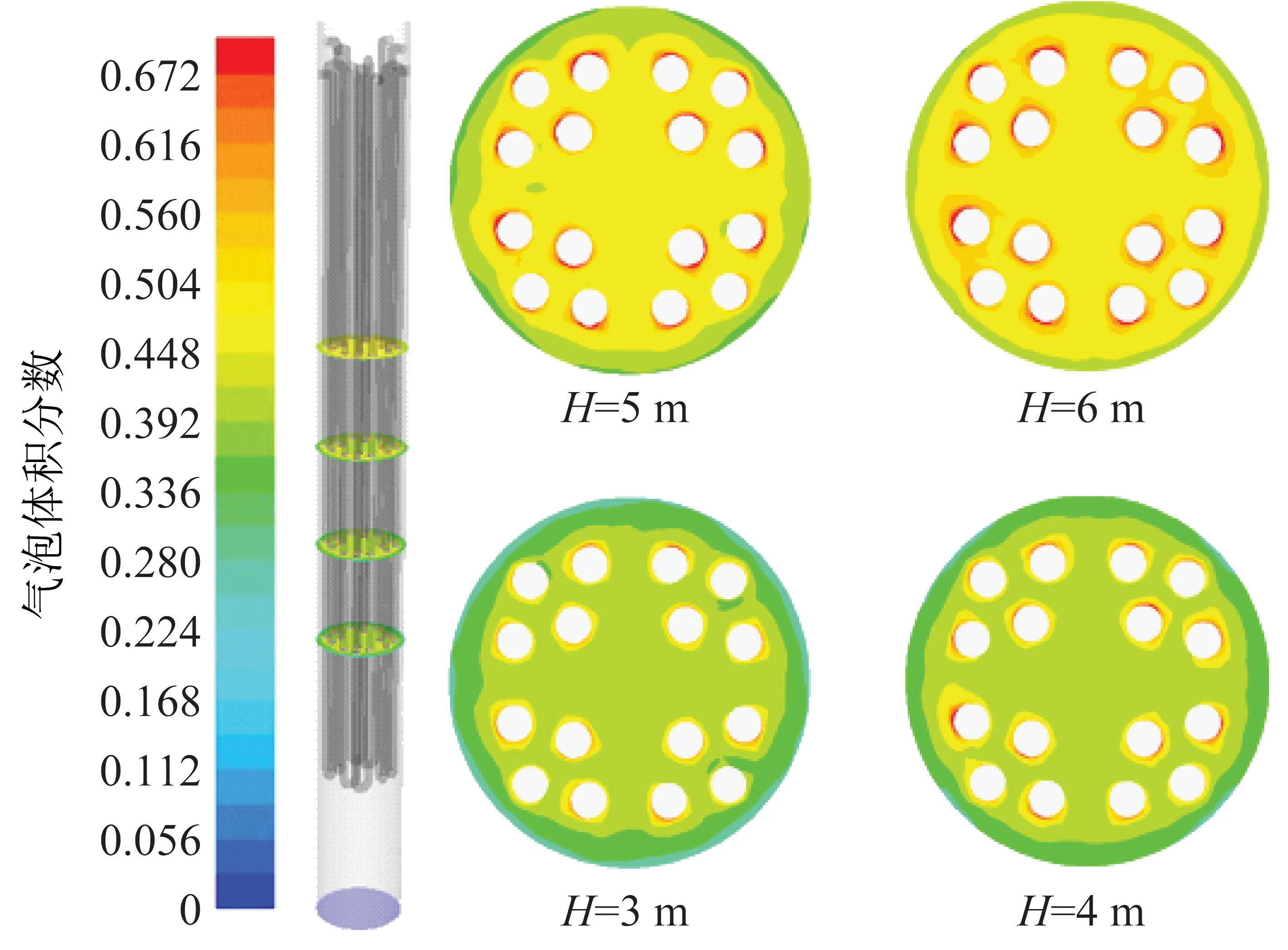
圖4 不同床層高度處時均氣泡體積分數分布云圖

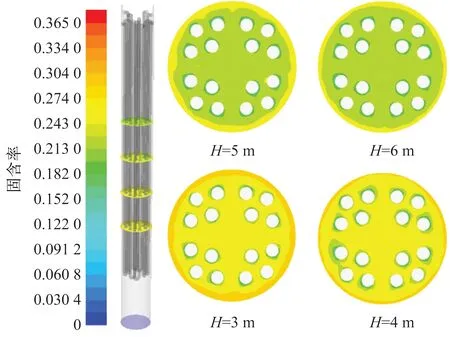
圖5 不同床層高度處時均固含率分布云圖

2.3 傳質速率及各組分濃度分布

合成氣的傳質速率分布云圖和費托反應速率分布云圖如圖6、7所示。可知，CO傳質速率≈H2傳質速率/2，與反應方程中的化學計量比一致。由圖中還可以看到，伴隨著反應器高度的增加，反應不斷進行，CO和H2的傳質速率和F-T反應的反應速率都呈逐漸減弱的趨勢。

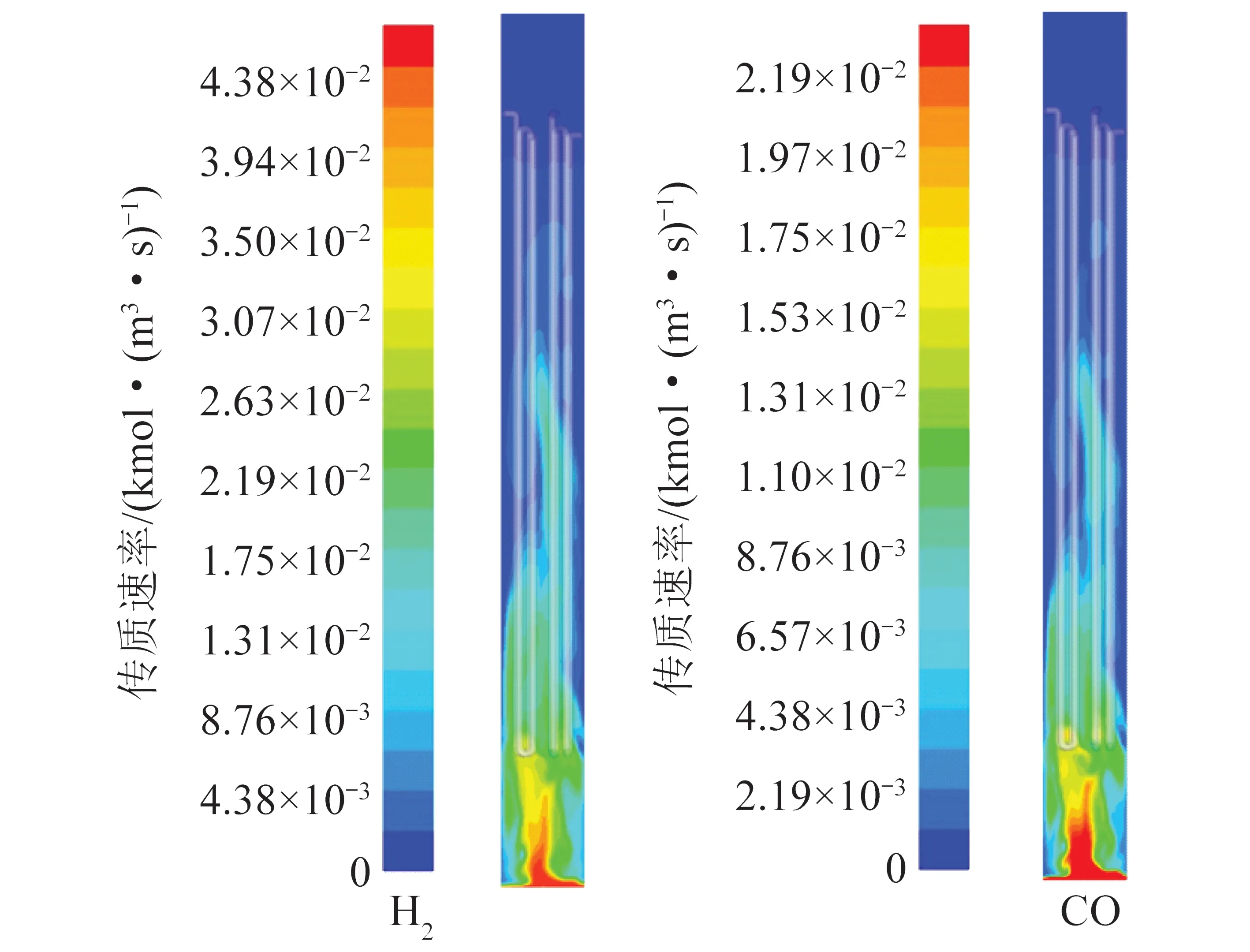
圖6 H2和CO的傳質速率分布

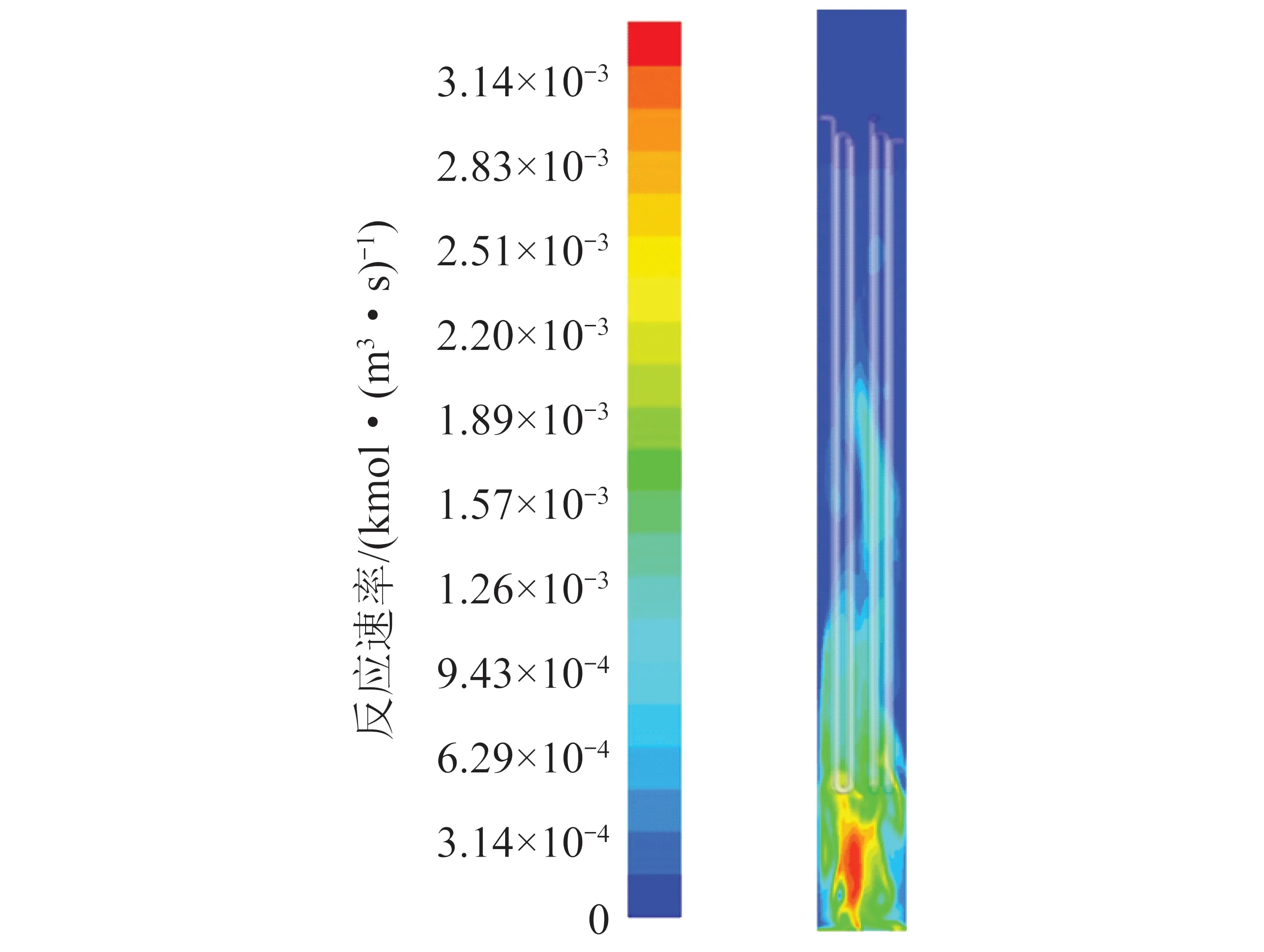
圖7 費托合成反應速率分布

床層內部氣體成分(CO、H2、[—CH2—]、C2H5OH、H2O、CO2)時均質量分數隨流化床床層高度的變化如圖8所示。可知隨著F-T反應的進行，CO和H2被大量消耗，其含量隨床層高度的升高迅速降低。反應生成產物[—CH2—]、C2H5OH、CO2、H2O隨著床層高度的升高逐漸增加。床層1.6 m附近，組分曲線明顯出現一次明顯波折，隨后氣體組分反應速率變緩慢。這是由于1.6 m后床層開始出現冷卻盤管，使氣固流場發生明顯改變，氣泡沿管壁上升，氣體傳質速率降低，因此反應速率隨之降低。

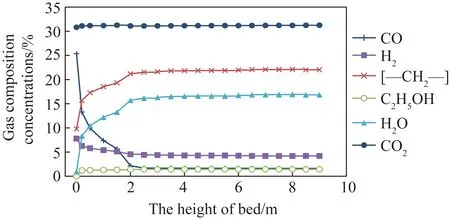
圖8 氣體組分濃度沿床層高度的分布

反應器出口氣體組分質量分數與試驗測量數據對比如圖9所示，可知主要產物氣體組分質量分數的模擬值與試驗值之間比較接近，主要生成產物(H2O、CO2、C2H5OH和[—CH2—])質量分數相對誤差在1.5%～16.0%，表明PBTD模型基本適用于工業規模的反應器模擬。

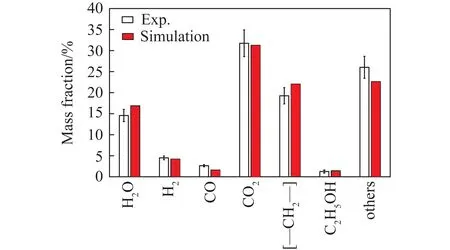
圖9 反應器出口氣體組分濃度

3 結 論

1)采用PBTD模型結合Ozawa等提出的氣泡尺寸模型，在粗網格條件下對反應器進行模擬，得到的床層膨脹高度與文獻公式預測值的相對誤差為1.2%。PBTD模型能夠呈現氣泡趨于沿著內構件管壁上升的運動規律，發現有內構件的氣固流化床仍然具有顆粒濃度下濃上稀、邊壁濃中心稀的宏觀非均勻特性。

2)CO傳質速率約為H2傳質速率的1/2，與反應方程中的化學計量數一致。模擬結果顯示，隨著反應進行，CO和H2傳質和反應速率逐漸降低。

3)冷卻盤管的存在影響氣固混合效率，從而影響反應速率。模擬出口主要產物氣體組分(H2O、CO2、C2H5OH和[—CH2—])質量分數與試驗測量值相對誤差在1.5%～16.0%，表明本文開發的基于非均勻假設的PBTD模型適用于模擬工業規模的反應器，為大型工業化流化床反應器提供了實用的模擬方案。