基于深度置信神經網絡的變風量空調送風量的預測

雷 蕾，王 寧，鄭 皓，薛 雨

（1.桂林電子科技大學，廣西桂林 541004；2.大連理工大學，遼寧大連 116024）

0 引言

隨著空調能耗在建筑能耗占比的不斷增大，變風量空調（VAV，Variable Air Volume Air-Conditioning）以顯著的節能優勢成為國內外空調領域的熱門研究對象。變風量空調涉及溫度、濕度、壓力和流量等多個參數，由于這些參數之間的非線性性和相互耦合特性，導致變風量空調送風量的預測出現不精確、不穩定現象，影響變風量空調的節能和室內舒適性［1-3］。因此，精確預測變風量空調的送風量是一項丞待解決的問題。

近年來，針對變風量空調的節能研究主要集中在負荷預測方面，文獻［4］建立MSA-SVR（Support Vector Regression Machine Optimized by Modified Simulated Annealing）空調負荷預測模型，有效地提高了空調負荷預測的精準度和穩定性。 文 獻［5］采 用 IDEA（Improved Differential Evolution Algorithm）優化小波神經網絡的方法建立空調冷負荷預測模型，提高了空調冷負荷預測的速度和精度。文獻［6］提出一種基于集成方法的深度置信神經網絡模型對空調系統冷負荷進行預測，提高了空調系統冷負荷預測的穩定性和魯棒性。上述研究均是對空調系統的負荷進行預測，關于變風量空調送風量的預測研究則相對較少。目前送風量的預測主要依靠空調負荷的預測值，當空調負荷預測出現較大誤差時，由于誤差的傳遞性導致送風量的預測誤差增大。鑒于上述問題，文獻［7］利用CFD模擬軟件對整車空調的送風量進行預測，該方法可以預測出整車空調的送風量。CFD技術固然可行，但是計算結果完全依賴于初始邊界條件和參數設置，模擬時間長且適應性較差。除了軟件模擬技術，一些學者利用神經網絡方法對VAV的送風量進行預測，文獻［8］將模糊控制與BP神經網絡相結合，建立基于模糊神經網絡變風量空調送風量的預測模型，并驗證了該模型的有效性和可行性。文獻［9］建立基于RBF神經網絡空調風管恒風量的預測模型，較為準確地實現了風量預測。由于上述對空調送風量的預測模型均為淺層神經網絡，在預測復雜問題時，容易出現收斂速度較慢和陷入局部最小等問題［10］。為彌補淺層神經網絡在計算復雜問題時存在的不足，Hinton在2006年提出深度置信神經網絡方法，該算法含有多層隱含層，可以映射復雜的非線性關系，同時具有較強的自學習能力，能夠克服預測模型的非線性、強耦合性以及時變等不確定影響因素，在處理含有復雜數據預測時具有較好的穩定性，屬于深度學習方法的一種。目前深度置信神經網絡已被應用到建筑冷負荷預測、燃煤鍋爐氮氧化物排放預測和短時交通流量預測等研究中，并實現了對復雜數據的精準預測［11-13］。

為實現VAV送風量的精準預測，本文以VAV末端裝置為研究對象，建立基于深度置信神經網絡的變風量空調送風量的預測模型。

1 變風量空調送風量的預測模型

VAV系統是一種全空氣空調系統，它通過向房間輸送足夠量經過處理的空氣來平衡房間內的熱量和濕度負荷，達到人們所需的溫濕度要求。圖1示出典型單風道VAV系統結構，根據區域負荷的變化，通過調節VAV末端風機轉速和風閥開度控制送風量，并向空調控制器反饋工作狀態和控制偏差［14］。

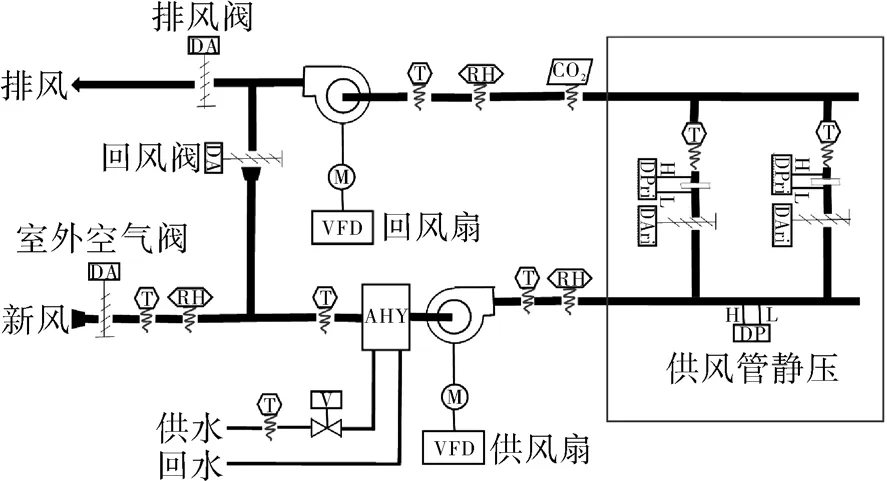
圖1 典型單風道VAV系統結構Fig.1 Typical single duct VAV system structure

1.1 深度置信神經網絡模型理論

深度置信神經網絡（DBN，Deep Belief Neural Network）是深度學習的一種重要算法，由輸入層、中間層（隱層）和輸出層構成。它是一種利用無監督逐層訓練的方法快速地從底向上逐層訓練整個神經網絡，使得網絡具有較快的訓練速度。

基于DBN算法的VAV送風量預測模型的結構如圖2所示，共有4層結構。第1層是顯層，即為輸入層，由室外氣象參數和VAV歷史送風量組成；第2層和第3層為隱層，雙隱層結構能夠在保證預測精度的前提下避免局部收斂。第4層是輸出層，即模型中預測日t時刻的VAV送風量。

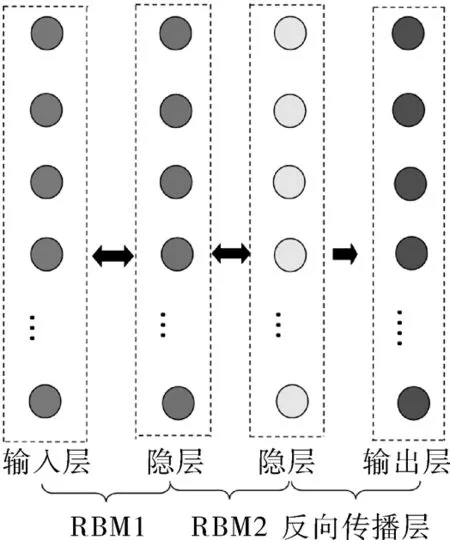
圖2 DBN結構Fig.2 DBN structure

DBN由一定數量的受限玻爾茲曼機（RBM，Restricted BoItzmann Machine）堆疊而成。DBN在訓練RBM的過程中，通常根據RBM的能量函數求解其顯層和隱層的激活概率，然后得到RBM訓練參數的更新規則。RBM是一種基于能量函數的特殊神經網絡結構，對任意一個RBM的結構而言，其能量函數都可定義為：

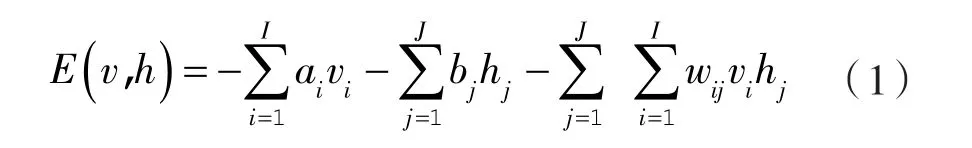
式中 I，J——顯層和隱層單元數；

vi，hj——第 i個顯層神經元和第 j個隱層神經元；

ai，bj——第 i個顯層神經元和第 j個隱層神經元的偏置；

wij——連接vi和hj之間的權重。

根據隱層和顯層神經元的激活概率，重新計算顯層和隱層神經元之間的連接權重和偏置，可得 RBM 參數 θ={wij，ai，bj}的更新規則：

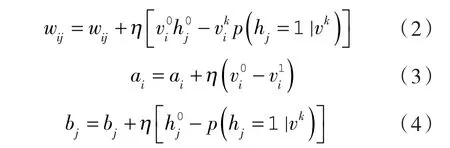
式中 η ——學習率，在四層的DBN結構中一般取值為0.01。

在整個DBN訓練過程中，首個RBM的顯層產生一個向量，然后通過RBM網絡傳遞到隱層，反過來可以重構顯層，根據重構層和顯層的差異更新隱層和顯層之間的權重和偏置，直到訓練誤差達到設定要求時停止更新。DBN訓練過程如圖3所示，主要步驟分為兩步［15］：

圖3 DBN訓練過程Fig.3 DBN training process

（1）在RBM中，通過逐層訓練得到參數。輸出端與BP神經網絡連接得到輸出數據，完成整個DBN訓練的前向階段。

（2）根據實際數據與輸出數據的誤差，自頂向下反向傳播至每一層的RBM，逐層對每一層的RBM進行調優，使得參數 達到全局最優，完成整個DBN的訓練。

通過優化上述的網絡結構參數來保證結果具有較高的精準度，本預測模型選取兩層隱含層，并使用經驗公式：

式中 n ——輸入層神經元個數；

M ——隱含層神經元個數；

k ——樣本數。

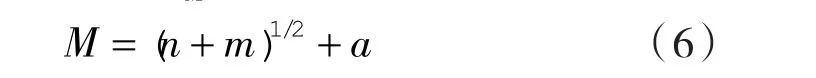
式中 m——輸出層神經元個數；

a——［0，10］之間的常數。

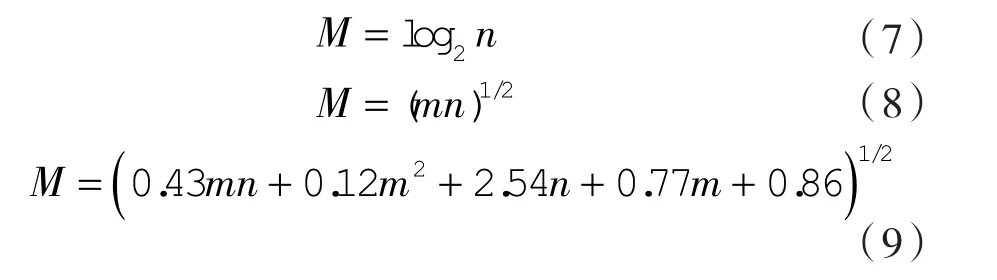
根據以上公式和在仿真過程中對隱含層神經元的個數和學習率不斷調試，最終選取第一層隱含層神經元為14個，第二層隱含層神經元為7。

1.2 預測模型的建立

VAV送風量預測模型中各影響因素與送風量之間的數學關系如下：

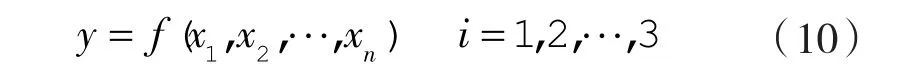
其中，y為VAV的t時刻送風量，xi為第i個影響送風量的參數，包括前一天t時刻的送風量、前兩天t時刻的送風量、前一天t時刻的室外溫度、前兩天t時刻的室外溫度、當天t時刻的室外溫度、當天t-1時刻的室外溫度、當天t-2時刻的室外溫度、當天太陽輻射溫度和當天大氣濕度，n為影響送風量的因素個數，f為DBN的不確定函數關系。

圖4示出基于DBN的VAV送風量的預測流程。

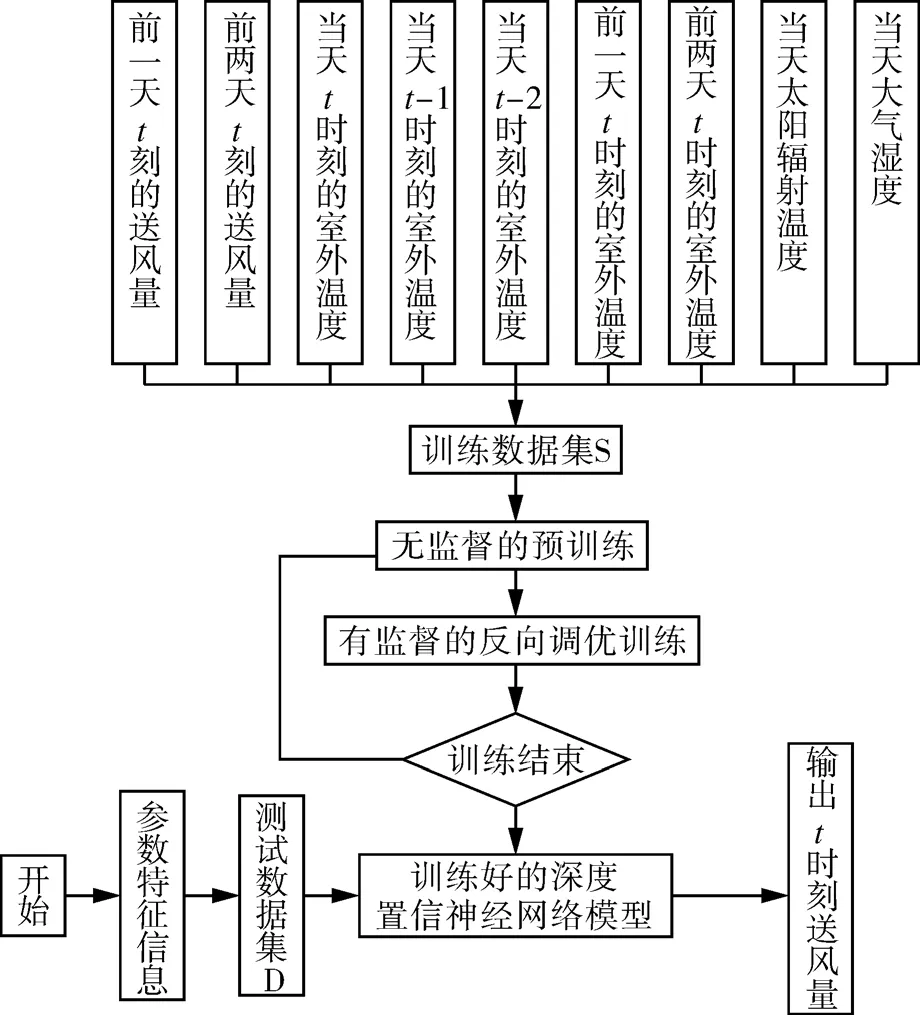
圖4 基于DBN的變風量空調送風量的預測流程Fig.4 Prediction process of supply air volume of VAV airconditioning based on DBN

2 試驗驗證

為驗證預測模型的有效性和精準性，對廣西某文化體育中心的室外氣象參數和大型變風量空調的送風量進行數據采集，室外氣象參數和建筑參數見表1。

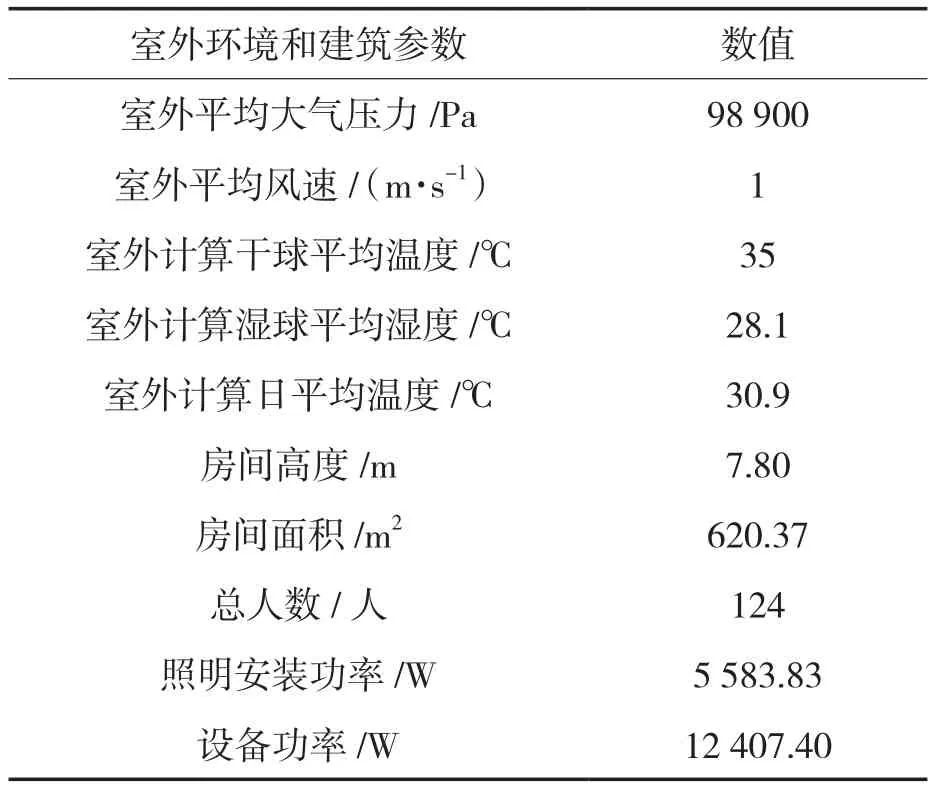
表1 室外氣象參數和建筑參數Tab.1 Outdoor weather parameters and building parameters

本文使用溫濕度自記錄儀、黑球溫度計和暖通空調電子風量測量儀FLY-1對文化體育中心大廳的室外氣象參數和VAV送風量進行測量，測量儀器的參數見表2。

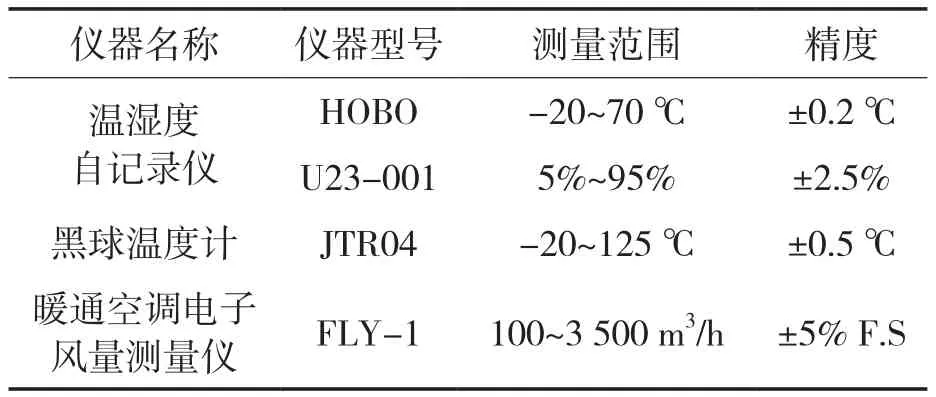
表2 測量儀器型號及參數Tab.2 Models and parameters of measuring instruments

在2019年6月中旬至2019年9月中旬期間，將3臺測量儀器設置為每10 min自行記錄一次，對記錄的數據進行整理，并剔除異常數據，收集1 000組數據做為訓練樣本。在2019年9月16日至18日3天內，將3臺測量儀器設置為每1 h自行記錄一次，收集13組數據做為預測樣本，根據9月16日和17日2天的VAV逐時送風量和室外逐時溫度的實測數據與9月18日的室外氣象參數，運用神經網絡模型預測9月18日9：00～21：00的 VAV逐時送風量，并和實測值進行比較。

為驗證DBN模型的預測性能，本文又構建了BP神經網絡預測模型、Elman神經網絡預測模型和模糊神經網絡預測模型共3種傳統神經網絡模型，將DBN模型的預測精度與3種傳統神經網絡模型的預測精度進行對比。

將訓練樣本數據集S分別導入到BP、Elman、模糊神經網絡和DBN模型中，訓練結束后，將測試數據集D所對應的VAV送風量進行預測。圖5～8分別為 BP、Elman、模糊神經網絡和 DBN 模型預測結果與實際值的對比，從圖中可知，BP、Elman和模糊3種模型的預測結果與實際值存在一定偏差，而DBN模型相較于以上3種傳統神經網絡模型能夠較好的與實際值吻合。為了更加清晰直觀地看到4種神經網絡模型的預測精度，將BP、Elman、模糊和DBN模型的預測誤差進行對比，如圖9所示。從圖9中，DBN模型的預測誤差最小，波動相較于BP、Elman和模糊神經網絡模型來說更為平緩，預測效果最好。

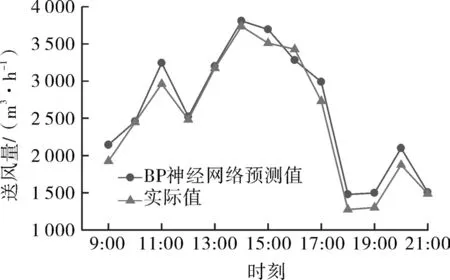
圖5 BP神經網絡預測值與實際值的對比Fig.5 Comparison of predicted values of BP neural network and actual values

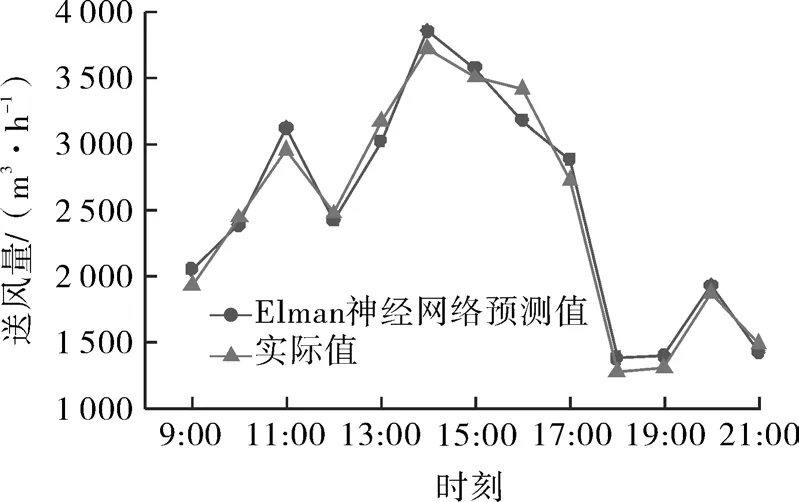
圖6 Elman神經網絡預測值與實際值的對比Fig.6 Comparison of predicted values and actual values of Elman neural network

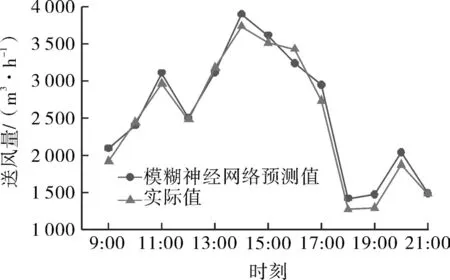
圖7 模糊神經網絡預測值與實際值的對比Fig.7 Comparison of predicted values and actual values of fuzzy neural network

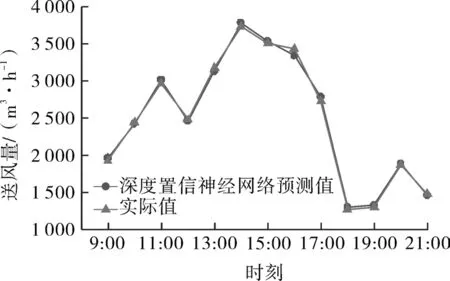
圖8 深度置信神經網絡預測值與實際值的對比Fig.8 Comparison of DBN predicted values and actual values

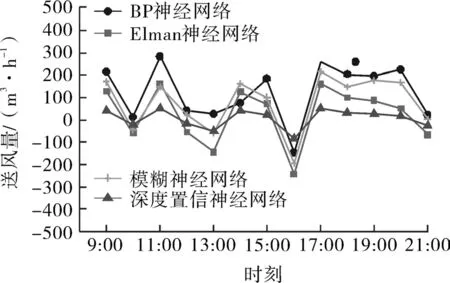
圖9 BP、Elman、模糊和DBN模型預測誤差的對比Fig.9 Comparison of prediction errors of BP，Elman，fuzzy and DBN models

為進一步評估DBN和淺層神經網絡模型預測VAV送風量的性能，采用平均絕對相對誤差（MAPE）、均方根相對誤差（RMSPE）和決定系數（R2）來評估各個模型的預測性能［16-18］。

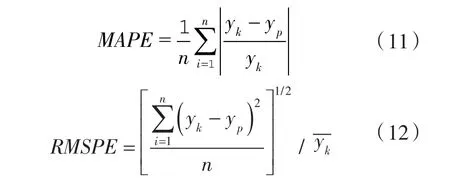
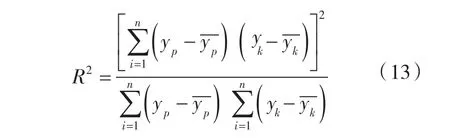
式中 yk，yp——實際值和預測值；

通常MAPE的值越小表明預測性能越好。RMSPE是預測過程中較好的一個指標，RMSPE的值越小，表明預測值和實際值的偏差越小，預測性能越好。R2是一個預測精度的有效指標，R2值越大，表明預測值與實際值之間的線性關系越高。表3為4種模型的MAPE、RMSPE和R2值，由表3可知，DBN模型的MAPE值和RMSPE值最小，R2值最大，由此說明相較于BP、Elman和模糊神經網絡，DBN模型具有更高的預測精度和穩定性。模型具有更高的預測精度和穩定性。

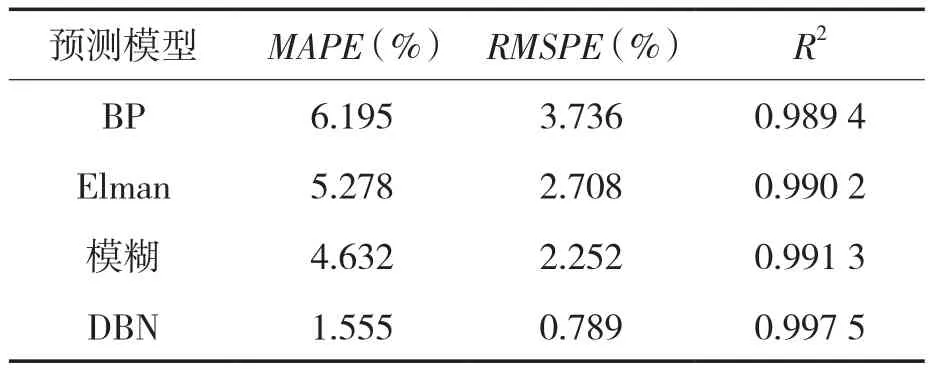
表3 BP、Elman、模糊和DBN模型的預測性能Tab.3 Predictive performance of BP,Elman,fuzzy and DBN models

3 結語

根據變風量空調送風量的影響參數，建立基于深度置信神經網絡的變風量空調送風量的預測模型。通過對某大型變風量空調的送風量和室外氣象參數進行數據采集，將實測數據導入到DBN模型以及BP、Elman和模糊3種傳統神經網絡模型進行預測。結果顯示，DBN模型的平均絕對相對誤差、均方根相對誤差和決定系數分別為1.555%、0.789%和0.997 5，因此，DBN模型在預測變風量空調逐時送風量時，相較于傳統的神經網絡模型，該模型能夠穩定、準確地預測逐時送風量，避免了傳統神經網絡由于容易陷入局部收斂而導致出現波動較大和過擬合的問題，故 DBN模型在預測變風量逐時送風量時具有全局穩定和較好的預測性能，與傳統神經網絡的計算精度相比具有明顯的優勢。