區域干旱重現期反演研究

徐 敏

( 遼寧省本溪水文局，遼寧 本溪 117000)

干旱頻率分析是干旱風險劃分的重要基礎和內容，對干旱風險普查至關重要[1]，也是對干旱發生和影響程度的重要評定依據，干旱重現期通過干旱頻率反演，對干旱條件下水資源高效利用具有重要的意義[2]。早期干旱事件主要是針對區域內干旱發生及持續的時空特征上進行單維變化分析[3- 5]。為了解決單一維度干旱變量不能有效反演干旱遷移變化規律的問題，基于干旱強度、持續時間、間隔時段等多變量的干旱頻率分析得到一定程度的研究[6- 9]。在這些成果中，Copula函數可克服傳統單變量分析方法的不足[11]，在國內一些地區干旱頻率分析中得到應用和推廣[10- 12]。近些年來。受人類活動和氣候變化的綜合影響。阜新地區近些年來發生嚴重干旱事件的頻次逐年增高，且存在多發頻發的演變態勢[15]。為有效應對區域干旱變化，制定有效的抗旱措施，將傳統被動抗旱轉為主動防御旱情，需要對干旱發生頻率及干旱風險進行綜合分析。為此本文基于Copula函數，以干旱特征兩個重要影響指標為依據，建立其聯合概率模型，對區域干旱重現期進行重構反演分析。研究成果對于阜新地區干旱演變特征以及干旱風險具有重要的參考意義。

1 干旱重現期計算方法

結合干旱歷時和干旱烈度雙變量聯合概率以及各單量概率可分析，干旱歷時和干旱烈度分別大于d和s時，或者其同時大于d和s時的干旱頻率計算方程為：

P(D>d)=1-P(D≤d)=1-FD(d)P(S>s)=1-P(S≤s)=1-FS(s)P(D>d，S>s)=1-FD(d)-FS(s)+FD，S(d，s)

(1)

式中，P—干旱頻率;FD—干旱歷時累積概率分布函數；FS—干旱烈度累積概率分布函數；FD,s—干旱烈度和干旱歷時累積概率分布函數；D—干旱歷時統計變量，d；S—干旱烈度統計變量；d—發生某一程度干旱事件的干旱歷時，d；s—發生某一程度干旱事件的干旱烈度。

一年中干旱事件可能發生1次，也可能多次發生，因此干旱重現期分析不適合采用設計洪水重現期的計算方法。干旱歷時D和干旱強度S大于或等于某一數值的重現期為：

TD=T(D≥d)=E(L)/P(D>d)Ts=T(S≥s)=E(L)/P(S≥s)

(2)

式中，TD—干旱歷時重現期，d；Ts—干旱強度重現期，d；E(L)—干旱持續時間與未發生干旱歷時的兩個干旱特征變量期望值相加，d。

干旱重現期的計算以同時表征干旱烈度和干旱歷時的可能度，與單變量重現期計算方法不完全等同。干旱烈度和干旱歷時同時考慮時其干旱重現期TDs計算方程為：

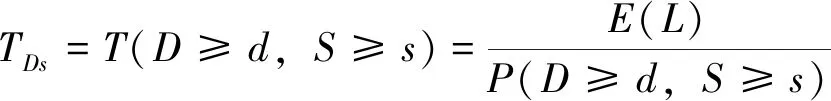
(3)

方程中,TDs—干旱歷時和干旱強度聯合分布的重現期，d；T—重現期，d。

2 旱評估指標選取

分別選用降水距平百分率Pa、標準化降水指數SPI和Z指數作為干旱評估指標，對阜新地區干旱指標適用性進行評估。各干旱指標時間計算尺度為1個月。阜新地區各縣區干旱指標識別結果見表1。

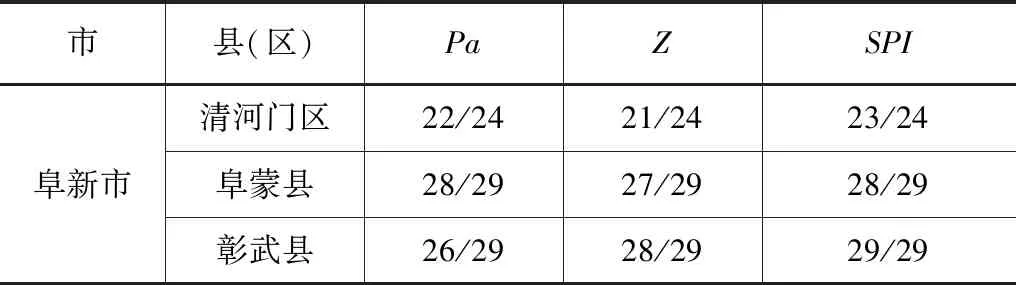
表1 阜新市各縣區干旱指標識別結果對比

由表1可見，對于各縣區來說，1個月尺度的SPI、Pa以及Z指數的干旱識別結果各有不同，其中SPI在月尺度干旱識別誤差均可低于5%，具有較好的識別精度。為此，將1個月尺度的SPI作為研究區域干旱事件識別指標，并據此進行干旱頻率計算。

3 干旱特征變量提取

在區域干旱事件識別的基礎上，對其干旱樣本數據系列進行獲取，對于符合干旱特征的變量樣本序列需要進一步定量和客觀表述。干旱歷時和烈度可用來表征干旱特征變量。干旱歷時是指某一場次干旱事件過程的持續時間，用于定量描述干旱事件的時間特征。依據游程理論，識別結果的橫軸跨度即為干旱歷時。干旱烈度是指某一場次干旱事件的累積水分虧缺程度，體現為閾值指標與干旱指標之差的累積和，用于定量描述干旱事件的嚴重程度。即下圖歷時干旱指標SPI與閾值之差的累積值來計算。阜新地區干旱事件識別結果見表2，并基于1個月尺度SPI對阜新地區干旱特征便利進行系列統計，統計結果見表3。

表2 阜新市干旱事件識別結果

表3 基于1個月尺度SPI指標的阜新地區干旱特征變量系列統計結果

基于表3阜新地區干旱特征變量系列統計結果分析可知，近30年間，基于1個月尺度SPI指標識別的阜新地區縣區的干旱事件數在20～50次，與抗旱統計報表的數據相近。各縣區平均干旱歷時在6—9月之間，總的來彰武縣和阜蒙縣具有相對較長的干旱歷時均值以及相對較大的干旱烈度均值，清河門區具有相對較短和相對較小的平均干旱歷時和平均干旱烈度。

4 干旱特征變量特征變量聯合頻率分析

傳統多變量概率分析模型假設具有相互獨立的變量，各獨立變量邊緣概率相乘即為其聯合分布概率，或者假設各變量邊緣概率處于同分布，變量聯合分布表達式為顯式。但是由于干旱烈度和干旱歷時之間存在顯著關聯性，且變量概率分布均不相同，因此需要采用不同類型概率分布函數進行聯合概率分布分析。為此本文結合Copula多函數，基于阜新地區干旱歷時和干旱烈度分析數據作為干旱特征雙變量進行干旱聯合頻率分析，分析結果見表4，并對其聯合概率分布進行了分析，如圖1所示。

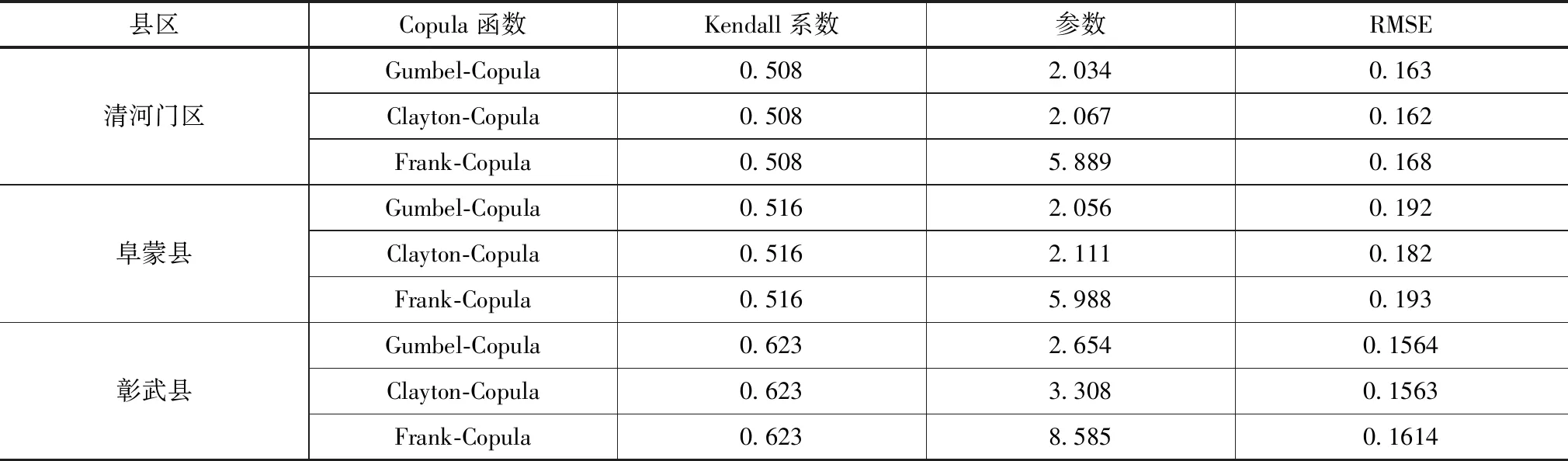
表4 基于RMSE的Copula函數最優選擇

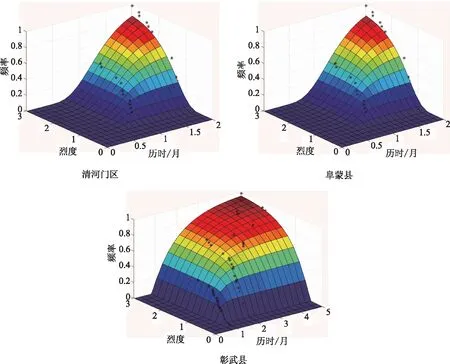
圖1 阜新縣區干旱聯合概率分布曲線

從分析結果可看出，清河門區不同類型干旱聯合概率分布Copula函數的Kendall相關系數均高于0.5，Clayton-Copula的均方根誤差RMSE值在各類型函數中最低，為0.162，其擬合結果也優于其他函數，相比于其他兩類函數更適合于清河區干旱聯合頻率分布特征，其聯合干旱頻率分布函數為

式中，C—干旱頻率分布函數；cl、μ、ν、θ—函數參數。

阜蒙縣不同類型干旱聯合概率分布Copula函數的Kendall相關系數也均高于0.5，總體而言Clayton-Copula函數的方根誤差RMSE值在各類型函數中最低，擬合度更好，其函數為

從彰武縣各類型分布函數的Kendall相關系數可看出，其相關系數高于0.6，Clayton-Copula函數擬合度最高，方根誤差RMSE值最低，其分布函數為

從阜新地區干旱聯合概率分布函數可看出，Clayton-Copula為該區域干旱頻率最優概率分布函數。

5 干旱重現期分析

通過對干旱及烈度聯合頻率的分析，計算得到阜新地區的干旱重現期，結果見表5。

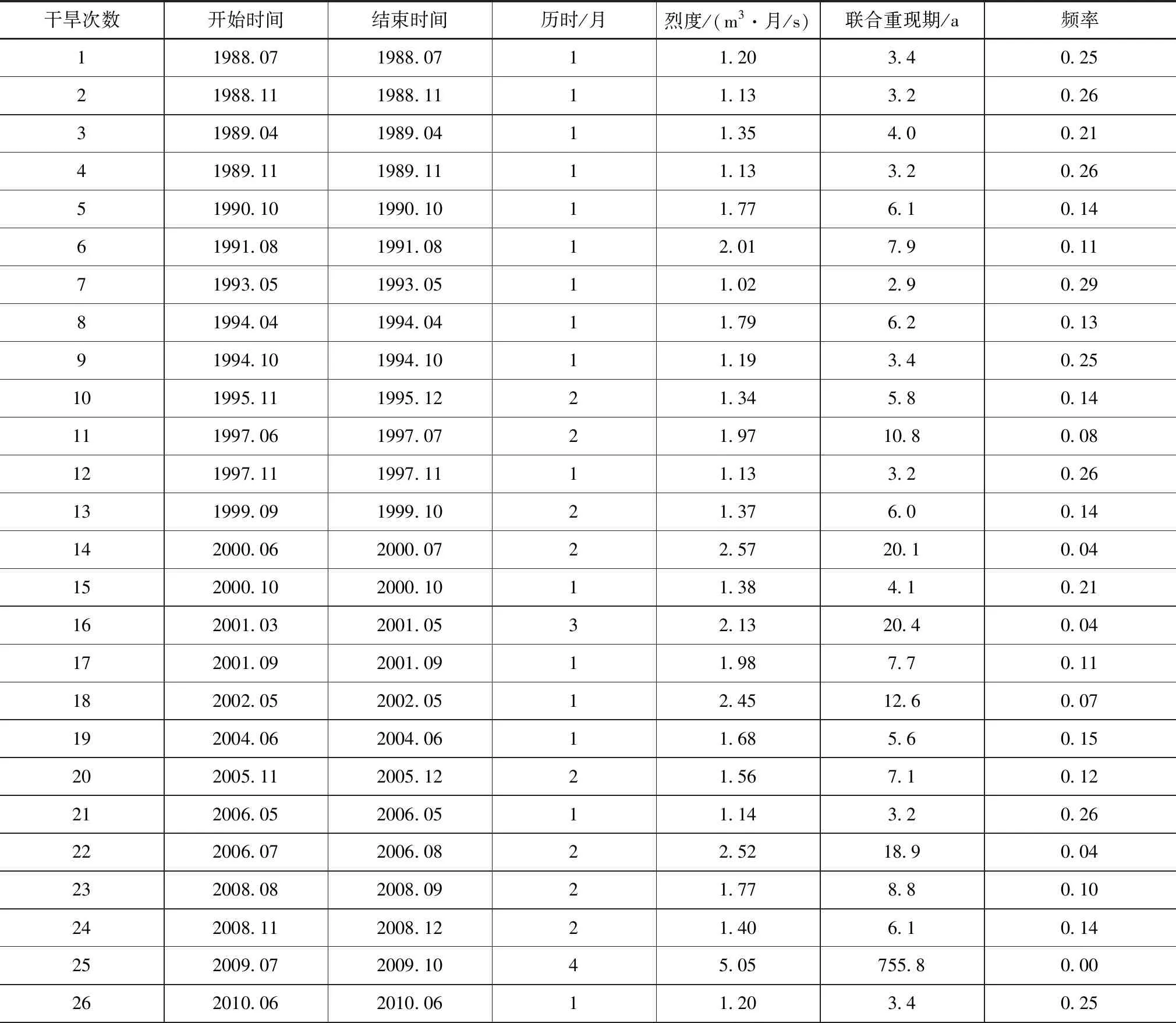
表5 阜新地區的干旱重現期分析結果

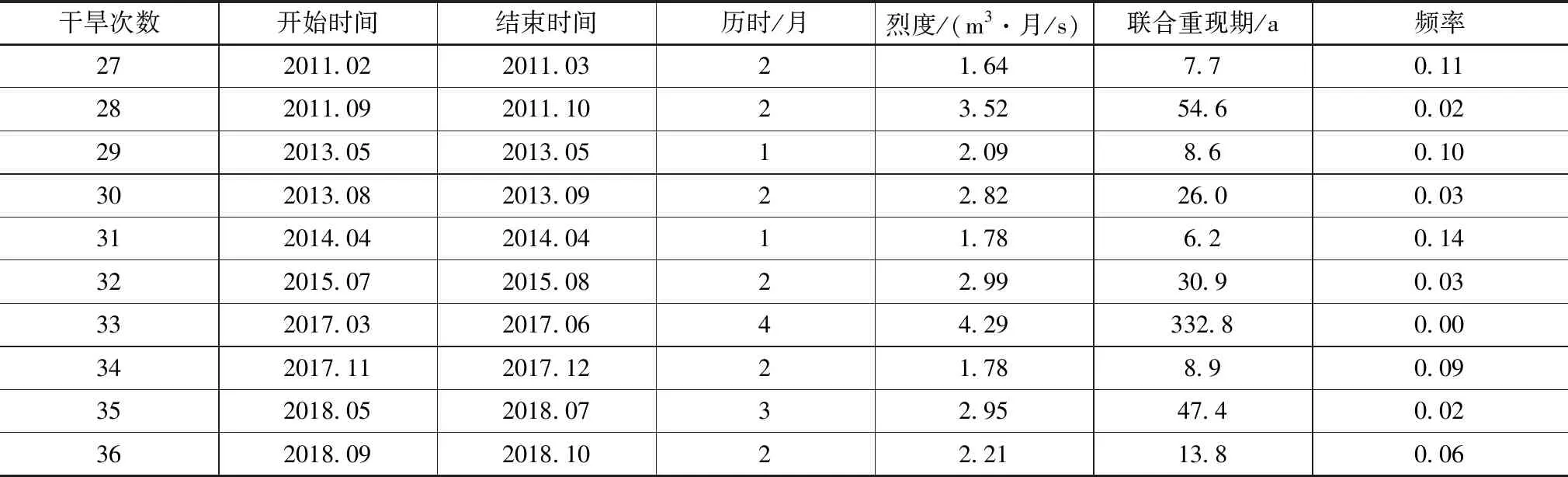
(續表5)

干旱重現期主要表示在長時段內每平均出現一次超過或等于某一量級干旱事件所間隔的歷時，一般以年為計算時間。干旱重現期和干旱頻率存在定量聯系。干旱重現期相比于干旱頻率可綜合反映干旱事件隨機性更便于抗旱減災實際工作中發布具體旱情信息。此外需要說明的是如百年一遇干旱不應被認為相隔100年出現一次干旱事件，這種干旱量級從概率論角度出發其在100年內出現的頻次可能超過1次，也可能出現的頻次為0。

6 主要結論

(1)在Copula三種主要類型函數中，Clayton-Copula函數擬合結果最優，因此在采用Copula函數進行干旱歷時-烈度干旱聯合概率分析時，建議主選Clayton-Copula函數作為其擬合函數。

(2)在進行干旱事件指標識別時，為更好的反演區域干旱變化特征，建議以不同干旱指標識別誤差低于5%為控制指標，選取誤差較低的指標進行干旱事件識別。

(3)干旱重現期和干旱頻率存在相互對應關系。干旱重現期相比于干旱頻率可綜合反映干旱事件隨機性，相比于干旱頻率更適合于抗旱減災實際工作中具體旱情信息的發布。