頁巖氣旋轉式井壁取心器轉向機構設計與優化*

朱維兵 龐青松 張朝界

(1. 西華大學 2. 四川航天烽火伺服控制技術有限公司)

0 引 言

在頁巖氣的勘探開采過程中，取心是核心技術之一。川渝地區頁巖層經歷了強烈的后期改造，地質條件相對復雜，頁巖分布不穩定，呈現較強的各向異性特征。頁巖氣井水平段長達1 000～2 000 m，常規的鉆桿和連續管送入方式難以將取心儀器準確下入到取心位置，且鉆完井工作難度高、耗時長、花費大。針對川渝地區頁巖氣長水平段取心困難問題，筆者所在研究團隊首次將井下爬行器與旋轉式井壁取心儀器相結合，設計了一種集爬行、定位、推靠、取心、儲樣和解卡等功能于一體的頁巖氣旋轉式井壁取心器。該取心器采用模塊化設計，可完成水平井和大位移井的長水平段取心作業[1]。轉向機構作為頁巖氣旋轉式井壁取心器各模塊的連接轉向裝置，其性能決定了整個取心器的過彎通過能力。

現役的轉向機構主要有剛性和柔性兩種連接方式。柔性轉向機構運動時雖有一定的減震能力，但是運動具有不穩定性，不適用于本取心器；剛性連接轉向機構在作為固定聯軸器的同時，還提供傳動轉矩，整體結構穩定，可提高過彎能力。目前，剛性連接轉向機構主要采用3個自由度的球面轉動機構，雖然能夠繞3個方向轉動，但是軸向負載量偏小[2]。侯雨雷等[3]在剛性連接轉向機構的基礎上提出了3-PSS/S新型轉向機構，該轉向機構利用電機控制的滾珠絲杠提供動力，可以控制關節機構的轉動，也能承受軸向負載，但由于運動方式是直線，增加了整個機構的長度，而且采用電機控制，增加了控制成本[4]。邵宏政[5]申請的專利“萬向節連接裝置”采用剛性連接，能實現轉彎要求，但是容易傳遞震動等不利因素，而且在高溫高壓的石油井環境中一旦因為小零件松動而導致萬向節脫落，將推遲取心器的工作時間。蔣宇晨等[6]申請的專利產品采用空心橡膠桿作為上、下平臺的連接件，存在橡膠易老化、不耐高溫及使用壽命短等問題。高勝等[7]申請的專利“井下牽引器定位與連接機構”可以實現上、下平臺姿態的精準調整和控制，連接機構通過液壓缸驅動，不適用于下井時在造斜段連續爬行的要求。為此，筆者擬設計一種新型轉向連接機構，以期把取心器的各模塊有效地連接，并且有較為強勁的過彎能力，可防止卡阻現象。

1 頁巖氣旋轉式取心器總體方案設計

隨著近幾年對川渝地區頁巖油氣資源的勘測，其油氣井逐漸發展為具有1 000～2 000 m的長水平段，直徑150～300 mm的水平井。為了能夠順利進入水平井中完成取心工作，取心器長度需要控制在7 m左右，直徑小于150 mm；取心器在水平段爬行速度要大于560 m/h，以節省通過時間；負載能力要大，能夠克服井下阻力并運輸取心儀器進行工作；取心器在井下工作段深度達到3 000～4 000 m，井下壓力將達到60 MPa，溫度達到60～100 ℃，而且井下可能有多種物質混合的油漿，因此要求各機構具有一定的剛度且密封性能好。

取心器采用模塊化設計，由爬行短節、扶正短節、推靠鎖緊短節、轉向節、取心和液壓控制模塊等組成，總體方案如圖1所示。扶正短節由4對扶正臂提供扶正力以保證取心器的運動姿態；爬行短節由爬行輪提供驅動力帶動整個取心器前進，爬行輪呈對稱布置，可以有效規避障礙物；端部設置有電纜接頭及電路部分，用于控制取心器；推靠短節對稱布置，在取心儀器工作前，推靠短節負責將取心器推靠到井壁一側進行固定，在爬行過程中推靠短節處于未展開狀態存放于推靠節中；各模塊間用轉向節(轉向裝置)連接，能夠提高過彎能力，有效防止取心器出現卡阻現象。張朝界[8]使用Solidworks軟件模擬實際工況，建立了頁巖氣水平井和取心器的三維模型，利用ADAMS虛擬樣機仿真技術對整個取心器的爬行能力、過彎能力、負載能力和越障能力等進行了計算機模擬分析，結果均滿足設計要求。

鑒于篇幅原因，有關內容沒在本文中呈現，本文側重于介紹轉向連接機構的創新設計和過彎能力的優化設計。

1、9— 扶正短節；2、8—爬行短節；3、7—轉向節；4、6—推靠短節；5—取心儀器；10—電纜接頭。

2 轉向連接機構設計

2.1 方案選擇

因所設計的取心器是在水平井爬行器上集成了取心工具，整體較長，所以其軸向長度對井下過彎能力有很大的影響。采用串聯構成方式，雖然簡化了取心器的連接方式，但是增加了整體長度，不利于通過小曲率井；并且由于在過彎時有徑向轉彎和軸向的爬行負載，所以需要有徑向轉彎能力和一定的軸向負載能力。針對取心器在彎曲段的通過能力，筆者設計了一種新型轉向機構(見圖2)串聯在爬行短節和推靠短節之間，在取心器通過彎曲段時，利用轉向機構的可彎曲性，可以有效提高取心器的過彎能力；同時可以承受串聯機構的輕微彎曲和軸向負載能力。

該轉向機構由一個胡克鉸鏈中心連接，具有一定的軸向承載能力，同時還可以繞各方向旋轉；四周布置4組球面副，每個球面副的中心由移動副和彈簧連接。

圖2 轉向機構簡圖Fig.2 Schematic diagram of the steering mechanism

2.2 受力分析

在對轉向機構進行受力分析時，需要考慮兩種情況：一種是轉向節上端平臺和下端平臺平行時，上端平臺受到外部拉力，整個取心器保持直線狀態，四周的4對球面副在中心移動副鏈接的情況下沒有受到轉矩作用，僅為中心鉸鏈受到大小相同的拉力作用，受力如圖3a所示；另一種是轉向節有一定轉角，整個取心器處于過彎狀態，此時上端平臺受到外部拉力，四周的4對球面副在外部拉力作用下有一定轉向，導致移動副受壓或受拉而滑動，受力如圖3b所示。

圖3 轉向機構力學模型Fig.3 Mechanical model of the steering mechanism

圖3a中所受外載荷作用較為簡單，在此不作分析，這里主要對圖3b中的受力情況進行分析。將力簡化到中心鉸鏈上，表示為受到一定拉力F，利用拆桿法建立機構的靜力學平衡方程，考慮構件彈性，完成機構的靜力學分析[9-10]。將力F進行正交分解，然后使用拆桿法拆分轉向節各連接件，即可分別建立各構件的力平衡方程。當受到端面法向載荷時，轉向機構中心十字軸受力較大，周圍滑塊基本不受力，此時只需要對十字軸進行受力分析即可；當受到端面載荷為轉矩時，4個滑塊都有受力，此時受力較為復雜。但由于本轉向機構主要承受載荷力，不傳遞取心器的轉矩，所以在進行受力分析時只需要考慮外載荷為純力的情況。

當受到端面法向載荷時，十字軸及兩組軸頸上的受力情況如圖4所示。

由靜力學平衡原理有：

(1)

式中：Fox、Foy、Foz分別為拉力F的分力，N；Fi1、Fp2、Fq3分別為軸頸所受力的分力，N。

2.3 彈簧選型

由于在轉向節的移動副中，彈簧主要起支撐滑塊的作用，不傳遞軸向拉力和徑向轉矩，所以只需要選擇普通壓縮彈簧即可。查詢機械設計手冊[11]，并根據支鏈滑槽深度及大小，選擇彈簧參數如表1所示。

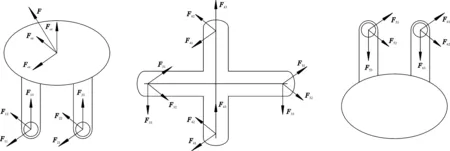
圖4 轉向機構各零件受力圖Fig.4 Force diagram of each part of the steering mechanism

表1 彈簧基本參數Table 1 Basic parameters of spring

3 轉向機構過彎優化設計

3.1 工作空間分析

轉向機構屬于空間支鏈結構，每個支鏈具有一定的空間轉向能力，在取心器過彎時可以使機構有一定的折彎效果，提高過彎能力，但是這些支鏈的相對運動可能會發生干涉，導致轉向機構在空間上因為干涉而出現卡阻現象，破壞取心器的轉向能力，所以需要對轉向機構進行空間幾何干涉分析。將轉向機構中間十字軸中心點設定為坐標原點，端面法向為Z軸方向，OXY平面與下端平臺平行，建立三維坐標系。已知上端平臺距下端平臺高度為h，4對滑塊距中心點距離為r，則上、下端面平臺的空間坐標分別為：

(2)

(3)

已知轉向機構的上、下平臺法線可偏轉角度為λ，考慮到上端平臺在法線方向的可偏轉性，根據動靜平臺的坐標確定上端平臺的偏轉空間，該空間即為運動過程中的工作空間，如圖5所示。如果取心器在轉彎時超過此工作空間，則轉向節就會發生干涉現象導致取心器卡阻，因此需要避免此情況。

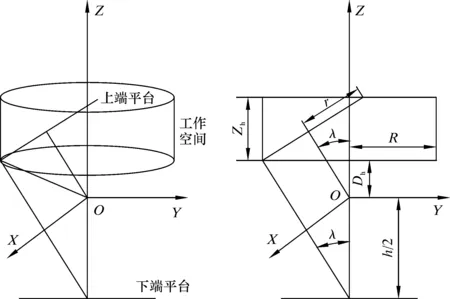
圖5 轉向機構運動幾何尺寸示意圖Fig.5 Schematic diagram of the movement geometry of the steering mechanism

由幾何關系可得：

(4)

(5)

式中：r是上、下端面半徑，mm；Zh是有效工作高度，mm；h是上、下端面平臺距離，mm；R是有效工作半徑，mm；λ為轉向節轉角，(°)。

聯立式(4)和式(5)，可得到工作空間的半徑函數關系及空間高度，其中高度表達式為：

Zh=2rsinλ

(6)

代入數據可得Zh=11.75 mm，R=48.86 mm。

根據計算的轉向機構工作空間及力學計算，可確定轉向裝置的整體尺寸及三維模型，如圖6所示，裝配簡圖如圖7所示。

圖6 轉向裝置三維模型Fig.6 Three-dimensional model of the steering device

1—螺紋端蓋；2、4—球鉸鏈；3—壓縮彈簧；5、6、8、9—工作平臺；7—十字軸。

3.2 過彎能力提升分析

取心器在到達水平井前，需要經過一個有一定曲率半徑的造斜井，由于取心器的長度特性，在經過造斜段時，其長度和外徑需要達到一定的要求才能通過，所以必須對取心器的過彎能力進行分析，普通取心器過彎能力示意圖如圖8所示。

圖8 取心器過彎能力示意圖Fig.8 Schematic diagram of the bend pass capability of the coring device

由幾何關系可得：

(7)

式中：LZ為取心器軸向長度，mm；RQ為造斜段的曲率半徑，mm；d為取心器直徑，mm；D為井徑，mm。

對式(7)進行化簡，得到取心器直徑的函數關系式：

(8)

造斜段轉角為：

(9)

式(8)即為取心器軸向長度與井徑D及曲率半徑RQ的函數關系。當取心器直徑d=90 mm時，相關結果如表2所示。

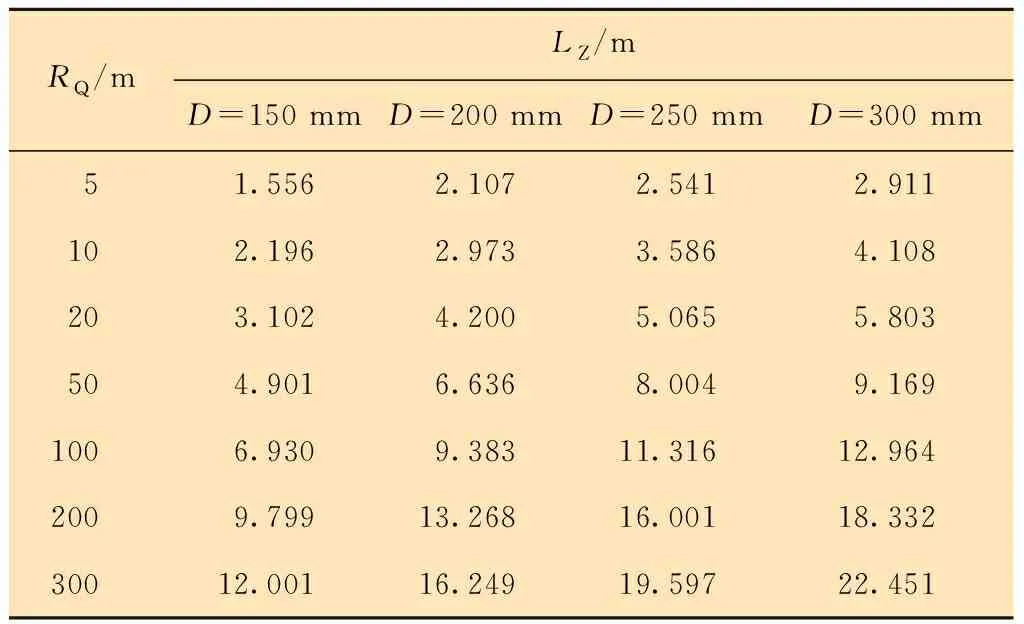
表2 取心器軸向長度與曲率半徑的關系Table 2 The relationship between the axial length of the coring tool and the radius of curvature

取心器軸向尺寸、曲率半徑和水平井井徑的相互關系如圖9所示。由圖9可知：在相同條件的水平井井徑下，曲率半徑與取心器能夠通過的長度呈正相關關系；由表2可以看出：在相同曲率半徑下，井徑與取心器可通過的長度也呈正相關關系；在沒有轉向節模塊時，取心器在小井徑曲率井(RQ=5 m，D=150 mm)中的有效通過長度僅有1.556 m；在曲率半徑達到50 m時有效通過長度為4.901 m，這遠遠達不到取心器的軸向長度要求。

圖9 取心器軸向尺寸、曲率半徑和水平井井徑的相互關系Fig.9 The relationship between the axial size of the coring tool and the radius of curvature

經過分析對比，取心器在集成取心工具的同時會增加長度，其總長度達到7.9～11.0 m，如果該取心器進入了小曲率半徑的水平井時，會發生卡阻現象而無法通過曲率井段。因此，采用模塊化方式優化取心器，取心器被轉向機構分為前、中、后3段，相鄰兩段由轉向機構連接，則優化后的取心器過彎能力示意圖如圖10所示。

圖10 優化后的取心器過彎能力示意圖Fig.10 Schematic diagram of the bend pass capacity of the optimized coring tool

圖10中：L1、L2、L3分別為取心器前、中、后3段長度，mm；λ1、λ2為不同井段轉向節轉角，(°)；L′為優化前爬行器前段軸向長度，mm；α′為造斜井段轉角，(°)。

由圖10可以看出，優化后爬行器前段正在通過曲率段，中間段剛好進入造斜段，后段還處于豎直井狀態，可見在通過相同曲率井段情況下，優化后的取心器有效長度增加了，并且3段長度L1、L2、L3的大小對可通過性都有較大的影響。

由幾何關系分析，可得到取心器長度的幾何函數關系：

(10)

(11)

將原爬行器總長度平分為3段，由圖10可知，3L′=3L2=LZ。已知爬行器前段和后段為對稱的爬行扶正結構，其長度相等，即L1=L3，則爬行器總長度LP=2L1+L2，轉向節轉角λ1=λ2=λ。保持爬行器及水平井管條件D、d、RQ與優化前爬行器尺寸一致。整理式(10)和式(11)可以得到取心器長度的函數關系式，計算出取心器的最大通過長度范圍，結果如表3所示。

表3 優化后取心器軸向長度與曲率半徑的關系Table 3 The relationship between the axial length of the coring tool and the radius of curvature after optimization

表3是有轉向節的取心器在相同曲率半徑井中最大通過長度。從表3可以看到，取心器在曲率半徑為20 m、井徑為150 mm時有效通過長度為10.358 m(優化前僅為3.102 m)。已知取心器所需總長度為7 m左右，說明優化后爬行器可通過曲率半徑為20 m、井徑為150 mm的彎曲井。

將優化前、后取心器軸向長度與曲率半徑做對比，可得到如圖11所示的關系曲線。

圖11 優化前、后取心器軸向長度與曲率半徑的關系Fig.11 The relationship between the axial length of the coring tool and the radius of curvature before and after optimization

從圖11可以看出，優化后取心器可通過長度大大增加，整體趨勢呈上升狀態，且各井徑下的可通過長度均比優化前大，說明轉向節可大大增強取心器的過彎能力。

4 結 論

(1)根據取心器的工作要求，設計了一種新型連接轉向機構。該機構具有一定的減振效果，可以減小不同短節振動的相互影響，減小振動噪聲對設備的干擾，緩沖一定程度的振動沖擊。

(2)在相同條件的水平井徑下，曲率半徑與取心器能夠通過的長度呈正相關關系；在相同曲率半徑下，井徑與取心器可通過的長度也呈正相關關系。在沒有轉向節模塊時，取心器在小井徑曲率井(曲率半徑=5 m，井徑150 mm)中的有效通過長度僅有1.556 m；在曲率半徑達到50 m時有效通過長度為4.901 m，這遠遠達不到取心器的軸向長度要求。

(3)以通過能力最大為優化目標，對取心器的模塊化尺寸進行優化，當曲率半徑為20 m、井徑為150 mm時有效通過長度為10.358 m(優化前僅為3.102 m)，遠遠超過取心器軸向長度7 m的要求，說明優化后取心器能夠通過曲率半徑為20 m、井徑為150 mm的水平井。優化后取心器可通過長度大為增加，整體趨勢呈上升狀態，且各井徑下的可通過長度均比優化前大，說明轉向裝置可大大增強取心器的過彎能力。