比特級碼率兼容多元LDPC碼打孔算法*

周 華，錢荷玥，王登天，葛旗偉

(南京信息工程大學 電子與信息工程學院，南京 210044)

0 引 言

近20年來，糾錯編碼技術快速發展。20世紀末，Mackey等人[1]的發現迎來了低密度奇偶校驗碼(Low-density Parity-check，LDPC)碼的研究熱潮。而后人們發現多元LDPC(Non-binary LDPC，NB-LDPC)碼與碼長碼率近似的二元LDPC碼和Turbo碼相比，在中短碼情況下其譯碼性能具有較大增益[2]。如何發揮NB-LDPC碼的優勢也成為了通信領域值得關注的研究課題。

ITU在移動通信的技術標準中將碼率兼容(Rate-compatible，RC)技術確立為核心技術之一，可見實現信息傳輸速率的可變性已經成為現代通信領域不可或缺的功能之一。其中，碼率兼容技術是實現信道編碼多重碼率的重要手段，通信系統在采用碼率兼容碼時，可根據當前信道的狀態調整碼率，確保信息傳輸的有效性和可靠性。

LDPC碼由其特定的校驗矩陣定義，碼長和碼率受校驗矩陣的大小限制，在信息傳輸過程中存在著碼率不夠靈活的缺點。基于這個問題，Hagenauer[3]在1988年首次提出了碼率兼容的打孔型卷積碼，通過對編碼之后的卷積碼(母碼)進行打孔，得到了一系列高碼率的子碼，有效解決了變碼率的問題，但打孔位置的選擇比較復雜且直接影響譯碼性能。21世紀初期，Ha等人[4-5]對二元LDPC進行了碼率兼容的研究，實現了二元LDPC從低碼率到高碼率的自由切換。相較于二元碼率兼容LDPC(RC-LDPC)碼[6-7]，多元碼率兼容LDPC(NB-RC-LDPC)碼的研究在國際上相對較少。2008年，Klinc等人[8]第一次對多元LDPC碼在碼率兼容方面進行了研究。2011年，Zhang等人[9]通過將二元打孔方案引入多元打孔，構造了一組基于小環路的多元RC-LDPC碼。2016年，Deka等人[10]研究了多元矩陣的短環路并結合環外信息度(Extrinsic Message Degree，EMD)的打孔方案。2018年，穆錫金等人[11]通過掩模矩陣和基矩陣的優化擴展了多元碼，得到了一系列碼率降低的多元RC-LDPC碼。

本文針對多元RC-LDPC碼在打孔算法中各碼率譯碼性能不足的問題，提出了一種基于比特級的新型多元打孔算法。該算法將多元LDPC碼的打孔節點的選擇從符號級擴展到了比特級，并結合多元二進制鏡像矩陣的度分布選取較優的打孔變量節點，實現了低碼率向高碼率之間的轉換。仿真驗證了該算法的有效性，所構造的NB-RC-LDPC碼在較大的碼率范圍內都能獲得較好的譯碼性能。

1 多元LDPC碼譯碼

與二元LDPC碼情況類似，一個M×N多元LDPC碼也由其稀疏校驗矩陣HNB={hij|i=0,1,2,…,M-1，j=0,1,2,…,N-1}的零域空間所定義，不同的是，HNB中的元素取自伽羅華域GF(q)(q=2m,m=1,2,3…)，即hij∈GF(q)[12]。多元LDPC碼與二元LDPC碼一樣在譯碼時采用傳統置信傳播(Belief-Propagation,BP)算法，置信信息在變量節點與校驗節點之間交互傳遞，二元BP譯碼算法傳遞的是單比特信息，多元BP傳遞的是由多個二進制比特信息構成的信息序列，即符號信息。

一個定義在GF(q)上的多元LDPC碼，其校驗矩陣為

該矩陣的Tanner圖如圖1所示，可用G={(V，E)}表示，其中V=Vv∪Vc，Vv=(v0,v1,…,vN-1)是變量節點的集合，對應于校驗矩陣的列；Vc=(C0,C1,…,CM-1)是校驗節點的集合，對應于校驗矩陣的行；E是所有連接變量節點和校驗節點邊的集合。每一條邊對應校驗矩陣中的非零元hij，與節點相連的邊的個數稱為節點的度(degree),行重和列重分別表示校驗節點和變量節點的度數。

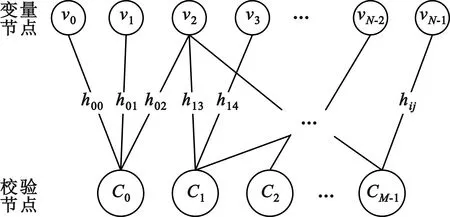
圖1 多元LDPC碼Tanner圖

一個長度為N的向量c,其中c=(c0,c1,c2,…,cN-1),cn∈GF(q),如果滿足式(1)，則認為向量c為合法碼字。

c·HNBT=0。

(1)

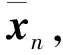
(2)

(3)

多元碼字的一個碼元由m個二進制比特組成，在譯碼過程中，碼字中的一個比特或是多個比特出現錯誤，譯碼器都將這個碼字看作譯碼失敗，這使多元LDPC碼具備了更好的抗突發噪聲的性能[13]。另外，多個比特組成一個碼元，在編譯碼環節碼字一次運算m個比特，很大程度上提高了編譯碼的效率。

2 多元打孔算法

目前，打孔算法是實現LDPC碼碼率兼容的主要方式之一。打孔算法的含義是通過對部分變量節點作刪余處理，從而提高碼率。“刪余”不是刪除對應的碼元，是對選定的校驗位信息不進行傳輸。由于接收端在打孔位無法獲取有用信息，故譯碼性能下降。因此多元LDPC碼的打孔算法的關鍵是找出對譯碼性能影響較小的變量節點，從而盡可能降低性能損耗。

隨機打孔算法是目前實現碼率兼容的常用方式之一，一個低碼率的LDPC母碼隨機選擇不需要傳輸的碼元位置，構造高碼率的子碼。對于一個碼長為N、信息位長度為K(K=N-M)的滿秩多元LDPC母碼，其碼率為R=K/N。若目標碼率為R′(R′>R),則需要刪余的變量節點個數約為

(4)

多元LDPC碼在傳輸時，首先將多元碼字轉化成二進制，即多元符號轉化成比特序列[12]。在選擇打孔節點時，根據目標碼率R′，需要對MR′個符號節點或者(MR′×m)個比特節點進行刪余。圖2展示了符號級打孔與比特級打孔兩種打孔類型。

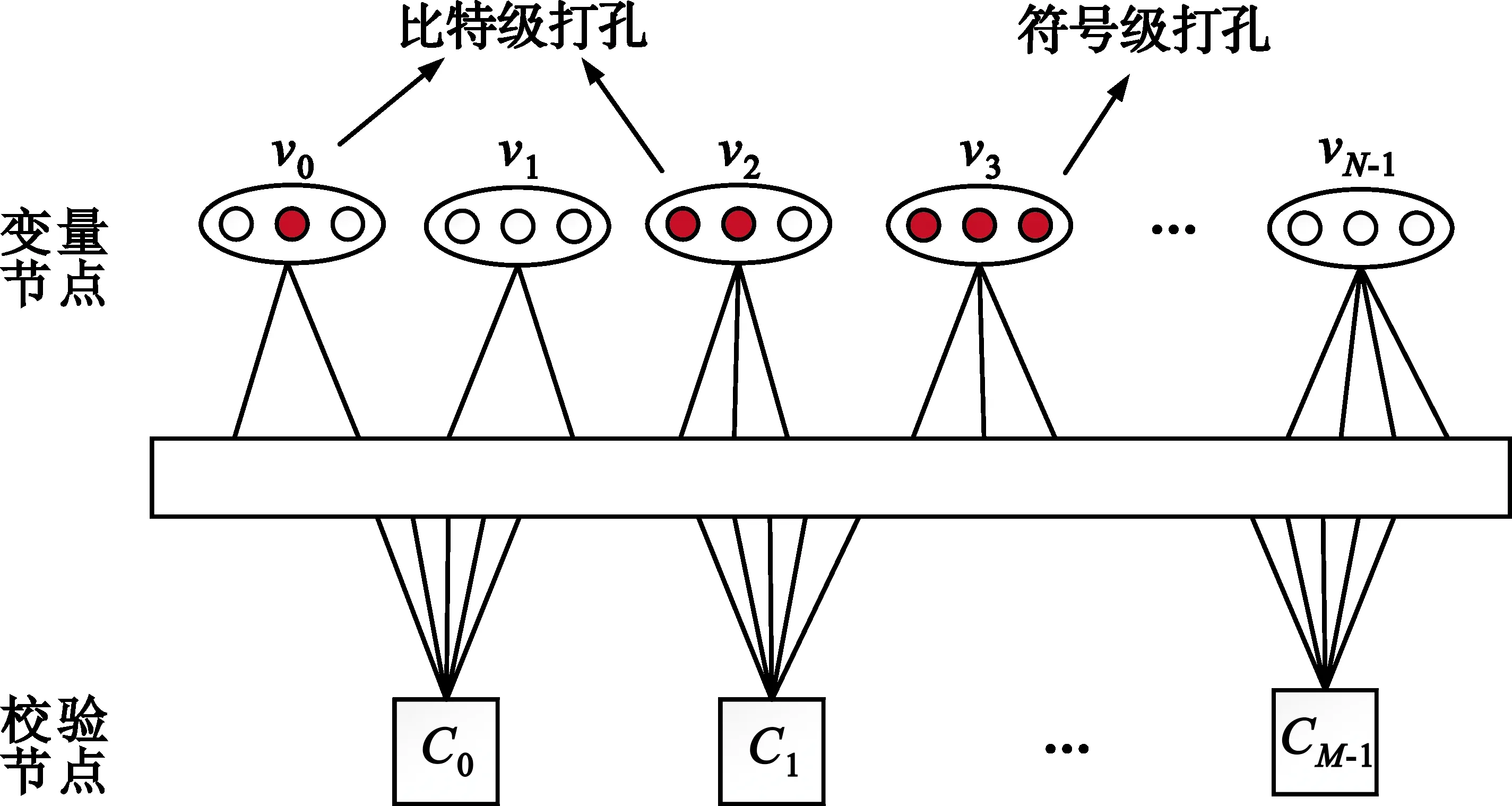
圖2 多元LDPC碼打孔

在多元打孔算法中會出現兩種情況，其中一種與二元打孔類似，某個變量節點的信息全部刪余，即圖2中v3的情況，通常稱這一類打孔算法為符號級打孔。另一類即在比特向量進行處理，選擇合適的比特節點進行刪余，但仍保留比特向量中某些比特信息進行譯碼傳輸，類似圖2中v0和v2的打孔類型，稱這一類算法為比特級打孔[14]。相較于符號級打孔算法，比特級擁有更多的可選擇性，因此本文基于比特級碼元提出了一種新型打孔算法。

3 多元比特級打孔算法

在介紹本文多元打孔算法之前先介紹二進制鏡像矩陣的概念。

在伽羅華域GF(q)中，令α為GF(q)的本原域元素，f(α)是其本原多項式，則α的冪次可根據其本原多項式生成所有的非零元素，零元素可表示為全零多項式[15]。假設

f(α)=a0+a1x+a2x2+…+amxm。

(5)

式中：f(α)的最高次冪為m，系數a0,a1,a2…,am∈GF(2)。由α定義的伴隨矩陣是一個m×m的二元矩陣K：

矩陣K被稱為α在伽羅華域GF(q)的二進制鏡像矩陣。

根據上述概念可以將一個大小為M×N多元LDPC碼的校驗矩陣變為一個Mm×Nm的不規則二元鏡像矩陣。二元矩陣的每一列都對應著變量節點的某一個比特信息，為打孔操作提供了更多的選擇。根據表1所示的四元域內非零元素的多項式，可得到圖3和圖4，分別給出了2×3多元矩陣與其對應的二元鏡像4×6矩陣的關系圖及Tanner圖。

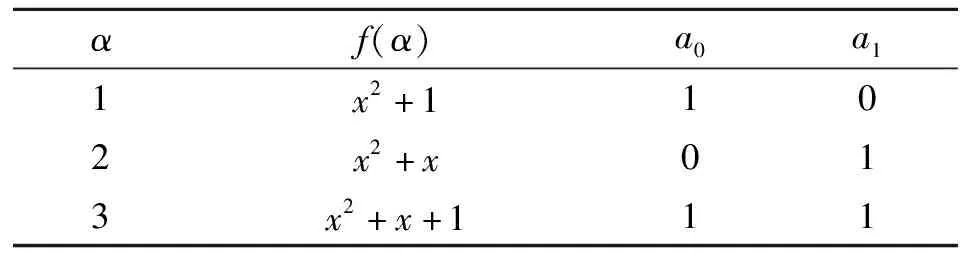
表1 四元本原多項式

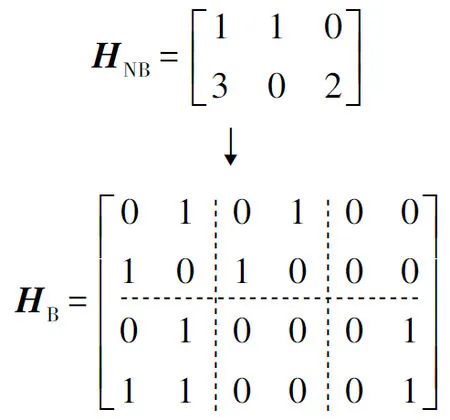
圖3 多元矩陣與其二元鏡像矩陣關系圖

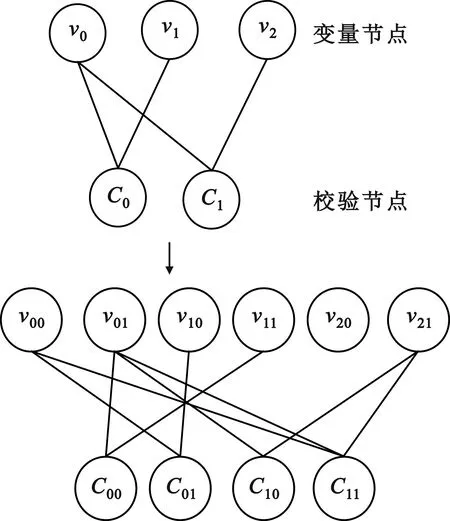
圖4 多元LDPC碼與二元LDPC碼的Tanner圖對比

在譯碼的過程中，列重大的列有助于譯碼時快速糾錯，對應列重小的列的碼元發生錯誤時，對相鄰節點的影響相對較小。在將多元矩陣轉化成對應的二元鏡像矩陣后，可以根據列重的大小即度數的大小來選擇合適的打孔變量節點。類似圖4中的v20在二進制鏡像處理后對譯碼性能影響最小，故在選擇比特節點時可選擇v20刪余，在保證性能的同時又提高了碼率。據此本文提出了一種基于比特級的非隨機打孔算法。對于特定的多元M×N矩陣HNB，根據其多元域的本原多項式轉化成Mm×Nm的二進制鏡像矩陣HB。計算HB中每個變量節點的度數，并將其按由大到小的順序放入集合G中，輸出集合中列重最小的打孔變量節點vab,其中a代表比特節點的符號位，b代表比特位。具體打孔流程如圖5所示。

圖5 基于比特級的新型打孔算法流程圖

比特級新型打孔算法為多元LDPC碼碼率兼容提供了更多的打孔選擇性，算法實質是優先選擇度數小的列所對應的變量節點進行刪余，從而提高譯碼性能。在選擇打孔節點個數時，所得到的MR′是基于符號級的，故在比特級打孔時需對MR′×m個比特節點進行處理。根據二元鏡像矩陣得到的一組比特打孔節點vab(0≤a≤N-1,0≤b≤m-1)，a對應于HNB中的符號位，b對應于符號中m個比特位。

4 仿真與分析

為了驗證該打孔算法的譯碼性能，仿真選用了碼長為155、碼率為0.4和碼長為576、碼率為0.5的規則四元LDPC碼，與傳統的多元符號級隨機打孔算法[5]和基于環路的符號級打孔算法[10]作比較，所有實驗數據均是在二進制輸入加性高斯白噪聲(BI-AWGN)信道下仿真獲得。譯碼端采用標準的LLR-BP譯碼算法，最大迭代次數為50。

圖6選用了碼長155的四元矩陣分別在BPSK、QPSK、8PSK三種調制方式下進行仿真，分別對10個、20個、30個變量節點進行打孔處理，相較于母碼碼率分別提高了0.03、0.06和0.1，即碼率為0.43、0.46和0.5。當誤碼率在10-2量級時，9組打孔對比差異不大，但到了10-4量級時，9組數據均獲得了0.2～0.4 dB的增益，可見本文算法在低階調制和高階調制下都能獲得一定程度的增益。

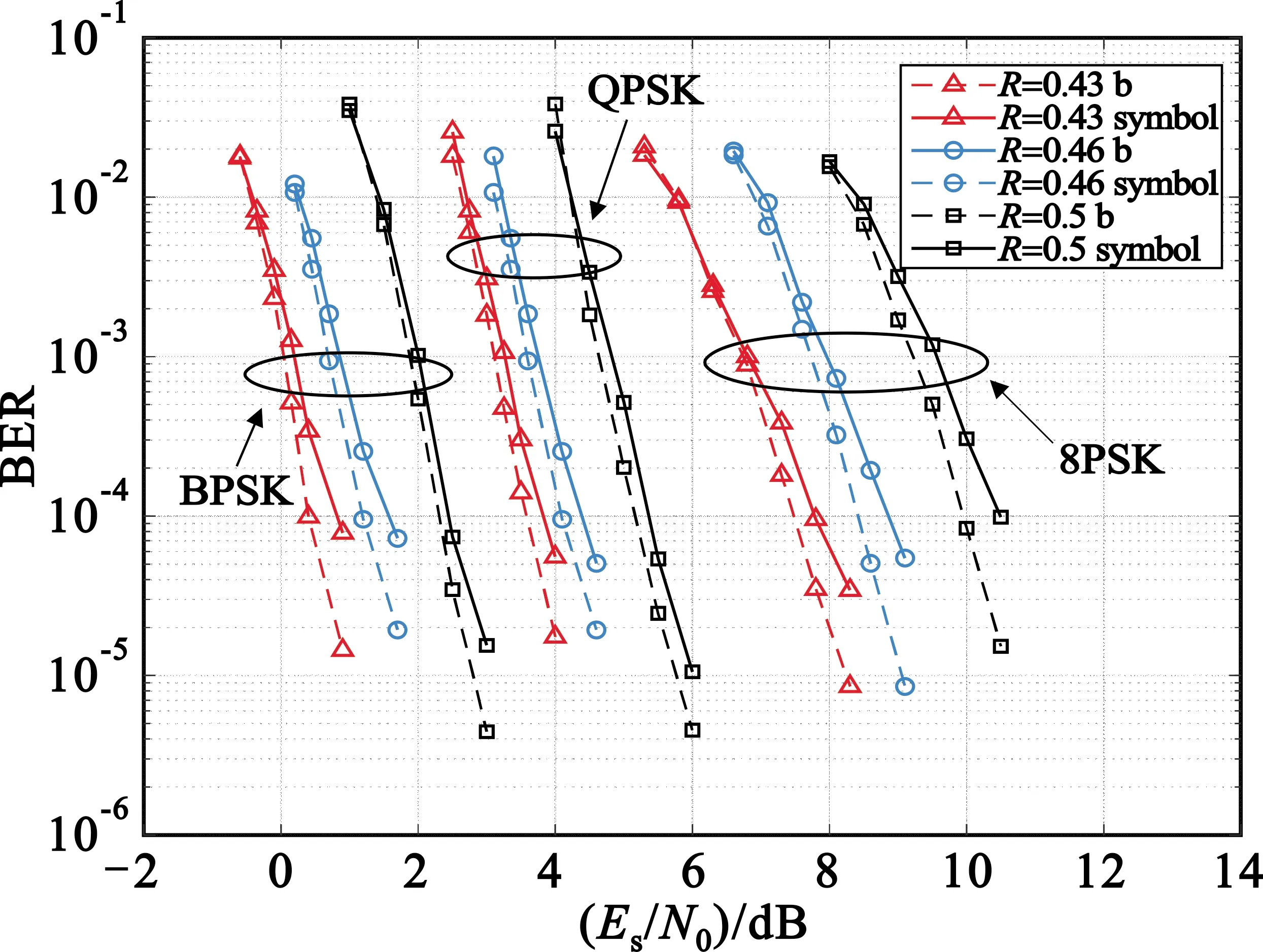
圖6 155碼長打孔對比圖

圖7給出了碼長576的四元矩陣在BPSK調制下的仿真結果，由圖可知碼率在0.6和0.7情況下，比特級新打孔算法的性能都優于傳統的符號級打孔算法，在10-3量級時兩種打孔算法信噪比分別增加了0.25 dB和0.2 dB，實現了碼率由低到高的轉變。

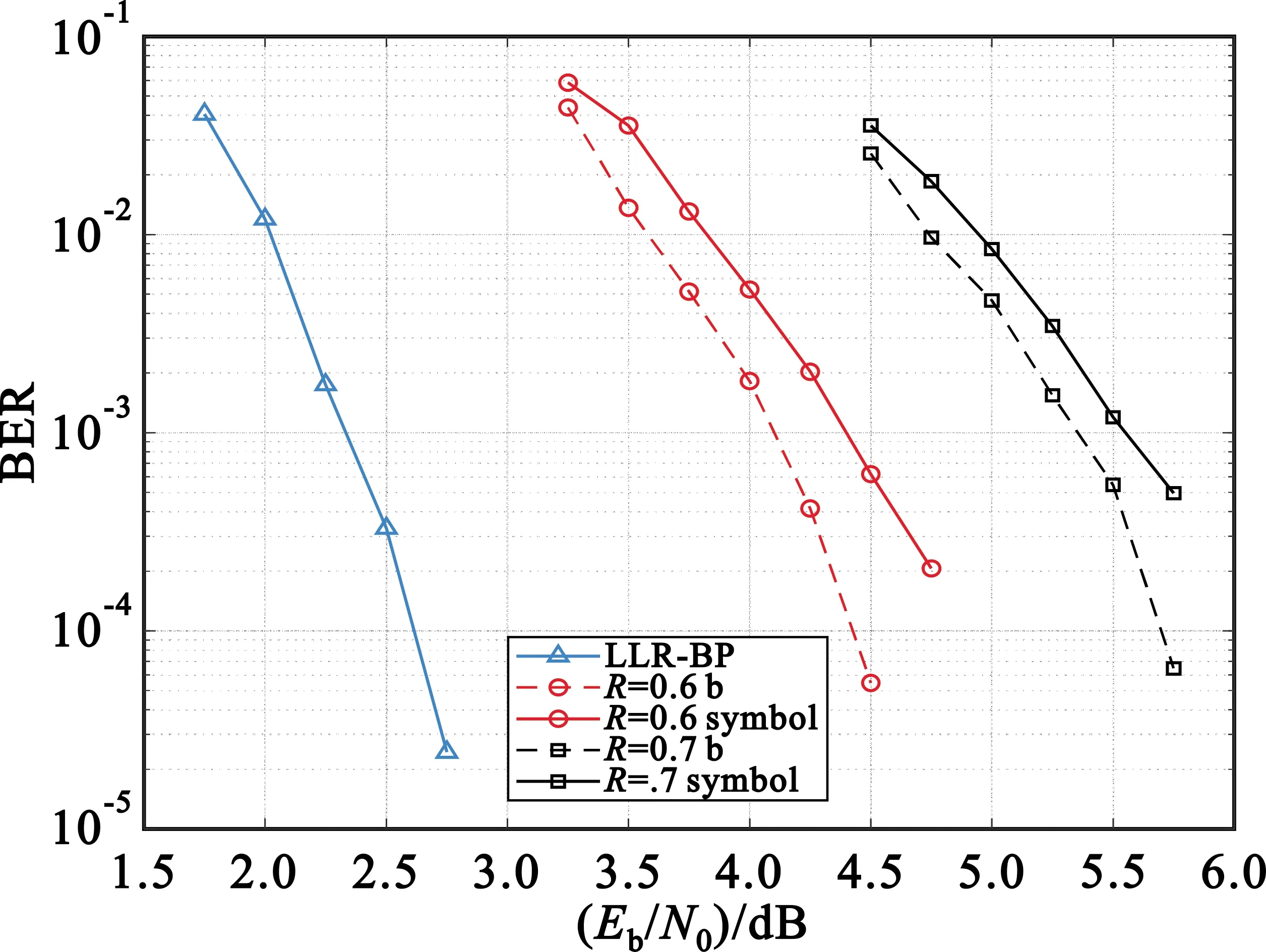
圖7 576碼長打孔對比圖

圖8給出了本文算法與文獻[10]中的基于環路的符號級打孔算法和傳統符號級打孔算法的對比，母碼碼率為0.5，采用BPSK調制，打孔后碼率都增加到0.6和0.7。兩組數據中在低信噪比區域時，比特級新打孔算法與基于環路的符號級打孔算法譯碼性能差異不大，幾乎持平，但隨著信噪比的增大，本文的新算法在10-4量級時擁有了0.2 dB的增益，性能良好。

圖8 比特級與符號級打孔對比圖

綜上所述，多元比特級新型打孔算法有比多元常規符號級打孔算法更佳的性能，在各碼率都獲得了一定的增益。

5 結束語

本文基于二進制鏡像理論提出了一種比特級的多元碼率兼容LDPC碼打孔算法，通過對多元矩陣進行二進制鏡像處理，再根據度分布選取合適的比特打孔節點，將打孔范圍從符號級擴展到比特級，實現了碼率由低到高的轉變。仿真結果表明，本文所提出的新型比特級打孔算法相較于傳統的符號級打孔算法，譯碼性能顯著提高，為通信系統中信息的傳輸提供了可靠性和有效性。比特級打孔節點的選擇不僅僅局限于度分布，未來研究可考慮恢復樹或環路對譯碼性能的影響。