基于MATLAB and Simulink的波浪能裝置液壓能量轉換系統仿真研究

葉 寅，盛松偉，樂婉貞，王坤林，張亞群

（1.中國科學院廣州能源研究所，廣東 廣州 510640；2.中國科學院可再生能源重點實驗室，廣東 廣州 510640；3.南方海洋科學與工程廣東省實驗室（廣州），廣東 廣州 511458；4.廣東省新能源和可再生能源研究開發與應用重點實驗室，廣東 廣州 510640）

波浪能作為一種可再生能源，具有儲量豐富、分布廣泛等特點[1]，并且在轉換過程幾乎不產生污染，因此受到越來越多的沿海國家重視，如何開發和利用波浪能成為了當前研究熱點。

波浪能最主要的利用方式就是發電，波浪能裝置一般通過三級能量轉換過程，將波浪能最終轉換為電能[2]。第一級是將波浪能轉換為機械能，第二級將機械能轉換為壓力能或其他形式的能量，第三級將壓力能轉換為電能。第一級能量轉換系統又稱為能量俘獲系統，二、三級轉換合在一起稱為能量轉換系統。根據能量轉換系統的不同可以將波浪能裝置分為氣動式、水力透平式、機械式和液壓式等[3]。由于波浪的方向和大小都是隨機的，且具有低頻、出力大等特性[4]，而帶有蓄能環節的液壓系統可以很好地緩沖由于波浪的這些特性帶來的沖擊，使最終的能量輸出平穩，達到并網的要求。因此液壓式的能量轉換系統成為當前波浪能裝置能量轉換方式的主流選擇，國際上比較著名的波浪能裝置如 Pelamis[5]、Wavestar[6]、Powerbouy[7]以及中國的“鷹式”系列波浪能裝置[8]都是選擇液壓轉換系統作為能量轉換方式。

目前，國內外對于波浪能裝置的研究主要集中在能量俘獲過程中裝置的水動力學部分，對于能量轉換部分的研究較少，在實海況下裝置的能量轉換系統的數據更為稀少。針對以上情況，本文對具有蓄能環節并且設有液壓自治控制器的波浪能能量轉換系統進行了仿真研究，同時利用實海況條件下的能量轉換系統試驗數據作為比對，驗證仿真模型的準確性。并模擬了在不同波浪條件下，液壓能量轉換系統的發電特性。本文的液壓式能量轉換系統仿真研究可以為實型波浪能裝置能量轉換系統的參數設計提供理論依據，為預測波浪能裝置發電功率提供參考。

1 液壓式能量轉換系統原理

波浪能裝置液壓發電原理如圖1所示。在波浪的作用下，吸波浮子隨波浪往復運動，連接在浮子上的液壓缸5做相同頻率的上下往復運動，液壓缸在往復運動的過程中，將液壓油從油箱12泵入到蓄能器組6中，當液壓缸往上運動，液壓缸有桿腔將液壓油經過單向閥2泵入蓄能器，液壓缸無桿腔通過單向閥3將液壓油吸入，當液壓缸往下運動時，無桿腔的液壓油通過單向閥4進入蓄能器組6。與此同時，有桿腔通過單向閥1從油箱12吸入液壓油。因此在液壓缸不斷的往復運動過程中，液壓油通過液壓缸不斷的被泵入蓄能器，蓄能器隨著液壓油的不斷增多，壓力逐漸上升，此過程將液壓缸的機械能轉變成了液壓油的壓力能存儲于蓄能器，實現了短期的能量蓄積。當蓄能器的壓力上升至設定值時，通過一定的邏輯控制方案，將液動換向閥9打開，蓄能器中的液壓油進行釋放，沖擊液壓馬達10，液壓馬達帶動發電機11旋轉，將液壓能轉換為電能。波浪比較小的情況下，由于液壓缸的運動速度比較慢，由液壓缸泵入蓄能器組的液壓油流量小于液壓馬達的流量時，蓄能器的壓力會下降，下降到設定的關閉壓力值時，通過控制液動閥，使液壓馬達和發電機停止旋轉，蓄能器組又開始下一個蓄能過程。如果波浪比較大，使液壓缸運動速度加快，由液壓缸進入蓄能器的流量大于液壓馬達的流量，進入蓄能器的液壓油多于流出的，蓄能器的壓力會繼續上升，直至相等，此時液壓馬達轉速基本穩定，系統連續發電。

為了實現上述控制方案，本文采用液壓自治控制器，如圖1中的元件8。液壓自制控制器主要由控制液壓缸13，蓄能器16，以及球閥14和15組成。液壓自治控制器的原理如下：當蓄能器組6的壓力增大時，控制液壓缸13左移，首先關閉球閥15（初始狀態是開啟），控制液壓缸13左腔的油逐漸進入蓄能器16，隨著蓄能器組6的壓力繼續增大，控制液壓缸13繼續左移，打開球閥14（初始狀態是關閉），此時控制油路可以通過14進入到液動換向閥閥9，液動換向閥9打開，液壓馬達開始工作；當蓄能器組6的壓力下降時，蓄能器16的液壓油會回到控制液壓缸13的左端，控制液壓缸13右移，關閉球閥14，液動換向閥9的控制油口仍有油，液動換向閥9仍處于打開狀態，隨著蓄能器組6的壓力繼續下降，控制液壓缸13繼續右移，直至打開球閥15，液動換向閥9控制油口的油通過球閥15流向油箱，液動換向閥9回復原位，液壓馬達關閉。

圖1 液壓能量轉換系統原理圖

2 系統數學模型

通過系統圖1可以看出，系統主要包括液壓缸、單向閥組、蓄能器、液壓自治控制器、馬達和發電機組。本文分別建立各個液壓元件的數學模型。

設液壓缸的運動速度為v，每次運動行程h，缸徑d1，液壓桿直徑d2，經過單向閥1吸油并通過單向閥2進入蓄能器的有桿腔流量Q1和經過單向閥3并通過單向閥4的無桿腔流量Q2分別表示為：

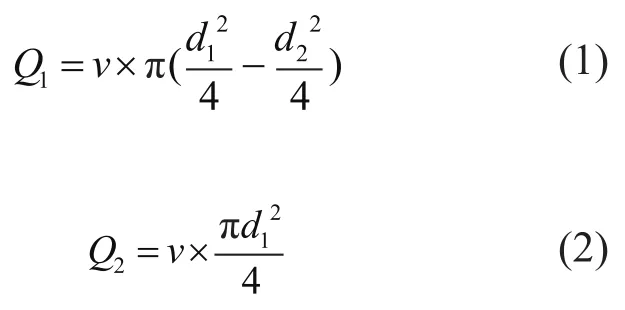
蓄能器采用皮囊式，如果蓄能器入口的流體壓力比皮囊內氣體的壓力高，則流體進入蓄能器并壓縮氣體，從而儲存能量。在整個發電過程中蓄能器經歷了兩個過程，一個是充油過程（氣體壓縮過程），一個是放油過程（氣體膨脹過程）。蓄能器皮囊內氣體的熱力學過程可以表示為:

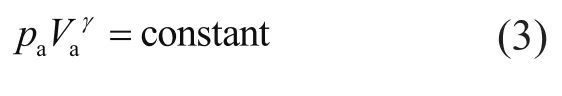
式中：pa為蓄能器壓力；Va為體積；γ為氣體常數。

設蓄能器的初始壓力為ppr，蓄能器的皮囊內氣體初始容積為Vpr，蓄能器中液壓油的容積VF和流量QF的表達式如下：

塑料件主壁厚的大小取決于產品需要承受的外力、是否作為其他零件的支撐、承接柱位的數量、伸出部份的多少以及選用的塑膠材料而定。從經濟角度來看，過厚的產品不但增加物料成本，同時也延長生產周期,增加生產成本。從產品設計角度來看，過厚的產品增加引致產生凹痕或氣孔等不良缺陷，大大削弱產品的剛性及強度。本研究主壁厚值分別采用：1.5、1.6、1.8、1.9、2.0、2.2、2.5、3.0 mm，其他條件保持不變，分析主壁厚變化對塑料件翹曲變形的影響。

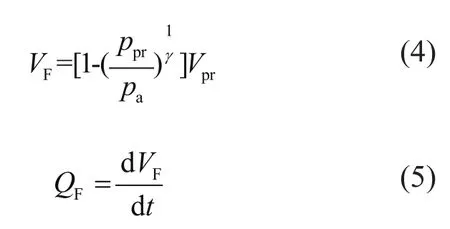
由液壓缸、蓄能器和馬達的連續性方程可得[9]：

式中：E為油液體積模量；Qm為馬達的流量。

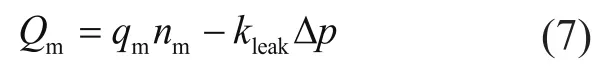
式中：qm為馬達排量；nm為馬達轉速；kleak為馬達泄露系數；Δp表示液壓馬達的進出口壓差，該值通過液壓自治控制器來控制，設定液壓自治控制器的開啟壓力為popen，關閉壓力為pclose。當蓄能器壓力pa＞popen，Δp=pa。當pclose＜pa＜popen時，會出現兩種情況，第一種是蓄能器處于充油過程（氣體壓縮過程），Δp=0；第二種是蓄能器處于放油過程（氣體膨脹過程），Δp=pa。馬達輸出轉矩Tm為：

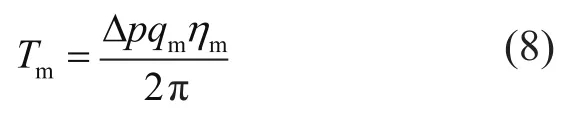
式中：ηm為液壓馬達機械效率。

液壓馬達和永磁發電機的轉矩平衡方程為：

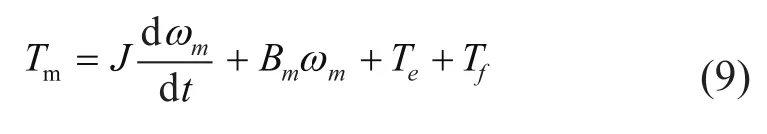
式中：J為馬達轉動慣量，單位kg·m2；ωm為馬達轉動角速度；Bm為馬達軸上的粘性阻尼系數；Tf為軸系靜摩擦力矩；Te為永磁同步發電機的轉矩。

三相永磁同步發電機，選擇三相正弦模型，假設電機鐵芯的導磁系數恒定不變，三相繞組完全對稱，永磁體產生的磁場沿氣隙周圍正弦分布。得到永磁同步發電機的電氣模型為[10]：

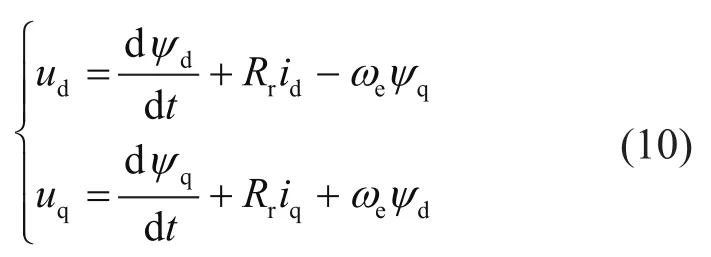
式中：ψd和ψq可以表示為：

式（10）～式（12）中：ud和uq分別為d軸和q軸的電壓；ψd和ψq以及ψf分別為d軸和q軸以及轉子的磁通量幅值；id和iq分別為d軸和q軸電流；Rr為發電機定子線圈繞組的電阻；ωe為發電機角速度。發電機的線電壓為：

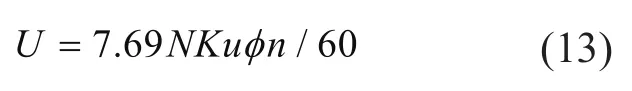
對于電阻負載模型，永磁同步發電機所接的負載為電阻負載，阻值為R，發電機功率可以表示為：

3 MATLAB and Simulink仿真模型

根據第2節中所建立的數學模型，利用MATLAB and Simulink軟件對波浪能裝置液壓轉換系統進行仿真實驗。首先建立系統的仿真框圖，根據系統的特點和MATLAB and Simulink液壓仿真軟件的特性，將液壓轉換系統分成3個子模型，分別是液壓子模型、控制子模型、發電子模型。液壓蓄能子模型包括液壓缸、單向閥組和蓄能器組和液壓馬達等，建立的仿真框圖如圖2所示。

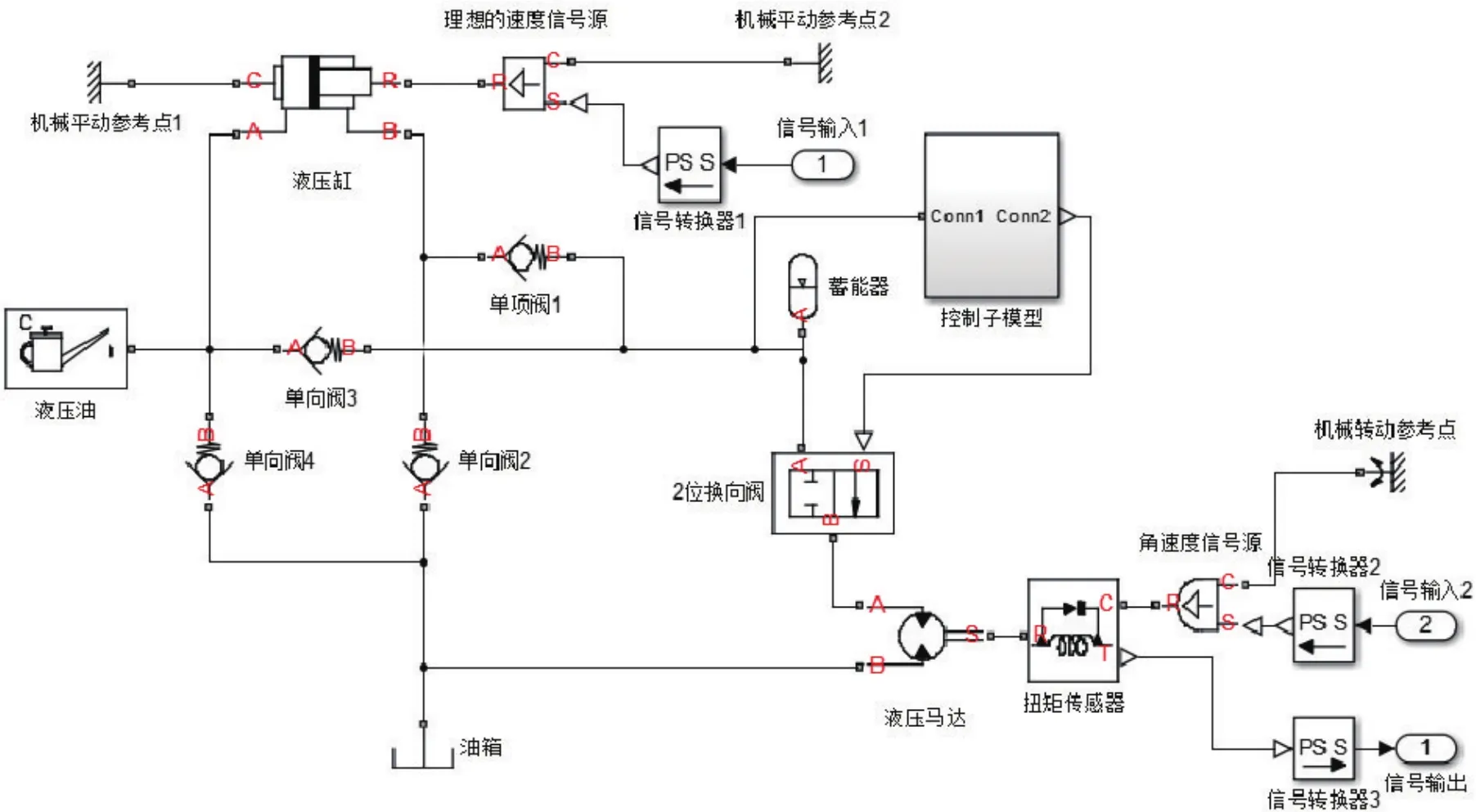
圖2 液壓子模型MATLAB and Simulink模型框圖

對于控制子模型，當蓄能器組壓力達到設定的開啟值時，主油路的液動閥打開，馬達開始發電，當蓄能器壓力降至設定的關閉值時，液動閥關閉，馬達也隨之關閉。控制系統都是由液壓元件組成，沒有電力電子元件，減少控制器在惡劣海洋環境下的故障，確保系統可以穩定的工作，這部分與其他采用液壓式轉換系統的波浪能裝置有所不同，控制子模型的MATLAB and Simulink框圖如圖3所示。

發電子模型包括永磁同步發電機和負載，MATLAB and Simulink模型如圖4所示。將建好的液壓、控制和發電子模型連接，得到能量轉換系統的模型框圖，設定仿真時間及相關參數，進行仿真。

圖3 控制子模型MATLAB and Simulink模型框圖

圖4 發電子模型MATLAB and Simulink模型框圖

4 實海況系統和仿真結果對比

為了驗證仿真的效果，將仿真數據和波浪能裝置實海況實驗所得數據進行比較。設置實驗參數如下，蓄能器容量為500 L，設置液壓自治控制器啟動壓力為16 MPa，關閉壓力為9 MPa，負載電阻為6 Ω，液壓馬達排量為107 mL/r，額定轉速1 500 r/min，發電機額定電壓400 V。仿真時液壓馬達容積效率取93%，總效率取90%[11]。

得到的實海況實驗結果和仿真結果如圖5至圖7所示。圖5是實驗得到和仿真得到的發電機功率曲線，兩條曲線基本重合，實海況實驗的發電平均功率為17.658 kW，仿真的平均功率為19.46 kW，二者之間的相對誤差為9.26%。圖6所顯示的是液壓馬達的流量曲線，實驗得到的平均流量為0.002 21 m3/s，仿真得到的平均流量為0.002 163 m3/s，實驗和仿真的相對誤差為2.12%。圖7所示的是發電機電壓的曲線，實驗所測的電壓平均值為320.69 V，仿真的電壓平均值為337.71 V，電壓的相對誤差為5.03%。

圖5 實驗和仿真得到的功率曲線

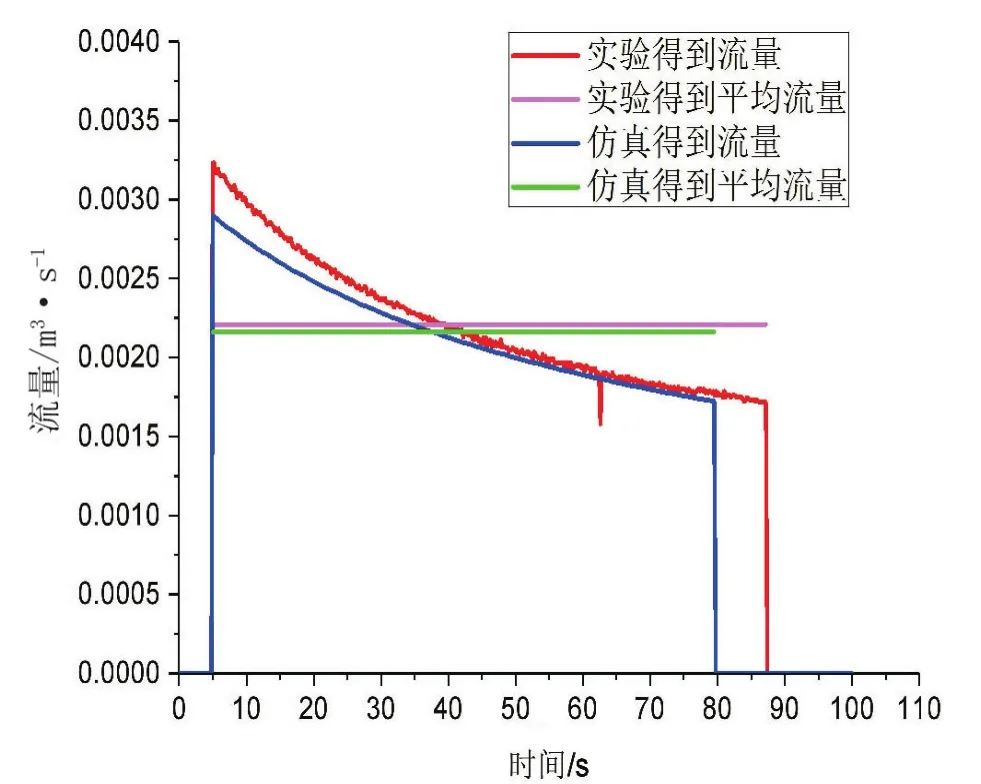
圖6 實驗和仿真得到的流量曲線

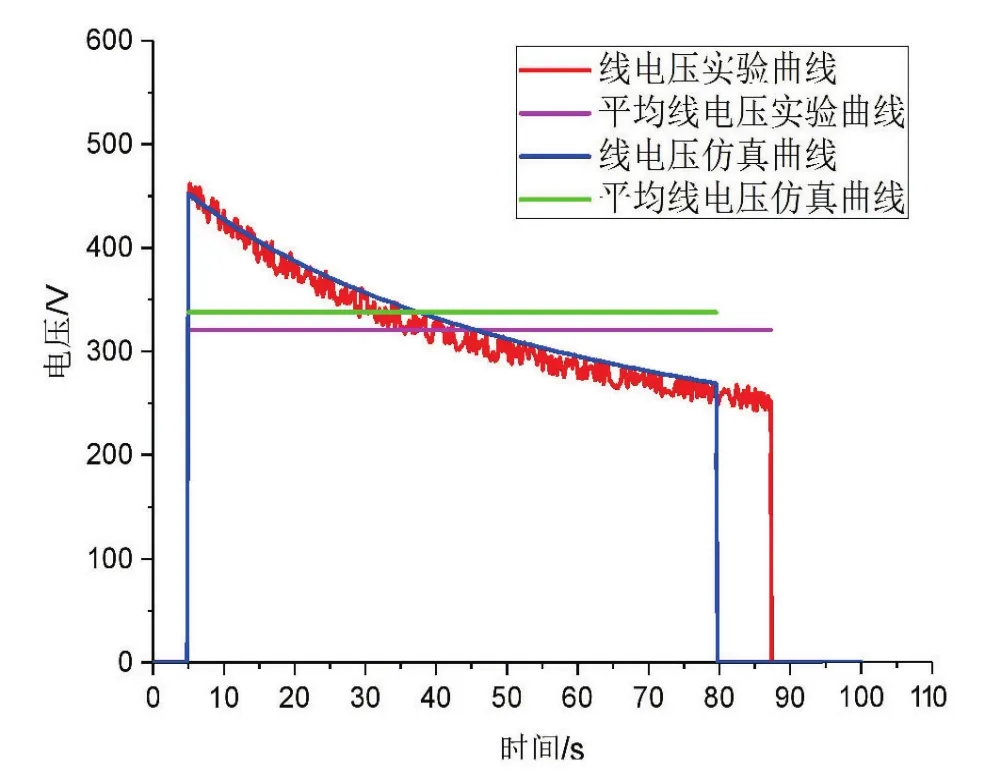
圖7 實驗和仿真得到的電壓曲線

通過得到的發電功率、液壓馬達流量以及蓄能器的壓力等數據，通過液壓發電端的效率公式（15）可以計算液壓系統的轉換效率。式中：Pi為錄得功率數據；Δt1,i為兩個功率數據之間時間步長；Q,i和pa,i分別為錄得的流量和功率數據；Δt1,2為錄得流量和壓力數據的時間步長。

通過計算得到，實型波浪能裝置液壓系統實驗液壓到電的效率為69.29%，模擬仿真得到的液壓到電的效率為76%。

5 規則波和隨機波下仿真及結果分析

為了研究不同波浪條件下液壓能量轉換系統的發電特性。本文分別做了隨機波和規則波下的能量轉換系統仿真。為了縮短仿真時間，修改了第4節的仿真參數，將蓄能器的容量改為100 L，液壓馬達排量改為65 mL/r，阻值改為8 Ω。給液壓缸端施加兩組不同的輸入信號來模擬波浪，一組是不規則的隨機速度信號，模擬不規則波浪，如圖8所示，另一組是規則的正弦信號，模擬規則波，如圖9所示。

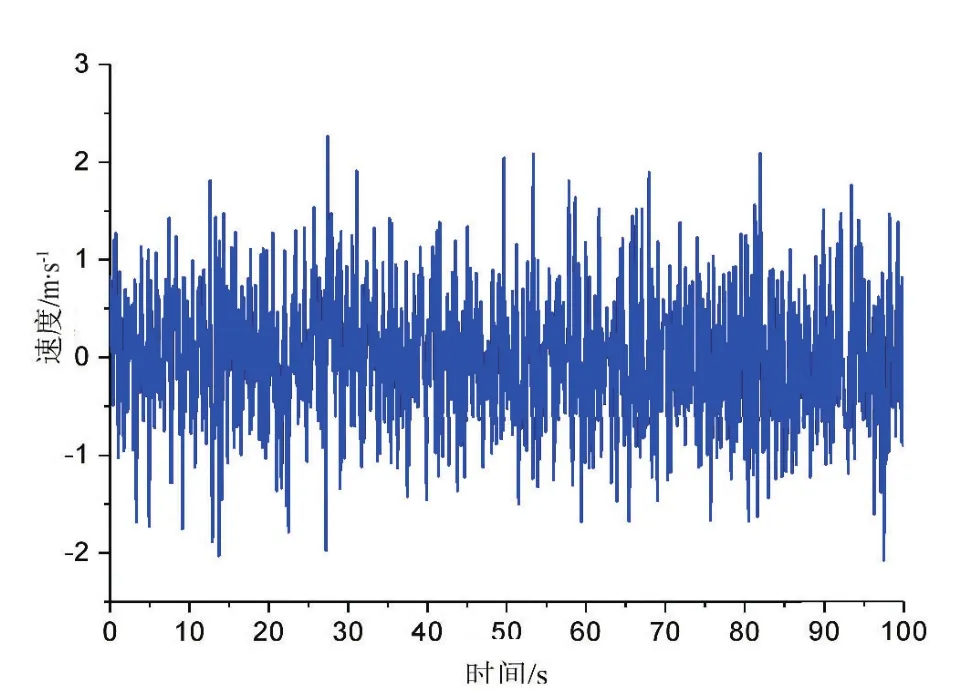
圖8 隨機速度信號

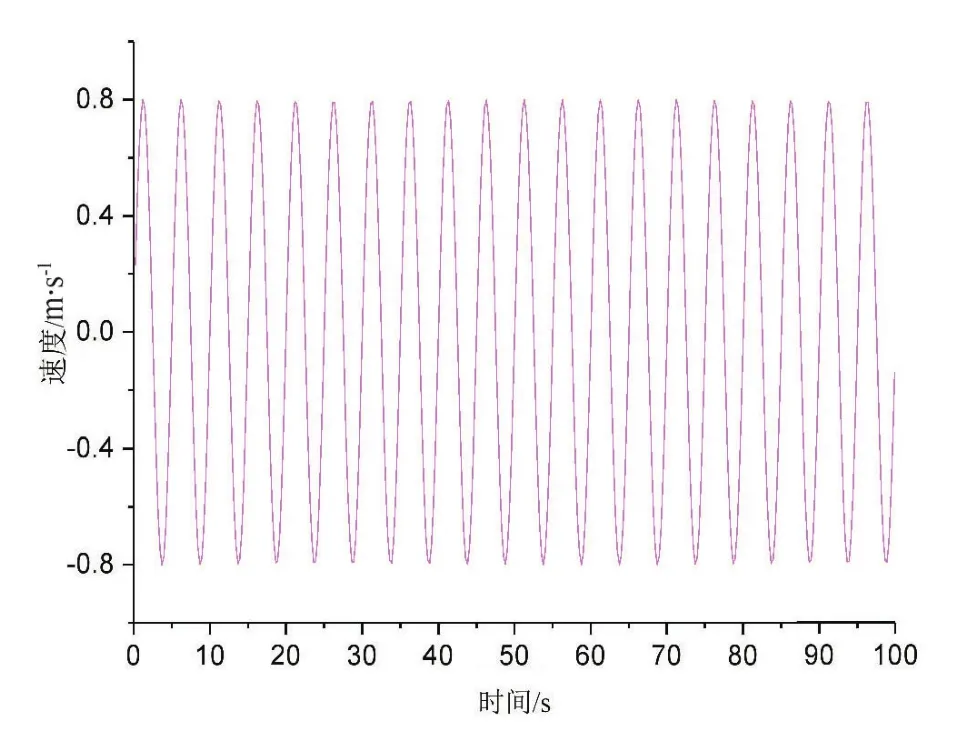
圖9 正弦速度信號

仿真時間為100 s，得到液壓缸有桿腔和無桿腔的流量如圖10和圖11所示，通過液壓缸的流量曲線可以看出，液壓缸的流量基本和輸入的信號相一致。

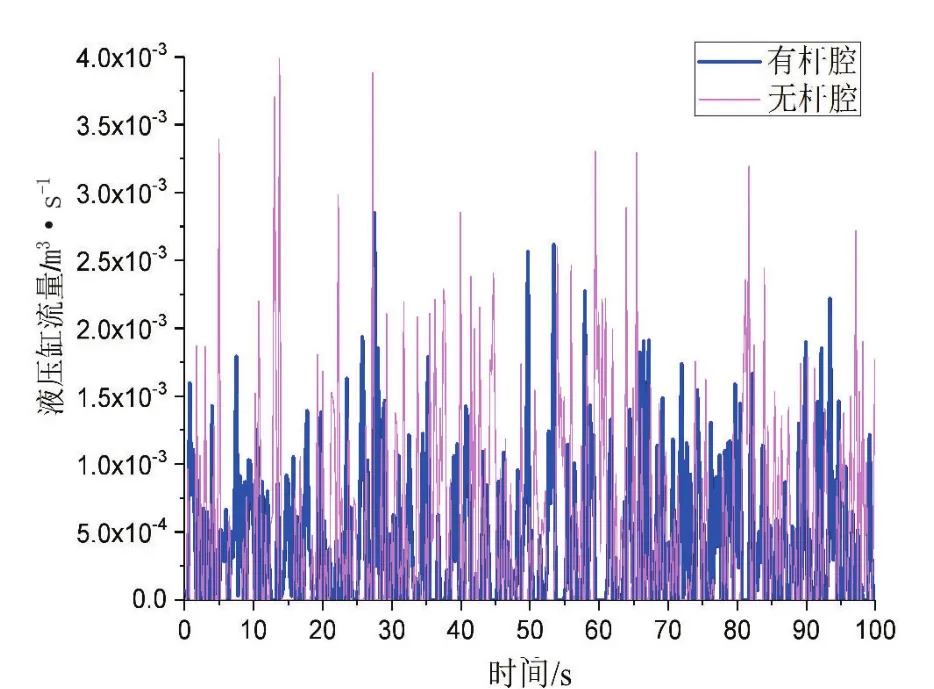
圖10 隨機信號下的液壓缸流量

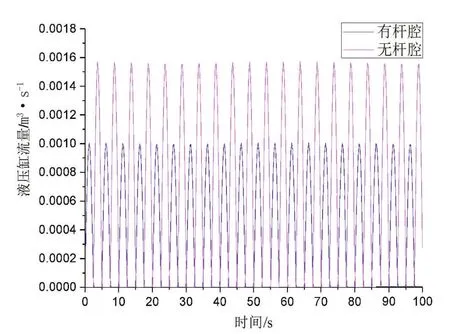
圖11 正弦信號下的液壓缸流量

圖12所示的是蓄能器中的壓力pa在兩種不同的輸入信號下的變化曲線，從圖12可以看出，經過蓄能穩壓之后，兩組工況下蓄能器的壓力值都在所設定的啟動壓力popen和關閉壓力pclose之間波動。

圖13至圖15所示的是兩組工況下發電特性曲線圖，分別為功率，轉速和電壓。從圖13得到，兩組信號下最大的發電功率值約為26.6 kW，最小發電功率為約為8.88k W，并且兩個工況下在系統進行發電時功率、馬達轉速和發電電壓曲線基本平行，曲線的趨勢和走向也基本一致，說明經過蓄能穩壓之后，系統的發電功率與輸入的信號已經基本沒有什么關聯性。

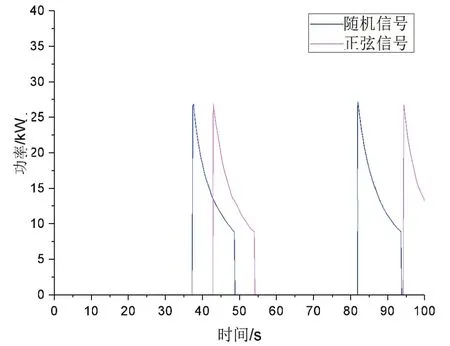
圖13 兩組工況下發電功率

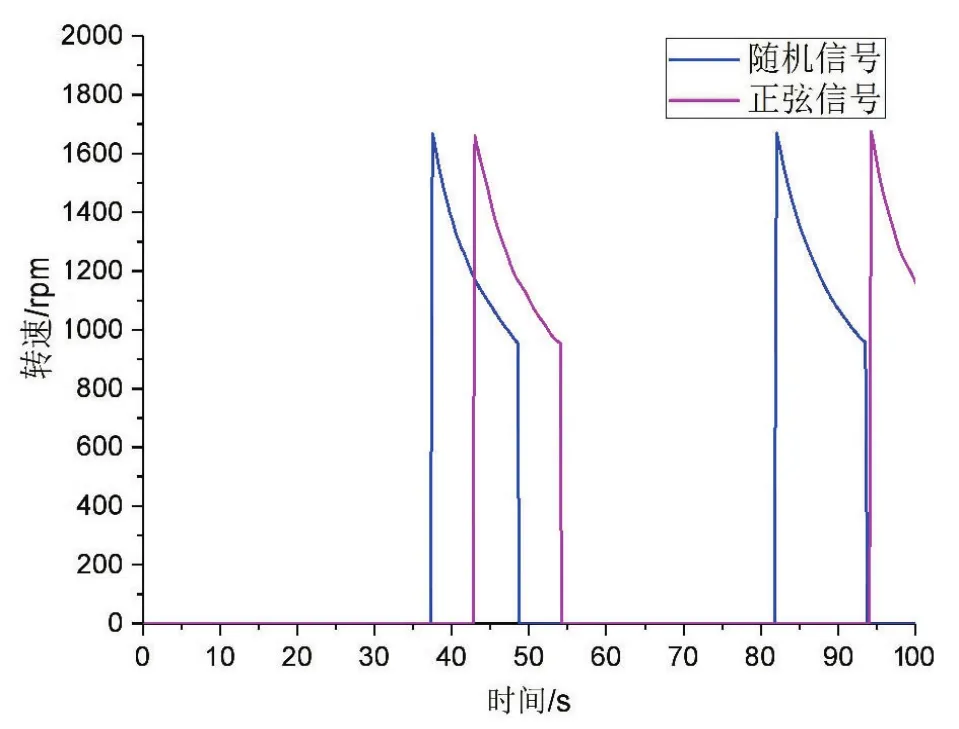
圖14 兩組工況下液壓馬達轉速

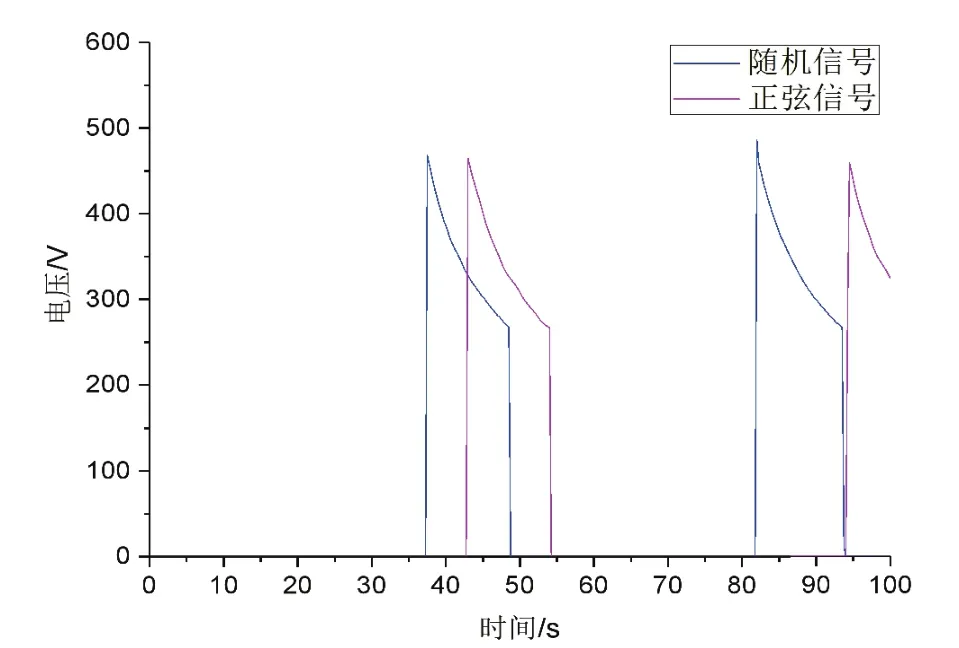
圖15 兩組工況下發電機電壓

6 結 論

本文研究了帶有蓄能環節和液壓自治控制器的波浪能裝置液壓能量轉換系統，通過對系統的建模仿真研究，得到以下研究結論：（1）將波浪能裝置實海況實驗與仿真結果對比，二者得到液壓能量轉換系統的發電特性（包括發電功率、液壓馬達的流量和發電機電壓）基本一致，實驗和仿真的相對誤差分別為9.26%、2.12%和5.03%。此外通過計算得到了實驗和仿真的液壓到電的效率分別為69.29%和76%，驗證了本文仿真模型的準確性；（2）通過模擬不同的波浪信號輸入，經過液壓能量轉換系統，在啟動壓力和關閉壓力設定的情況下，模擬隨機波和規則波輸入得到的發電特性基本相似，意味著通過本文所設計的液壓能量轉換系統，可以將不穩定的波浪能轉換成穩定的電能，最終輸出的電力特性曲線與輸入的波浪特性關聯性已經不大，輸出的功率和電壓比較穩定，提高了發電質量，從而使發電機后端的電力變換更為方便。