汲水斗對水面飛行器水動力性能的影響
王曉強,來曙光,肖志堅
1 海軍裝備部駐武漢地區第二軍事代表室,湖北 武漢 430064
2 中國艦船研究設計中心,湖北 武漢 430064
3 中國特種飛行器研究所,湖北 荊門 448035
4 高速水動力航空科技重點實驗室,湖北 荊門 448035
0 引 言
相比傳統消防手段,大型水面飛行器參與森林滅火具有多種優勢,例如機動性強、速度快、載水量大等[1]。目前,國內外學者經過多年的研究和實踐,已完成水面飛行器投汲水滅火系統的系列發展,并在實際應用中取得了顯著成效。在水面飛行器汲水裝置方面,目前國內外已公開的相關研究和文獻極少,主要集中在水面飛行器整體的氣?水動力性能方面。1959 年,Mottard[2]研究了水上飛機起飛過程中波浪對阻力的影響。2012 年,王永亮等[3]根據炸彈的連續計算投放點(CCRP)原理,獲得了投水算法的數學模型,最后結合自由紊動射流原理,提出了一種大型滅火飛機的投水算法。2015 年,黃淼等[4-5]對水陸兩棲飛機模型波浪試驗技術、飛機在波浪上的運動響應以及船體水動力矩特性進行了深入研究。2019 年,段旭鵬等[6]基于CFD 方法研究了水上飛機泊水時的空氣和水動力性能。
由于缺乏相關的研究,根據水面飛行器汲水斗的設計需要,本文擬開展如下研究:通過開展靜水拖曳試驗,研究汲水斗放下時不同汲水量下飛行器的阻力和姿態隨速度的變化規律;通過數值仿真分析,研究汲水斗的汲水效率、汲水載荷和附加俯仰力矩隨速度的變化規律,以及無、收起和放下汲水斗3 種條件下水面飛行器的阻力、升沉和縱傾等水動力特性的變化規律。
1 幾何模型與方法
1.1 幾何模型
以某水面飛行器無動力模型為試驗和仿真對象,開展靜水拖曳試驗(EFD)和仿真計算(CFD)。試驗和數值計算的工況如表1 所示。首先,開展汲水斗放下時3 種排水量(0.79Δa,0.85Δa和Δa)的水面飛行器靜水拖曳試驗;隨后,開展排水量為Δa時水面飛行器在無、收起和放下汲水斗條件下水動力性能的仿真計算。試驗模型和仿真對象如圖1 所示,無汲水斗、汲水斗收起和放下這3 種工況下的幾何示意圖如圖2 所示。
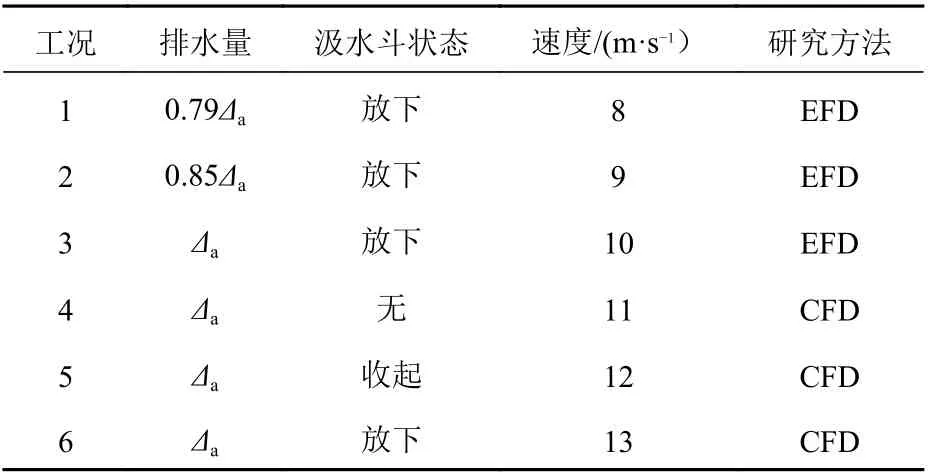
表1 試驗和數值計算的工況Table 1 Conditions of experiment and numerical simulation
圖1 模型的幾何特征Fig. 1 Features of the studied model
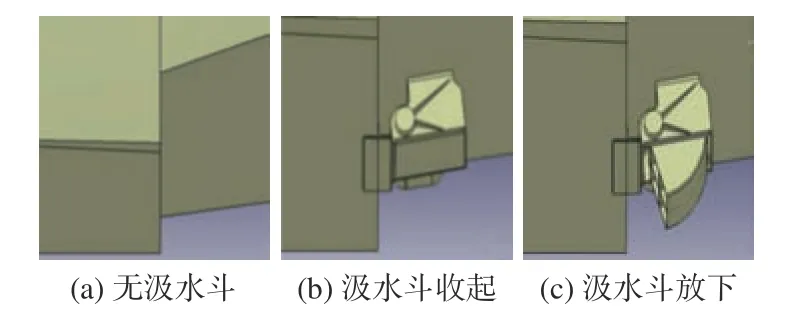
圖2 3 種工況下汲水斗狀態幾何示意圖Fig. 2 Features of bailer under three conditions
1.2 網格劃分
本文采用切割體網格生成高質量的壁面網格,通過體積控制的方法對復雜曲面或者流動分離嚴重的區域進行加密處理,例如自由液面、機身斷階吃水區域、各操縱面等。采用重疊網格解決飛機運動問題,同時,對重疊區域內的近壁面進行加密處理以精確捕捉近壁面流動。為保證空氣動力和水動力性能計算結果的準確性,分別考慮操縱面和船身邊界層的設置:各操縱面表面平均壁面y+值為1,邊界層層數15 層;機身表面平均壁面y+值為5,邊界層層數8 層。模型表面網格如圖3 所示。

圖3 模型網格分布Fig. 3 Mesh distributions of the model
網格計算域為:?1.0L≤x≤4.5L,?1.5L≤y≤1.5L,?1.0L≤z≤1.0L,其中x,y,z分別為計算域長度、寬度、高度方向的坐標值,L為水面飛行器的總長。由于模型幾何對稱,可采用一半模型進行仿真模擬,因此對稱面采用對稱面邊界條件,上游入口采用速度入口,下游出口采用壓力出口,上邊界、側邊和下邊界采用速度入口邊界條件;在模型表面定義無滑移的壁面邊界條件。計算域的邊界條件設置如圖4 所示。
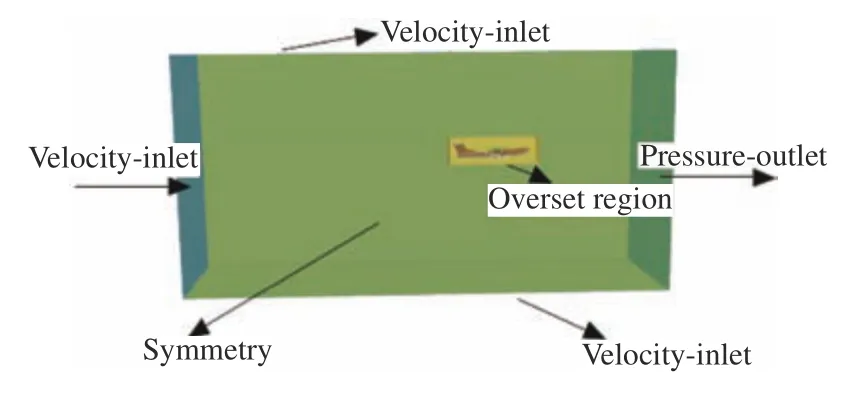
圖4 計算域邊界條件Fig. 4 The applied boundary conditions
采用RANS 方法求解,湍流模型采用SSTk-ω湍流模型[7]。采用二階迎風有限體積法(FVM)對控制方程進行離散化。對流項采用二階迎風格式離散,擴散項采用二階格式離散。自由液面捕捉采用兩相流體體積(VOF)技術。
2 拖曳試驗
2.1 試驗設計
真實的水面飛行器在汲水后會將汲取的水儲存在飛機特定的水箱中,而此次試驗中流經汲水斗的水通過汲水系統的管路從飛行器側面排出,根據需要,在拖車啟動之前,需將特定質量的水提前注入模型水箱。
試驗在拖車的前伸裝置上進行,如圖5 所示。圖5 所示模型的螺旋槳固定,不影響仿真與試驗結果分析對比。前伸裝置試驗裝置主要包括拖車、前伸裝置、運動裝置和限位裝置。其中,前伸裝置與拖車固結,用于將試驗模型的位置前伸至拖車前部;運動裝置是保證飛機自由度的安裝裝置,包括小滑車、升沉桿和重心連接桿,小滑車能在前伸裝置上沿航向在一定范圍內前、后移動,保證模型能沿航向自由平移,升沉桿穿過小滑車與重心連接桿上端固結,試驗時升沉桿隨模型垂向平移,以保證模型能自由升沉運動,重心連接桿下端在重心位置與模型鉸接,以保證模型能自由俯仰運動;限位裝置主要是對模型的偏航運動進行限制,避免模型試驗時出現偏航運動致使模型與池壁發生碰撞而發生危險,限位功能通過導航桿實現。

圖5 試驗裝置示意圖Fig. 5 Experimental layout
2.2 試驗數據
圖6~圖8 所示為工況1~3 的阻力和姿態試驗結果。由圖可知,隨著速度V的增大,各工況的無量綱總阻力系數(Ft/Δ)和無量綱升沉系數(Heave/L)增大,縱傾角減小;汲水量增大,其無量綱總阻力系數、縱傾角、無量綱升沉系數也增大。本文中升沉以上升為正,縱傾以艉傾為正。
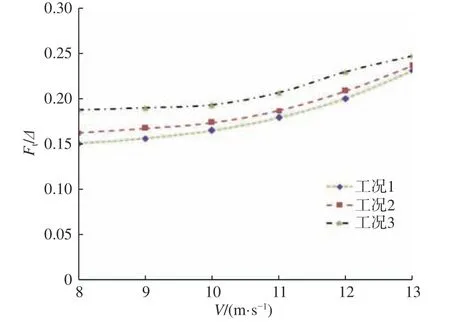
圖6 無量綱總阻力系數試驗結果Fig. 6 Experimental dimensionless total drag coefficient
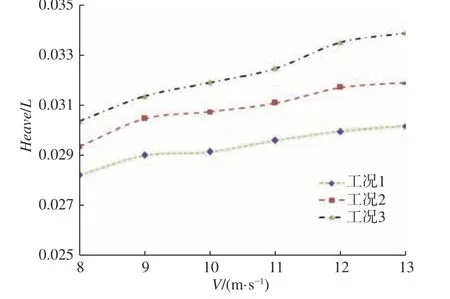
圖7 無量綱升沉系數試驗結果Fig. 7 Experimental dimensionless heave coefficient
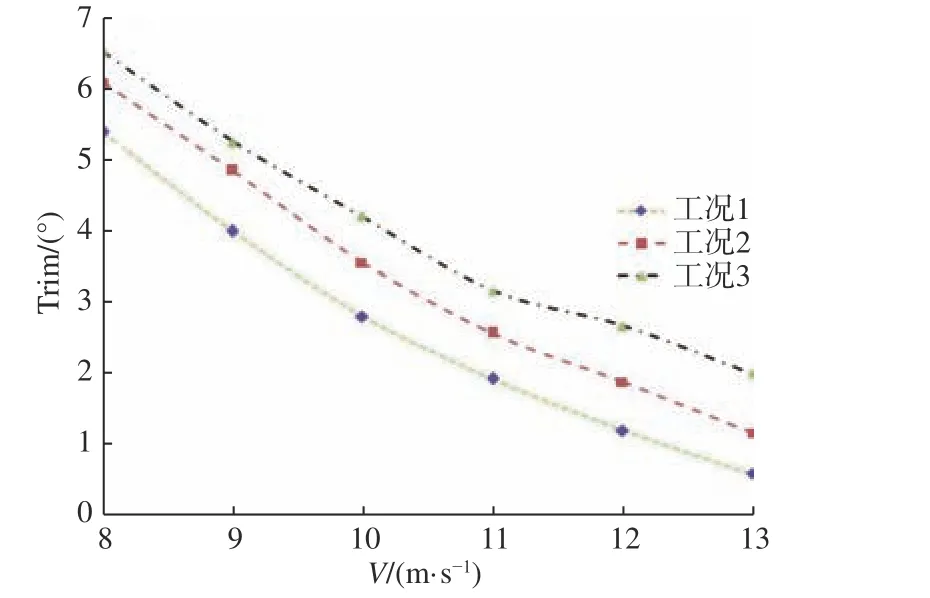
圖8 縱傾角試驗結果Fig. 8 Experimental trim angle
3 數值方法模擬
3.1 數值方法驗證
以工況3 和工況6 為例,通過對比汲水斗放下時水面飛行器模型的試驗和仿真計算結果,開展數值計算方法的驗證。幾何模型及網格劃分如第2 節所述。
如圖9 和圖10 所示,試驗中,不同速度下無量綱總阻力系數、無量綱升沉系數和縱傾角的趨勢與數值計算結果吻合較好,驗證了本文所采用計算方法的合理性和準確性。從圖9 中可看出,計算得到的水阻力均小于試驗值,這可能是因為相比物理試驗,數值計算中并沒有考慮池壁效應的影響,同時,軟件自身的自由液面捕捉模型無法完全模擬高速滑行時模型的噴濺阻力的原因。
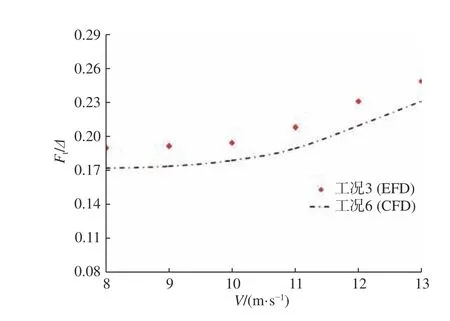
圖9 無量綱總阻力系數的試驗和仿真計算結果對比Fig. 9 Comparison of experimental and computed dimensionless total drag coefficient
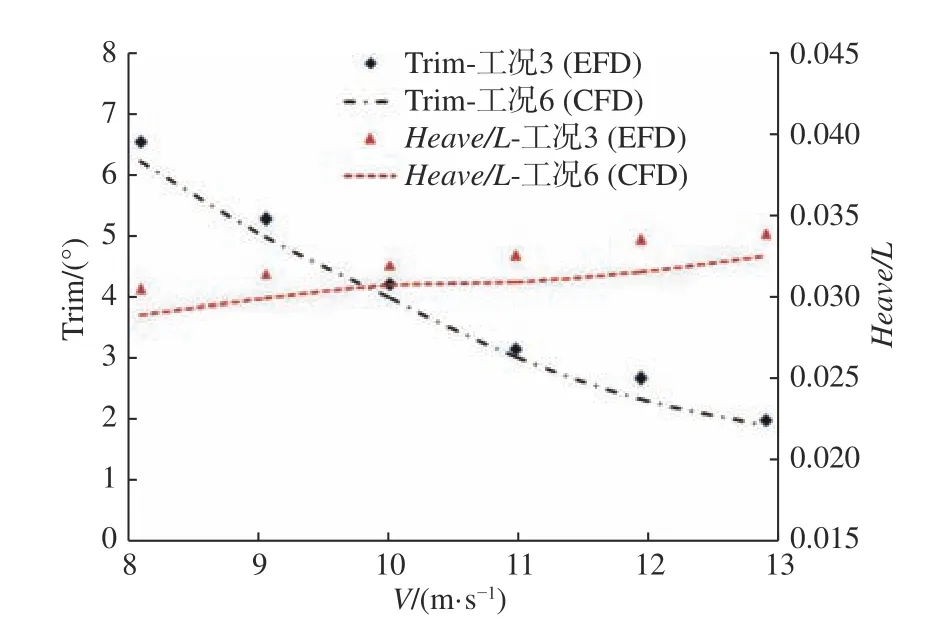
圖10 姿態的試驗和仿真計算結果對比Fig. 10 Comparison of experimental and computed attitudes
3.2 汲水斗的汲水效率和汲水載荷
由于需要在規定的時間內完成指定的汲水量,因此本文通過計算汲水斗的流量來分析汲水斗的汲水效率隨速度的變化規律。由圖11 可知,汲水斗的流量Q(單位:kg/s)是隨速度V(單位:m/s)的增大而增大的,且兩者呈非線性關系,因此采用二次多項式函數進行擬合,得到
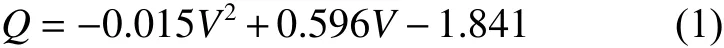
通過對比流量的計算值和擬合值,可以發現采用二次函數能很好地擬合汲水斗流量與速度之間的關系。不同速度下汲水斗入口的體積分數分布如圖12 所示。汲水斗浸水面積是隨著速度變化的,因此,汲水斗的汲水效率并不與速度成正比關系。
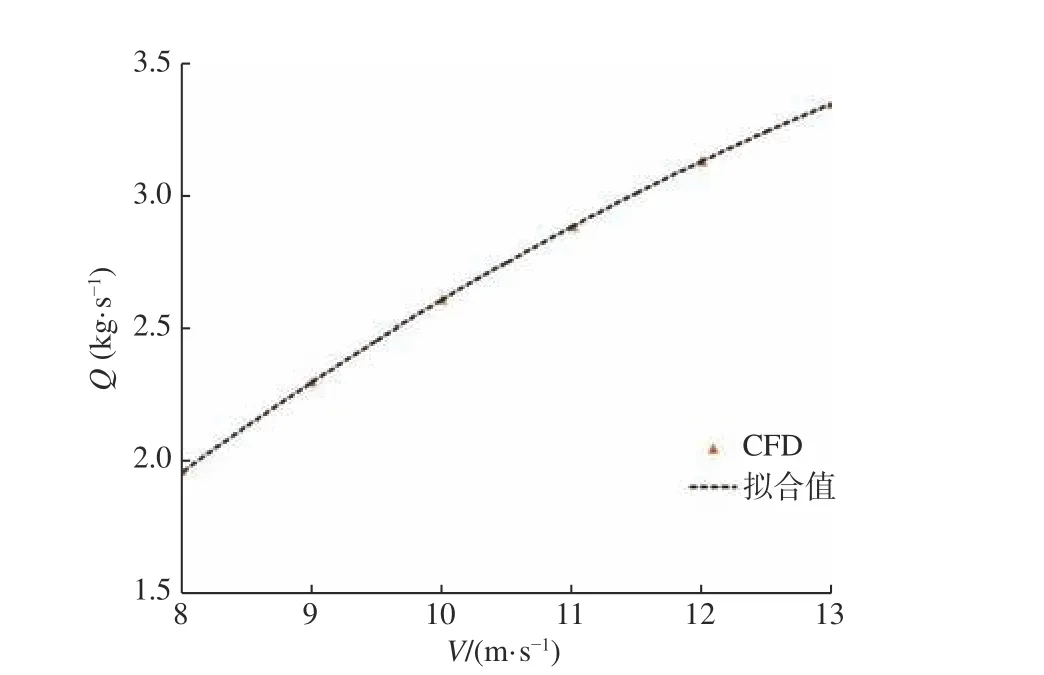
圖11 流量的計算值和擬合值對比Fig. 11 Comparison of computed mass flow and fitting value

圖12 汲水斗入口處的體積分數分布,8 m/s(a)和13 m/s(b)Fig. 12 Volume fraction of water at speed of 8 m/s (a) and 13 m/s (b)
在汲水過程中,在滿足汲水效率的同時,也需要關注汲水斗上的受載和產生的附加俯仰力矩,以免造成結構損壞和飛行器失控。以V=13 m/s為例,由圖13 可知,汲水斗放下時,汲水斗內部的壓力分布整體明顯大于汲水斗外部,汲水斗的受載可以分解為水平的阻力(Fx)和豎直向下(Fz)的拉力。圖14 表明,汲水斗收起時,升阻力系數均在0.002 以內,汲水斗的受力幾乎可忽略;而汲水斗放下時,阻力系數從0.02 增大至0.051,升力系數從0.018 增大到0.044,汲水斗受力明顯增大,且隨著速度的增大,Fx和Fz均呈非線性增長。圖15表明,汲水斗收起時,汲水斗產生的附加俯仰力矩系數在0.20 以內,幾乎可以忽略;而汲水斗放下時,汲水斗對機身產生的附加俯仰力矩系數隨著速度的增大,從1.59 增加至3.97,呈非線性增長。因此,在設計汲水斗時需要重點考慮汲水斗放下時汲水斗受力及產生的附加俯仰力矩。
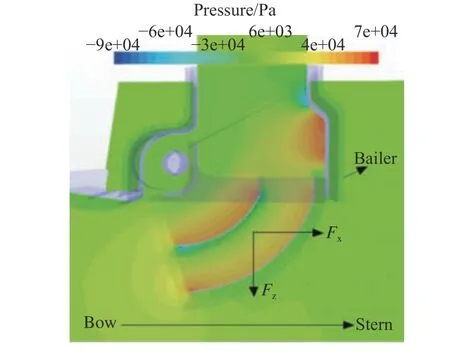
圖13 V=13 m/s 時汲水斗內、外部壓力分布Fig. 13 Pressure distribution of bailer at the speed of V=13 m/s
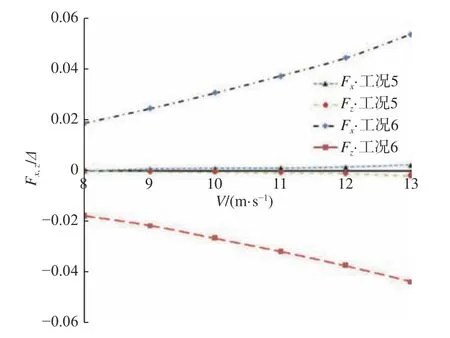
圖14 無量綱力系數計算值Fig. 14 Computed dimensionless force coefficients
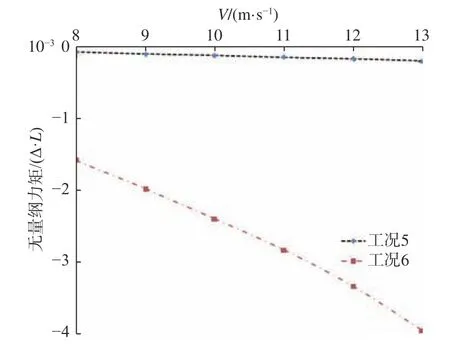
圖15 無量綱力矩系數計算值Fig. 15 Computed dimensionless moment coefficients
3.3 汲水斗對飛機總阻力的影響
圖16 所示為計算得到的3 種狀態下無量綱總阻力系數隨速度的變化曲線。由圖16 可以看出,無汲水斗和汲水斗收起這2 種情況下的總阻力較為接近,且隨著速度的增大均表現出先減小后增大的趨勢,變化幅度較小。相比之下,汲水斗放下時總阻力明顯增大,且隨速度近似呈二次曲線增長。圖17 所示為相對于無汲水斗情況,汲水斗收起和放下時引起的阻力增長率隨速度的變化情況。隨著速度的增大,同無汲水斗情況相比,汲水斗收起時的阻力增量較小,從2.6%增大到了6.0%,而汲水斗放下時的阻力增加較為明顯,是隨速度的增大而增大,從47.2% 增大到了95.7%。因此相對于無汲水斗情況,汲水斗收起時,對總阻力影響很小,而汲水斗放下時阻力急劇增加,且增幅隨速度的增大而增大。
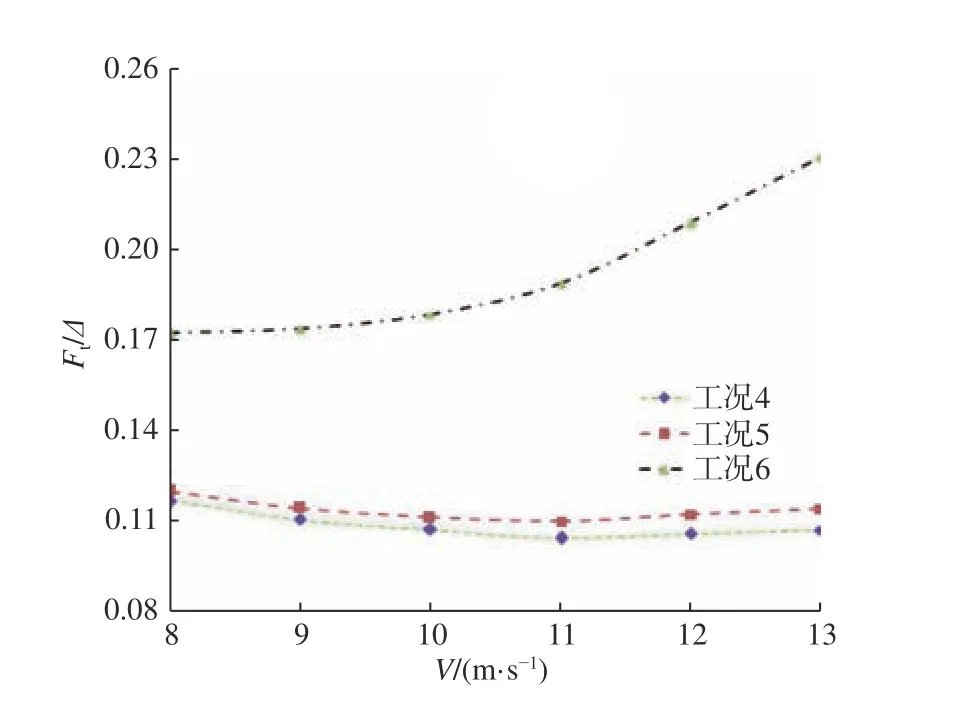
圖16 無量綱總阻力系數隨速度的變化規律Fig. 16 Variation of dimensionless total drag coefficient with respect to speed
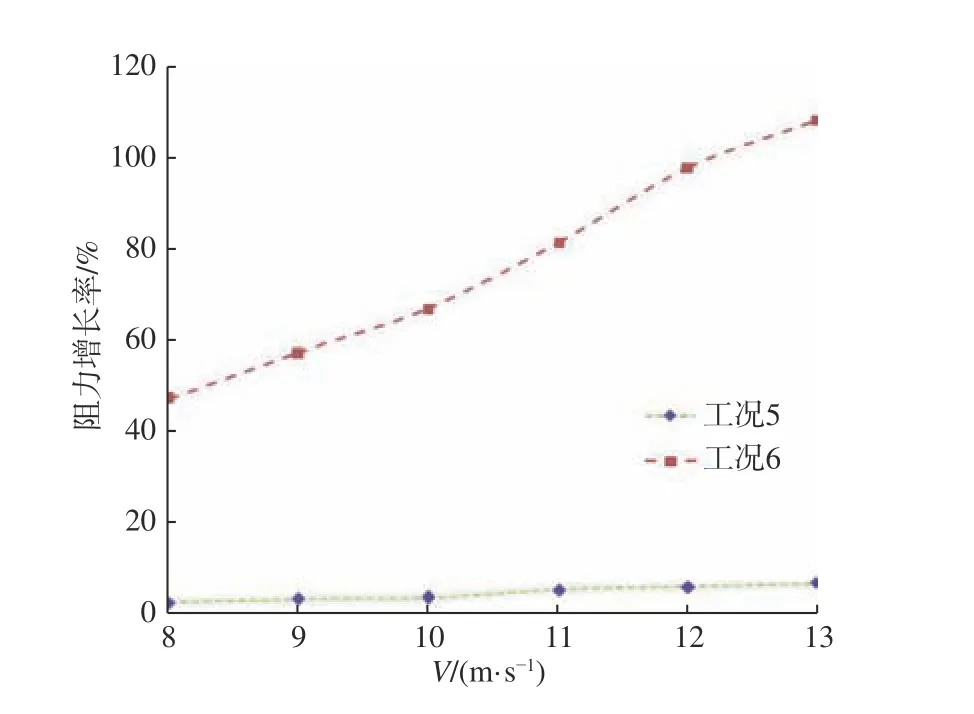
圖17 無量綱總阻力系數隨速度的變化規律Fig. 17 Variation of dimensionless total drag coefficient with respect to speed
3.4 汲水斗對滑行穩定性的影響
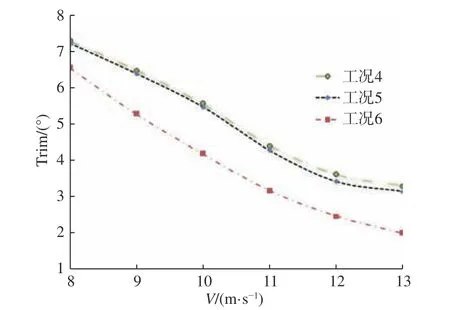
圖18 各工況縱傾角隨速度的變化規律Fig. 18 Variation of trim angle with respect to speed under different conditions
圖18 為3 種情況下機身縱傾角隨速度的變化曲線。由圖18 可以看出,隨著速度的增大,在3 種情況下機身的縱傾角均隨速度的增大而減小,相比無汲水斗情況,汲水斗收起時的機身縱傾角與其相差很小,而汲水斗放下時的縱傾角則明顯減小。由圖15 可知,汲水斗放下時,汲水斗產生了較大的附加俯仰力矩,抑制了機身的尾傾,因此汲水斗放下情況下的縱傾角幅值明顯減小;而汲水斗收起時產生的附加俯仰力矩非常小,可見汲水斗收起和無汲水斗時縱傾角幅值相差很小。圖19 所示為3 種情況下機身無量綱升沉系數隨速度增大的變化曲線。由圖19 可知,隨著速度的增大,3 種情況下機身的升沉幅值均隨速度的增大而減小了;汲水斗收起與無汲水斗時的縱傾角相差很小,而汲水斗放下時的縱傾角明顯大于其他2 種情況。雖然由圖14 可知,當汲水斗放下時,汲水斗受到向下的拉力,但是通過分析整個汲水系統(汲水斗加管路)的受力情況,整個汲水系統在所計算速度范圍內產生了2.3%~5.1%的升力,因此汲水斗放下時機身的上升幅度會大于其他2 種情況;而當汲水斗收起時,水流不經過汲水系統,且汲水斗處于機身斷階之后,垂向上受力極小,因此汲水斗收起時和無汲水斗時的升沉幅值相近。
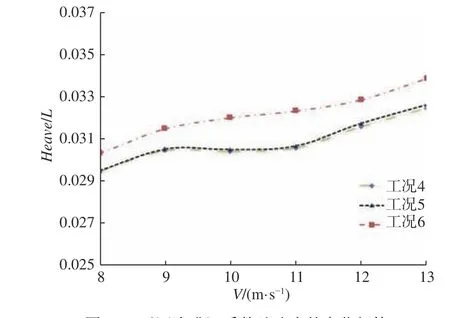
圖19 無因次升沉系數隨速度的變化規律Fig. 19 Variation of Heave/L with respect to speed at different conditions
圖20、圖21 所示分別為速度V=13 m/s 時汲水斗放下情況下自由液面分布的仿真計算結果與試驗結果。由圖20 所示的仿真計算結果來看,水面飛行器高速滑行時產生的凱爾文角較小,興波主要集中在后體區域,且可以觀察到斷階區域噴濺出的水浪貼近后體表面,具有吸附現象。興波波幅從飛行器船身斷階處開始增大至尾部開始衰減,水流從汲水系統的出水口噴射而出,隨即落入水面。由圖21所示的試驗結果也可以觀察到上述相似現象,從整體來說,試驗與仿真得到的自由液面的分布吻合較好。
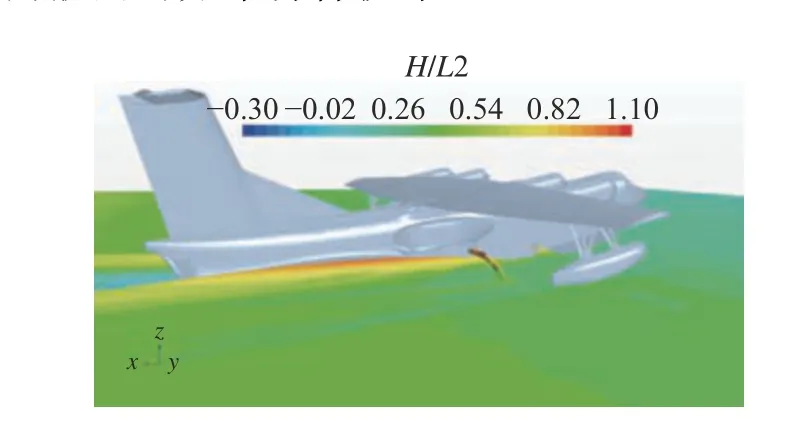
圖20 V=13 m/s 時仿真計算得到的自由液面分布Fig. 20 Computed free surface at speed of V=13 m/s

圖21 V=13 m/s 時試驗得到的自由液面分布Fig. 21 Experimental free surface at speed of V=13 m/s
4 結 論
本文通過開展試驗和數值計算,主要得到如下結論:
1) 試驗結果表明,隨著速度的增大,相同汲水量下的總阻力、升沉幅度均增大,縱傾角減小;汲水量增大時,總阻力、升沉幅度、縱傾角均增大。
2) 汲水斗的流量隨速度的增大而增大,且兩者呈非線性關系,采用二次函數可以很好地擬合汲水斗流量與速度之間的關系。汲水斗放下時,汲水斗上的阻力系數從0.02 增加到了0.051,升力系數從0.18 增加到了0.44,附加俯仰力矩系數從1.59 增加到了3.97,三者均隨著速度的增大而呈非線性增長。汲水斗收起時,其受力和力矩均可忽略。
3) 仿真計算結果表明,汲水斗放下時水面飛行器的總阻力明顯增大,且隨著速度的增大,相對于無汲水斗情況,總阻力增量從47.2%增大到了95.7%。與此同時,汲水斗放下后,水面飛行器的升沉將增大,縱傾角減小。汲水斗收起時,汲水斗對水面飛行器水動力性能的影響可以忽略。

