C30～C70井壁混凝土水化放熱效應及其溫度應力分析*

卞立波，孫志運，陶志，趙陽光

（1. 北京建筑大學，北京 100044；2. 河南省中陸工程技術(shù)有限公司，河南 鄭州 450000）

0 概述

對于礦井支護的井壁混凝土而言，厚度多大于1m，屬于典型的大體積混凝土。對大體積混凝土而言，體積大，膠凝材料水化引起的溫度變化給井壁混凝土的體積穩(wěn)定性帶來了不確定性。本文對 C30～C70 井壁混凝土的絕熱溫升性能進行了試驗研究，對其絕熱溫升進行數(shù)學計算，采用約束式溫度應力試驗機和約束系數(shù)法對 C30～C70 井壁混凝土的溫度—應力關系進行試驗研究和數(shù)值計算。探究了井壁大體積混凝土的溫度應力場的變化及分布規(guī)律，為評估井壁大體積混凝土的水化放熱效應提供參考依據(jù)。

1 試驗原材料及方法

1.1 試驗原材料

（1）水泥（C）：P·O42.5 水泥，技術(shù)指標見表1。

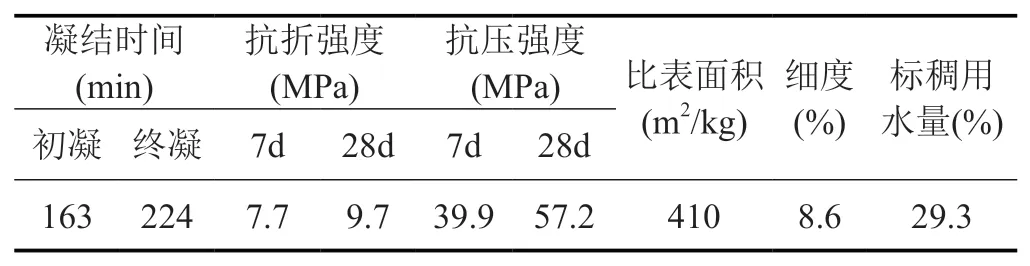
表 1 P.O42.5 水泥的技術(shù)指標

（2）粉煤灰（F）：Ⅱ級灰，基本性能見表 2。

表 2 粉煤灰的基本性能

（3）礦渣粉（S）：S95，基本性能見表 3。

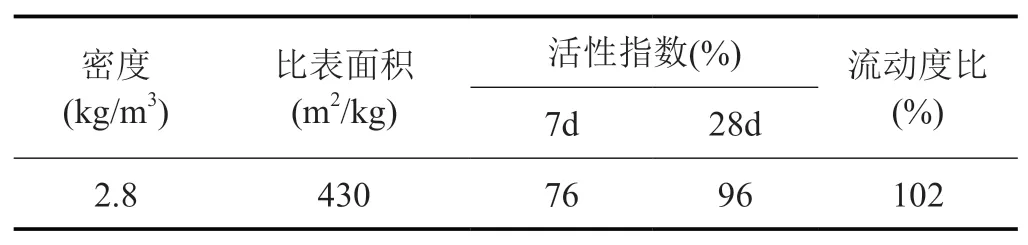
表 3 礦渣粉的基本性能

（4）石灰石粉（Lp）：密度 2.81g/cm3，比表面積470m2/kg，流動度比 105%。

（5）石膏：化學組成見表 4。

表 4 石膏的化學組成 %

（6）減水劑（A）：聚羧酸減水劑。

1.2 試驗方法

（1）膠凝材料水化熱測定

采用 Toni Technik Differential Calorimeter Model 7338 水化熱測試儀，膠凝材料 10g，水膠比為 0.5，水化溫度為 25℃，測試時間 72h。

（2）混凝土絕熱溫升測定

參照 DL/T 5150—2017《水工混凝土試驗規(guī)程》中混凝土絕熱溫升測試方法，溫度范圍 10～85℃，對中心試件完成固定齡期的溫度監(jiān)測，獲得井壁混凝土的溫升峰值和溫升速率。

（3）混凝土溫度應力測定

采用約束式溫度—應力試驗機測試井壁混凝土的溫度應力。

2 試驗配合比

采用國內(nèi)某礦井施工實際配合比，見表 5。

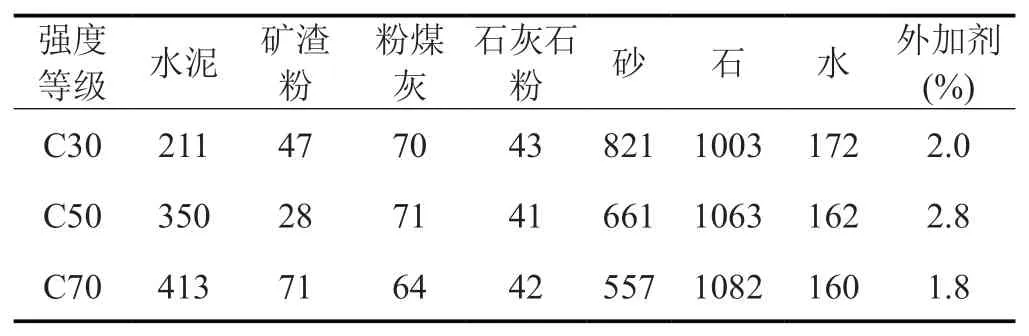
表 5 配合比 kg/m3

3 試驗結(jié)果及分析

3.1 膠凝材料的水化熱試驗結(jié)果

C30～C70 井壁混凝土的膠凝材料 72h 水化放熱量和放熱速率見表 6。

表 6 膠凝材料水化熱試驗結(jié)果

3.2 膠凝材料水化熱數(shù)值計算

基準水泥是由 C3S、C2S、C3A、C4AF、CaSO4以及游離氧化物構(gòu)成，其礦物組成的水化熱疊加則為水化熱，其水化熱可通過以下公式來估算[1-2]：

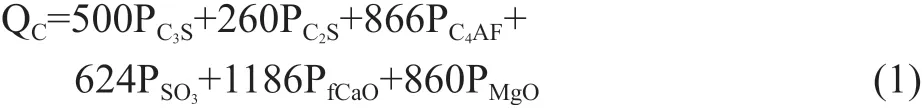
式中：QC——理論上水泥所有組份完全水化時的總水化熱，J/g。

本文采用基準水泥的礦物構(gòu)成見表 7。

表 7 基準水泥的礦物組成 %

摻加礦物摻合料的膠凝材料在完全水化情況下，最終水化熱可用下式表示：

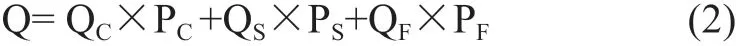
式中：

Q——100% 水化時膠凝材料的總水化熱，J/g；

QS、QF——分別為高爐礦渣和粉煤灰的水化熱，

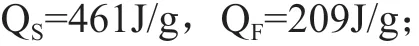
PC、PS、PF——為膠凝材料中水泥、高爐礦渣、粉煤灰的質(zhì)量分數(shù)，%。

對膠凝材料的水化放熱量計算，理論計算值與實測值見表 8。

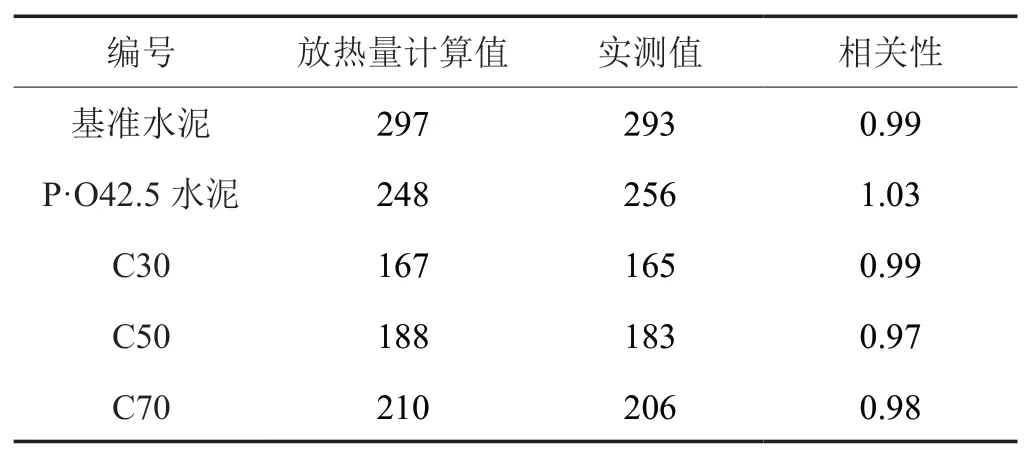
表 8 膠凝材料水化放熱量計算值 J/g

3.3 井壁混凝土絕熱溫升試驗研究

井壁混凝土厚度基本都大于 1m，大體積混凝土的溫升問題在井壁混凝土中同樣存在。混凝土的絕熱溫升可以評價混凝土的溫升情況[3]，絕熱溫升值和溫升速率又反映了早齡期混凝土的水化速率和水化程度。絕熱溫升試驗結(jié)果見圖 3。

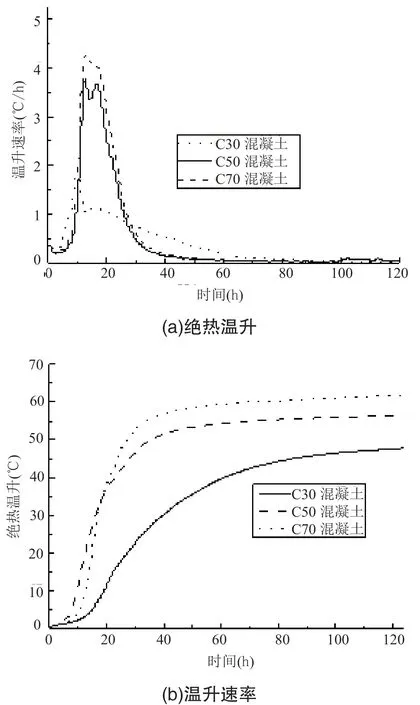
圖 2 混凝土絕熱溫升曲線

由圖 2 可得，C30 水泥混凝土 120h 的絕熱溫升為48℃，最大溫升速率為 2.22℃/h，溫升速率最快時間體現(xiàn)在 20～60h 之間，即混凝土澆筑完成的 1～3d 之間。C50 混凝土 120h 的絕熱溫升為 57℃，最大溫升速率 4.7℃/h。溫升速率最快時間出現(xiàn)在從澆筑開始到40h 之間，即澆筑完成 2d 之內(nèi)，就 C50 混凝土而言，溫升曲線與 C30 基本一致。C70 混凝土 120h 的絕熱溫升為 62℃，最大溫升速率為 12℃/h，絕熱溫升速率最快出現(xiàn)在從澆筑開始到 35h，即澆筑完成一天半之內(nèi)。C30～C70 混凝土溫升放熱曲線基本一致[4]。

3.4 混凝土絕熱溫升數(shù)值計算

現(xiàn)有對于混凝土的絕熱溫升計算方法仍然是基于普通混凝土配合比的基礎上，通過對水泥的水化放熱進行計算，然后推算混凝土的絕熱溫升，未考慮到現(xiàn)代混凝土技術(shù)中膠凝材料的變化，尤其是對于井壁混凝土而言。

在基于膠凝材料變化水化放熱的基礎上，對傳統(tǒng)絕熱條件下的溫升計算方法進行改進，絕熱條件下的溫升可用式 (3)、(4) 計算[5-7]：

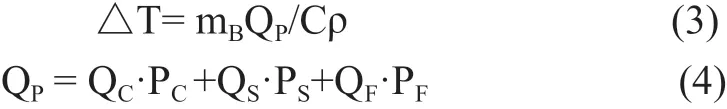
式中：

Qp——總放熱量，J/g；

mB——膠凝材料量，g；

ρ——混凝土的密度，g/cm3；

C——混凝土的比熱容，J/(g·℃)。

井壁混凝土的比熱容可用式 (5)、(6) 計算：

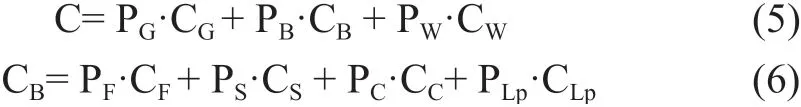
式中：

CG、CW、CF、CC、CS、CLp——分別為砂石、水、粉煤灰、水泥、礦渣粉和石灰石粉的比熱容，J/(g·℃)；具體數(shù)據(jù)見表 9。

PG、PB、PW——分別為骨料、膠凝材料和水所占比例，%。

表 9 常見材料的比熱容 J/(g·℃)

計算得 C30～C70 井壁混凝土的比熱容見表 10。

表 10 井壁混凝土比熱容 J/(g·℃)

參照膠凝材料水化熱，計算 C30～C70 井壁混凝土的絕熱溫升值，見表 11。改進后絕熱溫升計算方法計算所得溫升值與試驗所得溫升值相差不大[4]。

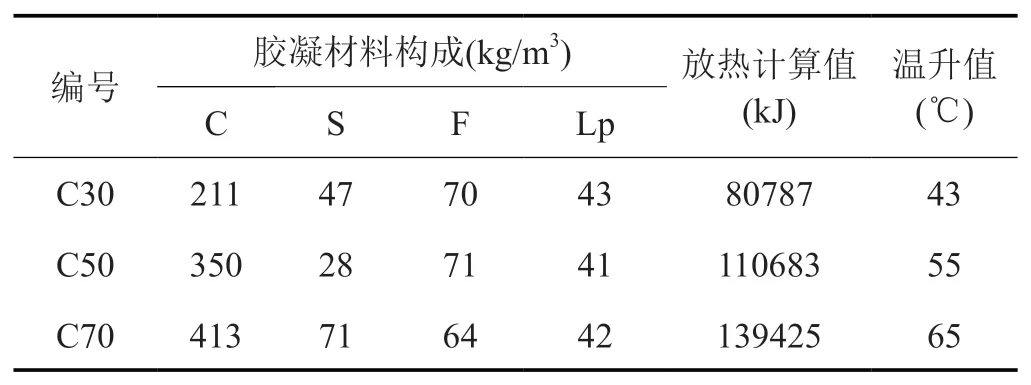
表 11 C30～C70 井壁混凝土計算溫升值

3.5 井壁混凝土溫度—應力關系的試驗研究

C30、C50、C70 井壁混凝土的溫度應力試驗結(jié)果如圖 3。

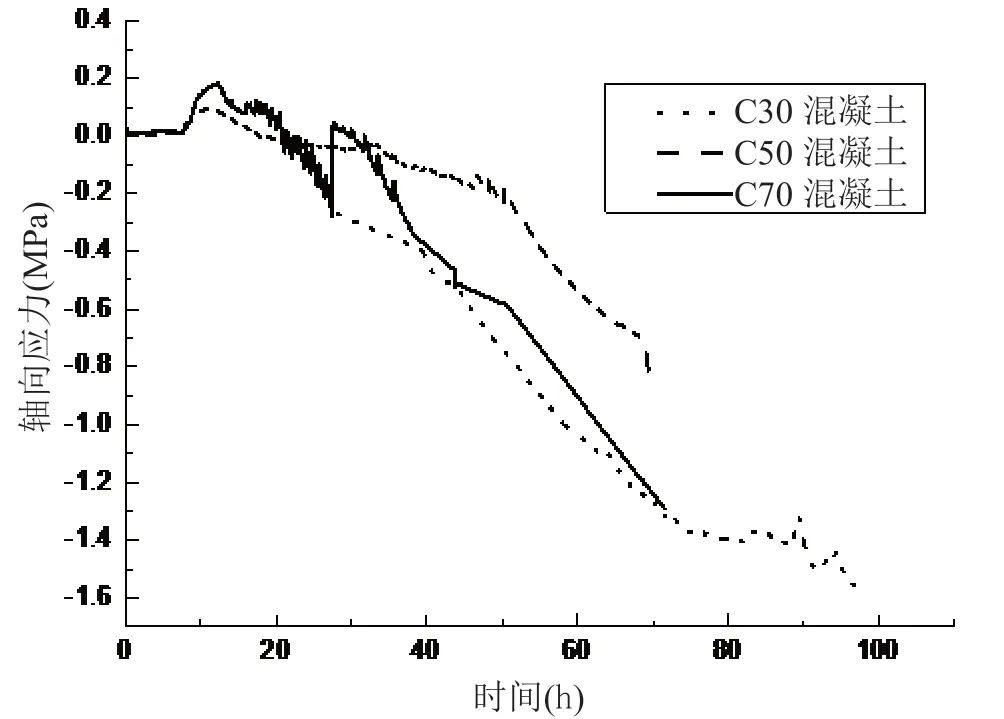
圖 3 溫度應力示意圖

由圖 3 可以看出，C30 井壁混凝土從澆筑開始，溫度從 18℃ 到 36℃ 又降低至室溫，開裂所產(chǎn)生的溫度應力為 0.9MPa。C50 井壁混凝土的從澆筑開始，其溫度從 17℃ 到 38℃ 又降低至室溫，開裂產(chǎn)生的溫度應力為 1.45MPa。C70 井壁混凝土從澆筑開始，溫度從18℃ 到 50℃ 又降低至室溫，開裂所產(chǎn)生的溫度應力為1.6MPa[4]。

混凝土的徐變會顯著降低混凝土內(nèi)部溫度應力。最初 12h 內(nèi)混凝土彈性模量發(fā)展較快，混凝土獲得了較大的預壓應力，此階段水化放熱相對較小，隨齡期的增長，混凝土的強度開始上升，放熱量增大，此時混凝土受到自身收縮的影響，預壓應力在有條件約束的情況下變?yōu)槔瓚Γ瓚Φ某掷m(xù)增長使混凝土受到的拉力也逐漸增大，當其所承受拉應力大于其抗拉極限條件后，混凝土開始開裂。混凝土開裂評價指標用“開裂敏感系數(shù)”表示，計算公式見式 (7)、(8)。井壁混凝土開裂敏感系數(shù)見表 12。

式中：

μ——開裂敏感系數(shù)；

k——防開裂安全系數(shù)；

P——混凝土的溫度應力，MPa；

ft——實測混凝土的抗拉強度，MPa。

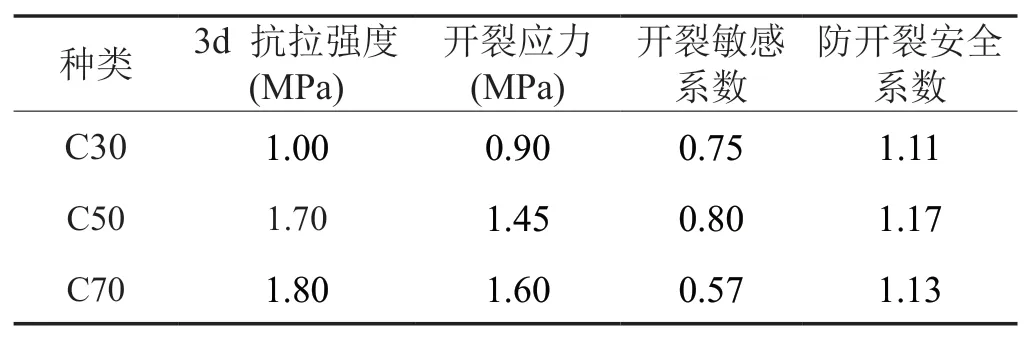
表 12 井壁混凝土開裂敏感性系數(shù)

3.6 井壁混凝土溫度—應力數(shù)值計算

目前對于溫度—應力的計算模擬也多采用約束系數(shù)法[6,8,9]。其計算式如式 (9)。

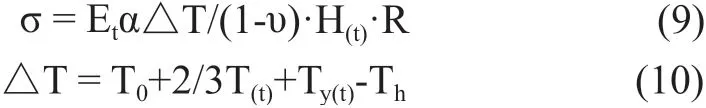
式中：

△T——溫升，℃。

T0——混凝土的入模溫度，取 18℃；

T(t)——混凝土水化絕熱溫升值，采用基于膠凝材料放熱量計算的絕熱溫升值，見表 13。

Ty(t)——混凝土收縮當量溫差，℃；

εy(t)——t 齡期條件的混凝土收縮變形值，采用混凝土的接觸式收縮變形值。

表 13 C30～C70 井壁混凝土 3d 收縮當量溫差

Th——混凝土穩(wěn)定后的溫度，℃，取 20℃。

Et——t 齡期的混凝土彈性模量；

α——混凝土的線性膨脹系數(shù)，1.0×10-5；

R——混凝土的外約束系數(shù)，一般地基取 0.25～0.5，本次取 0.5。

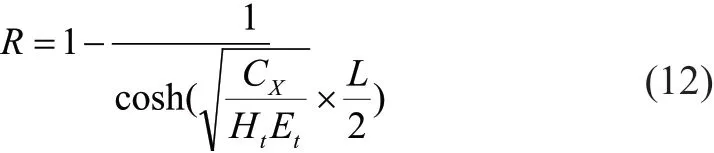
CX——外約束介質(zhì)的水平變形剛度，N/mm3，本節(jié)取 1.5N/mm3；

υ——泊松比，取 0.15；

Ht——考慮徐變影響的松弛系數(shù)，取值見表 14。

表 14 考慮徐變影響的松弛系數(shù)

對于大體積混凝土的瞬時彈性模量：

式中：

E0——28d 齡期的混凝土彈性模量，取值見表 15；

e——2.718。

通過計算可得對應強度等級混凝土的溫度應力見表16。

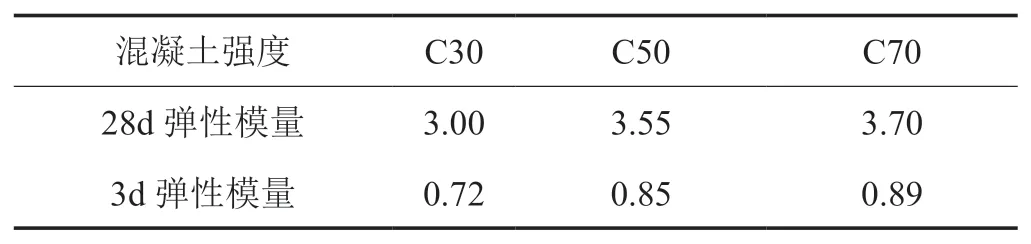
表 15 C30～C70 混凝土彈性模量 104N/mm2

表 16 C30～C70 井壁混凝土溫度應力 MPa

通過計算可得，在膠凝材料的水化放熱的基礎上采用約束系數(shù)法計算所得 C30～C70 井壁混凝土開裂的溫度應力與實測開裂的溫度應力基本接近。

4 結(jié)論

（1）采用考慮了膠凝材料組成的水化放熱模型，對傳統(tǒng)水化放熱量計算公式進行改進，計算得到的水化放熱量與實測水化放熱量的相關性較好。

（2）C30、C50、C70 井壁混凝土試驗絕熱溫升峰值分別為 48℃、57℃、65℃。而基于此的溫度開裂應力為 0.90MPa、1.45MPa 和 1.60MPa。