基于模糊可拓集的特長隧道施工風險評估
王金梁, 王道隆, 陳祖斌, 黃亞娥
(1.中交路橋華南工程有限公司, 廣東 清遠 528400;2.浙江海洋大學, 浙江 舟山 316000)
由于隧道工程的特殊性和復雜性,施工事故發生的可能性較大。特長隧道施工事故一旦發生,將不可避免地造成大量人員和財力損失。為確保隧道施工的可靠性和人員的生命安全,需對隧道施工風險進行準確評估。吳杰等利用模糊隸屬度,通過層次分析法(AHP)計算山區公路隧道施工風險評價指標的權重,并求得各指標層的關聯度。郝德亮等采用AHP法確定隧道主要風險,結合風險矩陣PC法和多級可拓法進行綜合評估。李恒等利用模糊數學理論構造隸屬函數得出模糊一致性判斷矩陣,采用AHP法計算鋼箱梁橋各層評價指標的權重,最終得到鋼箱梁橋的質量等級。馬光金采用故障樹法對盾構隧道施工風險進行分析,使用灰色關聯法對其進行關聯分析,找出需要重視和規避的基本事件并提出預防和處理方案。現有研究大多存在權重確定主觀性過強的問題,且指標值的選取多為實數,而實際工程中參數取值往往是具有模糊性的區間值。采用模糊可拓集方法可對定性指標進行定量化分析。基于此,該文基于AHP法和模糊可拓集理論對特長隧道施工風險進行評估,結合廣東省從化至清遠連州高速公路車子嶺隧道工程進行驗證。
1 建立評估指標體系
分析影響特長隧道施工風險的各種因素,參考現有研究成果,結合車子嶺隧道工程的結構特征,構建表1所示特長隧道施工風險評估指標體系。
2 AHP法確定評價指標權重
2.1 評價尺度
參考文獻[13],得到表2所示評價標準。

表1 特長隧道施工風險評估指標體系

表2 AHP評價尺度
2.2 判斷矩陣
按照層次結構模型,每一層元素都以相鄰上一層次各元素為基準,按表2所示評價尺度各元素為基準,設判斷矩陣為A,有:
(aij)n×n
(1)
按AW=λmaxW求解特征根,并對計算出的W作歸一化處理和一致性檢驗。步驟如下:
(1) 按式(2)計算判斷矩陣每行元素的乘積:
(2)
(2) 按式(3)計算mi的n次方根:
(3)
(4)
(4) 按式(5)計算最大特征根:
(5)
式中:(Aw)i表示向量Aw的第i個分量。
2.3 判斷矩陣一致性檢驗
一致性檢驗公式為:
式中:CI為一致性檢驗指標,CI=(λmax-n)/(n-1);RI為隨機一致性指標,其取值見表3。
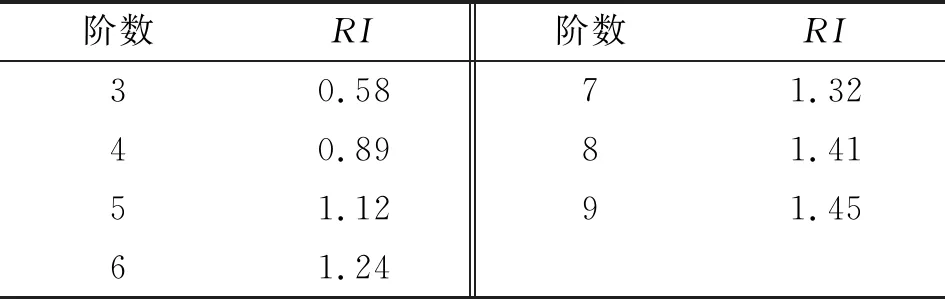
表3 隨機一致性指標的取值
當CI<0.1時,矩陣A符合要求;否則,重新調整取值進行計算,直到滿足一致性檢驗為止。
2.4 計算權重向量
在滿足一致性檢驗的條件下,即可求得各層評估指標的權重向量。
3 構建隧道模糊可拓集綜合評估模型
模糊可拓集綜合評估模型以有序三元組R=(事物,特征,量值)=(N,C,V)作為描述事物的物元,將待評價指標進行定量化分析,然后根據權重計算各指標與評價目標的關聯度,最后根據模糊數學中的最大隸屬度原則得出評價等級。
3.1 確定評價物元模型的經典域與節域
經典域定義為:
(6)
式中:Nj為特長隧道施工風險評估第j(j=1,2,…,m)個等級;ci為特長隧道施工風險評價第i(i=1,2,…,m)個評價指標;vij為隧道施工風險屬于第j個等級時對應ci的指標量值〈aij,bij〉,其為特征ci屬于待評指標的經典域。
節域定義為:
(7)
式中:P為所有特長隧道施工風險評估等級;〈aip,bip〉為某一指標ci的取值范圍,即節域。
3.2 確定隧道施工風險可拓評價物元
隧道施工風險可拓評價物元定義為:
(8)
式中:T為待評價特長隧道施工風險指標;vi為指標量化后的數值。
3.3 指標的無量綱化處理
為使不同單位的評價指標具有可比性,對各層指標進行無量綱化處理。對于越小越好型指標,無量綱化處理公式為:
(9)
對于越大越好型指標,無量綱化處理公式為:
(10)
3.4 計算關聯度
設vik為隧道施工風險關于ci的量值,vij=〈aij,bij〉,vip=〈aip,bip〉,隧道施工風險關于經典域及節域的距為:
(11)
按式(12)計算各指標與評價目標的關聯度:
(12)
3.5 風險評價
根據式(12)所得關聯度及利用式(1)~(5)得到的權重對特長隧道施工風險等級進行可拓評價:
k(Ni)=(wj1,wj2,…,wjk)·
(i=1,2,3)
(13)
k(N)=w1·k(N1)+w2·k(N2)+w3·
k(N3)=(k1(N),k2(N),k3(N),k4(N))
(14)
由模糊數學中最大隸屬度原則,按照式(15)便可確定待評特長隧道施工風險等級。
(15)
4 實例驗證
4.1 工程概況
車子嶺隧道位于清遠英德市水邊鎮境內,進口位于水邊鎮黃泥洞地界,出口位于水邊鎮崩江潭地界。為分離式隧道,左線起訖里程為ZK82+925—ZK84+070,長1 145 m,最大埋深139.3 m;右線起訖里程為K82+910—K84+077,長1 167 m,最大埋深126 m。隧道總體走向方位角約304°。進口、出口均采用端墻式洞門。
4.2 指標權重計算
邀請10位隧道工程領域專家學者對隧道施工風險評價指標的重要性進行打分,根據專家的評分,利用AHP法求出各指標的權重(見表4)。
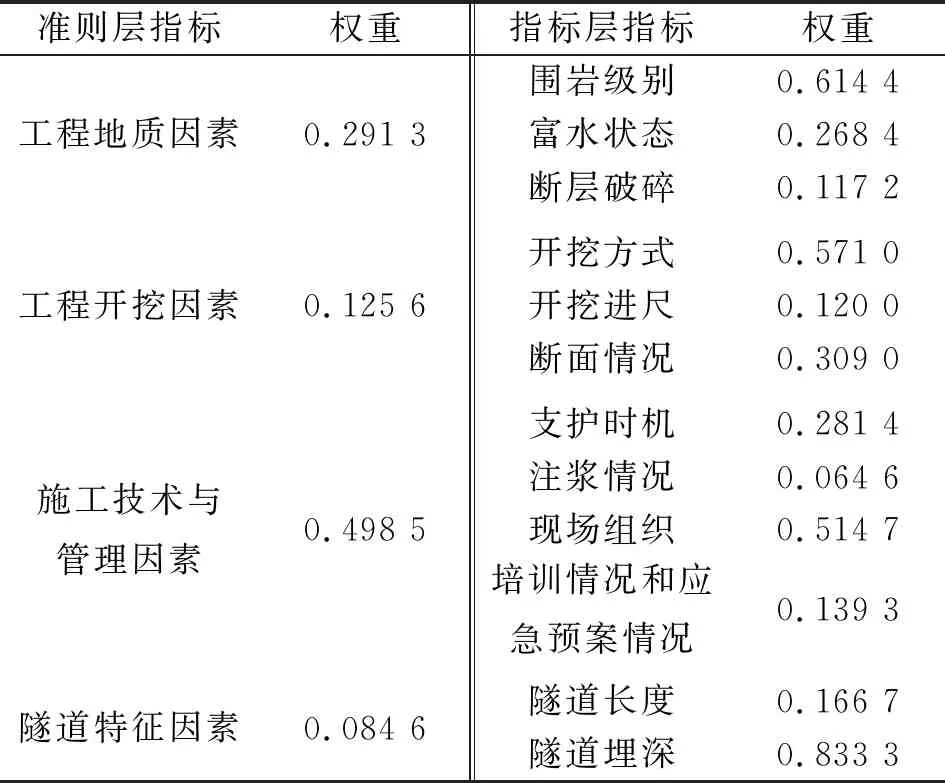
表4 特長隧道施工風險評價指標的權重
4.3 確定風險等級評定標準與分類
將隧道施工風險劃分為4個等級(見表5)。對于定性指標,評價等級Ⅰ、Ⅱ、Ⅲ、Ⅳ級的量化值分別為(0,0.25)、(0.25,0.5)、(0.5,0.75)、(0.75,1.0)。對于定量指標,則進行無量綱化處理,將評價量值劃分到0~1.0內,使各評價指標之間具備可比性。風險指標無量綱化處理前后的結果見表6、表7。

表5 隧道施工風險等級
4.4 確定隧道施工風險物元模型
經典域和節域為:

表6 隧道施工風險評價指標無量綱化前的結果

表7 隧道施工風險評價指標無量綱化處理結果
根據式(11)、式(12)計算各評價指標的風險關聯度,結果見表8。

表8 各評價指標的風險關聯度
4.5 模糊可拓評價
k(N1)=(0.614 4,0.268 4,0.117 2)·
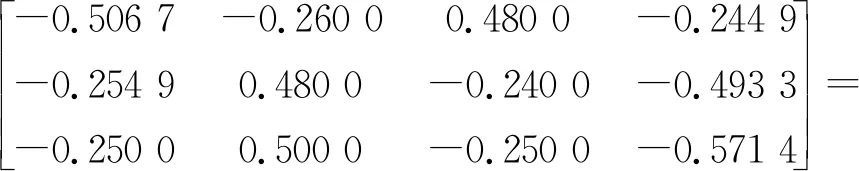
(-0.409 0,0.027 7,0.201 2,-0.349 8)
同理得:
k(N2)=(-0.242 1,0.133 7,-0.078 7,-0.457 3)
k(N3)=(0.123 4,-0.014 1,-0.497 4,-0.664 9)
k(N4)=(0.172 6,-0.172 6,-0.452 8,-0.734 3)
隧道施工風險發生可能性等級的關聯度為:
k(N)=(0.291 3,0.125 6,0.498 5,0.084 6)·

(-0.073 4,0.003 2,-0.237 5,-0.552 9)
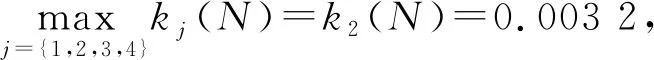
5 結語
該文采用模糊可拓集方法,從工程地質、工程開挖、施工技術與管理和隧道特征4個方面及其12個影響因素進行分析,建立特長隧道施工風險評價指標體系,通過計算指標與評價等級之間的關聯度,準確描述影響隧道施工各因素屬于某一等級的程度,對特長隧道施工風險進行客觀評估。將該模糊可拓集模型應用于廣東省從化至清遠連州高速公路車子嶺隧道工程施工階段安全風險評估,得出風險發生可能性為二級,評估結果與現場實際情況相符,說明該模型具有一定可行性。模糊可拓集評估模型量化了特長隧道施工風險發生可能性,有利于降低其事故發生風險。

