淺析船舶旋回過程及MATLAB仿真

李紀(jì)強(qiáng) 張國慶

（大連海事大學(xué) 航海學(xué)院 大連116026）

引 言

旋回圈幾何參數(shù)是表示船舶旋回性能的重要指標(biāo)，是判斷船舶旋回優(yōu)劣的直接依據(jù)。一般選擇具有實(shí)際意義的特征參數(shù)來描述船舶的旋回性能。IMO操縱性標(biāo)準(zhǔn)中已經(jīng)把進(jìn)距和旋回初徑兩個(gè)參數(shù)作為船舶旋回性能的衡準(zhǔn)。

船舶大型化已是當(dāng)今船舶發(fā)展的一個(gè)趨勢，但是由于大型船舶相對較重且慣性大和停船距離長等特點(diǎn)，其均應(yīng)具備良好的旋回性能。在特殊會(huì)遇情況下，為避免發(fā)生突發(fā)性危險(xiǎn)，大型船舶所采取的避碰措施與普通船舶也存在差異，并且大型船舶在船舶旋回過程中所表現(xiàn)出的較明顯速度下降這一現(xiàn)象，已引起眾多學(xué)者的研究和航海駕駛員在實(shí)際航行中的運(yùn)用。

滿舵旋回是船舶避碰領(lǐng)域中船舶緊急避讓時(shí)經(jīng)常采用的一種避讓方法，因此，研究船舶旋回運(yùn)動(dòng)過程，分析船舶旋回運(yùn)動(dòng)過程中各特征參數(shù)的變化以及旋回速降對于船舶避免碰撞，有一定的實(shí)際意義。Kempf于20世紀(jì)40年代首先提出一種衡量船舶機(jī)動(dòng)性能的試驗(yàn)方法，即Z型試驗(yàn)。此后，在20世紀(jì)50年代，野本謙作和諾賓發(fā)展了一種對Z型試驗(yàn)結(jié)果進(jìn)行理論分析的新方法——

K

、

T

分析法，其中的

K

、

T

指數(shù)可描述船舶操縱性能，所以稱其為操縱性指數(shù)。戴維遜和李宗波等人又根據(jù)大量實(shí)船試驗(yàn)和船模試驗(yàn)繪制了回轉(zhuǎn)速降系數(shù)與相對回轉(zhuǎn)直徑之間關(guān)系的曲線。

1 Nomoto模型與K、T指數(shù)

1.1 Nomoto模型的建立

1.1.1 船舶平面運(yùn)動(dòng)描述

船舶運(yùn)動(dòng)數(shù)學(xué)模型主要建立在兩種坐標(biāo)系上，即慣性坐標(biāo)性和附體坐標(biāo)系，如圖1和圖2所示。

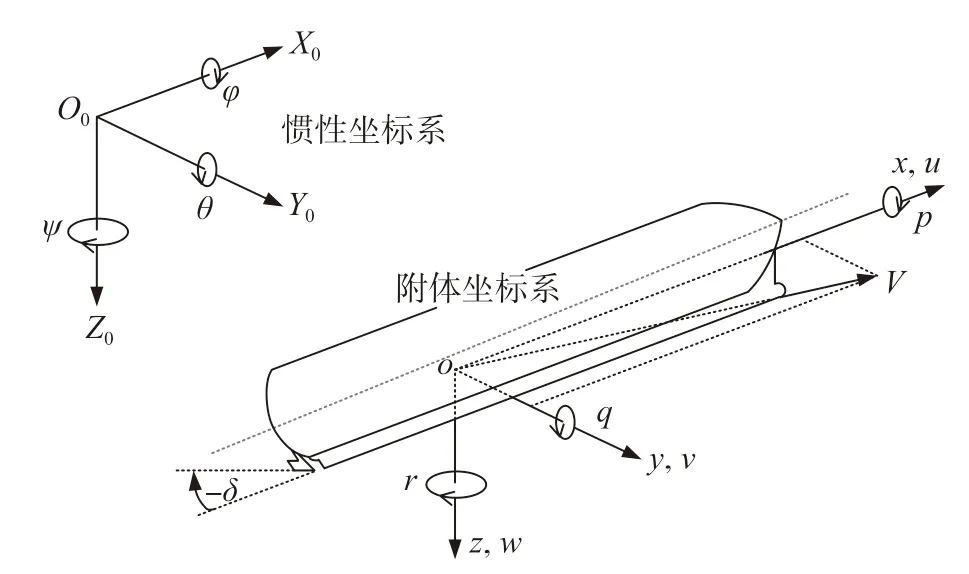
圖1 在慣性坐標(biāo)系和附體坐標(biāo)系中描述船舶的運(yùn)動(dòng)

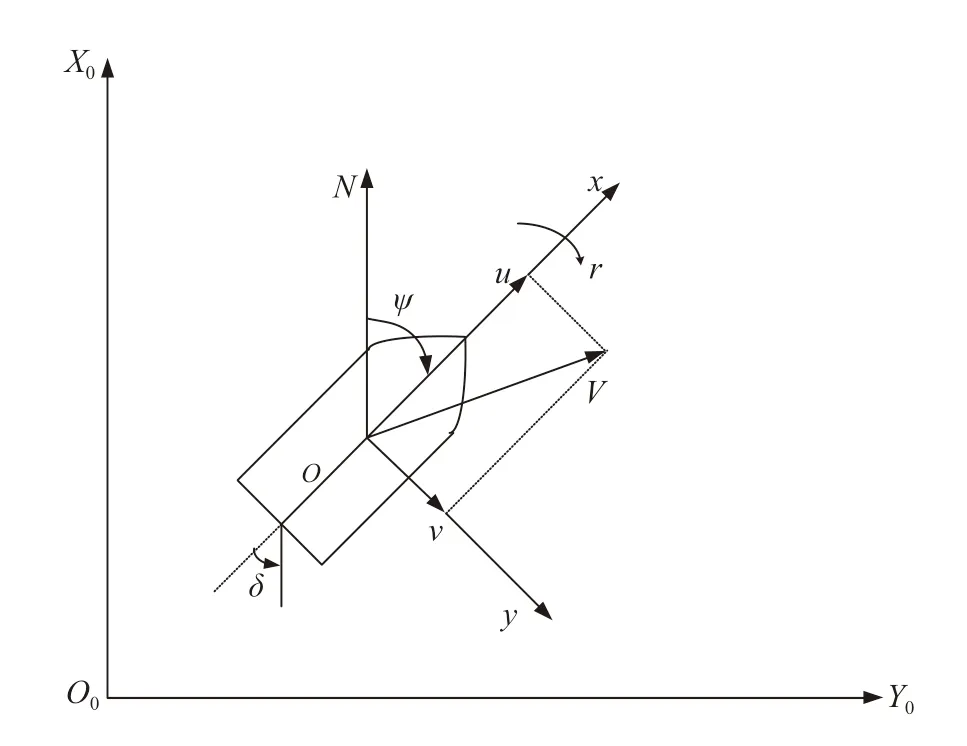
圖2 船舶平面運(yùn)動(dòng)描述

船舶運(yùn)動(dòng)研究通常僅考慮船舶在水平面內(nèi)的運(yùn)動(dòng)，因此船舶的前進(jìn)、艏搖和橫漂三自由度的運(yùn)動(dòng)情況如圖2所示。

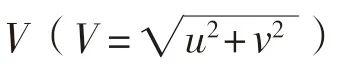
1.1.2 二階響應(yīng)型數(shù)學(xué)模型

船舶水平面操縱運(yùn)動(dòng)的二階響應(yīng)模型是將船舶運(yùn)動(dòng)線性方程的后兩個(gè)式子中的

v

消去，僅考慮船舶的兩個(gè)自由度橫漂速度

v

和轉(zhuǎn)艏角速度

r

，船舶操縱運(yùn)動(dòng)的線性方程如下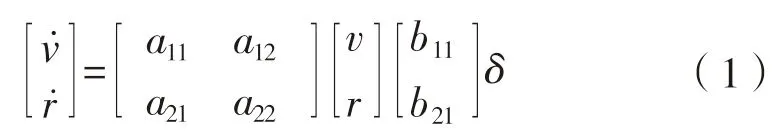

式中：

δ

為舵角輸入，系數(shù)

a

、

a

、

a

、

a

、

b

、

b

由船舶的基本參數(shù)確定。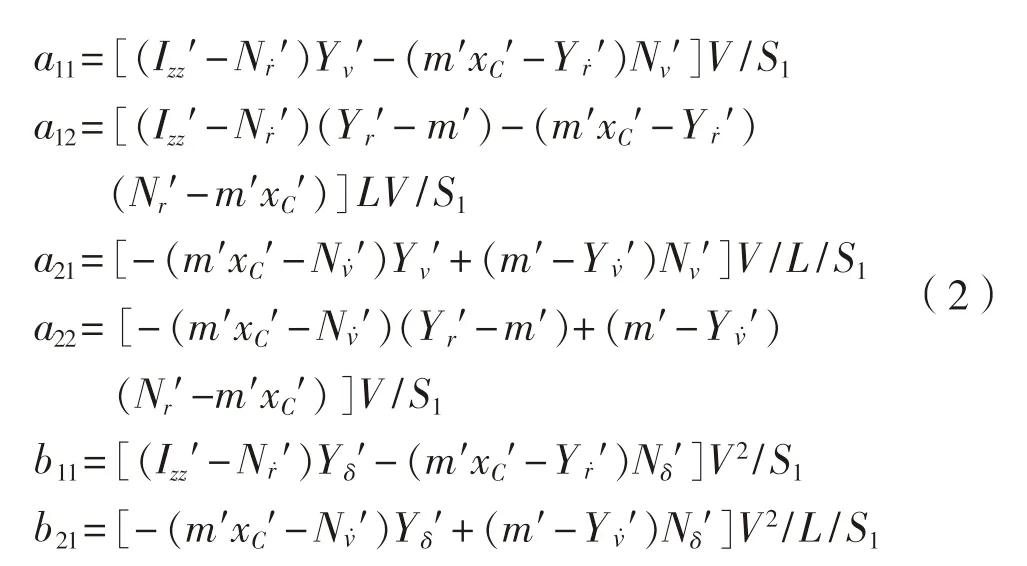

式（1）可轉(zhuǎn)換為一個(gè)描述操舵對艏搖響應(yīng)的簡單方程，即

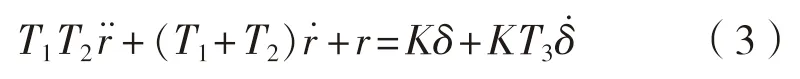
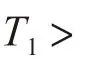
1.1.3 一階響應(yīng)型模型

對式（3）作拉氏變換，可由二階方程推出一階

K

、

T

方程，并設(shè)定初始值為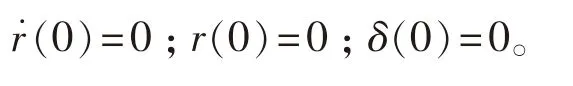

由此可得到船舶轉(zhuǎn)首對操舵響應(yīng)的傳遞函數(shù)

式中：

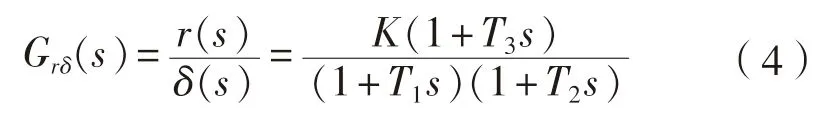
s

為拉普拉斯算子。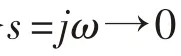

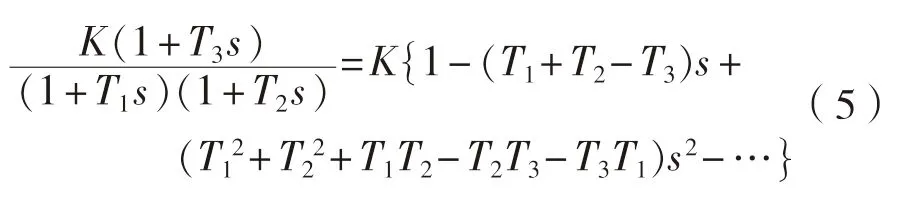
此外，對一階慣性環(huán)節(jié)的傳遞函數(shù)按冪級數(shù)展開，得

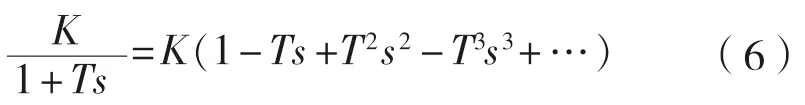
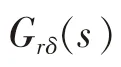
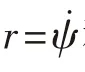
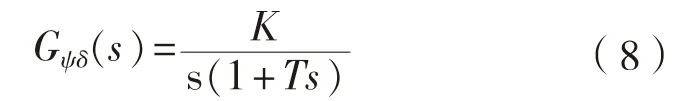
和

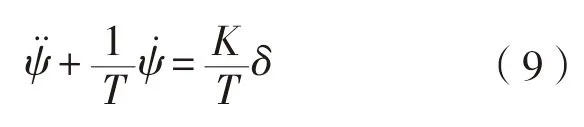
該式等價(jià)于

這就是船舶操縱運(yùn)動(dòng)一階線性

K

、

T

方程（對于

r

來說），也稱為Nomoto模型。

1.2 操縱性指數(shù) K、T

式（10）是描述船舶操縱運(yùn)動(dòng)的簡單實(shí)用方程。野本謙作認(rèn)為，

K

、

T

是一種描述船舶操縱特性的特征參量，具有明確的物理意義。1.2.1 船舶操縱性指數(shù)

K

K

指數(shù)是操舵后轉(zhuǎn)船力矩系數(shù)與阻尼力矩系數(shù)之比所決定的常數(shù)，反映了船舶的旋回性的優(yōu)劣，稱“旋回性指數(shù)”。

K

值越大，表示舵產(chǎn)生的回轉(zhuǎn)力矩大而阻尼力矩小；反之，

K

值越小，表示舵產(chǎn)生的回轉(zhuǎn)力矩越小而阻尼越大。實(shí)際操船中，操船者總是希望

K

值越大越好，表示舵效越好。1.2.2 船舶操縱性指數(shù)

T

T

指數(shù)是船舶繞其重心

G

豎軸的慣性矩與阻尼力矩系數(shù)之比所決定的常數(shù)，代表船舶對舵的快速應(yīng)答性和航向穩(wěn)定性，反映船舶追隨性的優(yōu)劣，稱為“追隨性指數(shù)”。

T

值越大，表示船舶慣性大而阻尼力矩小；反之，

T

值越小，表示船舶慣性小而阻尼力矩大。

T

也被稱為時(shí)間常數(shù)，該時(shí)間越短越好，則舵效越好。所以對于操縱性良好的船舶應(yīng)具有大的正

K

值和小的正

T

值。

2 旋回要素與參數(shù)變化

2.1 旋回圈特征參數(shù)

船舶旋回性最能代表船舶的變向性能，歷史上對旋回性的研究也最多。當(dāng)船舶以速度

u

直線航行時(shí)，操舵后船舶即在水平面內(nèi)作曲線運(yùn)動(dòng)，其軌跡如圖3所示。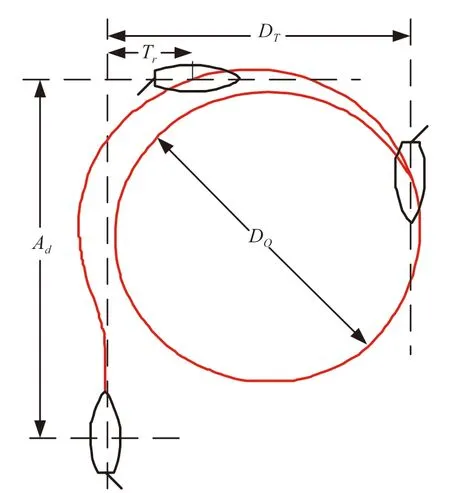

圖3 船舶旋回圈

船舶重心的瞬時(shí)位置為旋回運(yùn)動(dòng)起始點(diǎn)，稱為執(zhí)行操作點(diǎn)。由于船舶慣性較大，艏向角

ψ

需改變一定數(shù)值后，其軌跡才進(jìn)入曲率半徑為常數(shù)的定圓，艏向角再改變一定數(shù)值后，轉(zhuǎn)首角速度才變?yōu)槌?shù)，此時(shí)船舶達(dá)到了定常旋回，旋回圈的主要參數(shù)為：（1）縱距：船舶從旋回開始，艏向轉(zhuǎn)過90

°

時(shí)，船舶重心距離初始位置的縱向距離

A

。該值越大，船舶的旋回性越差。（2）橫距：船舶從旋回開始，艏向轉(zhuǎn)過90

°

時(shí)，船舶重心距離初始航線的長度

T

，該值越小，船舶的旋回性越好。（3）反移量：從船舶初始直航線至運(yùn)動(dòng)軌跡向回轉(zhuǎn)圈相反方向橫移的最大距離

L

，滿舵時(shí)約為船寬的1.0～1.5倍。（4）旋回中的船速

V

：船舶旋回過程中，船速不斷下降，旋回中的船舶速度與初始船舶速度的比值為船舶旋回速降系數(shù)。

2.2 旋回運(yùn)動(dòng)過程分析

從船舶運(yùn)動(dòng)學(xué)角度考察船舶的旋回運(yùn)動(dòng)，其運(yùn)動(dòng)過程可分為3個(gè)階段，即轉(zhuǎn)舵階段、過渡階段和定常旋回階段。旋回運(yùn)動(dòng)過程中運(yùn)動(dòng)參數(shù)的變化如圖4所示。

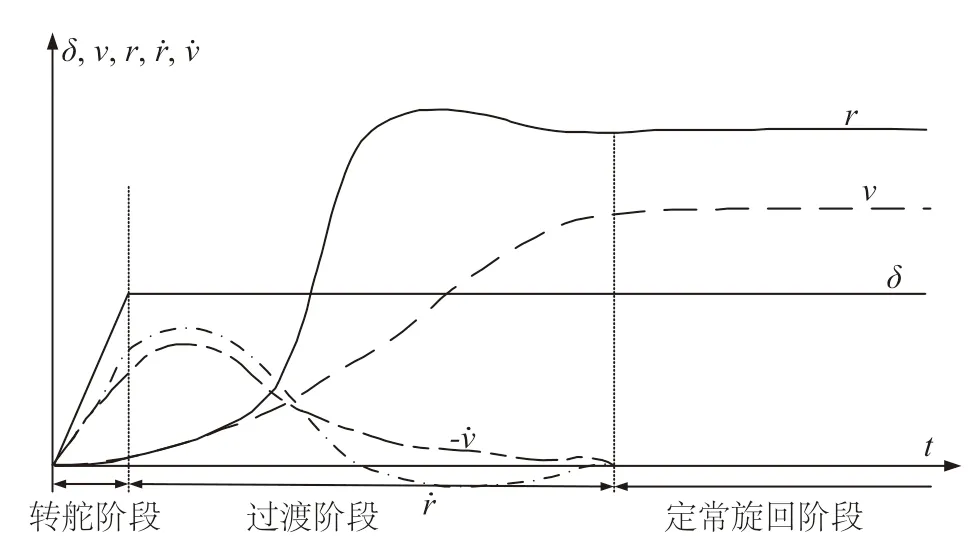
圖4 旋回運(yùn)動(dòng)過程中運(yùn)動(dòng)參數(shù)的變化

2.2.1 初始階段

在舵角達(dá)到規(guī)定值之前為船舶旋回初始階段。在此階段，船舶發(fā)生內(nèi)傾，產(chǎn)生各自由度的加速度和速度及角速度，在操右舵時(shí)，舵橫向力的方向?yàn)樨?fù)（向左），轉(zhuǎn)舵力矩的方向?yàn)檎担槙r(shí)針），且由于船舶慣性較大，因此船舶在此階段基本保持原直線運(yùn)動(dòng)。

2.2.2 過渡階段

在過渡階段，舵角達(dá)到（

δ

）且不變，船舶前進(jìn)、橫漂、艏搖等自由度上均存在加速度和速度，且加速度在不斷變化，船舶發(fā)生外傾。

2.2.3 定常階段

在船舶旋回過程中，在經(jīng)過一段時(shí)間后，船舶各自由度上加速度均為0，速度和角速度為一定常量，此時(shí)，船舶進(jìn)入定常旋回階段。

2.3 旋回過程速降研究

在船舶旋回運(yùn)動(dòng)過程中，會(huì)產(chǎn)生船舶運(yùn)動(dòng)速度降低的現(xiàn)象。其原因之一是由于旋回運(yùn)動(dòng)過程中，橫向速度

v

和角速度

r

的存在使船舶處于斜航和和旋轉(zhuǎn)狀態(tài)，船舶阻力比直航時(shí)大為增加；其原因之二是由于螺旋槳通常設(shè)計(jì)為直航狀態(tài)時(shí)的推進(jìn)效率最高，而船舶旋回過程中

v

、

r

、

δ

的存在使螺旋槳推進(jìn)效率大為降低。另外，船舶旋回過程中由于阻力的增大，螺旋槳轉(zhuǎn)速也會(huì)相應(yīng)降低。因此，這些因素都導(dǎo)致船舶旋回運(yùn)動(dòng)過程中的船速下降，稱為“旋回速降”。

船舶旋回速降與初始船速、船型、載況等諸多因素有關(guān)。萬噸級船舶一般旋回降速達(dá)25%～50%，大型船舶旋回速降更為劇烈，有時(shí)甚至可達(dá)65%以上。

李宗波等人在研究了國內(nèi)外關(guān)于速降系數(shù)的研究后，綜合了速降系數(shù)的影響因素可以取3個(gè)代表性的因素來衡量，分別為旋回性指數(shù)

K

′、舵的法向力系數(shù)

C

和航向改變量Δ

ψ

。在43艘船舶的基礎(chǔ)上，李宗波等人又搜集了4艘超大型船的

K

′、

T

′指數(shù)資料，利用47艘船的資料回歸分析得到修訂的

K

′、

T

′估算公式為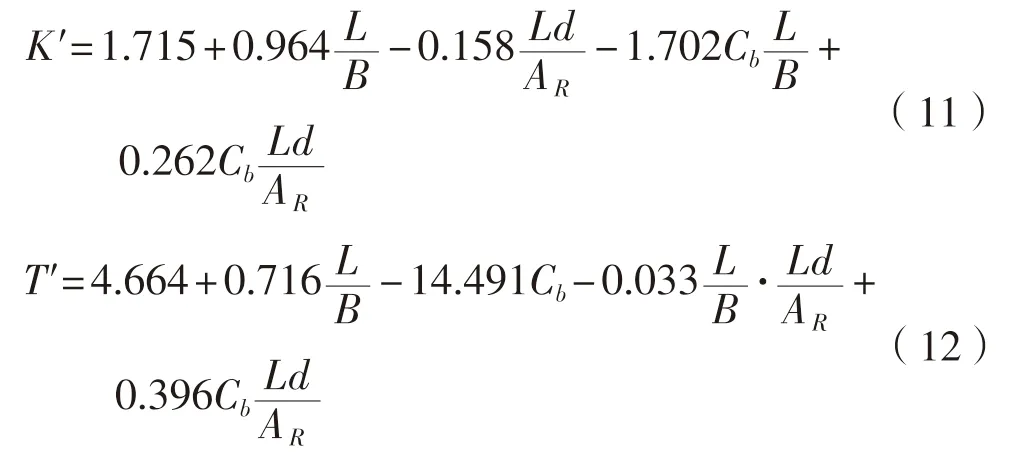

式中：

L

、

B

、

d

分別為船長、船寬和吃水，m；

A

為舵面積，m；

C

為方形系數(shù)。修訂后的

K

′、

T

′估算公式的擬合優(yōu)度指標(biāo)即復(fù)相關(guān)系數(shù) 略有增加，分別達(dá)到了0.792和0.851。由修正后的

K

′、

T

′，進(jìn)行多次最優(yōu)回歸分析，可以得到船舶旋回速降系數(shù)估算公式。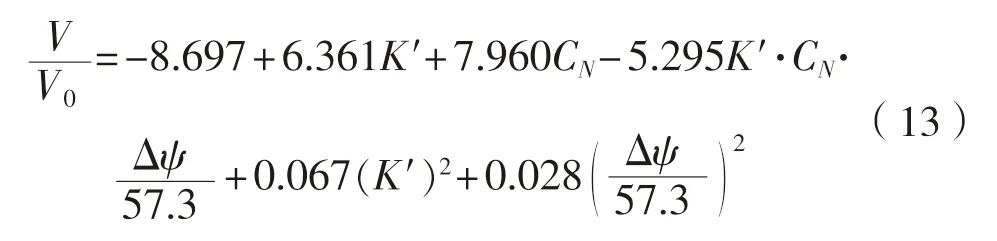

式中：Δ

ψ

的單位為（°）。

表1 給出了OPALIA輪壓載狀態(tài)下滿舵旋回試驗(yàn)中的速降記錄結(jié)果。可見定常旋回時(shí)的船速約為初始船速的1/5，同樣，旋回方向?qū)π亟邓儆绊懖淮蟆?/p>

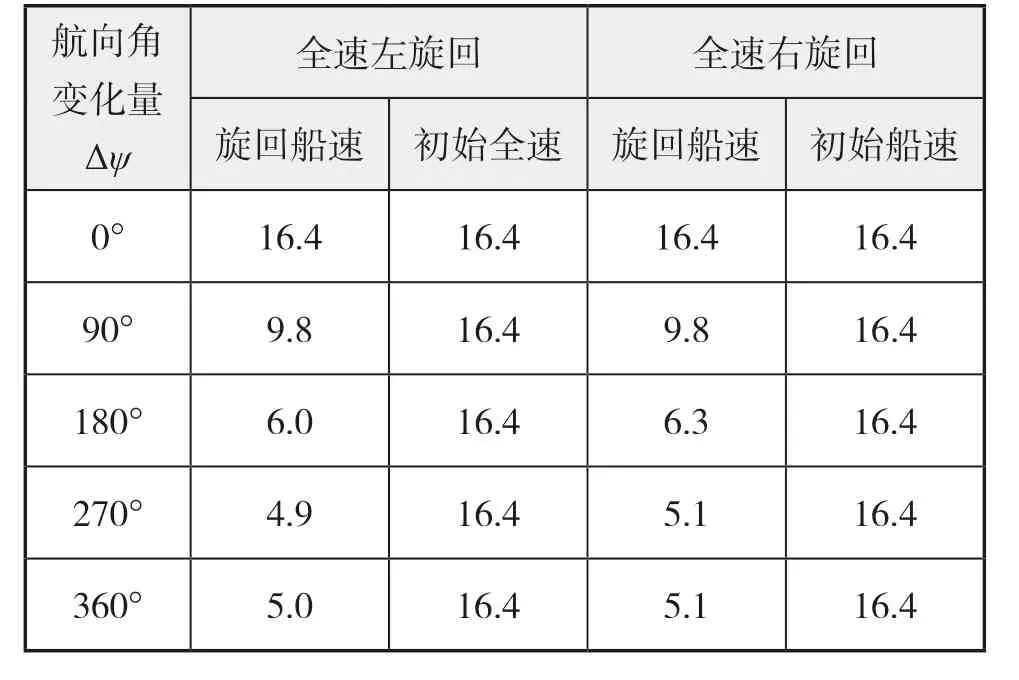
表1 OPALIA輪壓載狀態(tài)下的速降記錄kn

本文采用李宗波等人提出的速降估算公式，對30萬噸油輪OPALIA輪進(jìn)行MATLAB仿真驗(yàn)證并與實(shí)船結(jié)果進(jìn)行比較，驗(yàn)證了對于李宗波等人研究結(jié)果對超大型船舶旋回速降的預(yù)報(bào)性。進(jìn)行了壓載狀態(tài)下全速滿舵（

δ

= 35

°

）旋回的速降預(yù)報(bào)。該輪主尺度為：兩柱間長

L

= 320 m、船寬

B

= 60 m；試驗(yàn)時(shí)，平均吃水

d

= 10.660 m、方形系數(shù)

C

= 0.743 4，舵面積比

A

/（

Ld

）=1/35.04。經(jīng)式（12）計(jì)算得到

K

′=1.396 6；舵角35

°

時(shí)，舵的法向力系數(shù)

C

=1.257 4。圖5和圖6分別表示OPALIA輪在壓載左滿舵和壓載右滿舵（

δ

= 35

°

）情況下的旋回速降實(shí)驗(yàn)對比圖。圖中：藍(lán)色實(shí)線表示旋回速降的實(shí)時(shí)預(yù)報(bào)，黑色離散點(diǎn)表示OPALIA輪在實(shí)際旋回實(shí)驗(yàn)中監(jiān)測到的旋回速降數(shù)值。從圖5和圖6可以看出，旋回速降預(yù)報(bào)曲線和實(shí)際速降數(shù)值變化曲線基本一致，由此說明旋回速降預(yù)報(bào)公式的有效性。

圖5 OPALIA輪壓載左滿舵（35°）旋回速降圖

圖6 OPALIA輪壓載右滿舵（35°）旋回速降圖

2.4 旋回試驗(yàn)與MATLAB仿真

本節(jié)利用MATLAB仿真響應(yīng)型數(shù)學(xué)模型，試驗(yàn)對象為大連海事大學(xué)教學(xué)實(shí)習(xí)船“育鯤輪”。本節(jié)考慮航海仿真條件給出了基于“育鯤輪”的仿真測試結(jié)果，外界環(huán)境干擾等效為式（14）。

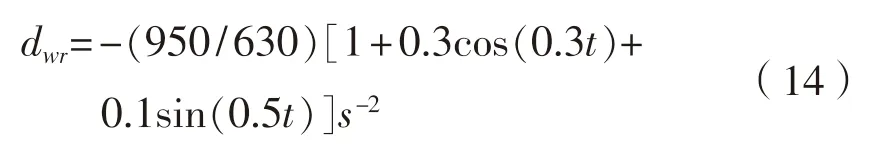
圖7表示旋回試驗(yàn)MATLAB仿真流程圖。

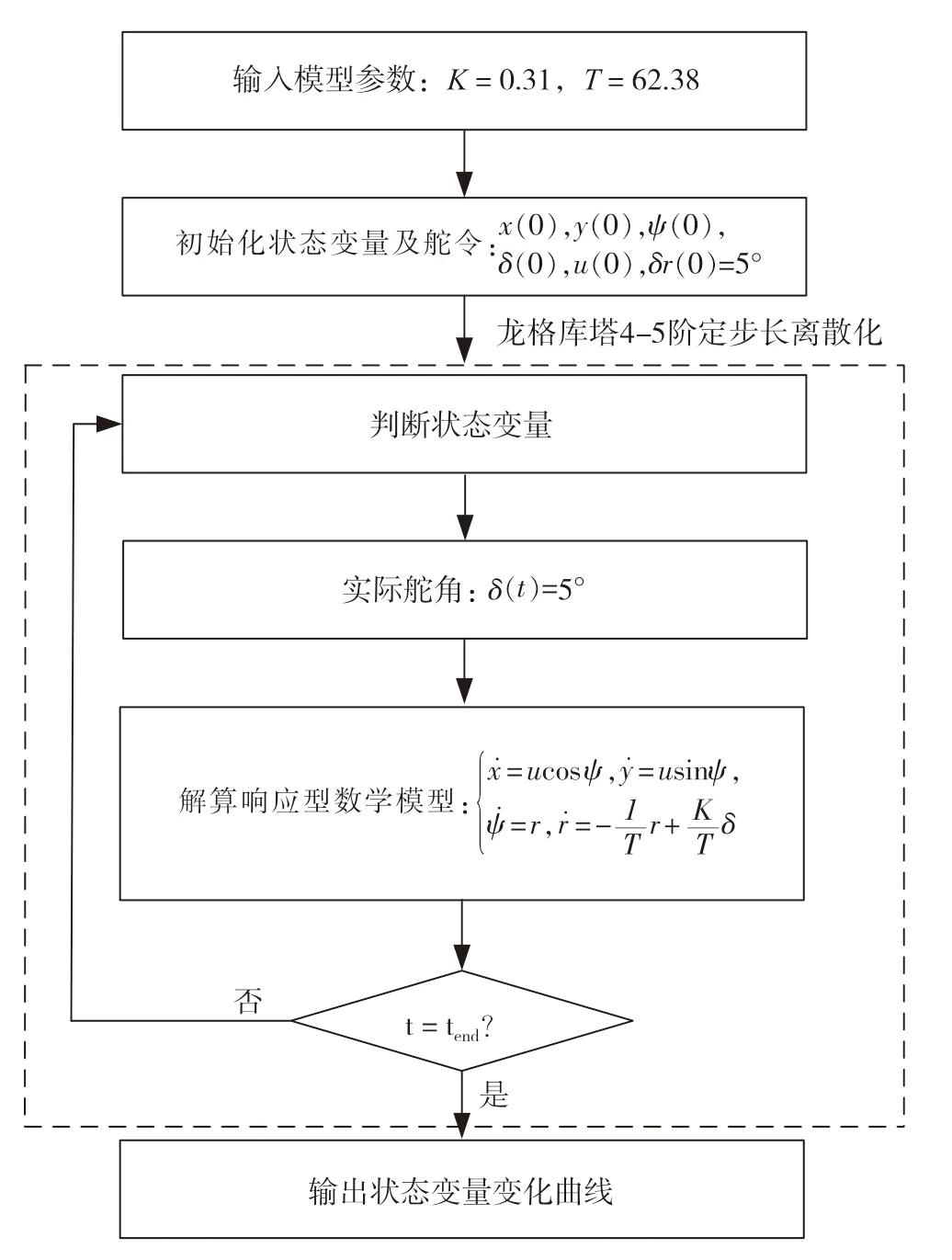
圖7 旋回試驗(yàn)MATLAB仿真流程圖

在船舶定速直航狀態(tài)下，當(dāng)轉(zhuǎn)舵角

δ

= 5

°

時(shí)，圖8、圖9和圖10給出了船舶旋回運(yùn)動(dòng)的仿真結(jié)果。從圖8可以看出，航向

ψ

、

r

在200 s之內(nèi)非線性增大，在200 s之后，船舶進(jìn)入定常旋回階段，航向勻速增大到360

°

，轉(zhuǎn)艏角速度穩(wěn)定在1.5

°

/s。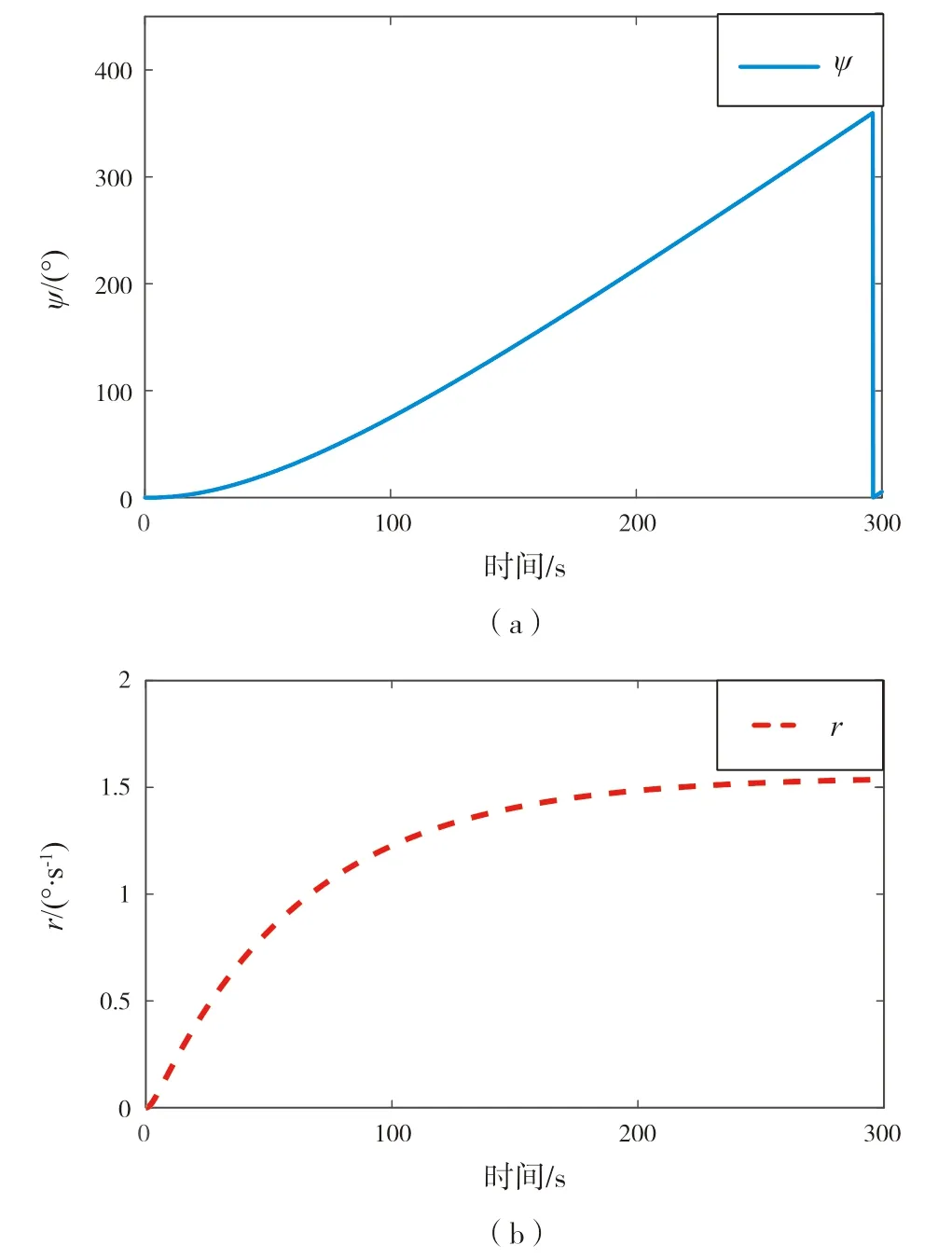

圖8 旋回試驗(yàn)r，ψ-t仿真曲線

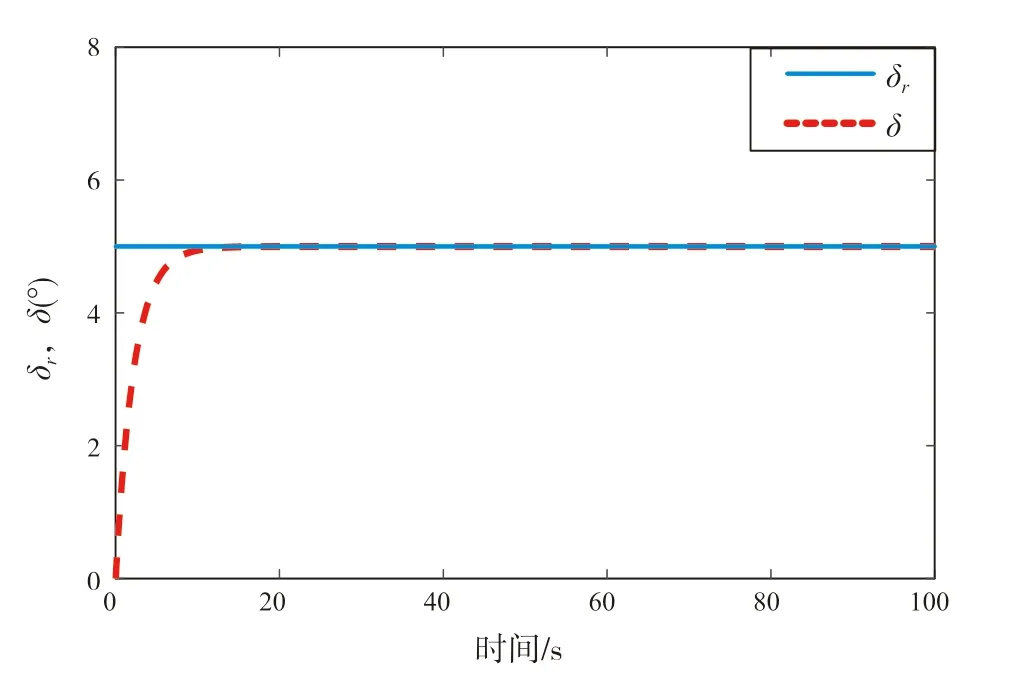
圖9 旋回試驗(yàn)δr，δ-t仿真曲線

圖9舵機(jī)伺服系統(tǒng)可以看出，命令舵角

δ

與實(shí)際舵角

δ

之間的關(guān)系：在初始一段時(shí)間內(nèi)，實(shí)際舵角

δ

非線性增大；在15 s后，實(shí)際舵角

δ

與命令舵角

δ

達(dá)到一致。圖10給出船舶旋回運(yùn)動(dòng)軌跡圖。當(dāng)命令右舷舵角5

°

時(shí)，船舶重心在縱軸方向發(fā)生移動(dòng)，這段距離即圖注

A

；此外，可見船舶旋回圈，而旋回圈直徑（

D

）大小，將會(huì)反映定常旋回過程中占用水域的范圍。由圖10可見，旋回直徑約是實(shí)際船長的5倍左右。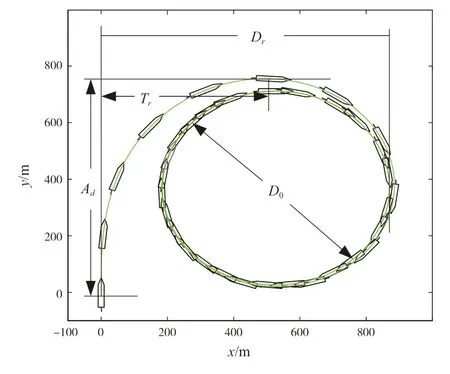

圖10 旋回試驗(yàn)船舶運(yùn)動(dòng)仿真軌跡圖

3 結(jié) 論

本文針對船舶旋回運(yùn)動(dòng)過程進(jìn)行研究，分析了旋回過程中的3個(gè)階段，并且針對旋回過程中的速降問題進(jìn)行深入分析，利用速降估算公式對“OPALIA”輪壓載狀態(tài)下的左滿舵與右滿舵旋回速降進(jìn)行預(yù)報(bào)，并與實(shí)際速降曲線進(jìn)行對比，結(jié)果驗(yàn)證了速降估算公式的準(zhǔn)確性。最后，在模擬海洋干擾環(huán)境下，采用龍格庫塔4-5階定步長離散化的方法，對“育鯤”輪進(jìn)行MATLAB旋回仿真試驗(yàn)。仿真結(jié)果顯示，旋回直徑約為實(shí)際船長的5倍，這與實(shí)際工況相符，進(jìn)一步說明了仿真試驗(yàn)的有效性與準(zhǔn)確性。

本文尚存在以下不足：

（1） 船舶運(yùn)動(dòng)數(shù)學(xué)模型采用最簡潔的Nomoto模型，該模型存在不足；

（2） 船舶旋回速降影響因素較多，沒有確切的數(shù)學(xué)模型，因此，本文采用的速降估算公式尚存在一定誤差。