山區(qū)公路隧道拱頂沉降回歸模型的比選

魏弘銘， 范 瑛

(湖北工業(yè)大學(xué)土木建筑與環(huán)境學(xué)院， 湖北 武漢 430068)

山區(qū)公路隧道在其施工階段中隧道拱頂沉降現(xiàn)象是一個(gè)多變復(fù)雜的非線性過程，對其變化量進(jìn)行準(zhǔn)確的預(yù)測與評(píng)估具有非常重要的工程意義。業(yè)界多采用半經(jīng)驗(yàn)法、線性和非線性多元回歸分析法對拱頂沉降監(jiān)測數(shù)據(jù)建立多種模型，來分析預(yù)判新奧法施工的隧道拱頂產(chǎn)生的沉降值[1]。在隧道施工過程中，因環(huán)境復(fù)雜、監(jiān)測儀器以及操作誤差等多重因素的影響，常常會(huì)使得拱頂沉降監(jiān)測數(shù)據(jù)不完全，因此單憑監(jiān)測數(shù)據(jù)很難對拱頂沉降現(xiàn)象作出準(zhǔn)確判斷與評(píng)價(jià)。本文以山區(qū)公路隧道拱頂沉降監(jiān)測數(shù)據(jù)為基礎(chǔ)，建立變量，對數(shù)據(jù)進(jìn)行處理，建立回歸模型，研究分析監(jiān)測數(shù)據(jù)存在的規(guī)律，具有科學(xué)、簡便、實(shí)用性強(qiáng)的特點(diǎn)。具體做法是：依托竹山縣西溝埡隧道工程，對監(jiān)測數(shù)據(jù)進(jìn)行處理，采用4種回歸函數(shù)建立回歸模型，通過顯著性檢驗(yàn)和回歸曲線擬合對每一種回歸模型進(jìn)行比選，確定最適宜的回歸模型，為西溝埡隧道拱頂沉降量分析預(yù)判提供科學(xué)依據(jù)，指導(dǎo)隧道施工。

1 工程概況

西溝埡隧道位于242國道竹山縣上庸鎮(zhèn)田家壩至峪口段改擴(kuò)建工程的K4+025處，為新建單洞式隧道，隧道起止里程樁號(hào)為K3+765-K4+285，隧道全長520 m，最大埋深約102 m，建筑限界有效凈高5.0 m，有效凈寬10.0 m，凈空斷面面積為58.79 m2。勘察區(qū)域地貌單元屬鄂西北構(gòu)造侵蝕中高山區(qū)，山體起伏較大，地表植被較好，最大高程位于山頂，最低位置處于溝谷，相對高差約100 m，隧道區(qū)域山脊總體走向?yàn)楸睎|西向，隧道軸線呈西北南向穿過山脊。西溝埡隧道從隧道進(jìn)口處單向開挖，隧道施工按照新奧法原理，短臺(tái)階法作業(yè)。

2 顯著性檢驗(yàn)

2.1 相關(guān)系數(shù)

變量x和變量y之間是否存在線性關(guān)系，若存在線性關(guān)系那么線性關(guān)系程度的大小用相關(guān)系數(shù)r表示，即

相關(guān)系數(shù)r按三級(jí)標(biāo)準(zhǔn)劃分：|r|<0.4為低度線性相關(guān)；0.4≤|r|<0.7為顯著性相關(guān)；0.7≤|r|<1為高度線性相關(guān)[1]。

2.2 回歸估計(jì)標(biāo)準(zhǔn)誤差

通過回歸模型得到的回歸值與實(shí)際值之間偏離程度大小的指標(biāo)用回歸估計(jì)標(biāo)準(zhǔn)誤差σ表示，即

σ值越小，回歸值與其實(shí)際值的近似誤差越小，回歸值的代表性越強(qiáng)，用回歸模型預(yù)測的結(jié)果越精確，回歸模型的代表性越強(qiáng)[1]。

2.3 回歸平方和U

回歸平方和U表示，即

2.4 方差齊性檢驗(yàn)

顯著性水平α給定，本文選取α=0.05，計(jì)算F值，通過F值分布表比較。若F>F(1，n-2)，說明變量x與變量y有顯著的線性關(guān)系，若F≤F(1，n-2)，則稱變量x與y沒有明顯的線性關(guān)系，說明回歸模型效果不顯著，不具有代表性。

3 回歸模型建立

回歸模型就是基于已有的數(shù)據(jù)構(gòu)建數(shù)學(xué)統(tǒng)計(jì)模型，得出變量之間關(guān)系的近似表達(dá)式，并根據(jù)表達(dá)式對相應(yīng)的變量進(jìn)行預(yù)測等[1]。

3.1 數(shù)據(jù)處理

選取測點(diǎn)穩(wěn)定、無損壞、監(jiān)測數(shù)據(jù)較完整的監(jiān)測斷面進(jìn)行拱頂沉降回歸模型的建立。西溝埡隧道拱頂監(jiān)測斷面布置較多，僅以樁號(hào)為K4+190的監(jiān)測斷面拱頂沉降數(shù)據(jù)為例，對回歸模型的建立進(jìn)行分析研究。在回歸模型建立過程中，選擇自變量為監(jiān)測時(shí)間，拱頂累計(jì)沉降量為因變量。

回歸模型的建立對奇異值非常敏感，奇異值的存在會(huì)極大地影響回歸模型的效果以及后期拱頂沉降預(yù)測值，而在實(shí)際情況下，監(jiān)測數(shù)據(jù)又容易受到多重因素影響而出現(xiàn)較大的波動(dòng)起伏，因此在回歸模型建立前，需對監(jiān)測數(shù)據(jù)中的奇異值進(jìn)行處理以提高回歸模型的精度[3]。對于奇異值我們采用“拉依達(dá)準(zhǔn)則”檢驗(yàn)法找出剔除，并采用鄰點(diǎn)中值法進(jìn)行替換。

1)“拉依達(dá)準(zhǔn)則”檢驗(yàn)法

“拉依達(dá)準(zhǔn)則”檢驗(yàn)法又稱為“3σ準(zhǔn)則”檢驗(yàn)法，對于一組數(shù)據(jù){y1，y2，…，yi-1}，我們定義該組數(shù)據(jù)di：

di=2yi-(yi-1+yi+1)i=1,2,3,…,n-2

當(dāng)qi>3時(shí)，則認(rèn)為yi是奇異值[4]，應(yīng)舍棄，空位值采用鄰點(diǎn)中值代替。

2)鄰點(diǎn)中值法

選擇奇異值點(diǎn)兩側(cè)相鄰點(diǎn)的數(shù)據(jù)yi-1和yi+1的中點(diǎn)值作為新的數(shù)據(jù)，新點(diǎn)yi計(jì)算公式為：

經(jīng)過處理后的拱頂沉降數(shù)據(jù)如表1所示。

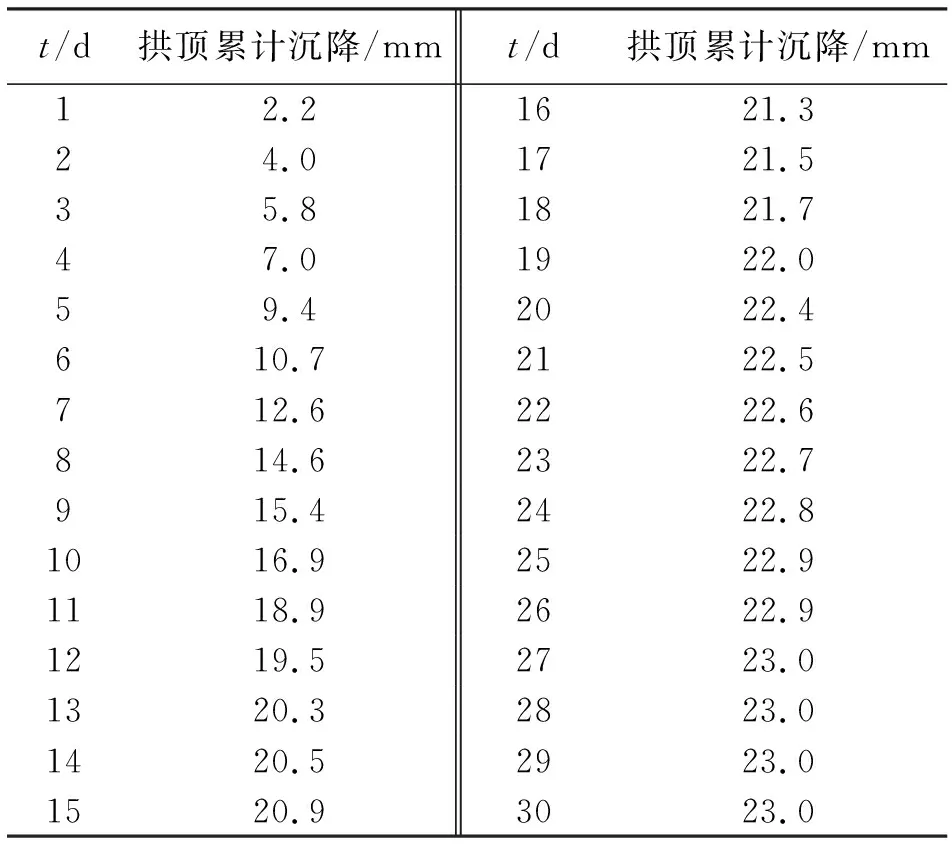
表1 隧道K4+190監(jiān)測斷面隨時(shí)間變化拱頂累計(jì)沉降值

3.2 回歸方程確定

根據(jù)JTGF60-2009《公路隧道施工技術(shù)規(guī)范》[5]的相關(guān)要求本文將分析下列4種回歸函數(shù)模型的擬合效果：

冪函數(shù)模型

U=AtB

指數(shù)函數(shù)模型

U=Aexp(-B/t)

對數(shù)函數(shù)模型

U=A+Blg(1+t)

雙曲線函數(shù)模型

U=t/A+Bt

式中：A，B為回歸常數(shù)；U為拱頂累計(jì)沉降值,mm；t為初始沉降后的時(shí)間,d。

通過最小二乘法計(jì)算各回歸模型參數(shù)，最小二乘估計(jì)法的思想就是對于每一個(gè)樣本觀察值(xi，yi)，使得觀察值yi與f(xi)在該點(diǎn)處的誤差平方和最小[6]。對于一元非線性函數(shù)模型，通過變量代換， 把一元非線性函數(shù)轉(zhuǎn)換為一元線性函數(shù)y=a+bx，再利用最小二乘法計(jì)算參數(shù)a、b，通過a、b換算出曲線函數(shù)常數(shù)A、B值[7]。本文以指數(shù)函數(shù)模型U=Ae-B/t為例進(jìn)行計(jì)算分析。

指數(shù)函數(shù)模型，表達(dá)式U=Ae-B/t，采用換元法，令y=lnU，a=lnA，b=B，x=-1/t，得轉(zhuǎn)換函數(shù):y=a+bx，對系數(shù)a、b采用最小二乘法算出，如下式所示：

(i=1,2,3,…,n=30)

(i=1,2,3,…,n=30)

求出回歸方程表達(dá)式見下表，用同樣的方法可得出冪函數(shù)模型、對數(shù)函數(shù)模型、雙曲函數(shù)模型的回歸方程表達(dá)式，計(jì)算過程見表2。

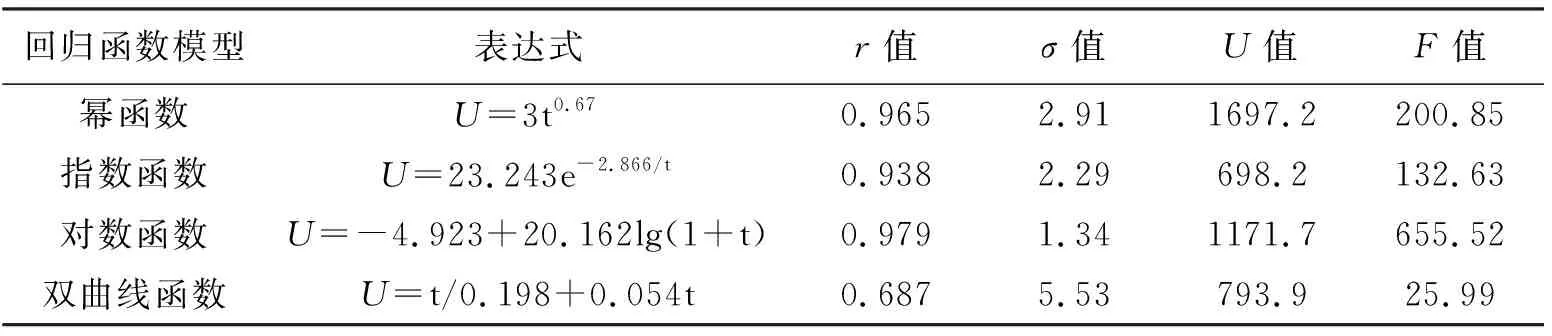
表2 回歸函數(shù)模型表達(dá)式及相關(guān)參數(shù)統(tǒng)計(jì)表

4 回歸模型的比選

4.1 回歸曲線

回歸曲線：兩變量間呈現(xiàn)曲線關(guān)系的回歸，確定兩變量間數(shù)量變化的某種特定的規(guī)則或規(guī)律。各回歸模型所對應(yīng)的回歸曲線與拱頂累計(jì)沉降量-時(shí)間實(shí)測曲線擬合圖見圖1～4。

圖 1 冪函數(shù)模型回歸曲線

圖 2 指數(shù)函數(shù)模型回歸曲線

圖 3 對數(shù)函數(shù)模型回歸曲線

圖 4 雙曲線模型回歸曲線

對比分析圖1～4所示的回歸曲線，對數(shù)函數(shù)模型是曲線擬合效果最好的，結(jié)合顯著性檢驗(yàn)中的相關(guān)系數(shù)r值、回歸估計(jì)標(biāo)準(zhǔn)誤差σ值、回歸平方和U值、F檢驗(yàn)值，在回歸平方和U值比選方面，雖然冪函數(shù)模型U值大于對數(shù)函數(shù)模型U值，但綜合各指標(biāo)值以及回歸曲線擬合趨勢，顯然對數(shù)函數(shù)模型能夠更好地?cái)M合實(shí)測數(shù)據(jù)，與實(shí)測數(shù)據(jù)相關(guān)度更高，所以最終確定對數(shù)函數(shù)模型為西溝埡隧道拱頂沉降評(píng)價(jià)分析模型，在后續(xù)西溝埡隧道施工過程中，采用對數(shù)函數(shù)模型，對拱頂沉降量進(jìn)行預(yù)測分析評(píng)價(jià)以及合理確定二襯施作時(shí)間。

4.2 實(shí)測對比驗(yàn)證

通過顯著性檢驗(yàn)以及回歸曲線擬合比選后得到的回歸模型，在具體應(yīng)用于實(shí)際分析前，要將回歸模型與實(shí)際數(shù)據(jù)再一次對比驗(yàn)證，將t=18，19，…，26代入對數(shù)函數(shù)回歸方程中，得出對應(yīng)的拱頂沉降回歸值，并與實(shí)際值進(jìn)行對比，得到實(shí)際值與回歸值對比表，見表3。

表3 實(shí)際值與回歸值對比表

通過對數(shù)函數(shù)回歸模型預(yù)測出隧道拱頂沉降在開始監(jiān)測的第19 d后趨于基本穩(wěn)定， 實(shí)測結(jié)果為第21 d以后趨于基本穩(wěn)定，實(shí)測結(jié)果與預(yù)測結(jié)果基本對應(yīng)，體現(xiàn)出回歸模型分析結(jié)果的可靠性。回歸相對偏差率=(回歸值-實(shí)測值)/實(shí)測值，通過計(jì)算，回歸相對偏差率在-0.03%～5.45%范圍之間，偏差較小，對數(shù)函數(shù)模型得到的回歸值與實(shí)測結(jié)果值吻合度較好，可以用于西溝埡隧道拱頂沉降現(xiàn)象的評(píng)價(jià)分析以及施工過程中沉降量的預(yù)測。

5 結(jié)論

1)利用4種回歸函數(shù)對西溝埡隧道樁號(hào)為K4+190的監(jiān)測斷面進(jìn)行拱頂沉降回歸模型的比選，比選結(jié)果顯示，4種回歸函數(shù)模型中對數(shù)函數(shù)回歸模型代表性最強(qiáng)，與實(shí)際情況吻合度更好，同時(shí)也表明各回歸模型的適用性不同，應(yīng)根據(jù)具體工程實(shí)際選擇回歸模型。

2)判斷某一回歸模型的優(yōu)劣要從相關(guān)系數(shù)、回歸差、回歸平方和、F值、回歸曲線與實(shí)測曲線擬合趨勢等幾個(gè)方面綜合分析考慮，單一因素往往是片面的，不具代表性。

3)為了能夠更好的分析評(píng)價(jià)隧道拱頂沉降現(xiàn)象，有些測點(diǎn)監(jiān)測數(shù)據(jù)可能采用幾種回歸模型的組合，某一部分用一種回歸模型，另一部分用另外一種回歸模型，這樣得到的結(jié)果可能更符合實(shí)際情況，這種組合模型在日后的運(yùn)用過程中仍需深入分析探討。