低頻振動鉆削鈦合金板的非線性分析與應用*

侯書軍，裴騰飛，李 慨，曲云霞，李 坤，李 凱

（河北工業大學機械工程學院 天津，300130）

引言

由于鈦合金在比強度、比剛度等方面的諸多優勢，使其在航空制造領域得到了日益廣泛的應用［1］，如波音787機身結構材料的15%都采用了鈦合金［2］。鈦合金常與碳纖維組成復合材料疊層并通過鉚接形成結構，該類復合材料的高精度制孔是保證連接強度與結構性能的主要因素之一［3］。而鈦合金在機械性能方面的優勢，加之其導熱率低，給本就切削效率較低的鉆孔作業帶來了很大挑戰。比如在用普通鉆進行鈦合金板鉆孔時極易產生高溫螺旋長屑，不僅劃傷自身孔面也灼傷碳纖維層，從而影響孔加工表面的質量［4］。因此，如何有效斷屑成為該技術研究的核心課題。

近年來，有人借助超聲振動進行改善鈦合金斷屑的研究。邵振宇等［5］應用超聲輔助鉆削技術進行了鈦合金鉆削試驗，說明了超聲鉆削可以降低鉆削力，提高刀具切削能力，獲得良好的斷屑與排屑效果。但也有研究認為超聲振動雖然可以降低切削力，但卻會引起切削溫度的升高［6］。從材料特性的角度看，鈦合金屬于塑性極強的高強度材料，而振動的目的就在于破壞切屑的連續性，此時低頻較大振幅的振動應該更加合適。在此方面，法國的“mitis”系統獲得了成功，國內已有多家引進，國內外諸多學者對其進行了研究。Pecat等［7］對比了低頻振動（振幅為0.01～0.20 mm，頻率為1.5/rev）輔助鉆孔和普通鉆孔（conventional drilling，簡稱CD）。試驗發現：合理的振幅、進給速度與主軸轉速，軸向低頻振動輔助鉆孔（low frequency vibration assisted drilling，簡稱LFVAD）不僅可以有效斷屑，同時還可將鈦合金鉆孔溫度降低40%以上，使CFRP/Ti疊層板的孔質量有了顯著的提高。文獻［8-9］將其刀具振動曲線假設為完全正弦曲線，對低頻輔助鉆削過程的幾何斷屑［10］機理做了一定的解釋。Bisu等［11］提出一種計算振動鉆削設備特性的試驗方法，從而有效預測最佳鉆削參數，并對振動鉆孔過程的沖擊動力學進行了分析。

在前期研究中，本課題組研發了高低頻復合振動鉆孔樣機，對普通、旋轉超聲和低頻振動等3種方式鉆削疊層板的對比分析發現：超聲鉆削雖能降低軸向力，改善斷屑與排屑性能，但其在鉆削過程并不能實現完全斷屑，更多的是降低切屑的強度而獲得的機械斷屑。低頻振動輔助鉆孔機構在斷屑、鉆孔溫度和鉆孔質量等方面有明顯優勢［12］，因此低頻振動鉆削或許是更好的發展路徑。但是在研究中也發現低頻振動鉆孔過程中存在有明顯的非線性動力學特性。非線性的主要來源是在振動鉆削過程中軸向切削力的非線性。Chang等［13］提出了一種新的預測6061-T6鋁振動鉆削時的軸向切削力模型，在4 kHz～12 kHz的范圍內發現預測值與試驗值的誤差由改進前的20%下降到7%。

在非線性共振的利用方面，文獻［14-16］都進行了很好的工作，發展了非線性共振篩的理論，做出了很好的技術產品，為非線性共振的利用提供了思路。

本研究將在動力學試驗的基礎上，首先進行動力學建模與試驗參數估計，然后進行非線性振動分析，并試圖解決振動鉆孔系統的穩定性與振動利用的問題。

1 振動鉆孔系統的動力學試驗

振動鉆孔過程是一個動力學特性十分突出的過程。為了實現穩定的鉆孔作業，必須對其動力學特性進行先期研究，為此先搭建了試驗臺并對其動力學特性進行了試驗。

1.1 振動鉆孔試驗臺

試驗設備為自主研制的低頻振動輔助鉆孔設備，如圖1所示。該設備主軸轉速可調，最高為3 000 r/min；激振力頻率和幅值可調，最高頻率約為50 Hz；可以實現軸向力與軸向進給的實時監控與反饋。

圖1 振動鉆孔試驗臺Fig.1 Equipment of vibration assisted drilling

1.2 動力學測試分析系統

試驗所用測量系統如圖2所示。主要包括：KISTLER 9129A測力系統，用于測量鉆削過程的鉆削力與扭矩；Polytec非接觸單點式激光測振系統，進行鉆頭位移信號的測試；LMS振動測試分析系統，用于振動加速度信號的測試分析。

圖2 試驗測量系統示意圖Fig.2 The schematic diagram of test measurement system

1.3 振動鉆孔系統動力學試驗參數

為了研究該系統的動力學特性，在空載條件和表1所示的參數下，通過改變激振頻率，進行了正向（20→50 Hz）和反向（50→35 Hz）掃頻試驗。在該試驗過程中工件材料為Ti6Al4V，其主要性能參數如表2所示。

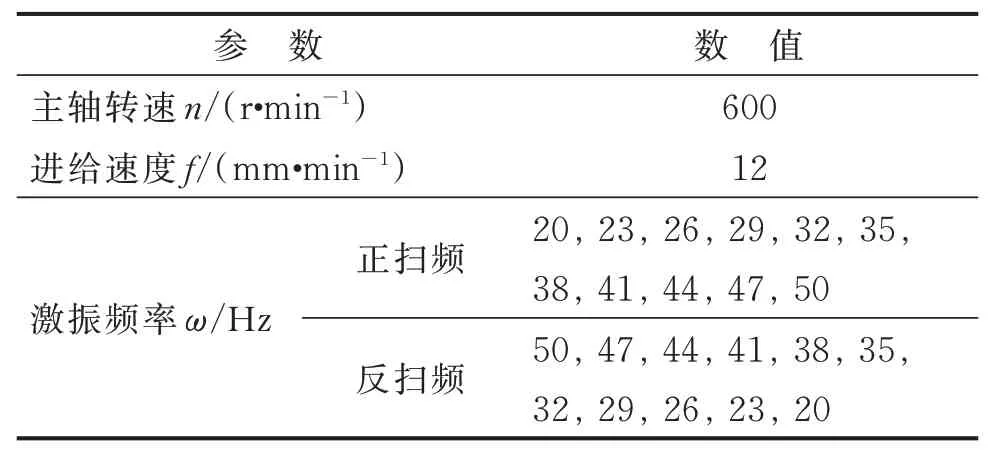
表1 掃頻試驗參數表Tab.1 Parameters of swept frequency test

表2 鈦合金主要性能參數Tab.2 Major properties of titanium alloy

1.4 振動鉆孔系統的動力學試驗分析

為了研究切削過程對于系統的特性的影響，本研究通過采集振動鉆的加速度信號來反映整個振動鉆的軸向振動狀態。圖3（a）和（b）分別展示了系統在激振頻率為35 Hz、激振力幅值為180 N條件下，分別在空載與切削狀態下運行時加速度信號（縱坐標物理量綱為重力加速度g）的時域與頻域特征對比。

由圖3（a）中看出，當系統空載運行時，鉆頭不與工件發生接觸，系統的時域與頻域特征表明系統此時主要以線性振動特征為主。雖然在35 Hz的主頻成分之外也存在的3倍頻和5倍頻成分，應該是由相對運動件之間的滾動摩擦引發，幅值很小可以忽略。

一旦系統進入鉆削狀態，則由圖3（b）可以發現，除了主頻成分外還會出現一定幅值的倍頻成分，特別是3倍頻幅值較大。從振動切削的過程來看，鉆頭除了自身勻速旋轉外，又在進給方向施加了簡諧激振力，致使切削厚度周期變化并形成斷屑。此時鉆頭與工件之間的切削力具有了非光滑的特質。這樣的反作用力施加于振動系統使其具有了非光滑和非線性的特征。

圖3 振動加速度的時域與頻域特征Fig.3 Characteristics of vibration acceleration in Timedomain and Frequency-domain

為進一步研究系統的非線性特征，進行了掃頻試驗，得到了圖4所示的幅頻特性曲線。從圖4可以看出：①空載情況下，該系統具有明顯的偏心激勵下的單自由度線性振動系統的特征，固有頻率為25 Hz，共振幅值為0.28 mm；②當系統進入鉆削狀態后，通過正向與反向掃頻試驗發現系統存在滯后和跳躍等非線性現象，說明系統具有了硬特性彈簧力非線性特性［14］，初步分析認為這是由于鉆頭相對于工件發生軸向振動情況下，鉆頭與工件發生斜碰撞切削運動導致系統的彈性力出現了顯著的分段非線性特征；③共振區的振動位移幅值由空載時的0.28 mm下降到振動鉆孔時的0.13 mm，說明系統的切削過程耗能強烈，致使系統具有了較強的阻尼特性。考慮到切削過程的非線性，此阻尼力也應具有非線性特征。

圖4 振動鉆孔系統的幅頻特性曲線Fig.4 Amplitude frequency characteristic curve of vibration drilling system

顯然，從理論上進一步搞清楚該系統的非線性特性與規律，無論是對于設計優化振動鉆孔系統，還是進行鉆孔過程的動力學與工藝參數優化都具有重要意義。

圖5 研究策略示意圖Fig.5 Schematic diagram of research strategy

筆者對該類強耦合非線動力學系統的研究策略如圖5所示。首先，對振動切削過程給系統帶來的非線性力進行等效化處理，獲得振動系統的非線性力的表達式與參數，從而對其動力學特性進行定性研究并找到系統的穩定工作參數域；其次，在此動力學參數下初步研究影響該類材料鉆孔質量的振動斷屑問題。

2 振動鉆孔過程建模與參數估計

進行非線性動力學分析的前提就是要確定系統的基本模型并通過試驗測試分析，進行動力學參數估計。考慮到本系統存在的固有頻率增大和共振振幅顯著減小的特點，擬先采用分段線性的剛度與比例阻尼來把切削過程的非線性力等效化。

理想化后的物理模型如圖6所示。圖中：m1為振動體質量；m0為慣性塊質量；C1為空載狀態阻尼系數；K1為空載狀態剛度系數；K2為鉆削附加剛度系數；C2為鉆削附加阻尼系數；δ為平衡位置與切屑表面距離；r為慣性塊驅動半徑；ν為慣性塊角速度；x為m的 位 移。

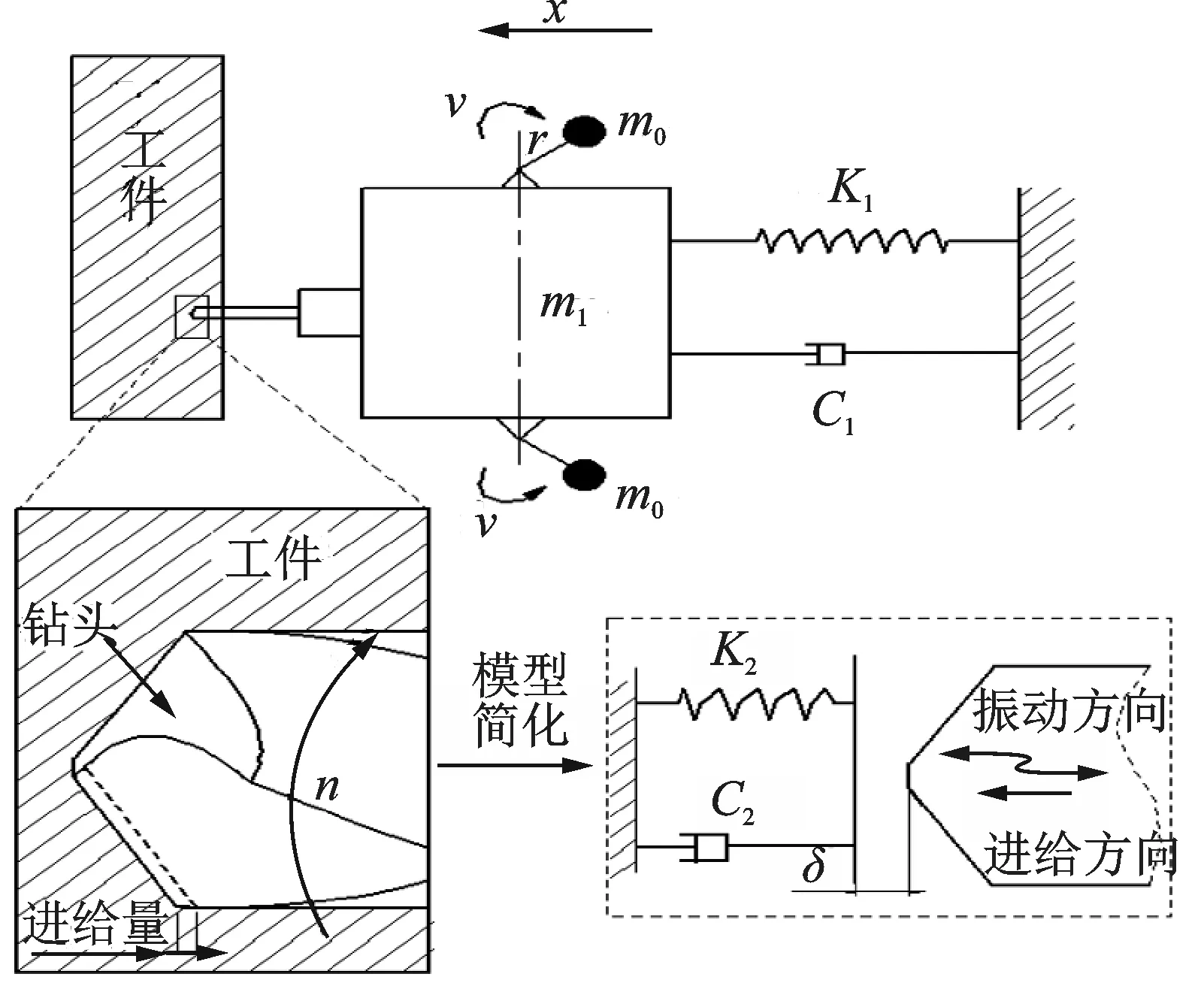
圖6 振動鉆孔系統的理想化模型Fig.6 The idealized model of vibration drilling system

根據圖6以鉆尖所在平衡位置為零點，設進給方向為正，建立坐標系。系統在振動鉆削過程中，鉆頭與工件接觸前后的振動微分方程分別為

其 中：C=C1+C2；K=K1+K2；m=m1+2m0；P1=mrν2；C為 鉆 削 狀 態 阻 尼 系 數；K為 鉆 削 狀 態 剛 度系數。

在空載狀態下，線性系統的動力學參數為：系統剛度K1=4×105N/m；阻尼系數C1=1 000 kg·s/m。

現在的主要問題就是如何對切削過程中的等效剛度與等效阻尼進行參數估計。為此將振動系統在一個周期內所測得的位移、加速度和軸向力進行了對比分析。

圖7 為激振頻率35 Hz時加速度-位移-軸向切削力在同一時間坐標下的時間歷程對照圖，時間長度為0.05 s。通過比對鉆頭的振動加速度、位移以及軸向切削力，可以確定從t1～t7為一個切削周期，其中從t2～t4為刀刃進入切削區的過程即切削過程。在鉆尖向下運動過程中，一旦接觸到工件表面，就會引起系統加速度與軸向切削力出現極值或者折點，如圖中t2時刻；而后進入切削狀態，直至鉆尖脫離切削區，再次引發振動加速度與軸向切削力的突變，如圖中t6時刻。

圖7 單個振動周期內的動力學信號對照Fig.7 Comparison of dynamic signals within a single vibration period

通過觀察多個周期，得到在切削過程中的平均鉆削力Fd≈500 N，平均切削距離L≈0.1 mm，平衡位置與切削表面距離δ≈0.05 mm，振幅B=0.1 mm。

根據阻尼理論［17］

其中：W為鉆削過程所做的功；a為常數；ω為激振頻率；P為鉆削狀態固有頻率。

3 振動鉆孔系統的非線性平均法分析

由于該系統是在近共振狀態下工作的，所以為了便于進行非線性分析，采用共振情況的平均法進行分析。將式（1）中的兩式合并，并在非線性彈性力部分、阻尼和干擾力前標以小參數ε后，其控制方程變為

圖8 非線性彈性力示意圖Fig.8 Diagram of nonlinear elastic forces

圖9 阻尼示意圖Fig.9 Damping diagram

應用平均法［15］得出系統的穩態幅頻響應方程

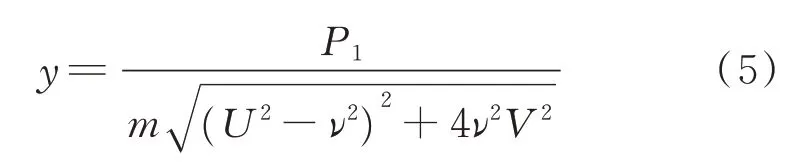
其中

其中：φ0=sin-1(δ/y)。

由式（5）知，它和線性系統強迫振動的解的表達式形式上完全相同，U和V都是振幅y的函數。將v解出

其中：λ=m0r/my。

代入系統相應參數，由式（8）可畫出一組參數的y?v曲線——幅頻特性曲線（如圖10所示），A?B?C為振動頻率正向增加時的穩定工作區域，C?D為不穩定工作區域，不可實現，而D?E為振動系統從高頻降速時的穩定工作曲線。顯然本系統應該選擇在B?C區域并靠近C點的區域工作。在該區域不僅振幅較大而且當外界條件變化時，振幅變化較小，設備運行更加平穩。

圖10 幅頻特性曲線Fig.10 Amplitude-frequency curve

4 鈦合金振動鉆孔試驗

4.1 鈦合金板振動鉆孔的試驗方案設計

以主軸轉速為n和進給速度f進行鈦合金工件鉆削試驗。試驗激振頻率為35 Hz，分別進行普通鉆削與振動鉆削。低頻振動激振裝置在加工前開啟，等待振動穩定后再進行鉆孔過程，具體參數見表3。試驗重復4次，每組試驗結束更換鉆頭，獲得平均值與誤差分布。

表3 鉆削試驗參數表Tab.3 Drilling test parameters

4.2 振動鉆孔過程試驗

切削中的切削力是切削效率的直接反映。而對于鉆孔而言，鉆孔的軸向力的大小不僅能反映鉆孔的切削效率，更能直接反映斷屑效果和鉆孔質量。尤其是對于鈦合金這類強度高、塑性強、導熱率低的航空材料板材，鉆孔過程的中軸向力更是重要的控制指標。

鉆孔過程一般分為：鉆入階段、中間穩定鉆削階段和鉆出階段等3個階段。文中通過采集所加工的工件所承受的軸向力來反應鉆削過程的切削力，如圖11（a）（b）分別為普通鉆削和低頻振動鉆削時，軸向力隨時間變化的時間歷程。圖12為中間穩定鉆削階段的軸向切削力平均值的對比。

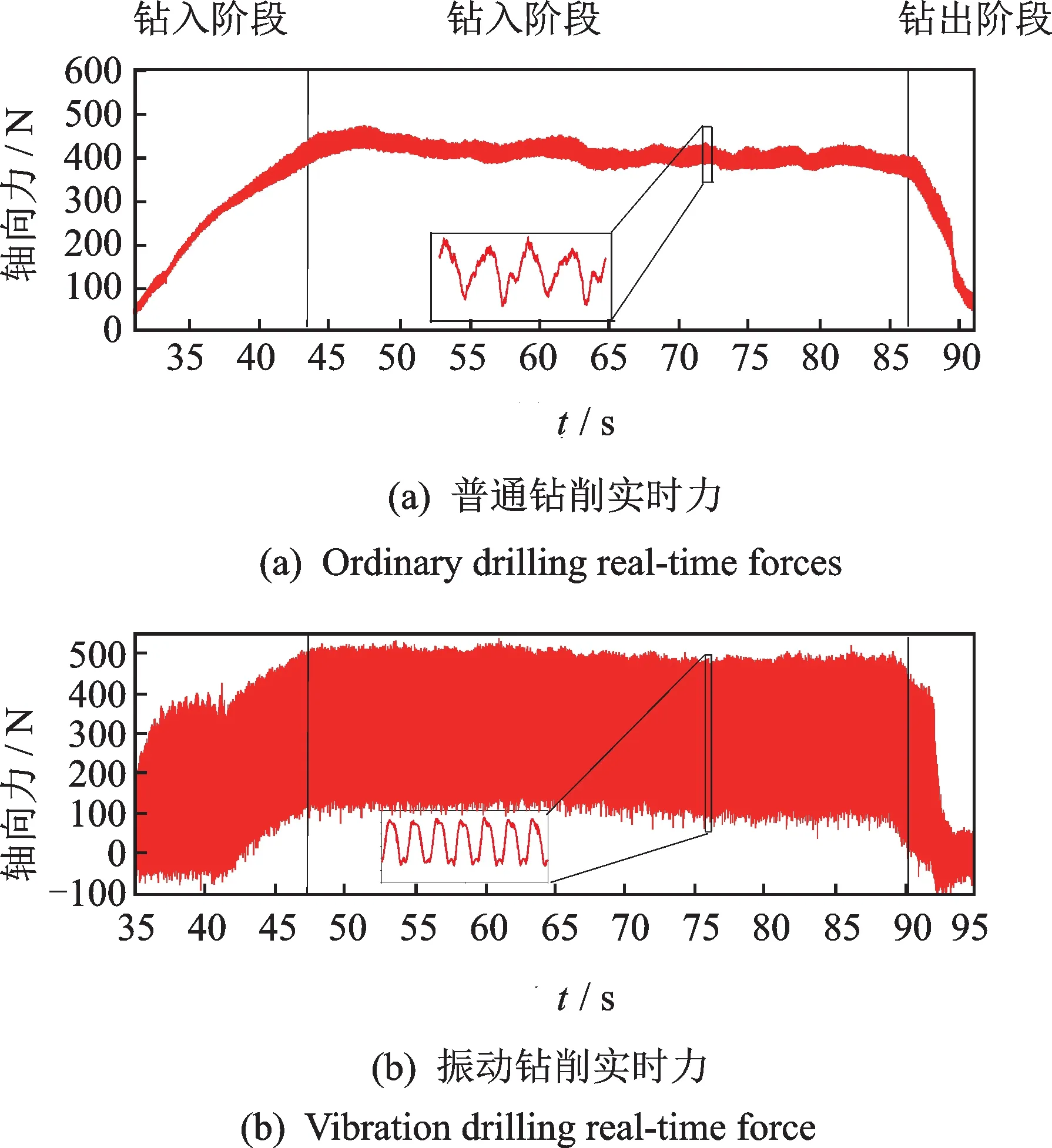
圖11 軸向力隨時間變化Fig.11 Thrust force changes with time

圖12 普通鉆削與振動鉆削平均軸向鉆削力Fig.12 The mean value of CD and LFVAD

圖13 為普通鉆孔與振動鉆孔的切屑情況對比。鈦合金的韌性高，鉆削過程易出現連續切屑，影響制孔質量，因此鉆削過程斷屑至關重要。普通鉆削過程中排出的鈦合金切屑為螺旋狀連續切屑，如圖13（a）所示；在低頻振動引入后，原來的螺旋長屑被切斷為獨立的扇形，如圖13（b）所示。

圖13 鈦合金切屑形態Fig.13 The chip morphology of Ti6AlV

由此可以看出：普通鉆削狀態下切屑為螺旋形連續長屑，而軸向力幅值的波動較小，平均值較大且平均力在每次鉆孔過程中出現較大幅度的離散性；反觀引入軸向振動后，不僅切屑由螺旋長屑變成了斷屑，其軸向切削力雖然因為碰撞的發生而使得其最大值增大，但平均值卻顯著降低而且更加平穩。這說明低頻振動的引入提高了鉆頭的切削能力同時實現可靠斷屑從而改善排屑，使得鉆削過程更加穩定。

5 結束語

筆者搭建了振動鉆孔試驗臺，通過對鈦合金的振動鉆孔動力學試驗發現，該系統存在明顯的硬彈簧特性的非線性振動特征，會出現滯后與跳躍等非線性動力學現象。通過動力學建模與試驗參數估計，獲得了本試驗臺的關鍵動力學參數，建立了該系統的動力學模型。對該動力學模型進行了近共振情況下的平均分析，獲得的幅頻特性曲線與實測結果定性一致，為后續的深入研究奠定了基礎。利用該系統在所選定的振動與工藝參數下對鈦合金進行了鉆孔試驗說明：通過恰當的動力學設計，巧妙利用切削過程的非線性可以使振動鉆孔過程更平穩、功耗更低而且孔質量更好。