基于FPGA的神經網絡算法應用研究

劉維華

(中共陜西省委黨校陜西行政學院 文化與科技教研部， 陜西 西安 710000)

0 引言

視覺神經網絡算法的基本原理是以收集圖像數據為基礎,對外界圖像進行處理，并通過GPRS無線系統將圖像的信息單元以沖脈電流方式對神經網絡組織進行適當的感官接觸，起到視覺神經興奮的作用，在一定的電流刺激過程中可以使人的視覺感官對眼前的事物有基本的識別能力[1-2]。盡管國內外研究學者在視覺網絡辨別中取了很多的研究成果，但是受到信號交互、電極硬件設備和結構部件通訊等技術因素制約，可以實現視覺感官刺激的電流模塊非常少。本研究以DretionNet模型和ReaqiueNet模型為基礎，通過神經網絡算法進行優化，得到基于FPGA的高效算法的神經網絡模型，對其多條分支的組織結構進行優化[3-5]。根據DretionNet模型和ReaqiueNet模型的評價分析，得到兩種模型針對神經網絡算法的改進點，并以設備性能提升為依據，結合神經網絡適應的優化設備，對原有的神經網絡模型進行改進，根據優化后的神經網路模型和FPGA為基礎的高速網絡算法，提出多分支的深度卷積算法，根據設備中的卷積算法,運用電流脈沖和數據采集系統，更好地提升算法效率。

1 神經網絡模型

1.1 DretionNet模型

DretionNet模型相對于其他模型有更好地兼容性和可塑性，由于DretionNet模型是根據原有模型的基礎改良而成，因此其參數和結構是可以結合實際情況進行改變[6]。針對模型的不同敏感參數，結合參數的變化程度可以隨時調整，這樣類似的改變可以有效控制研究模型被修改，導致因參數變化引起模型精準度降低的結果，此類模型特征改變在視覺神經網絡算法中起到非常重要的作用[7-8]。在實際工作過程中，由于工程應用需要滿足圖像清晰度、像素種類識別和工程中的精準度要求，對原有的視覺神經網絡按照劃定的規格進行校對。DretionNet模型不僅滿足模型修改過程中的兼容性，而且可以使開發者獲得視覺神經網絡的對應模型，DretionNet模型是可以改變的，提高了模型的構建效率和開發模式，根據DretionNet模型原始參數標準，模型參數結構,如表1所示。

1.2 ReaqiueNet模型

ReaqiueNet模型的主要架構是以視覺神經網絡局部算法的最優解決方式進行卷積網絡的模型結構實現，如圖1所示。

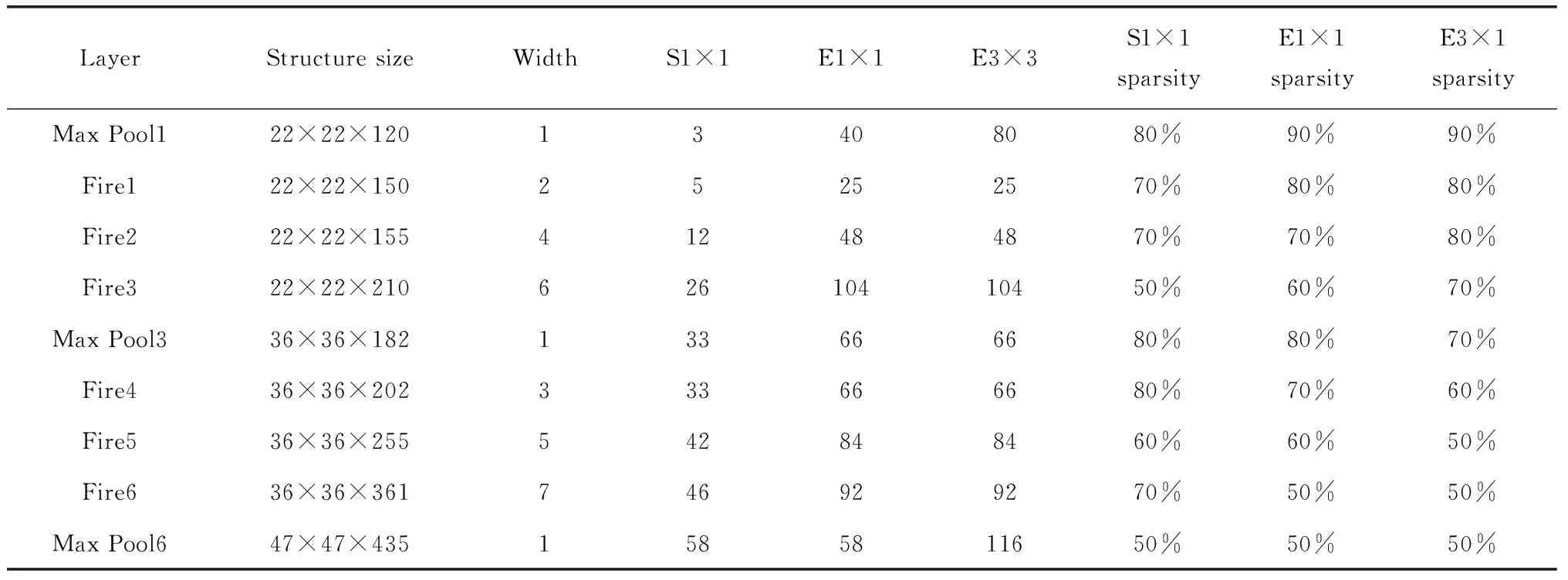
表1 DretionNet模型參數

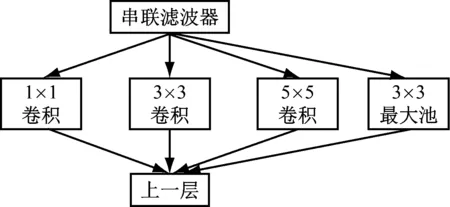
圖1 ReaqiueNet結構

根據ReaqiueNet模型的疊加效果，其結構模型在輸出結果方面一定會發生變化，在結構優化方面，模型的最高層會捕捉其形態特征，但模型的空間密集度會降低，這意味著指標層會轉移到較高層次，視覺神經系統中的其他層次結構隨之增加[9-10]。ReaqiueNet模型在Cliet V1、Cliet V2結構中可以繼續使用等比例層次的卷積模式，盡管在模型構建過程中可以為結構層次進行替換，但ReaqiueNet模型在其他多分支結構數量中的比例沒有發生變化，仍然可以保持已形成的模型數量。

2 基于FPGA視覺神經網絡

2.1 網絡模型多層次分支

DretionNet模型和ReaqiueNet模型在視覺神經網絡計算過程中可以降低模型參數的使用量和運算過程，緩解了建模壓力，從而有效提高了FPGA在大數據平臺的計算能力。但是此類算法在模型構建的過程中顯示出不完全的適應性，導致網絡模型在工程實際過程中運算效率被降低，實驗結果因此會受到影響，無法滿足在實際應用中的計算步驟。結合中外學者的研究成果，以基礎模型構建為基礎，總結在不同網絡模型中的計算缺陷，研究基于FPGA神經網絡的多分支同步算法。

由于構建的參數模型對計算機硬件平臺的運算條件具有很高的要求，根據DretionNet模型和ReaqiueNet模型的構建機理，以改善計算機硬件平臺為出發點，結合模型多分支結構分布特點，通過對DretionNet模型和ReaqiueNet模型多層次分支結構的數據進行分布統計，并根據數據統計結果重新分流調整，確保計算精度的前提下，減緩各個分支計算路徑的延遲效果。在分散的結構模型中，通過減少卷積模型數據通道的輸入量，降低后期模型構建過程中運算量激增的問題，可以較好地提升計算機的硬件平臺的運算效率，并降低了數據導入時間。設定第i層的圖像輸入量為ci×si×zi，按照卷積模型從上至下的運算順序，則DretionNet模型和ReaqiueNet模型的參數計算量,如式(1)。

ei=ci×si×zi

(1)

若降低卷積模型的運算維度，提高數據模型的計算精度，則模型的計算參數,如式(2)。

ei,s+ei,e=ci×m+m×si×zi

(2)

式中，模型參數m不應大于公式中的其他單元參量，這樣可以保證構建模型在運算過程中降低參數的數量，減少模型的體量，提升參數的運算效率。

2.2 基于FPGA結構折疊

基于FPGA神經網絡的深度卷積算法中，采用深度卷積分割法對構建的模型進行分步計算，對照構建的標準模型，將一個深度卷積算法分割為1×1，3×3，5×5……(2n-1)×(2n-1)單層次的模型分量，運用FPGA將獨立的卷積模量插入在每個模型的運算通道上，并按照單一的卷積模量進行重新輸出，一個合理的卷積模型不僅可以滿足數據的輸入，還可以在新的計算過程中輸出一組新的組合計算量。FPGA在深度卷積計算過程中可以把構建的模型分割為兩個部分，其中一部分是將通道數據進行卷積量化，另一部分將量化的數據重新組合。

標準卷積模型參數量化并重新輸出的計算方式,如式(3)。

Gi,s,n=∑i,j,mKi,j,m,n×Fi+j-1

(3)

深度卷積在模型分割為單層次結構進行重新輸出的計算,如式(4)。

P=Fn×M×N×K×Di×Dj

(4)

按照標準模型卷積項M×N×K產生的特征值G，并重新輸出產生GM×GN×GK的特征圖，圖像的特征寬度和高度滿足深度卷積的計算要求，M是數據輸入通道的容積量，N是數據輸出通道的容積量，D是特征圖像的尺寸大小。

3 結果分析

按照深度卷積模型的計算標準，基于FPGA的多分支同步算法的輸出結果呈現出對稱性且互不干擾，根據DretionNet模型和ReaqiueNet模型的層次結構，從模型的頂端到底部呈現相互疊加的形式，模型后一層的容積量是前一層容積量的2倍。ReaqiueNet模型運用了常見的5×5結構尺寸，并以兩個結構單元為標準作為深度卷積模型的滑動窗口，構建模型的過程中采用了結構交叉方案，因此對模型邊緣的數值做歸一化處理不會影響結構尺寸。改良后的結構尺寸,如表2所示。

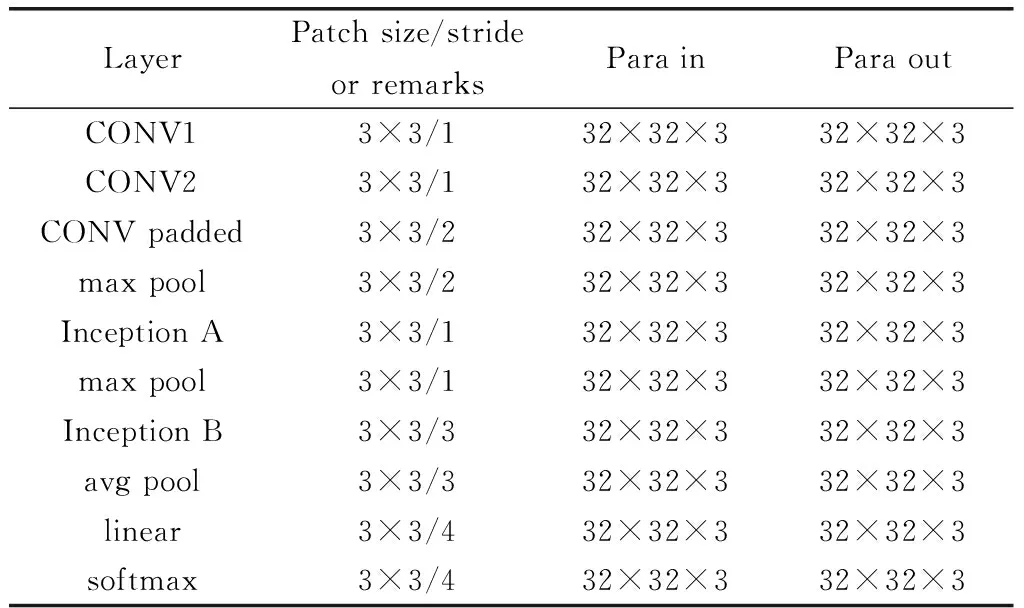
表2 改良的Inception體系結構尺寸

在5條支路模型的輸入量為13×13×3，深度卷積核的數量為46組，以FPGA作為ReaqiueNet模型的優化標準，運算結束后5條支路的輸出量為5×5×3，深度卷積核的數量保持不變。

DretionNet模型和ReaqiueNet模型的準確率隨著修改次數的改變而變化，如圖2所示。

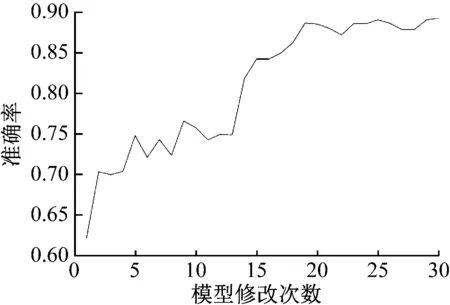
圖2 模型修改次數與準確率比較

當修改次數低于3，模型的準確率會有較大幅度的提升，當修改次數介于3和14之間時，模型準確率在70%至75%之間震蕩，修改次數大于15時，模型準確率增長速率較快，最高值可達90%。模型深度卷積次數由5×5轉換為5×1/1×5，不僅提高了運算速率的準確性，而且可以保證模型結構的完整性。

不同網絡模型的誤差率也存在差異，構建模型不同誤差率的區別,如表3所示。

表3 不同模型數據準確率比較

由表3中統計數據可以看出，DEP模型的誤差率為13.69%，MIN模型的誤差率為10.41%，改良前模型平均誤差率為11.78%，基于FPGA改良模型的誤差率僅為6.06%，模型誤差率顯著下降，但改良后的模型與深度卷積模型的結構樣式保持不變。

4 總結

本研究針對DretionNet模型和ReaqiueNet模型的優化改進，結合傳統模型的在一般硬件設備中存在的問題，提出以FPGA為基礎的高效網絡模型算法，運用FPGA將獨立的卷積模量插入在每個模型的運算通道上，并按照單一的卷積模量進行重新輸出，當修改次數介于4與13之間時，模型的準確率會有較大幅度的提升，以FPGA為硬件改良模型的誤差率僅為6.06%，顯著提高了神經網絡算法的識別精準度。