組合梁抗彎極限承載力參數影響分析*
代 力 江祥林 朱澤文 何雄君
(1.江西省交通科學研究院 南昌 330200; 2.長大橋梁建設關鍵技術及裝備交通運輸行業研發中心 南昌 330200;3.武漢理工大學交通學院 武漢 430063)
鋼-混組合結構是在鋼結構與鋼筋混凝土結構上發展而來的新型結構,這種組合結構具備承載力高、剛度大、截面尺寸小,以及施工快速等優點,近幾十年來,鋼-混組合結構的發展速度很快,實踐證明鋼-混組合結構能較好地滿足現代結構的功能需求[1],而抗彎極限承載力作為組合梁重要的承載技術指標值得深入研究。
Kemp[2]對采用工字型鋼梁的組合梁進行了試驗研究,探究組合梁在彎曲情形下的穩定性能,分析組合梁失穩破壞時的受彎承載力和變形能力。結果表明,鋼梁腹板高度、翼緣厚度、腹板厚度及翼緣寬度等參數對組合梁抗彎承載力存在較大的影響。馬增[3]利用試驗研究集簇式栓釘剪力連接程度對組合梁結構極限承載力、破壞形式及劈裂效應的影響。結果表明,集簇式栓釘的剪力連接程度對組合梁極限承載力影響較小。聶建國[4]也研究了相關影響因素對組合梁抗彎極限承載力的影響,近些年來,越來越多的學者關注組合梁抗彎極限承載力的優化措施,本文基于此,開展組合梁抗彎極限承載力參數影響分析。
1 有限元模型
為準確模擬結構的非線性行為,本文利用ABAQUS進行組合梁受彎過程的非線性模擬。
1.1 材料參數
1) 混凝土本構。單軸應力-應變關系式的上升段采用GB 50010-2010 《混凝土結構設計規范》中公式[5],下降段采用Hongnestad的處理方法,對應計算公式如下。
當εc≤εo時
(1)
當εo<εc≤εcu時
(2)
式中:σc為混凝土的壓應變為εc時的壓應力;fc為混凝土的抗壓強度設計值;εo為當壓應力達到fc時,混凝土對應的壓應變;εcu為極限壓應變,取值為0.003 3。
2) 鋼材本構。鋼材的本構模型包括理想彈塑性模型、雙折線模型,以及完整曲線模型,本構模型見圖1。
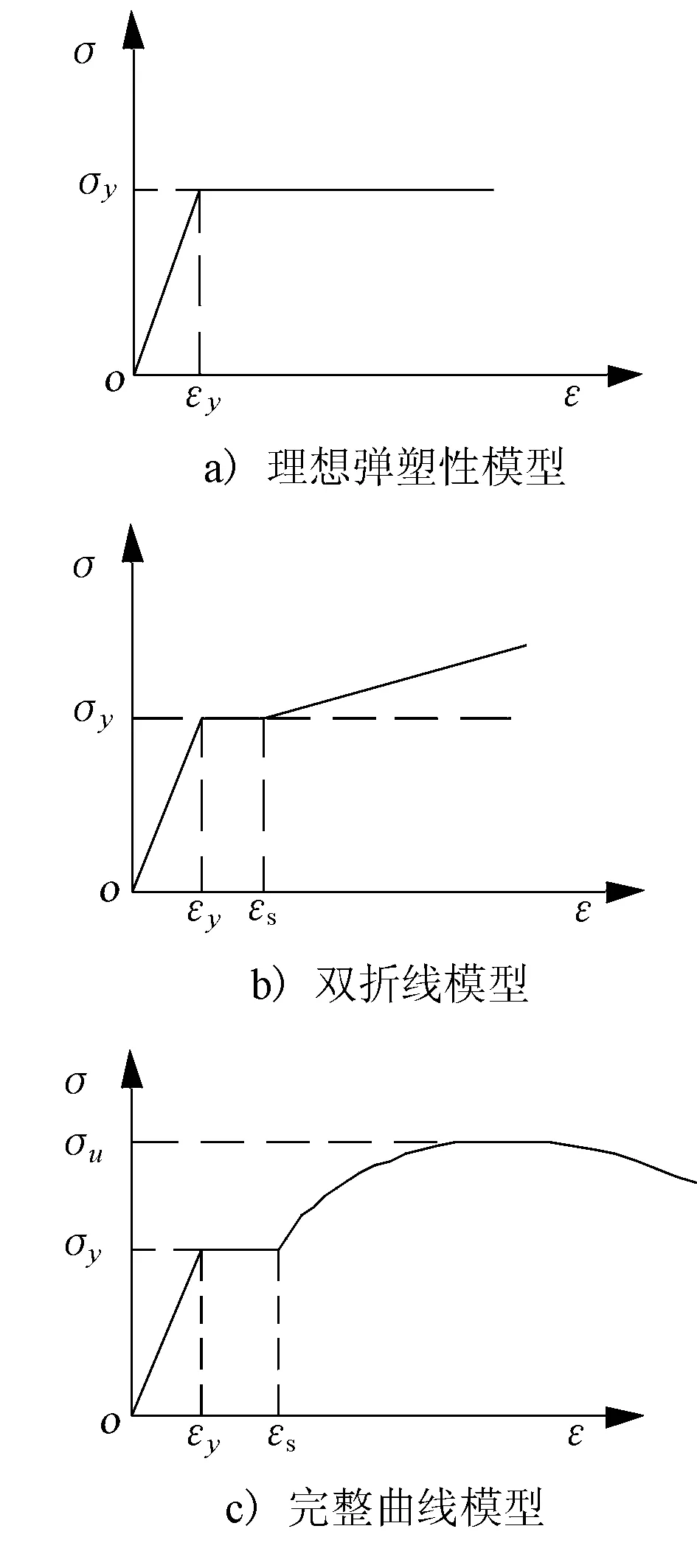
圖1 鋼材本構模型
由于理想彈塑性模型在保證計算精度時也能降低計算量,因此鋼梁本構模型取用理想彈塑性模型。其中:鋼梁彈性模量取值為2.06 GPa;泊松比取值為0.3;屈服強度取值為345 MPa。
3) 栓釘本構關系。栓釘的本構關系通常選用三折線模型[6-7],數學表達式為
(3)
式中:σs與εi分別為等效應力與應變;fsy與εsy分別為屈服強度與屈服應變;fu與εsu分別為極限強度及達到極限強度時的應變;Ess為栓釘的彈性模量,取值為206 GPa。
1.2 模型建立
在過去的組合梁結構建模中,栓釘通常選擇多自由度的彈簧進行模擬[8],本文采用精細化建模,建立栓釘的實體單元來模擬鋼梁與混凝土板的實際接觸,建模部件主要包括鋼梁、混凝土板、栓釘。各部件均采用8節點的三維實體線性減縮積分單元(C3D8R),并且注意到在模型運行中若不加入豎向加勁肋容易造成結構局部失穩,因此在支座處按實際情況添加豎向加勁肋,一般不能簡化,單元也為C3D8R實體單元。
工字鋼頂板-混凝土、栓釘-混凝土界面接觸,以及栓釘的模擬方式均影響鋼-混凝土組合梁界面滑移的大小,從而影響組合梁的整體力學性能。定義界面的面面接觸,法向采用軟件默認的“硬”接觸,切向采用罰函數接觸,摩擦系數為0.4[9];栓釘根部底面與鋼板“Tie”固結,并以“Embedded”方式嵌入頂部混凝土板,模型見圖2。

圖2 組合梁模型
2 鋼梁參數對組合梁抗彎極限承載力的影響
采用控制變量的單參數研究方法探究鋼梁強度、腹板厚度、腹板高度及翼緣板厚度對組合梁抗彎承載力的影響,組合梁截面尺寸見圖3,標準尺寸數據:bf1=bf2=400 mm,b=2 000 mm,tw=12 mm,h=180 mm,t1=t2=12 mm,h1=634 mm。
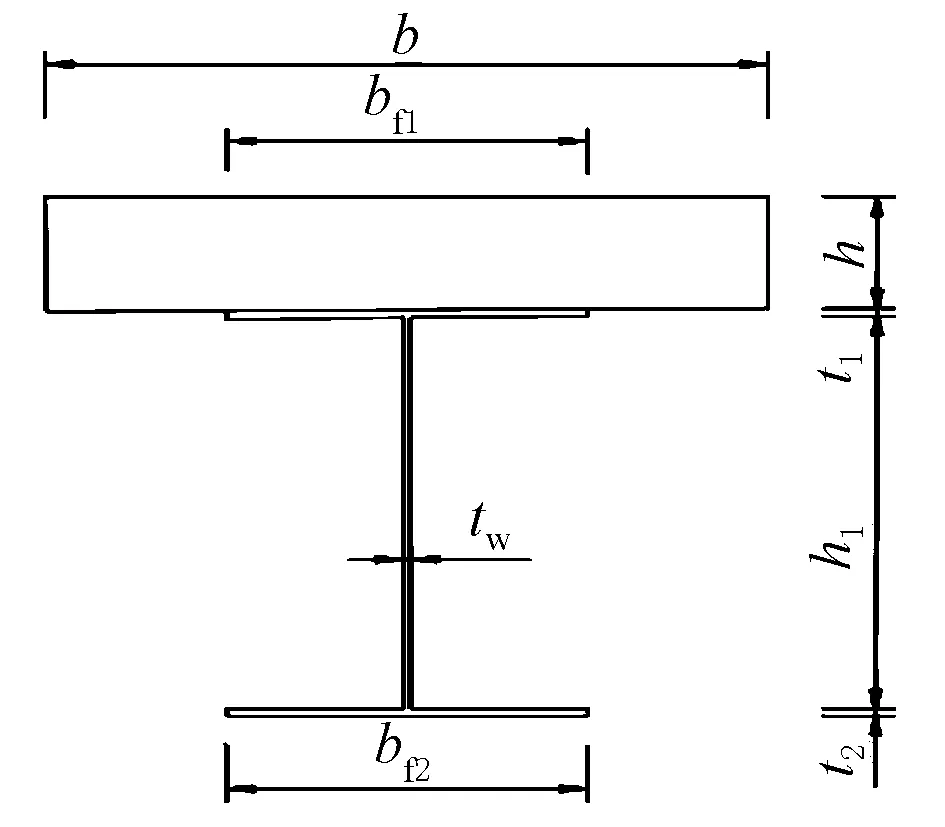
圖3 組合梁截面尺寸參數
在探究鋼梁強度對組合梁抗彎極限承載力的研究中,以鋼梁強度等級為變量,分別取強度為235,290,345,390 MPa的鋼梁進行研究。以腹板厚度tw為研究參數時,tw分別取4,8,12,16 mm;以腹板高度h1為研究參數時,h1分別取360,460,560,660 mm;以上、下翼緣厚度為研究參數時,分別取6,8,10,12 mm厚度的鋼梁進行研究。荷載-撓度曲線及極限承載力隨鋼梁參數變化數值見圖4,鋼梁各參數對抗彎極限承載力的影響折線見圖5。
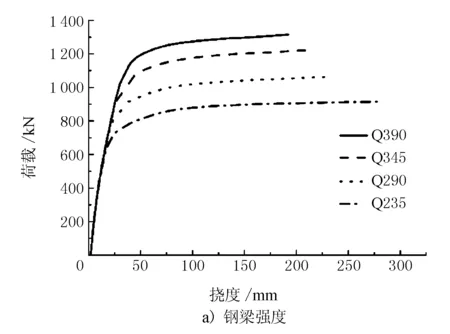
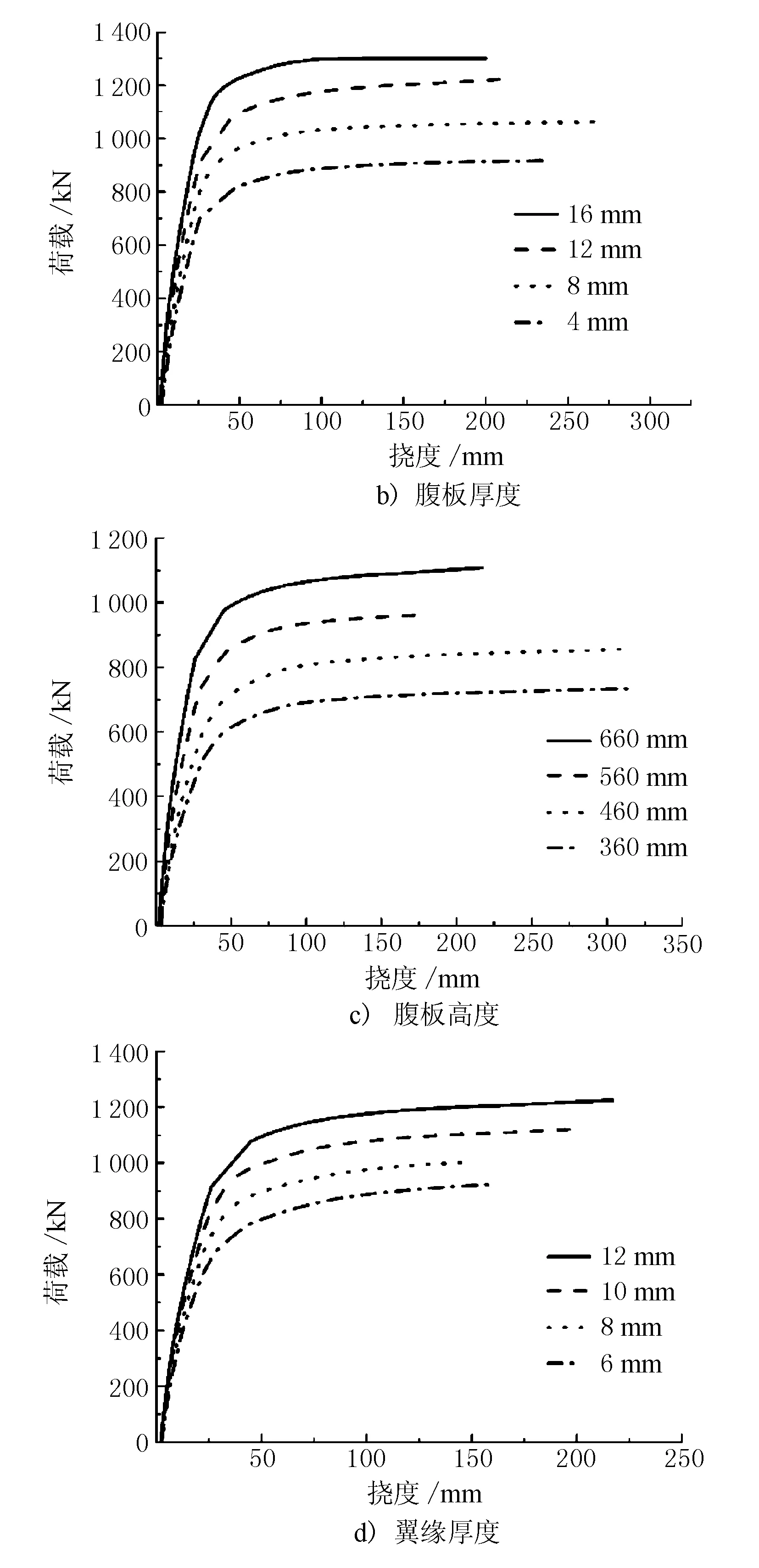
圖4 不同鋼梁參數因素下的荷載-撓度曲線
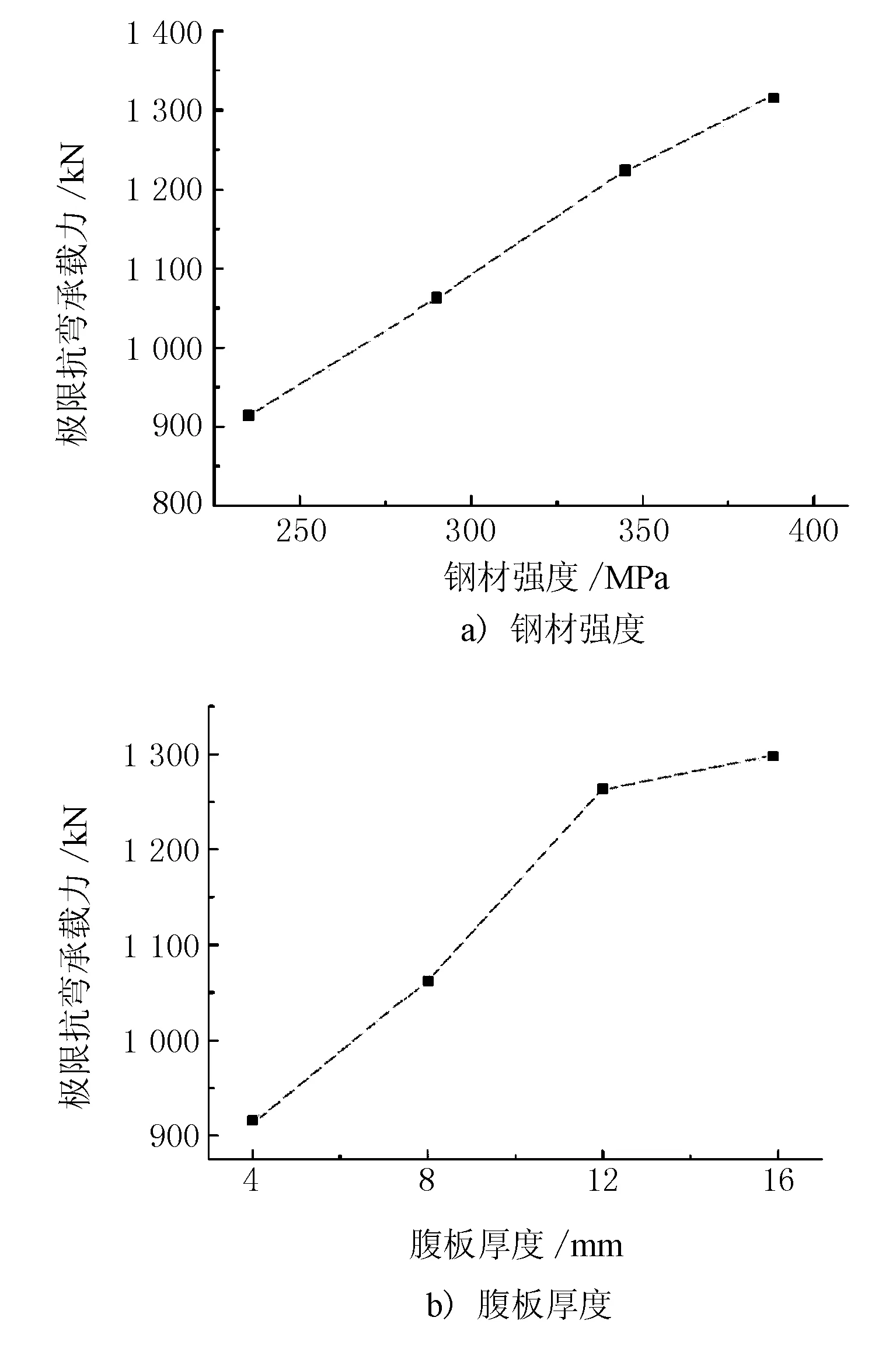
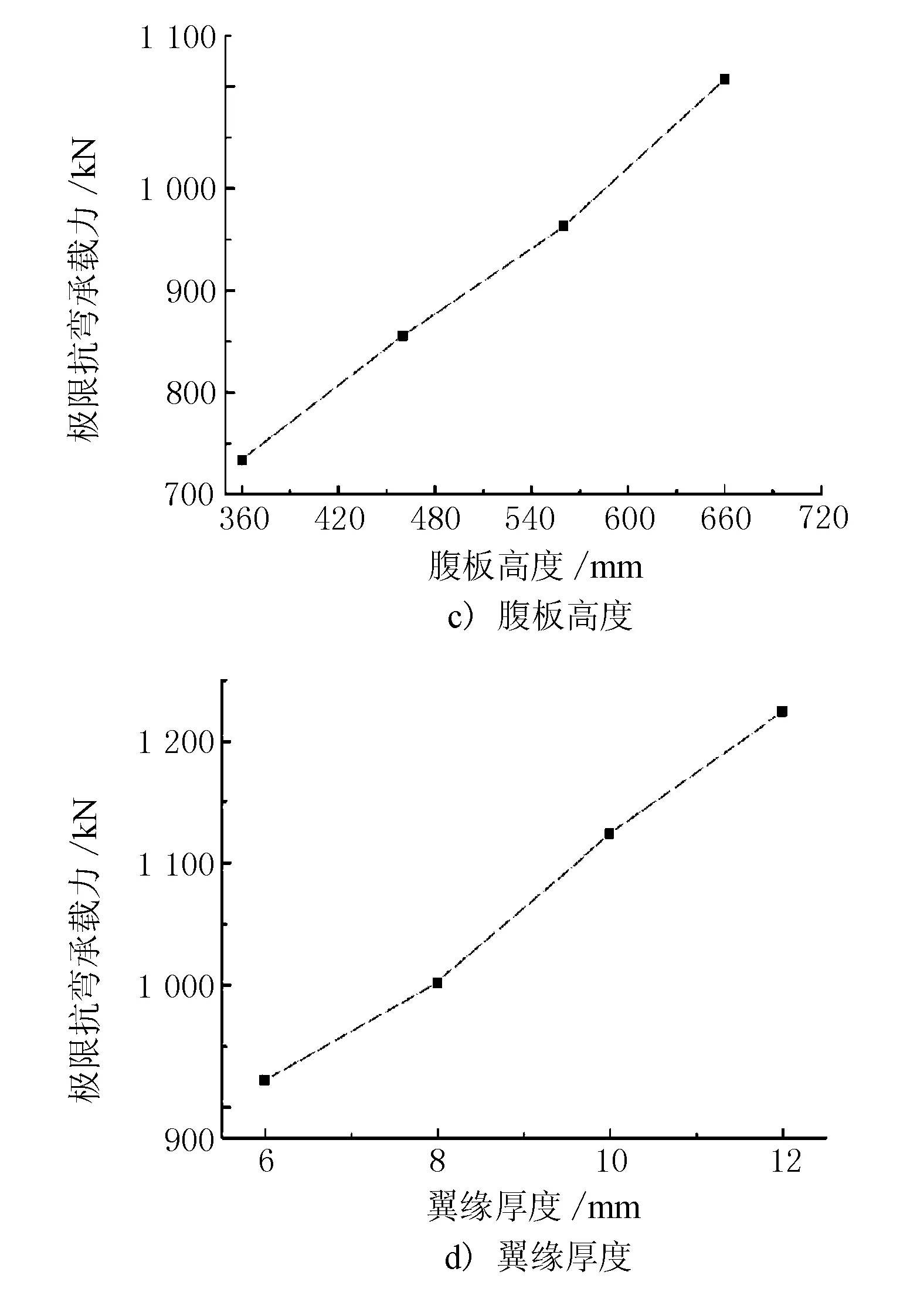
圖5 鋼梁各參數對抗彎極限承載力的影響折線
由圖4、圖5可見,上述鋼梁參數對組合梁抗彎極限承載力均有較大的影響,當鋼梁強度由235 MPa提升至390 MPa時,組合梁結構的極限抗彎承載力分別在235 MPa基礎上提升了16%,33.9%,43.7%;鋼梁腹板厚度由4 mm提升至16 mm,組合梁的極限承載力提升了40.9%,同時腹板厚度對組合梁的初期剛度也存在較大影響,在相同荷載下腹板厚度越大,撓度越小;當鋼梁高度由360 mm增加至660 mm時,組合梁抗彎承載力在高度為360 mm的基礎上分別增加了16.6%,27.5%,50.8%,同時組合梁初期剛度與鋼梁腹板高度存在較大關系,加載初期組合梁的剛度隨鋼梁高度的增加而增加;鋼梁翼緣厚度由6 mm上升至12 mm組合梁抗彎極限承載力分別在6 mm翼緣厚度組合梁的基礎上增加了8.6%,21.7%,32.6%,同時加載初期鋼梁翼緣厚度與組合梁剛度也存在聯系,提升鋼梁上下翼緣厚度有利于提高組合梁剛度。
3 混凝土板參數對組合梁抗彎極限承載力的影響
為探究混凝土強度及混凝土板板厚對組合梁抗彎承載力的影響,選取C30、C40、C50、C60混凝土及厚度為160,180,200,220 mm的混凝土板進行數值模擬分析。數值模擬所得荷載撓度曲線及極限承載力隨鋼梁參數變化見圖6、圖7。

圖6 不同混凝土強度及厚度下的組合梁荷載-撓度曲線
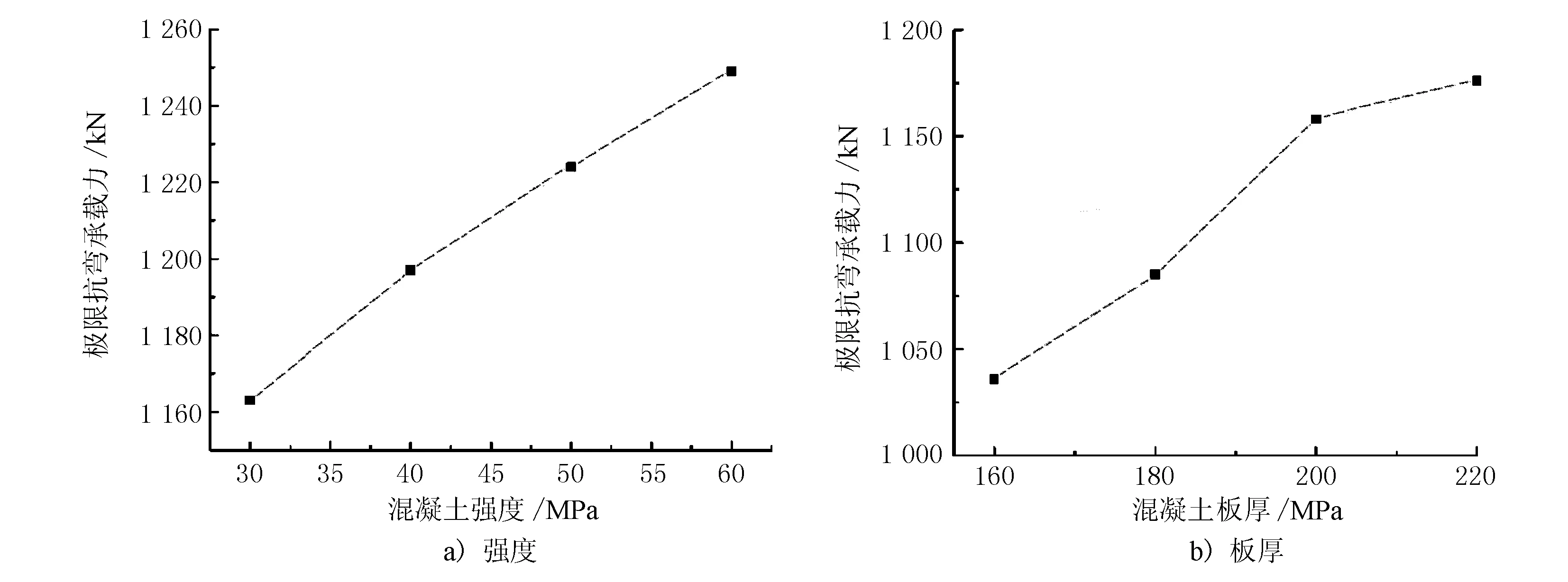
圖7 不同混凝土參數對抗彎極限承載力的影響折線
由圖6、圖7分析可知,加載初期混凝土板強度幾乎對組合梁剛度無影響。同時當混凝土強度等級由C30提升至C60時,組合梁抗彎極限承載力僅僅提升了7.4%,在所考慮范圍內混凝土強度等級對組合梁極限承載力影響不明顯,這主要是由于組合梁破壞主要由跨中截面控制,當鋼梁已經出現破壞,但是混凝土板卻未完全壓碎,混凝土自身材料性能距離破壞還有足夠的空間,即使配置再高強度等級的混凝土,由于混凝土的材料性能難以發揮,因此難以對組合梁極限承載力提升做出貢獻。
同時當混凝土板厚度由160 mm提升至220 mm時,組合梁抗彎承載力提升了20.4%,可見在工程設計中增加混凝土板厚度是提升組合梁抗彎極限承載力的有效途徑。
4 栓釘參數對組合梁抗彎極限承載力的影響
選取直徑為13,16,19,22 mm的栓釘進行數值模擬,數值模擬所得荷載撓度曲線顯示極限承載力隨鋼梁參數變化見圖8。由圖8可見,在加載初期栓釘直徑與組合梁剛度有較大關系,增大栓釘直徑有利于提升組合梁剛度。同時當栓釘直徑以3 mm為梯度由13 mm上升至22 mm的時候,組合梁的極限抗彎承載力分別在13 mm的基礎上增加了11%,23.4%,29%,由此可見在所考慮范圍內栓釘直徑可以影響組合梁的極限抗彎承載力。
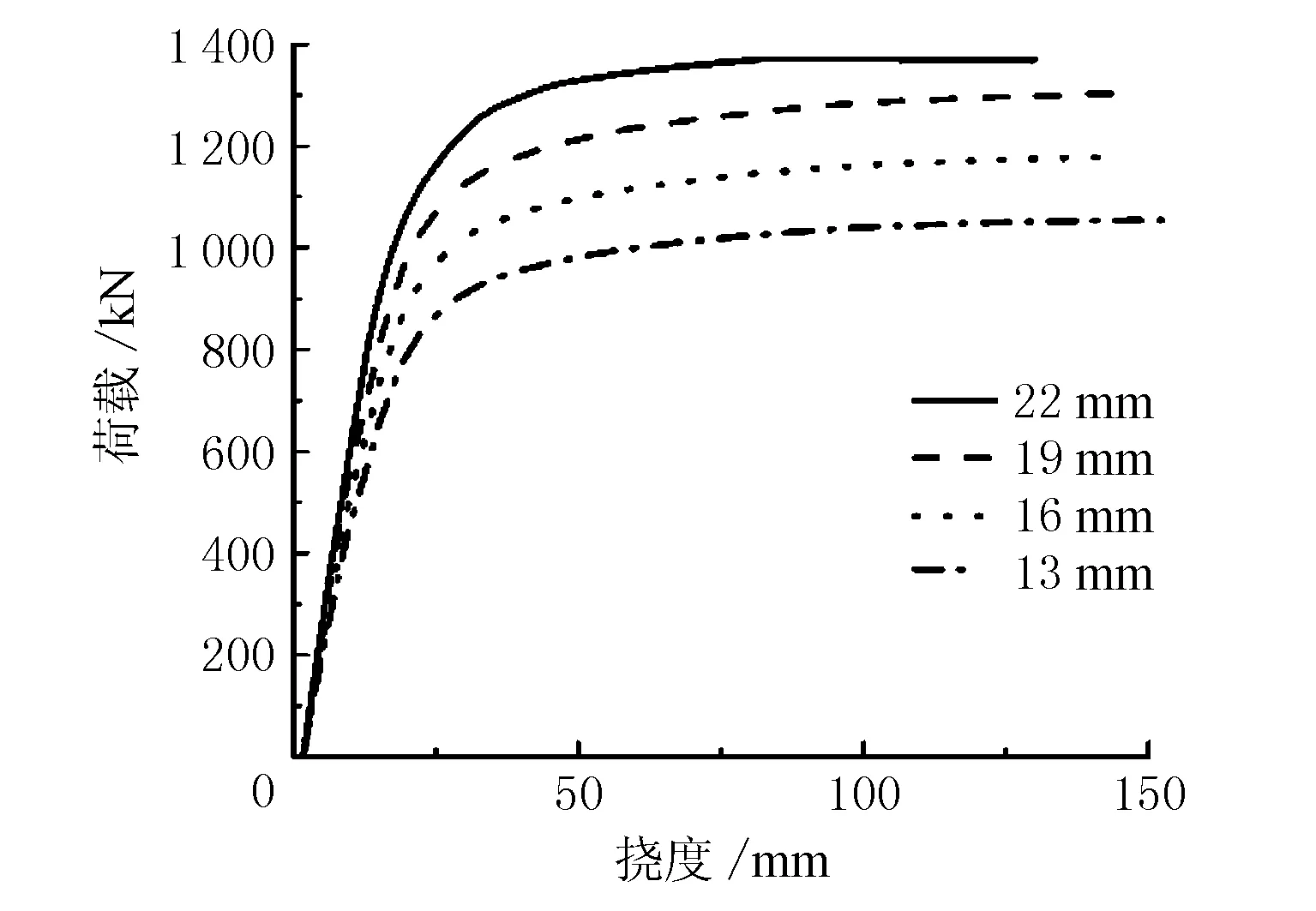
圖8 栓釘直徑影響下的組合梁荷載-撓度曲線
5 結語
本文通過ABAQUS對組合梁進行了關于極限承載力的參數影響分析,分析了鋼梁參數、混凝土橋面板參數,以及栓釘參數對組合梁承載力的影響,主要結論如下。
1) 鋼梁參數對組合梁極限抗彎承載力的影響顯著,這是由于組合梁在所考慮范圍內破壞由跨中截面控制,而跨中率先出現破壞的是鋼梁。其中鋼梁強度由235 MPa提升至390 MPa時,組合梁極限承載力提升了43.7%,鋼梁腹板厚由4 mm提升至16 mm時,組合梁極限承載力提升了40.9%,鋼梁腹板高度由360 mm提升至660 mm,組合梁極限承載力提升了50.8%,鋼梁翼緣厚度由6 mm提升至12 mm時,組合梁極限承載力提升了32.6%。由此可見,在工程實踐中,可通過提升上述鋼梁參數從而達到提升組合梁極限抗彎承載力。
2) 混凝土橋面板參數對組合梁極限承載力的影響沒有鋼梁參數顯著,當混凝土強度等級由C30提升至C70時,組合梁極限承載力提升了7.3%,混凝土橋面板厚度由160 mm提升至220 mm,組合梁極限承載力提升了20.4%。
3) 栓釘直徑由13 mm提升至22 mm時,組合梁極限承載力提升了29%,研究結果表明增加栓釘直徑能夠有效提高組合梁的極限承載力。

