標(biāo)注Petri 網(wǎng)中的最小初始標(biāo)識(shí)估計(jì)
徐淑琳,周廣瑞,岳 昊,2
(1.青島大學(xué)自動(dòng)化學(xué)院,山東青島 266071;2.青島大學(xué)復(fù)雜性科學(xué)研究所,山東青島 266071)
0 概述
Petri 網(wǎng)是一種用于離散事件系統(tǒng)建模、分析和控制的工具,具有圖形和數(shù)學(xué)的雙重表現(xiàn)形式且可有效描述系統(tǒng)行為。近年來,Petri 網(wǎng)被應(yīng)用于交通系統(tǒng)[1]和柔性裝配制造系統(tǒng)[2]等多種實(shí)際系統(tǒng)中,且在系統(tǒng)安全及可靠性分析[3-4]、業(yè)務(wù)流程分析[5-6]、交互控制[7]以及Web 服務(wù)分析和替代[8]中也有廣泛應(yīng)用。隨著實(shí)際系統(tǒng)規(guī)模的增大,標(biāo)識(shí)估計(jì)對(duì)離散事件系統(tǒng)的診斷[9]和控制器設(shè)計(jì)[10-11]等具有重要的作用。
關(guān)于Petri 網(wǎng)中標(biāo)識(shí)估計(jì)問題的研究已經(jīng)取得顯著成果[12-13]。文獻(xiàn)[12]基于對(duì)標(biāo)注序列的觀察,討論了初始標(biāo)識(shí)已知的Petri 網(wǎng)中的標(biāo)識(shí)估計(jì)問題,并指出標(biāo)識(shí)集可用一組具有固定結(jié)構(gòu)的線性不等式來描述。文獻(xiàn)[13]也研究了標(biāo)識(shí)估計(jì)問題,并證明所有可能的標(biāo)識(shí)數(shù)目是關(guān)于k的函數(shù)。最小初始標(biāo)識(shí)的估計(jì)成為當(dāng)今研究的熱點(diǎn)之一,例如文獻(xiàn)[14]討論了含有可觀測(cè)變遷的標(biāo)注Petri 網(wǎng)中的最小初始標(biāo)識(shí)估計(jì)問題,并提出一種最小初始標(biāo)識(shí)估計(jì)算法。文獻(xiàn)[15]將文獻(xiàn)[14]中的結(jié)果擴(kuò)展到含有不可觀測(cè)變遷的標(biāo)注Petri 網(wǎng)中。文獻(xiàn)[16]提出一種用于估計(jì)由標(biāo)注Petri 網(wǎng)中的最小代價(jià)計(jì)劃序列的算法。文獻(xiàn)[17]通過使用基可達(dá)圖尋找標(biāo)注Petri 網(wǎng)中最小代價(jià)變遷序列。
針對(duì)不可觀測(cè)變遷的存在給求解標(biāo)注Petri 網(wǎng)建模制造系統(tǒng)中的最小資源帶來困難的問題,本文放寬對(duì)不可觀測(cè)變遷發(fā)生個(gè)數(shù)的限制,且允許可觀測(cè)在變遷前至多有2 個(gè)不可觀測(cè)變遷發(fā)生。為了更好地實(shí)現(xiàn)估計(jì)最小初始標(biāo)識(shí)的目標(biāo),本文以標(biāo)注Petri 網(wǎng)為工具,進(jìn)一步討論了文獻(xiàn)[14-15]提出的最小初始標(biāo)識(shí)估計(jì)問題,并提出一種基于動(dòng)態(tài)規(guī)劃的新算法,以估計(jì)最小的初始標(biāo)識(shí)。
1 基本概念
本節(jié)給出下文將會(huì)用到的Petri 網(wǎng)和標(biāo)注Petri網(wǎng)的相關(guān)定義,更多詳細(xì)介紹可參閱文獻(xiàn)[14]。
定義1[18-19]將一個(gè)Petri 網(wǎng)定義為一個(gè)四元組N=(P,T,F(xiàn),W),其中:1)P={p1,p2,…,pn}是一個(gè)有限的庫(kù)所集,庫(kù)所使用空心圓圈表示;2)T={t1,t2,…,tm}是一個(gè)有限的變遷集,變遷使用實(shí)心豎條表示;3)P∪T≠?,P∩T=?;4)F?(P×T)∪(T×P)為流關(guān)系集合;5)W:F→?={0,1,2,…}稱為權(quán)函數(shù)。
如果pi和tj之間沒有弧,則W(pi,tj)=W(tj,pi)=0。如果N沒有直接的循環(huán)存在,則稱N是無環(huán)的。
定義2[17]在一個(gè)Petri 網(wǎng)N=(P,T,F(xiàn),W)中,若P={p1,p2,…,pn},T={t1,t2,…,tm},則N的結(jié)構(gòu)可用關(guān)聯(lián)矩陣A表示,其中:1)A=A+?A?;2)A?為N的輸入關(guān)聯(lián)矩陣,A?=[]是一個(gè)n行m列的整數(shù)矩陣,=W(pi,t)j(1≤i≤n,1≤j≤m);3)A+為N的輸出關(guān)聯(lián)矩陣,A+=[]是一個(gè)n行m列的整數(shù)矩陣,=W(tj,pi);4)若pi和tj之間沒有弧,則==0;5)A(:,t)(或者A?(:,t),A+(:,t))是A(或者A?,A+)中對(duì)應(yīng)于變遷t的列,且A(:,t),A?(:,t),A+(:,t)均為列向量。
定義3(N,Μ0)是一個(gè)初始化的網(wǎng)系統(tǒng),Μ0是系統(tǒng)的初始標(biāo)識(shí)。映射Μ:P→? 稱為Petri 網(wǎng)N的一個(gè)標(biāo)識(shí),標(biāo)識(shí)Μ的每個(gè)分量都對(duì)應(yīng)相應(yīng)庫(kù)所中托肯的數(shù)目,托肯用實(shí)心圓點(diǎn)表示。對(duì)于p∈P,庫(kù)所p中的托肯數(shù)記為Μ(p),標(biāo)識(shí)Μ的所有庫(kù)所中的托肯總數(shù)記為。
定義4[14]Petri 網(wǎng)N=(P,T,F(xiàn),W)具有以下變遷發(fā)生規(guī)則:
1)對(duì)于變遷t∈T,如果t的每個(gè)輸入庫(kù)所pinput都有至少A?(pinput,t)個(gè)托肯,則變遷t在標(biāo)識(shí)Μ下具有發(fā)生權(quán),并定義為Μ[t〉。
2)如果變遷t發(fā)生,則t的每個(gè)輸入庫(kù)所pinput都被移除A?(pinput,t)個(gè)托肯,并且t的每個(gè)輸出庫(kù)所poutput都增加A+(poutput,t)個(gè)托肯,變遷t在標(biāo)識(shí)Μ下發(fā)生會(huì)使得系統(tǒng)到達(dá)一個(gè)新標(biāo)識(shí)Μ?=Μ+A(:,t),并記為Μ[t〉Μ?。
定義5[20]Petri 網(wǎng)N=(P,T,F(xiàn),W)的可達(dá)性可定義為:若存在t∈T使得Μ[t〉Μ?,則稱標(biāo)識(shí)Μ?從Μ直接可達(dá);若存在一個(gè)變遷序列σ=t1t2…tk,其中ti∈T,使得Μ[t1〉Μ1[t2〉…Μk?1[tk〉Μk=Μ?,則稱標(biāo)識(shí)Μ?從Μ可達(dá)。按此規(guī)定,從Μ可達(dá)的一切標(biāo)識(shí)集合記為R(Μ)。
定義6給定一個(gè)變遷序列σ∈T*,其中T*表示一系列有限長(zhǎng)度的變遷序列集合。令π:T*→?n為一個(gè)映射,y=π(σ)是一個(gè)m維非負(fù)向量,稱為σ的發(fā)生數(shù)向量。y(i)表示變遷序列σ中變遷t出現(xiàn)的次數(shù)。對(duì)于零長(zhǎng)度的空串?∈T*,其發(fā)生數(shù)向量為零向量,即π(?)=0m。
定義7[17]將一個(gè)標(biāo)注Petri 網(wǎng)定義為一個(gè)四元組(N,Μ0,L∪{?},l),其中:1)N=(P,T,A,W)是一個(gè)Petri 網(wǎng),Μ0是Petri 網(wǎng)N的初始標(biāo)識(shí);2)L是非空標(biāo)注的集合,標(biāo)注用一個(gè)字母表示;3)l:T→L∪{?}是標(biāo)注函數(shù),其中每個(gè)變遷都對(duì)應(yīng)一個(gè)字母或者一個(gè)空字符串∫。
由于本文考慮的是含有不可觀測(cè)變遷的標(biāo)注Petri網(wǎng),因此可以將變遷集合T劃分為所有不可觀測(cè)變遷的集合Tu和所有可觀測(cè)變遷的集合To這2 個(gè)集合,且滿足Tu∪To=T和Tu∩To=?。對(duì)于一個(gè)標(biāo)注l∈L,用Tl={t∈T|l(t)=l}表示與非空標(biāo)注l對(duì)應(yīng)的所有可觀測(cè)變遷的集合,Tu={t∈T|l(t)=?}表示與空標(biāo)注?對(duì)應(yīng)的所有不可觀測(cè)變遷的集合,用|Tl|(或者|Tu|)表示對(duì)應(yīng)于非空標(biāo)注l(或者空標(biāo)注?)的變遷數(shù)目,且滿足1≤|Tl|≤m,1≤|Tu|≤m。對(duì)于一個(gè)變遷序列σ=t1t2…tk,其對(duì)應(yīng)的標(biāo)注序列可定義為w=(σ)≡l(t1)l(t2)…l(tk)。
2 最小初始標(biāo)識(shí)的求取
2.1 問題描述
文獻(xiàn)[14]考慮的是僅含有可觀測(cè)變遷的標(biāo)注Petri 網(wǎng),而本文的研究對(duì)象是含有不可觀測(cè)變遷的標(biāo)注Petri 網(wǎng),在觀察到一個(gè)標(biāo)注后,所有可能的變遷發(fā)生序列的數(shù)目會(huì)呈指數(shù)級(jí)增長(zhǎng)。因此,為了降低計(jì)算復(fù)雜度,本文進(jìn)行以下假設(shè):
假設(shè)1不可觀測(cè)變遷組成的子網(wǎng)是無環(huán)的。
根據(jù)假設(shè)1,在標(biāo)注Petri 網(wǎng)N中,不可觀測(cè)變遷組成的子網(wǎng)沒有直接的循環(huán)存在。
假設(shè)2對(duì)于每個(gè)標(biāo)注的觀察,可觀測(cè)變遷之前至多允許2 個(gè)不可觀測(cè)變遷發(fā)生。
根據(jù)假設(shè)2,在觀察到標(biāo)注lj后,所有可能的變遷發(fā)生序列形如σu t,其中t∈To,l(t)=lj,σu∈T*u,σu可能為一個(gè)空串?。
考慮一個(gè)含有不可觀測(cè)變遷且初始標(biāo)識(shí)未知的標(biāo)注Petri 網(wǎng)N=(N,Μ0,L∪{?},l)以及一個(gè)標(biāo)注序列w=l1l2…lk,其中l(wèi)j∈L,j∈{1,2,…,k},本文的目標(biāo)為尋找最小初始標(biāo)識(shí)估計(jì),即具有最小托肯總數(shù)的標(biāo)識(shí)估計(jì)。
定義8[15]考慮一個(gè)標(biāo)注Petri 網(wǎng)N=(N,Μ0,L∪{?},l),給定一個(gè)標(biāo)注序列w,將初始標(biāo)識(shí)估計(jì)集合、極小初始標(biāo)識(shí)估計(jì)集合、最小初始標(biāo)識(shí)估計(jì)集合分別定義為:

假設(shè)Μ和Μ?是2 個(gè)分量個(gè)數(shù)相同的標(biāo)識(shí)向量,其中Μ=[Μ(p1),Μ(p2),…,Μ(pn)]T,Μ?=[Μ ?(p1),Μ ?(p2),…,Μ ?(pn)]T,如果對(duì)任意的i∈{1,2,…,n}滿足Μ(pi)≤Μ ?(pi),則有Μ≤Μ?成立。假設(shè)一個(gè)標(biāo)識(shí)集合Z={Μ1,Μ2,…,Μn},若對(duì)任意的i,j∈{1,2,3,…}且i≠j,都不存在Μj使得Μj≤Μi成立,則Μi為標(biāo)識(shí)集合Z中的極小標(biāo)識(shí)。由于小于等于關(guān)系是一種偏序關(guān)系,因此極小標(biāo)識(shí)并不是唯一的。
在文獻(xiàn)[15]中,式(4)給出了極小初始標(biāo)識(shí)的計(jì)算方法:


圖1 節(jié)點(diǎn)演化示意圖Fig.1 Schematic diagram of nodes evolution
圖2所示為一個(gè)標(biāo)注Petri網(wǎng)(N,Μ0,L∪{?},l),P={p1,p2,p3},T={t1,t2,t3,t4},其中To={t1,t4},Tu={t2,t3},(lt1)=a,(lt4)=b,(lt2)=(lt3)=?。給定一個(gè)標(biāo)注序列w=ab,對(duì)w進(jìn)行觀察后,利用式(4)計(jì)算極小初始標(biāo)識(shí)估計(jì),得到節(jié)點(diǎn)演化示意圖如圖3 所示,節(jié)點(diǎn)信息如表1 所示。觀察到標(biāo)注序列ab后,當(dāng)變遷序列t1t2t3t4發(fā)生時(shí),得到極小初始標(biāo)識(shí)估計(jì)集合為(w)={[0000]T},最小初始標(biāo)識(shí)估計(jì)集合為I(w)={[0000]T},I(w)對(duì)應(yīng)的變遷序列集合為{t1t2t3t4},I(w)對(duì)應(yīng)的發(fā)生數(shù)向量集合為{[1111]T}。
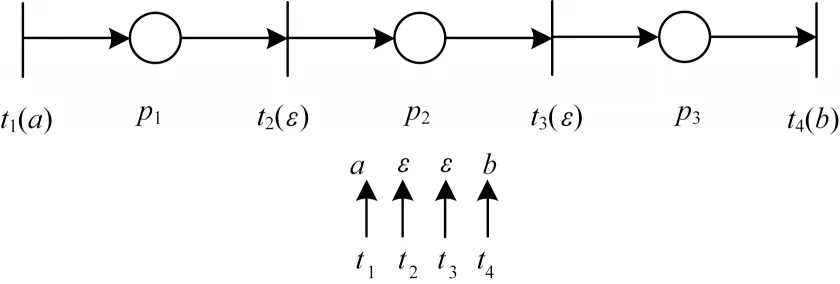
圖2 標(biāo)注Petri 網(wǎng)示意圖Fig.2 Schematic diagram of labeled Petri nets
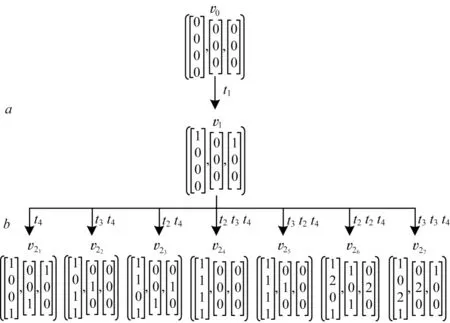
圖3 Petri 網(wǎng)的節(jié)點(diǎn)演化示意圖Fig.3 Schematic diagram of node evolution of Petri nets
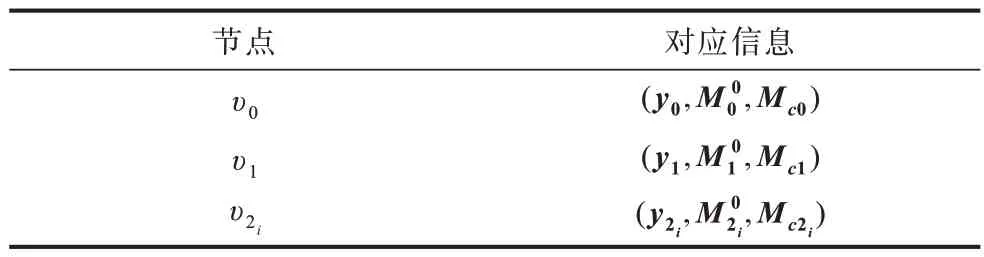
表1 圖3 中每個(gè)節(jié)點(diǎn)對(duì)應(yīng)的信息Table 1 Corresponding information of each node in Fig.3
2.2 最小初始標(biāo)識(shí)算法估計(jì)

算法1最小初始標(biāo)識(shí)估計(jì)算法


2.3 復(fù)雜性分析
由文獻(xiàn)[14]可知,第j階段的發(fā)生數(shù)向量的數(shù)目為nj=O(jb),b是一個(gè)依賴于Petri 網(wǎng)結(jié)構(gòu)的參數(shù)。給定一個(gè)含有n個(gè)庫(kù)所、m個(gè)變遷的標(biāo)注Petri 網(wǎng),其中可觀測(cè)變遷和不可觀測(cè)變遷的個(gè)數(shù)分別為mo和mu,且有m=mo+mu成立。在觀察到一個(gè)標(biāo)注后,所有可能不同的不可觀測(cè)發(fā)生數(shù)向量的數(shù)目為:
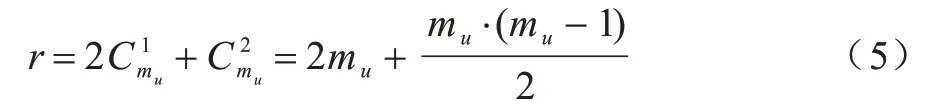
綜合考慮可觀測(cè)變遷和不可觀測(cè)變遷,基于假設(shè)2,可知第j階段發(fā)生數(shù)向量的數(shù)目為nj=(r?j)b。在第j?1 階段,一個(gè)發(fā)生數(shù)向量至多能產(chǎn)生r?m0個(gè)不同的發(fā)生數(shù)向量,因此第j階段新產(chǎn)生的發(fā)生數(shù)向量的總數(shù)為r?m0?nj?1=O[r?m0?(r?j)b]。在Petri 網(wǎng)中僅含有可觀測(cè)變遷的情況下,第j階段極小初始標(biāo)識(shí)的數(shù)目為qj=O(jn),根據(jù)假設(shè)2,發(fā)生序列長(zhǎng)度的最大值為3j,因此qj=O((3j)n)=O(jn)。針對(duì)每個(gè)發(fā)生數(shù)向量,需要進(jìn)行nj次比較以確定其是否已經(jīng)出現(xiàn)在節(jié)點(diǎn)Rj中,若已出現(xiàn)過,則需要qj次比較來確定極小的初始標(biāo)識(shí)估計(jì)。基于以上分析,算法1 的計(jì)算復(fù)雜度為:
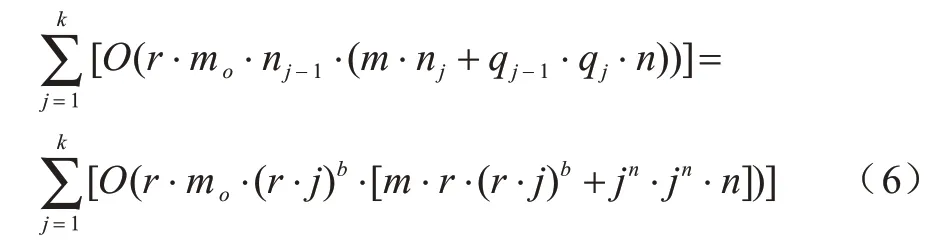
式(6)可簡(jiǎn)化為:
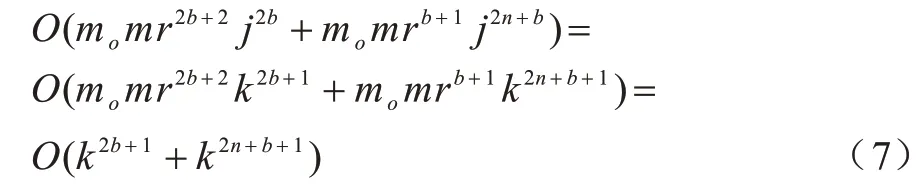
因此,算法1 的計(jì)算復(fù)雜度是關(guān)于k的多項(xiàng)式。
3 應(yīng)用實(shí)例
本節(jié)通過一個(gè)實(shí)例來驗(yàn)證算法1 的有效性,并將運(yùn)行結(jié)果與現(xiàn)有算法得到的結(jié)果進(jìn)行對(duì)比分析。圖4給出了一個(gè)2臺(tái)并行機(jī)器的標(biāo)注Petri網(wǎng)模型N=(N,Μ0,L∪{?},l),庫(kù)所集P={p1,p2,p3,p4},變遷集T={t1,t2,t3,t4,t5,t6},其中To={t1,t2,t5,t6},Tu={t3,t4},l(t1)=a,l(t2)=b,l(t5)=c,l(t6)=d,l(t3)=l(t4)=?。p1為存放工件的資源庫(kù)所,變遷t1和t2表示由機(jī)器人分別將工件裝載至1 號(hào)機(jī)器和2 號(hào)機(jī)器上,p2表示工件被1 號(hào)機(jī)器加工,t3表示機(jī)器人將一部分工件從1 號(hào)機(jī)器上卸載并裝載至2 號(hào)機(jī)器上,p3表示工件被2 號(hào)機(jī)器加工,t5表示機(jī)器人將剩余的工件從1 號(hào)機(jī)器上卸載,t4表示機(jī)器人將工件從2 號(hào)機(jī)器上卸載,p4表示將來自1 號(hào)機(jī)器和2 號(hào)機(jī)器的工件進(jìn)行再加工,t6表示將工件卸載。給定一個(gè)標(biāo)注序列w=ad,運(yùn)行算法1 后得到節(jié)點(diǎn)演化示意過程如圖5 所示,節(jié)點(diǎn)信息和弧上的標(biāo)記信息分別如表2和表3所示。如圖5 所示,當(dāng)觀察到標(biāo)注a時(shí),所有可能的變遷序列集合為{t1,t3t1,t4t1,t3t4t1,t4t3t1,t3t3t1,t4t4t1},應(yīng)該存在7個(gè)節(jié)點(diǎn),但變遷序列t3t4t1和t4t3t1對(duì)應(yīng)的發(fā)生數(shù)向量均為[101100]T,兩者對(duì)應(yīng)的極小初始標(biāo)識(shí)估計(jì)分別為[1100]T和[1110]T,顯然[1100]T≤[1110]T,根據(jù)算法1,當(dāng)出現(xiàn)相同的發(fā)生數(shù)向量時(shí),僅保留極小初始標(biāo)識(shí)估計(jì),因此刪掉變遷序列t4t3t1對(duì)應(yīng)的初始標(biāo)識(shí)估計(jì)及當(dāng)前標(biāo)識(shí)。當(dāng)標(biāo)注序列w=ad全部被觀察到后,得到極小初始標(biāo)識(shí)估計(jì)集合為(w)={[1000]T},最小初始標(biāo)識(shí)估計(jì)集合為Ι(w)={[1000]T},與Ι(w)對(duì)應(yīng)的變遷序列集合為{t1t3t4t6},與Ι(w)對(duì)應(yīng)的發(fā)生數(shù)向量集合為{[101101]T}。

圖4 標(biāo)注Petri 網(wǎng)系統(tǒng)示意圖Fig.4 Schematic diagram of labeled Petri net system
文獻(xiàn)[15]中限定可觀測(cè)變遷發(fā)生之前至多允許一個(gè)不可觀測(cè)變遷發(fā)生,則最小初始標(biāo)識(shí)估計(jì)集合為Ι?(w)={[1001]T},發(fā)生數(shù)向量集合為{[100001]T,[101001]T},變遷序列為{t1t6,t1t3t6}。假設(shè)Μ∈Ι(w),Μ?∈Ι?(w),則||Μ||=1,||Μ?||=2,由此可知||Μ||<||Μ?||,因此,應(yīng)用本文方法得到的最小初始標(biāo)識(shí)具有更小的托肯總數(shù),即系統(tǒng)完成指定的任務(wù)序列所需的初始資源更少。
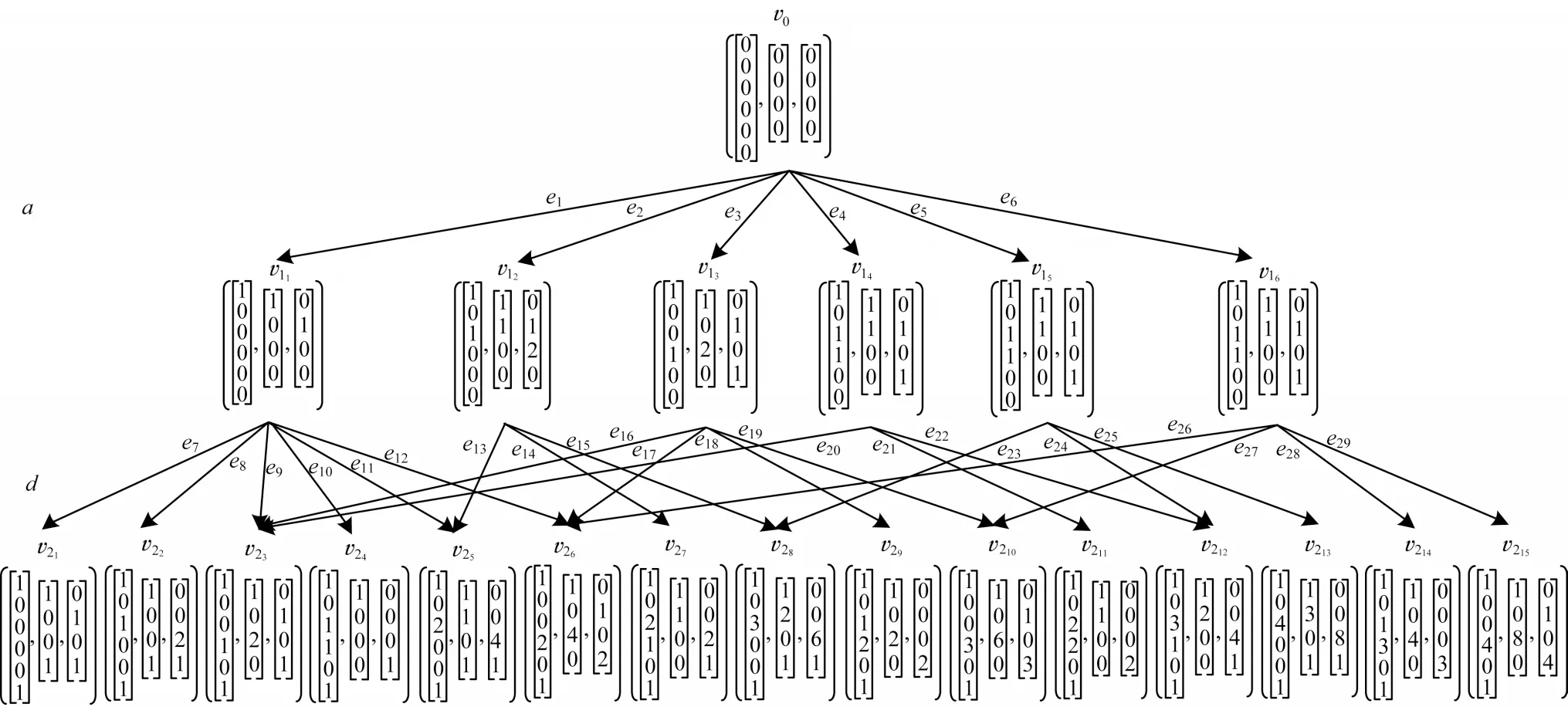
圖5 運(yùn)行算法1 后的節(jié)點(diǎn)演化示意圖Fig.5 Schematic diagram of node evolution after running algorithm 1

表2 圖5 中每個(gè)節(jié)點(diǎn)對(duì)應(yīng)的信息Table 2 Corresponding information of each node in Fig.5
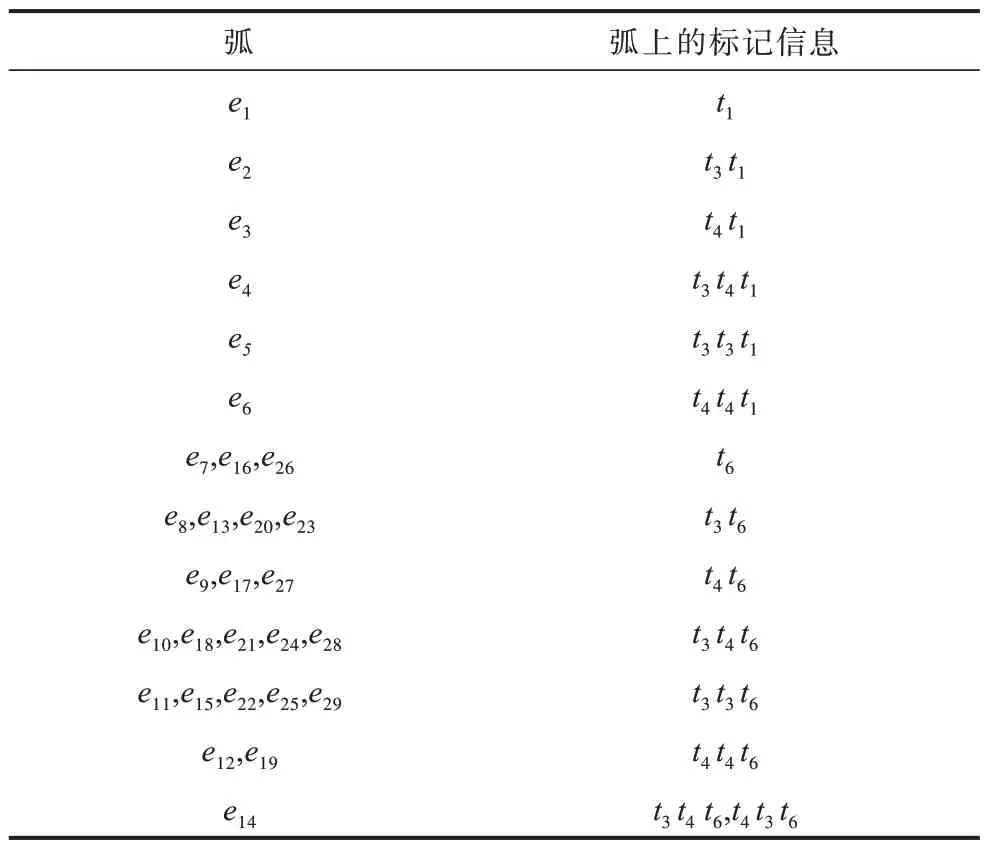
表3 圖5 中每條弧上的標(biāo)記信息Table 3 Marking information of each arc in Fig.5
4 結(jié)束語(yǔ)
針對(duì)制造系統(tǒng)中的最小資源問題,本文建立標(biāo)注Petri 網(wǎng)模型,并提出一種用于估計(jì)最小初始標(biāo)識(shí)的算法。該算法放寬了不可觀測(cè)變遷發(fā)生個(gè)數(shù)的限制,并規(guī)定可觀測(cè)變遷之前至多允許2 個(gè)不可觀測(cè)變遷發(fā)生,以有效避免最小初始標(biāo)識(shí)估計(jì)的窮舉計(jì)算。實(shí)驗(yàn)結(jié)果表明,在含有不可觀測(cè)變遷的標(biāo)注Petri 網(wǎng)中,應(yīng)用本文算法估計(jì)的最小初始標(biāo)識(shí)較現(xiàn)有算法得到的結(jié)果更優(yōu)。下一步將利用時(shí)延Petri 網(wǎng)結(jié)構(gòu)對(duì)本文算法進(jìn)行優(yōu)化,使得初始標(biāo)識(shí)估計(jì)的托肯總數(shù)更小。

