多特征融合的超像素譜聚類MRI腦腫瘤圖像分割

白志超，康維新

哈爾濱工程大學 信息與通信工程學院，黑龍江 哈爾濱 150001

核磁共振成像(magnetic resonance imaging,MRI)為腦腫瘤的診斷與規劃治療提供了豐富的信息，但是由于腦腫瘤的大小、形狀和強度都各不相同，使得腫瘤分割變得困難。同時由于成像技術的原因，MRI圖像也受到強度不均勻的影響，也會影響分割的準確性。在臨床中，腦腫瘤的分割都是靠人工標注的，這是非常耗時的，并且也依賴于醫生的經驗，因此腦腫瘤的自動分割也成為醫學領域一項具有挑戰性的難題。

無監督聚類與有監督聚類相比不需要大量的標記數據集，可以在不損失分割精度的前提下降低計算復雜度、提高計算效率。用于腦腫瘤圖像分割的無監督方法包括Fuzzy-c-Means(FCM)[1]、Gaussian Mixture Model(GMM)[2]、K-means[3-4]和Region Seeds Growing(RSG)[5]等。譜聚類是近些年比較流行的一種無監督聚類方法，它是一種基于圖的聚類方法[6]，與其他聚類技術相比可以在多項式時間內產生全局最優解。但是譜聚類依賴圖節點之間構造的相似矩陣，當數據量大的時候，會帶來計算復雜度較高的問題。為了克服譜聚類的缺點，Fowlkes[7]采用Nystrom方法，可以用少量的采樣像素來逼近相似度矩陣，提高了計算效率，然而由于數據量大、特征向量之間不正交等原因，影響了分割結果的準確性。超像素最開始由Ren等[8]提出，它代表了一個連貫的局部區域，保留了圖像的大部分特征，利用超像素可以顯著地降低圖的節點數，加快圖的劃分。文獻[9]首先使用K-means生成超像素，然后通過譜聚類對超像素進行聚類，進而完成了對腦腫瘤的分割。

本文基于譜聚類和超像素在圖像分割中的成功應用，提出了多特征融合的超像素譜聚類MRI腦腫瘤圖像分割方法。采用超像素為圖節點，構建了一種融合圖像空間、顏色和紋理特征的相似度計算函數，進而求得歸一化拉普拉斯矩陣，然后對其特征向量進行聚類來完成對圖像的分割。通過實驗結果表明，該方法有效地降低了計算復雜度，提高了分割精度。

1 相關基礎概念

1.1 SLIC算法

SLIC算法是近些年比較流行的超像素分割算法[10]，其根據空間距離和顏色相似特征進行局部的迭代聚類。SLIC方法是K-means聚類在生成超像素時的一種改進，與K-means相比它有兩個重要的改進：1)SLIC將聚類搜索空間限制為與超像素的大小成比例，這樣可以將K-means算法的復雜度降為常數，整個算法復雜度為線性。2)同時考慮顏色和空間距離并且進行加權處理，可以對超像素的邊界依附性和緊湊型加以控制，它有一個參數K，可以控制超像素的數量。SLIC算法簡單易于理解，通過不斷地進行迭代聚類，直到結果收斂。通過限制聚類的搜索區域，顯著地降低了計算復雜度，生成的超像素具有規則的尺寸。SLIC的距離計算公式為

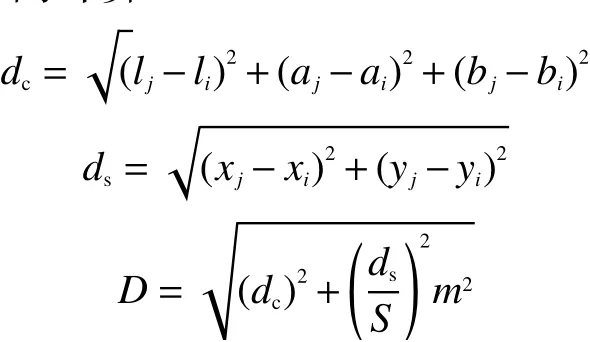
式中：ds為空間距離；dc為顏色距離；S為網格間隔；m為權衡因子，l、a、b分別為Lab顏色空間各通道的值，x、y為像素點坐標。m大時，空間鄰近性更重要；m小時，顏色相似性更重要。

1.2 譜聚類算法

譜聚類是一種目前比較流行的基于圖的無監督聚類技術[6]。它將需要聚類的數據看作為空間中的點，然后通過邊將這些點連接起來，并賦予各個邊權重值。將間隔較遠的兩點之間的邊賦予較低權重，而相距較近的兩點之間的邊賦予較高權重，通過對聚類數據點構成的圖進行切圖，讓切圖后不同聚類間邊權重和盡可能低，而同一聚類內的邊權重和盡可能高，以達到對數據聚類的目的。NJW是一種經典的譜聚類方法[11]，其通過對拉普拉斯矩陣的特征向量和特征值進行分解來對數據進行聚類。給定一個圖像I={I1,I2,···,In}，其中I1,I2,···,In表示圖像中的像素，將圖像表示成一個加權無向圖G={V,E}， 其中V表示圖中的節點，E表示節點之間的邊，在計算相似度矩陣時，第i個節點和第j個節點之間的相似度量函數可以表示為

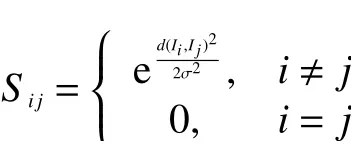
式中：d(Ii,Ij)表示節點Ii與節點Ij之間的歐氏距離；σ為高斯核尺度參數。然后將相似度矩陣轉化為歸一化拉普拉斯矩陣進行特征向量分解。最后，利用K-means算法對最小的k個特征值進行聚類，得到原始信息聚類結果。

2 多特征融合的超像素譜聚類腦腫瘤圖像分割

2.1 非局部均值濾波去噪

由于成像技術的原因，原始MRI圖像中會不可避免地帶有噪聲，并且噪聲通常服從Rician分布，非局部均值濾波(non-local means, NL-Means)技術被發現能很好地處理MRI圖像中的噪聲[12]，該算法利用圖像中普遍存在的冗余信息來去除噪聲，它利用整幅圖像來去噪，以圖像塊為單位在圖像中尋找相似區域，再對這些區域求平均，能夠比較好地去掉MRI圖像中的噪聲。NL-Means濾波過程可以表示為

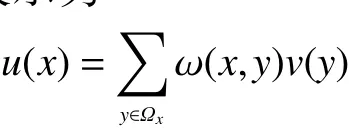
式中 ω(x,y)為 權重值，表示在原始圖像I中像素x和像素y之間的相似度。 ω(x,y)需要滿足式(1)表示的條件，圖1給出了去噪后的效果。

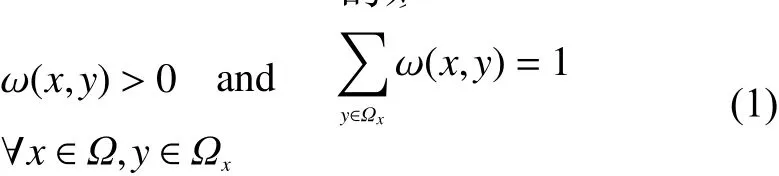
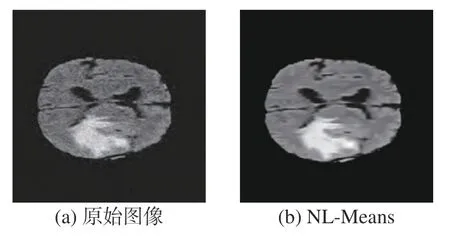
圖1 去噪后圖像

2.2 構建相似度度量函數

將去噪后的MRI圖像通過SLIC算法進行超像素分割，進而獲得構建加權無向圖的節點，SLIC分割結果如圖2。因為譜聚類具有對高斯核尺度參數σ的選取敏感的特點，并且MRI醫學圖像感興趣區域(ROI)總是存在邊界模糊的現象，單一的采用距離及顏色特征度量超像素節點之間的相似性并不會獲得良好的分割效果，因此本文構建了一種融合多特征的相似度度量函數，在距離及顏色特征的基礎上添加MRI圖像的紋理特征，并且采用自適應的方式計算尺度參數σ。

圖2 超像素分割

2.2.1 獲取紋理體征

局部二值模式(local binary pattern, LBP)是一種常用來描述圖像紋理特征的算子，它具有旋轉不變性和灰度不變性等優點。其定義在一個3×3的窗口內，以窗口中心的像素作為閾值，并將其與其8鄰域內的像素的灰度值進行比較，進而得到該區域的紋理信息[13]，如圖3所示，用公式表示為

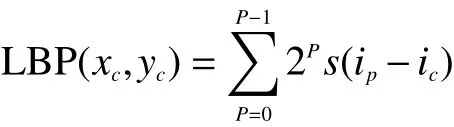
式中： (xc,yc)為 中心像素；ic為 中心像素灰度值；in為相鄰像素的灰度值；s(x)是一個符號函數。

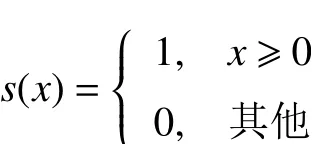
圖3 紋理特征

2.2.2 構建相似度矩陣

給定N個超像素，加權無向圖被表示成一個N×N的相似度矩陣，第i個 超像素與第j個超像素之間的相似距離定義為

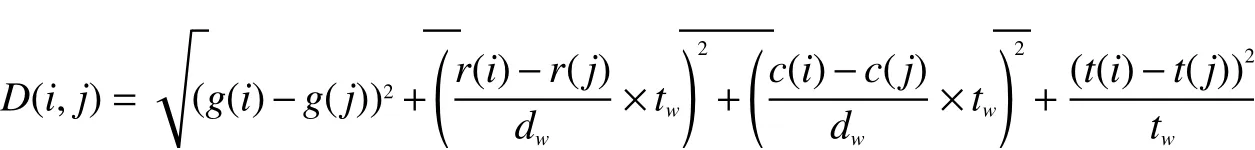
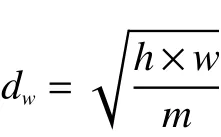
式中：g(i)、r(i) 和c(i)分別表示超像素的平均灰度值和平均位置；t(i)為超像素的平均紋理特征值，同時由于空間距離依賴于圖像的大小，因此添加空間加權因子dw；其中h為 圖像高度；w為圖像寬度，在實驗中，將m設 置為固定值100；tw為紋理特征調節參數，在實驗中設置為固定值10。

計算相似距離之后，選擇fully connected graph的方式構建相似度矩陣，相似度矩陣S定義如下：

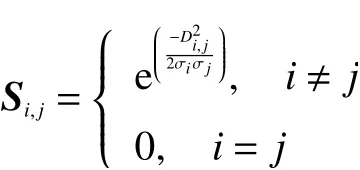
其中：

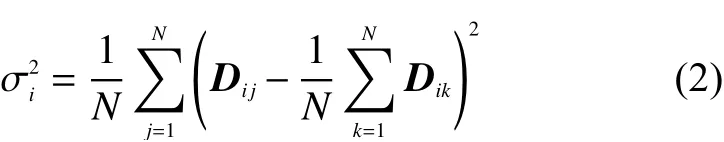
譜聚類算法相比于其他分割算法能更有效的進行聚類，但是它的計算復雜度為O(N3/2)，采用SLIC進行超像素分割可以大大降低N，提高計算效率。同時本文構造的相似度矩陣融合了MRI圖像的紋理信息，可以更好反應圖像的結構與信息，采用式(4)計算σ可以有效地避免人為選取σ帶來的敏感性問題。

3 對比試驗與結果分析

為了驗證本文方法，分別與INJW算法[14]和RSF-Ncut算法[15]進行對比分割實驗。實驗所用的數據來自BraTS 2015數據集[2]，實驗機器采用PC機，Inter Core i5 2.6 GHZ處理器，8 GB內存，實驗平臺為MATLAB 2019b，圖4給出了以上3種分割方法與人工分割的對比圖。

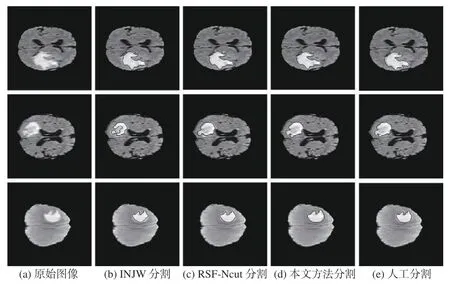
圖4 3種算法分割結果及人工分割的對比圖

為了定量評估算法的性能，本文選用相似性系數(Dice)、相對體積誤差(RVD)和靈敏度(Sensitivity)作為腦腫瘤分割結果的評價指標，其中Dice表示分割結果和groundtruth之間的重疊程度，RVD表示分割結果和groundtruth之間體積的差值，Sensitivity表示正確分割的腫瘤占真值腫瘤的比例，實驗中對每幅圖像均做了多次實驗，結果取平均值。

式中Rseg和Rgt分別表示算法分割結果和人工分割。

從視覺效果來看，本文方法較對比方法更能保持分割出的腦腫瘤部位的完整性，在邊界保持上也具有更好的效果。表1給出本文方法與INJW方法和RSF-Ncut方法的分割性能對比，可以看出，在所選取的3個性能指標上，本文方法均高于對比算法。因此，本文方法具有更高的分割精度和更優的分割效果。

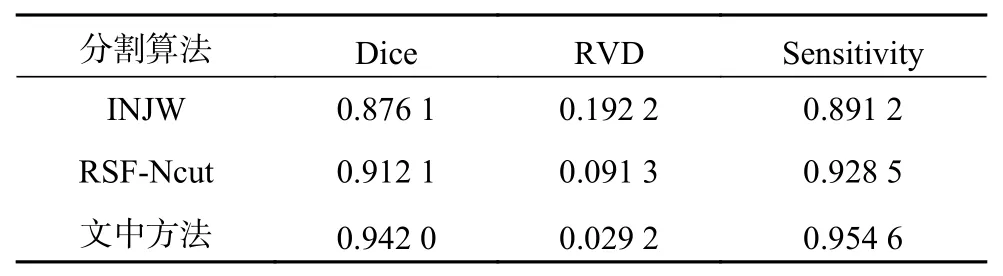
表1 3種分割方法性能對比

4 結論

本文提出了一種多特征融合的超像素譜聚類MRI腦腫瘤圖像分割方法，算法有以下特點：

1)采用超像素代替單一像素為圖節點構建加權無向圖，有效地降低了譜聚類的計算復雜度，提高了計算效率。

2)在計算相似度矩陣時，融合多種圖像特征，使相似度矩陣更全面地反映了圖像的信息。實驗表明，本文所提方法在Dice、RVD和Sensitivity3個性能評價指標上均優于對比方法，達到了更高的分割精度，具有實際應用價值。

本文的算法也存在局限性，還有很大的提升空間，具體表現在：在計算相似度矩陣時存在大量的指數運算，比較耗時，因此分割實時性還有待提高。未來將對算法的分割實時性作進一步的探索，尋找更加快速有效的方法。